尾缘控制措施对开式空腔噪声抑制效果研究

张群峰， 闫盼盼， 黎军

(1.北京交通大学 土木工程学院， 北京 100044; 2.中国航空工业集团有限公司 沈阳飞机设计研究所， 辽宁 沈阳 110035)

0 引言

空腔结构被广泛应用于航空航天及其他工业领域，如起落架舱、武器舱、敞篷汽车等。虽然空腔构型十分简单，但却包含着极其复杂的流动物理现象，包括剪切层失稳、旋涡生成与发展、涡/声干扰，特别是超声速条件下，还存在激波与剪切层、波/涡/剪切层相互干扰等。这使得腔体内部产生强烈的压力脉动，并伴随着刺耳的噪声，引起腔体内设备产生疲劳破坏。因此自上世纪50年代以来空腔流动问题引起了众多研究者的关注。Krishnamurthy[1]、Charwat[2]、Rossiter[3]、Heller等[4]、Covert等[5]最早通过风洞实验研究了空腔流动问题，并根据空腔长深比及其流动特性提出了3种主要流态：开式流动(L/D<10)、过渡式流动(1013)，L为空腔长度，D为空腔深度。Rossiter[3]于1964年提出了被广泛接受的开式空腔自持振荡理论，认为开式空腔噪声产生主要存在以下4个关键环节：1)剪切层由于自身不稳定性或受扰动形成脱落涡；2)脱落涡向后传播并与腔体后壁碰撞，产生强烈的噪声；3)声波通过空腔内部向上游传递；4)回流或前传声波扰动剪切层失稳并形成新的脱落涡。在满足一定的空气动力条件和相位条件时，腔内流动形成自持振荡，腔内产生远高于宽频噪声的腔体纯音噪声，出现多个声压级峰值的激振频率。

对空腔发声机理进行研究的最终目的是希望能够对空腔流动进行有效地控制来降低腔内噪声水平。针对噪声控制方法可以分为主动控制和被动控制两种，国内外学者对于两种控制方法都已进行了多种尝试。被动控制方面：黎军等[6-7]、Givogue等[8]、Thiemann等[9]通过风洞实验及数值模拟方法研究了前方加水平或竖直扰流杆对空腔噪声的抑制效果，发现扰流杆的分布形式及其形状是影响噪声抑制水平的重要因素；刘瑜等[10]、余培汛等[11]通过数值模拟方法研究发现空腔前方加锯齿形扰流板对腔内主导模态的降噪幅度在10 dB以上，空腔内部整体声压级降幅在5 dB左右；吴继飞等[12]通过高速风洞实验研究发现采用空腔前方加细悬金属丝的方法能有效降低腔底各测点的声压级；陶洋等[13]通过风洞实验研究发现在亚、跨声速条件下，采用前缘斜劈对空腔内噪声有较好的抑制效果，空腔后部区域声压级降低幅度比前部区域大。主动控制方面：Williams等[14]、杨党国等[15]、余培汛等[16]通过风洞实验及数值模拟方法研究了前缘射流对空腔纯音噪声的抑制效果，发现空腔噪声降低幅度与射流方向、射流质量、射流温度等均有较密切的关系；Zhang等[17]、王一丁等[18]通过风洞实验和数值模拟方法研究发现气帘吹流同样能起到抑制腔内压力脉动的作用；宁方立等[19]通过数值方法研究发现采用空腔前方平板高频振动的方法可以有效地改善空腔内部气动声学环境。

从上述文献可以看出，在研究方法方面，早期的研究更加偏向于以风洞实验为主，随着计算机性能的大幅度提升和一些新的湍流模型的提出，数值模拟的计算速度和计算精度都得到了极大的提升，数值模拟研究所占的比例逐步增加。同时数值模拟能够提供更加丰富的流场信息，有利于对空腔噪声控制的内在机理进行深入分析。在控制措施方面，现有研究大多是在腔体前缘施加控制来增强剪切层稳定性或改变剪切层形态，从而达到降低气动噪声的目的。从噪声产生机理可以看出，自持振荡环节的任何一环被打破都可以减弱噪声水平。因此本文选择在腔体尾部采用后壁开孔板加耗能腔的被动控制措施，来减弱剪切层与尾缘撞击产生的噪声幅值，并削弱前传声波及回流对前缘剪切层的扰动，从而控制开式空腔内噪声水平。采用基于Menter SST 湍流模型的改进延迟分离涡模拟(IDDES)方法，对不同控制措施对空腔噪声的抑制效果及其内在机理进行深入地研究。

1 数值计算方法

1.1 控制方程

本文主要研究高亚声速及超声速条件下腔体流动，考虑黏性影响，三维可压缩非定常的守恒型控制方程[20]表示为

(1)

式中：W为守恒变量；Fc为对流矢通量；Fv为黏性矢通量；Q为源项；Ω为控制体；dS为面元。

Navier-Stokes方程的求解采用有限体积法，对流通量采用2阶精度Roe格式，选用修正的Venkatakrishnan[21]限制器保证2阶精度插值且具有全变差递减(TVD)性质，同时又具有较小的数值耗散，扩散通量采用中心差分格式求解。时间离散采用的是2阶精度的双时间步格式进行非定常计算。

1.2 SST IDDES方法

湍流模拟采用基于SSTk-ω模型的IDDES方法[22]。该方法求解的k和ω方程与SSTk-ω模型方程形式相似，唯一不同的是IDDES模型的k方程中湍动能耗散项Dk计算方式发生了改变，其具体公式如下：

(2)

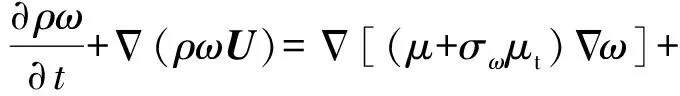
(3)

式中：ρ为密度；t为时间；U为速度向量；μ为分子黏性系数；μt为湍流黏性系数；Pk为湍动能生成项；ω为湍流耗散比；f1为经验混合函数；β=0.075；α=α1f1+α2(1-f1)，α1=5/9，α2=0.44；σk=0.85；σω=0.85；σω2=0.856；

(4)

lRANS为RANS模型长度尺度，lRANS=k1/2/Cμω，Cμ=0.09，lIDDES为亚格子长度尺度，lIDDES=min{max [cwdw,cwhmax,hwn],hmax}，hwn是垂直壁面方向的网格步长，dw为到壁面距离，cw为经验常数，cw=0.15，hmax为hwn的最大值，CDES为比例系数。

IDDES方法相比最初DES97[23]及DDES[24]方法，在保留了DES类方法优点的同时成功克服了对数律不匹配、网格诱导分离、模型应力损耗等问题[25]。

本文选取的数值方法已在前期发表的文献中得到了验证，其结果表明所采用的数值方法可以准确地求解空腔噪声问题，详见参考文献[26]。

1.3 数值纹影技术

通过实验方法获得的流动图像通常是纹影图，纹影图能直观地显示流场中波系、剪切层及涡团等流动现象。其原理为将流场中密度梯度的变化转变为记录平面上相对光强的变化，使可压缩流场中的激波、涡结构等密度变化剧烈的区域成为可观察、可分辨的图像。数值模拟方法能够获得全场的密度分布，因此通过对数值结果的处理可以得到类似的图像来展现流场结构，称为数值纹影。处理方法[26-27]如下：

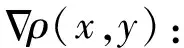
(5)

2)通过纹影函数定义特殊的非线性尺度Sch(x,y)：

Sch(x,y)=exp (-ckS(x,y)),

(6)

(7)

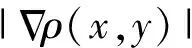
(8)

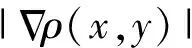
(9)

式中：c0、c1和ck为常数，c0=0.002,c1=0.03,ck=0.5.

3)将纹影函数值用灰度云图表示。

2 计算模型和网格划分

2.1 计算模型

本文选取的基准空腔与文献[28]验证算例中选取的腔体相同，均为M219腔体，属于典型开式空腔，尺寸：长为0.508 m，宽和深均为0.101 6 m，长深比为5∶1. 欧洲QinetiQ组织对M219空腔进行了多轮风洞实验得到了可信的实验数据[29]，模型几何尺寸如图1(a)所示，实验中在腔体底板等间距的布置了10个压力监测点，如图1(b)所示。在M219腔体模型的基础上进行修改，施加本文选取的控制措施，如图1(c)所示。将腔体尾部后壁板替换为开孔板，同时在开孔板后部连接封闭矩形腔，将其称作耗能腔。开孔半径为2 mm，布置为梅花形，关于开孔大小及开孔方式的影响将在后续研究中进一步分析，本文不做详细论述。与风洞实验相同，在底板布置10个压力监测点，此外，沿着腔体上底板中心线均匀的设置400个压力监测点，以得到腔体上底板压力随时间变化历程。

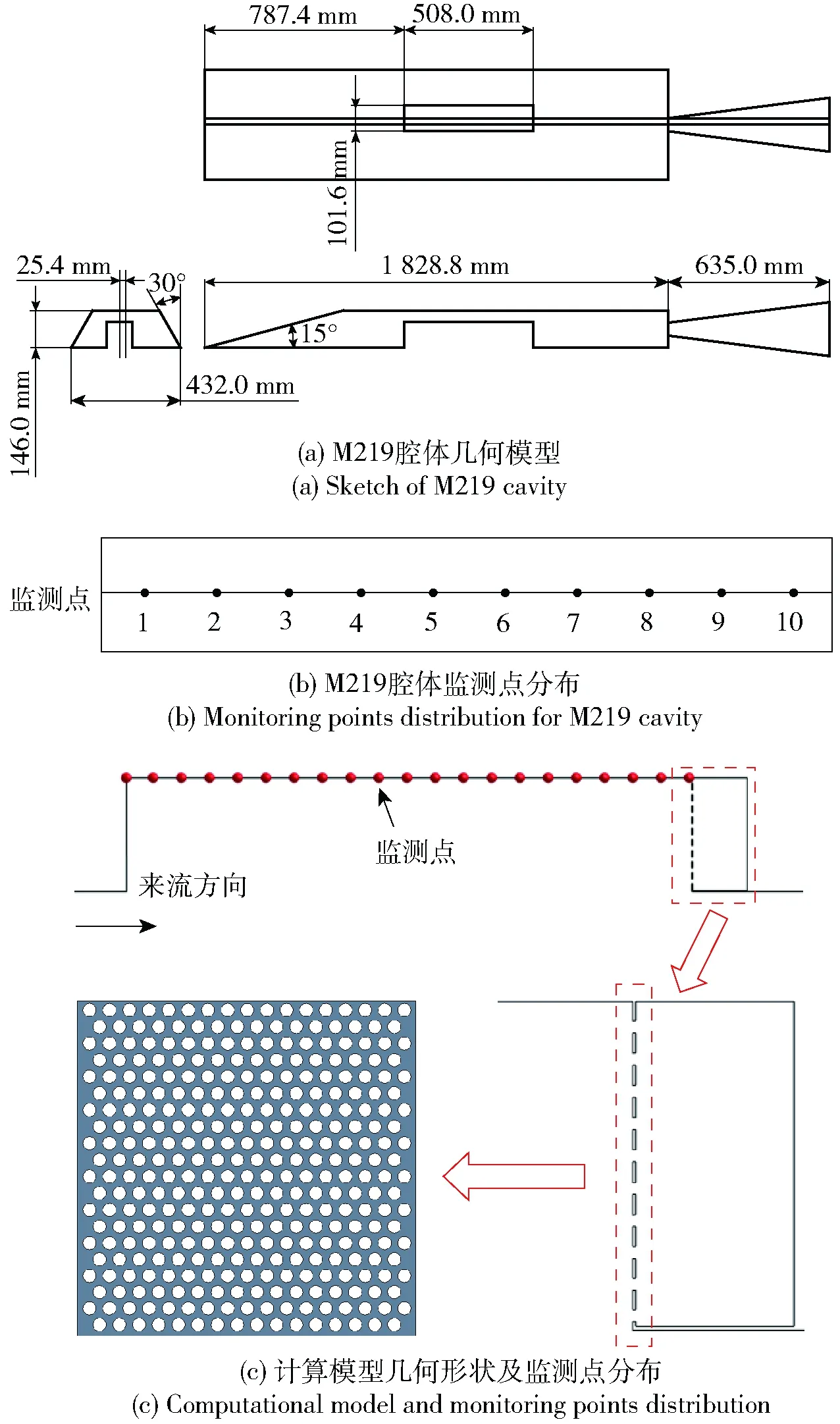
图1 基准M219腔体及计算模型几何形状Fig.1 Base M219 cavity and computational model

2.2 网格划分

在划分网格时选用非结构化Trim网格，壁面附近生成附面层网格，垂直壁面方向第1层网格尺寸设置为2×10-6m，可以保证y+近似为1. 腔体内网格尺度为1 mm，后壁板开孔位置网格进行了加密，网格尺度为0.2 mm，总网格数目约为1 580万。腔体中心截面网格分布如图2所示。

图2 腔体中心截面网格分布Fig.2 Grid distribution on central plane of cavity

2.3 计算条件及工况

分别对亚声速及超声速来流条件下，选取的控制措施对腔体内气动噪声抑制效果进行了研究。亚声速条件下来流马赫数Ma=0.85，静压p=63 kPa，静温T=266.5 K；超声速条件下来流马赫数Ma=1.35，静压p=36 kPa，静温T=223.5 K. 来流迎角为α=0°，计算远场条件设置为远场自由来流条件，腔体壁面均采用无滑移壁面条件。选取了3种不同的耗能腔尺寸，孔径r为2 mm，耗能腔长度l分别为50 mm、100 mm和200 mm，针对不同马赫数及采取的控制措施，共计算了4种工况，详见表1. 计算时间步长选取为1×10-5s，非定常计算采用双重时间步法，内迭代步设置为20步，可以保证残差下降两个量级。

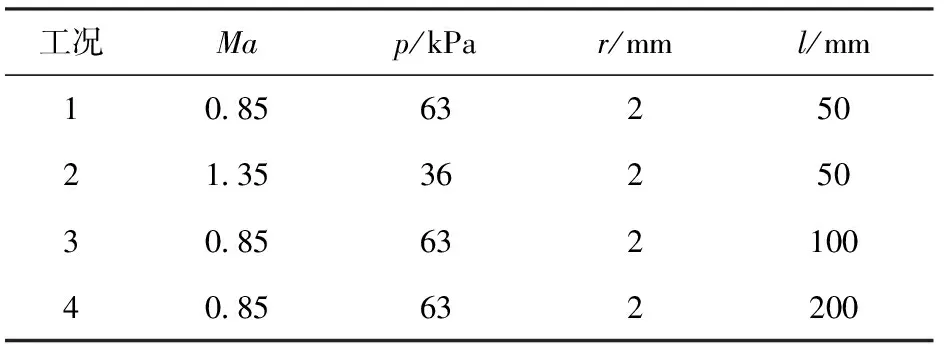
表1 计算工况

3 结果分析

3.1 声压级频谱分析

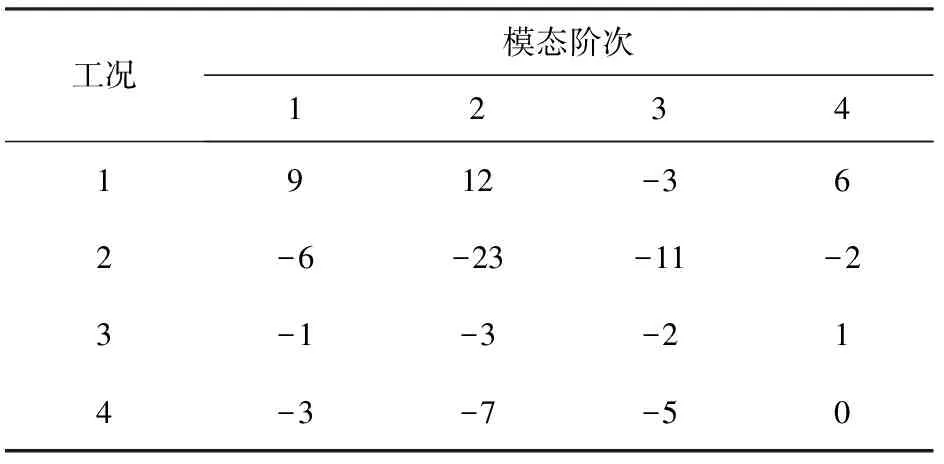
表2给出了基准M219腔体亚、超声速来流条件下噪声最高点监测点10的各阶模态声压级实验值，表3及图3(a)给出了本文4种工况中计算得到监测点10的各阶模态声压级结果。表4及图3(b)为与基准M219空腔相比各阶模态噪声幅值变化量，图中负值表示采取控制措施后噪声得到抑制，正值表示噪声升高。

表2 基准M219腔体声压级幅值

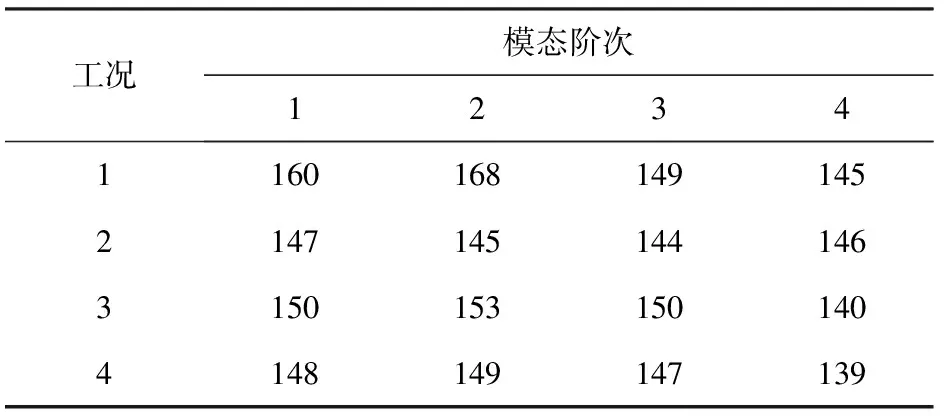
表3 各工况声压级幅值

从表4可以看出工况2、工况3和工况4中腔体内气动噪声水平得到了有效的抑制，然而工况1中噪声反而高于基准腔体，与基准情况相比噪声升高最大幅值达到12 dB. 工况2噪声降低幅度最大，腔体内各阶模态噪声均得到了较好的抑制，噪声降低最大幅值为23 dB.

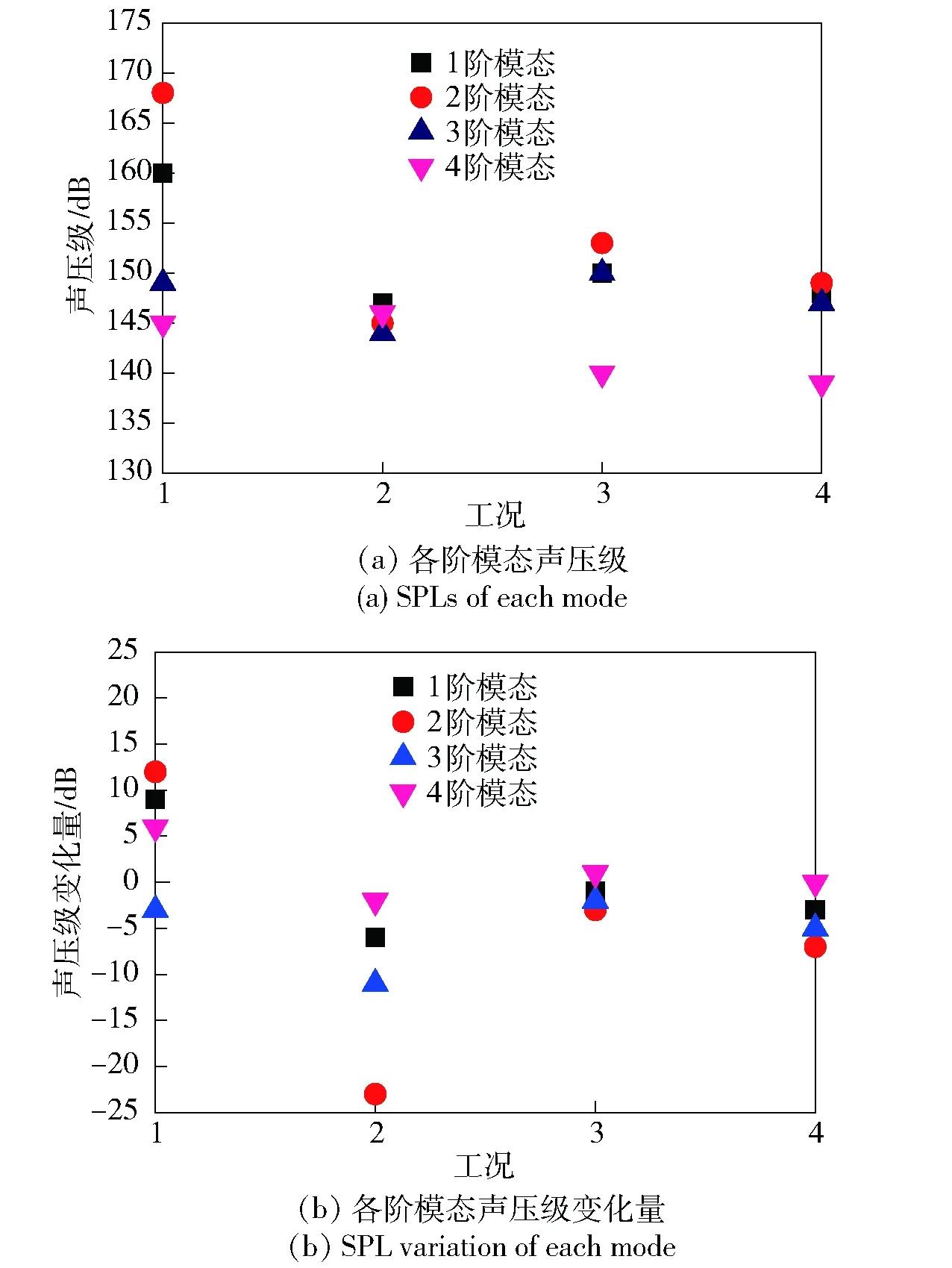
图3 不同工况下腔内1～4阶模态声压级幅值Fig.3 SPLs of modes 1 to 4 for different cases

dB

图4和图5分别给出了采取相同控制措施之后，工况1亚声速(Ma=0.85)及工况2(Ma=1.35)超声速来流条件下，腔体内监测点6(x/L=0.55，x表示到腔体前缘的距离)和监测点10(x/L=0.95)的声压级频谱图。从图4可看出，工况1腔内噪声水平不但没有得到有效抑制反而大幅度升高，与未采用控制措施的基准M219空腔相比，腔体内2阶模态噪声升高幅度最大，约为12 dB. 在基准M219腔体内2阶、3阶模态幅值相差较小，存在两个主导模态，采取控制措施之后腔体内2阶模态噪声幅值远高于1阶、3阶模态，变为腔体内唯一的主导模态，其频率值也由356 Hz降低为254 Hz.

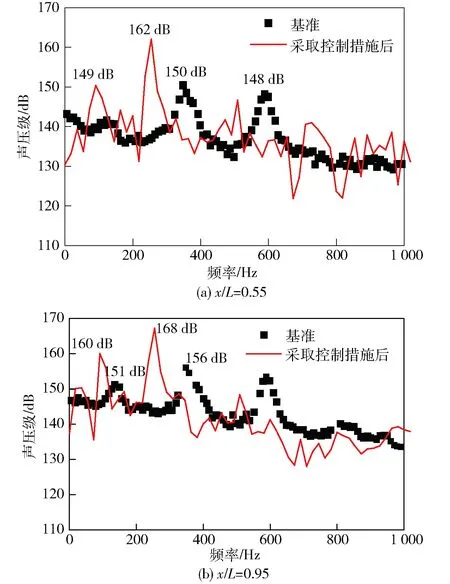
图4 工况1腔内声压级频谱特性Fig.4 SPL along the center line of cavity bottom in Case 1

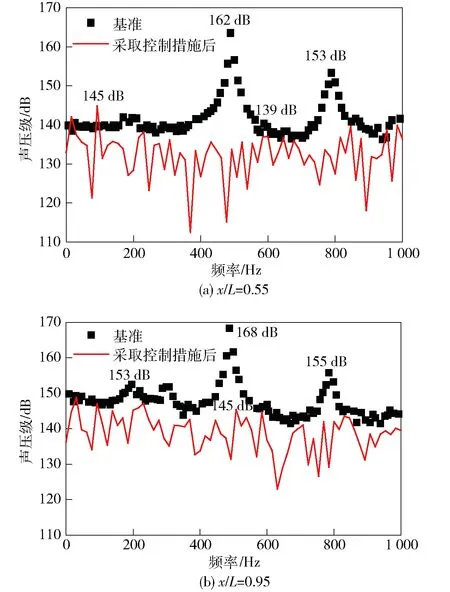
图5 工况2腔内声压级频谱特性Fig.5 SPL along the center line of cavity bottom in Case 2

从图5可以看出，超声速条件下采取与工况1相同的控制措施之后，腔体内部噪声水平被有效抑制，各阶模态纯音噪声消失，均降低到与宽频噪声相同的量级，腔体内噪声最高降幅为23 dB.

由上述分析可知，亚声速来流条件下，耗能腔尺寸过小时会使开式空腔内噪声环境恶化，然而超声速条件下小尺寸耗能腔可以对气动噪声起到良好的抑制效果。亚声速条件下，随着耗能腔尺寸增大，控制措施对噪声的抑制效果逐步提升。

3.2 流场结果分析

3.2.1 工况1亚声速流场结果分析

通过腔体上底板设置的400个压力监测点得到压力随时间变化历程，如图6所示。图6中横坐标表示距腔体前缘的相对位置(腔体前缘位置取为x/L=0，腔体尾缘为x/L=1)，纵坐标表示时间，颜色条表示压力值大小。从图6中可以清晰地观察到在腔体后部存在着周期性的高压区，这是由于脱落涡撞击腔体尾缘产生的。在腔体前部同样可以观察到周期性的高压区，但其压力幅值明显低于后部的高压区。前部高压区出现的频率与后部高压区出现的频率相同，但存在相位差。

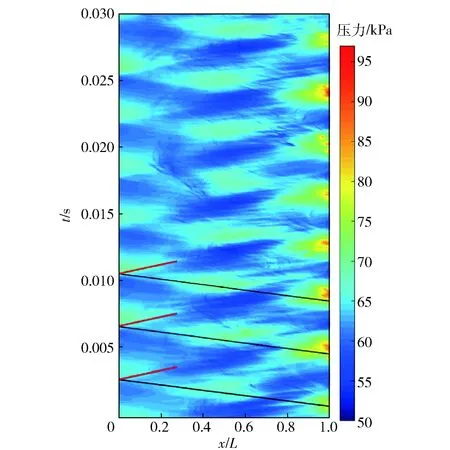
图6 工况1腔体上底板压力与时间分布云图Fig.6 Pressure versus time at cavity upper floor in Case 1

从图6中不仅可以得到腔体上底板不同时刻、不同位置处的压力分布，还可以反映出腔体内压力波随时间的传播过程。图6中黑色线标示的为一组斜率近似为常数的压力波，其斜率为负，表明压力波随着时间的推移由腔体后缘向腔体的前缘运动，即为一组向前传播的压力波。可以看出黑色标线恰好连接了腔体前缘和尾缘的两个高压区，前缘高压区的出现时间滞后于尾缘高压区。图6中黑色标线的斜率即为该压力波的传播速度，通过测量得到斜率值约为300 m/s，接近于腔体内声速。结合上述分析，黑色标线所示的一系列压力波为腔体内部的前传声波，前传声波由脱落涡与腔体尾缘撞击产生，在腔体内部向前传播，当到达腔体前缘时与前壁板发生碰撞，使前缘压力升高，同时对前缘剪切层产生干扰，使其失稳产生新的脱落涡。

表5为工况1不同时刻腔体中心截面流场马赫数、压力及数值纹影云图，表中共给出了0～0.006 5 s的结果，对应于图6中0～0.006 5 s，表5中t=0 s对应于图6中t=0 s时刻。从表5中t=0 s的压力分布云图可看出，此时前传声波刚好传播到腔体前缘并与前壁板碰撞，造成前缘压力升高，从马赫数云图及数值纹影图中可以看出，前传声波诱发了剪切层的失稳。

纯空腔内剪切层会发生上下摆动[6]，从表5中数值纹影图中可观察到工况1采取控制措施之后剪切层同样存在明显的上下摆动。由表5中t=0 s的数值纹影云图可知，此时剪切层偏离腔体上底板下摆，这是由于前缘压力较高，剪切层被向外挤压的结果。此时剪切层失稳产生的脱落涡存在一个向下偏斜远离腔体上底板的速度分量，将之称为下摆脱落涡，标记为X1(X表示涡结构下偏，1为序号，后文X2表示第2个下摆脱落涡)。另外可以观察到腔体中部还存在靠近上底板的脱落涡，将其称为上摆脱落涡，标记为S1(S表示涡结构上偏)。随着时间的推移，X1和S1同时向腔体后部传播。由于S1靠近腔体内部，因此其传播的速度要小于更加靠近主流的X1.

从图6还可看出，前传声波与腔体前缘碰撞后产生反射声波(图中红色标线所示)，在向腔体后部传播过程中其强度逐渐降低，最终在x/L=0.3位置消失。紧接着在腔体底板又出现一个向后传播的低压带(图中蓝色区域)。从表5中t=0.002 0 s和t=0.006 0 s的压力云图中可清楚地看到，下摆脱落涡附近区域形成了明显的低压区，其范围影响到了腔体上底板，因此腔体底板向后传播的低压带即受到下摆脱落涡的影响产生的。

由表5中t=0.002 0 s的数值纹影云图可知，S1传播到腔体尾部并与尾缘撞击发声，从压力云图可以看出，撞击使得腔体尾部形成高压区。由于采取的控制措施将腔体后壁板由实体板替换为开孔板，因此撞击气流沿着开孔流入后面的耗能腔，起到了缓冲撞击强度的作用。由于S1偏向上底板，脱落涡携带的气流流量仅有小部分越过尾缘向后传递，绝大部分气流留在腔体内部，使得整个后壁板上的开孔均向耗能腔内注入气流。图7(a)为后壁多孔板开孔处及耗能腔内的速度矢量图，从图中可以看出气流流动方向均指向耗能腔内部。然而由于耗能腔容积有限，过多气流的注入导致耗能腔内气流无法进行循环，只能不断积蓄使其内部压力不断升高，甚至超过了开式空腔后部区域的压力值，如表5中t=0.002 0 s和t=0.002 5 s的压力云图所示。

表5 工况1在不同时刻的腔体中心截面马赫数、压力和数值纹影云图

Tab.5 Mach number, pressure and numerical schlieren contours on central plane of cavity in Case 1 at different times

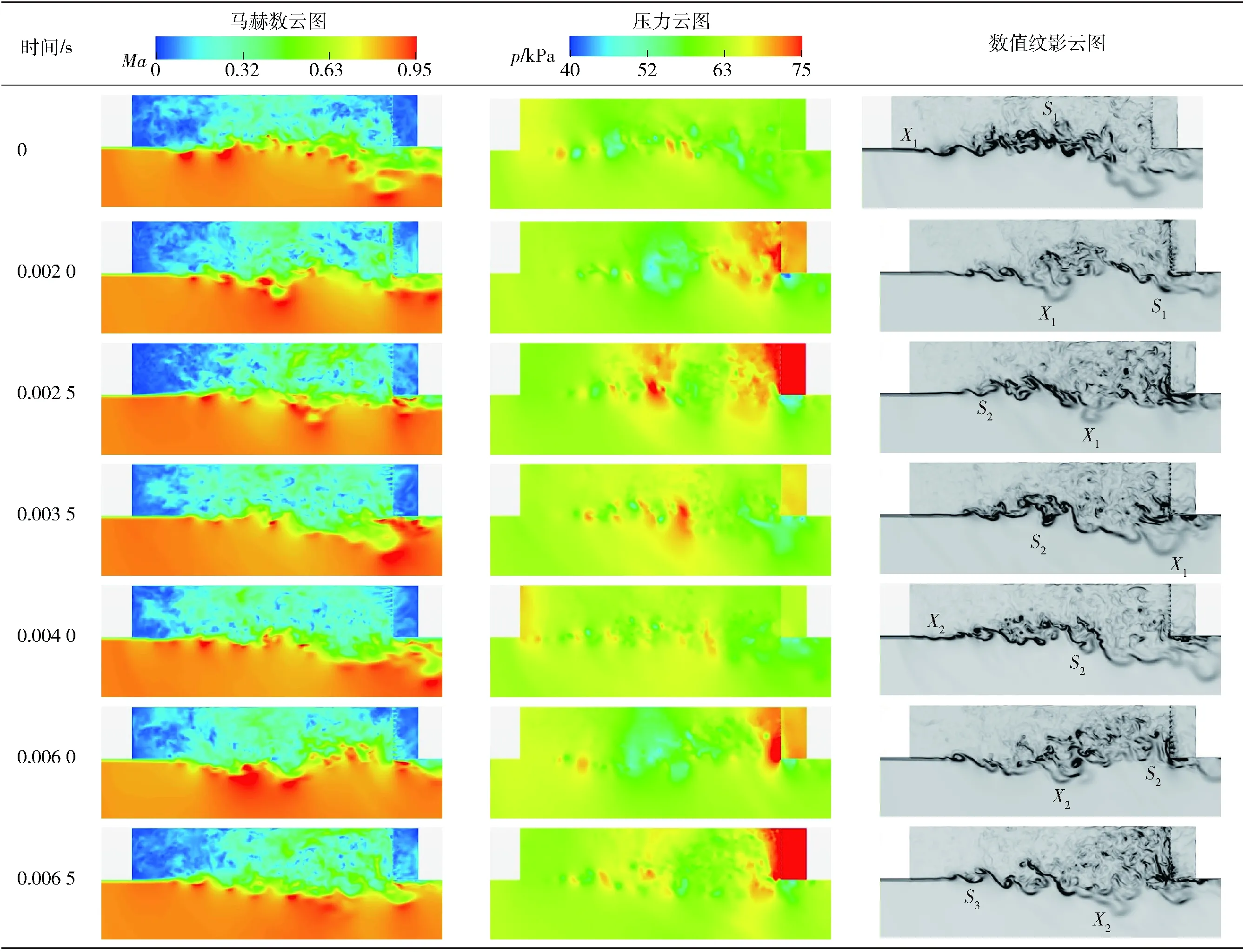
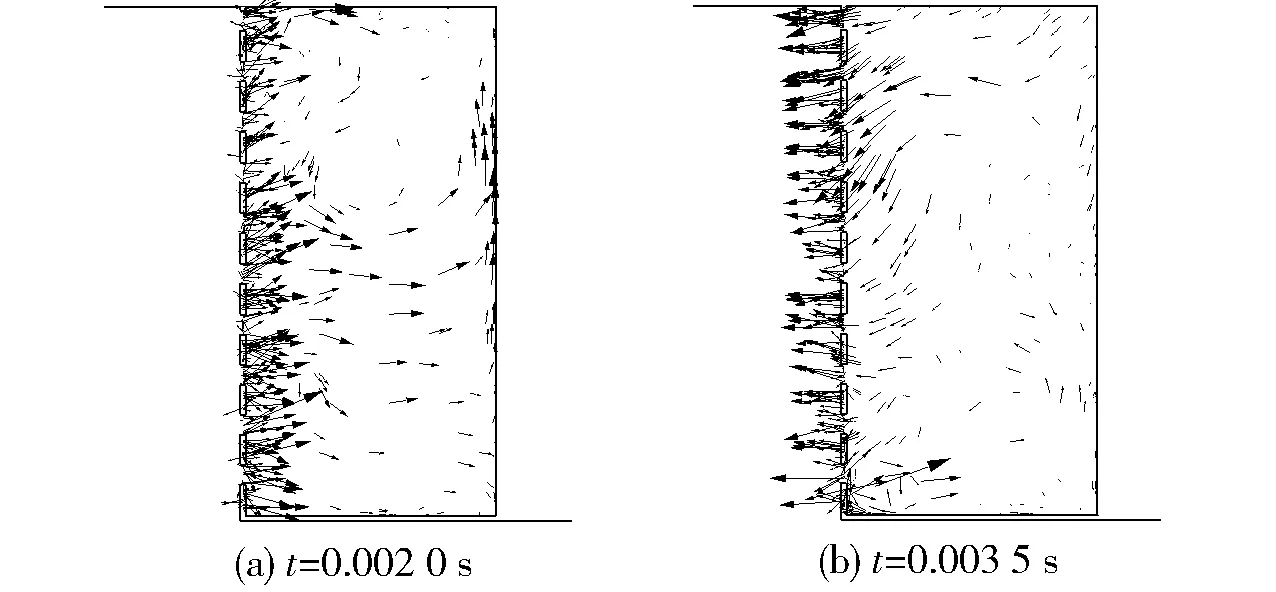
图7 工况1后壁板圆孔及耗能腔速度矢量图Fig.7 Velocity vectors at rear wall holes and in dissipative cavity in Case 1

从表5中t=0.002 5 s的数值纹影云图还可以观察到，前缘剪切层失稳又形成新的脱落涡，由于此时前缘压力较低，所以剪切层偏向腔体上底板上摆，该脱落涡是一个上摆脱落涡，将其标记为S2. 与X1相比，S2存在明显的不同：X1是由前传声波诱发剪切层失稳产生，其形成位置靠近前缘(约为x/L=0.08)，且前传声波与腔体前壁板碰撞使得前缘压力升高，迫使剪切层向下摆动；然而S2形成位置明显更加靠后(约为x/L=0.15)且S2形成时前缘压力较低，剪切层上摆，因此S2并非前传声波所诱发，表明Xi与Si为不同的两类脱落涡。

在t为0.002 5～0.003 5 s时间段，X1运动到腔体尾缘，由于其逐渐远离腔体上底板向下偏移，因此并未与尾缘发生撞击，而是直接越过尾缘向后传播。这导致腔体后部区域压力下降，而此时后部耗能腔内压力很高。从表5中t=0.003 5 s的马赫数分布云图中可以清晰地看到，后部耗能腔通过后壁多孔板在短时间内向开式空腔注入大量气流。图7(b)给出了多孔板开孔处及耗能腔内的速度矢量图，从图中可以看出气流流动方向均由耗能腔指向开式空腔，这部分注入的气流在开式腔体内部形成高强度回流，增强了对腔体前缘剪切层的扰动。

从表5中t=0.004 0 s的压力分布和数值纹影云图可以看出，由S1撞击产生的前传声波传递到腔体前缘，引起前缘压力再次升高。前传声波扰动剪切层再次失稳，诱发产生新的下摆脱落涡，将其标记为X2. 从表5中t=0.006 0 s的压力分布和数值纹影云图可以看出，S2与尾缘撞击发声，耗能腔内再次大量注入气流，内部压力升高。S1与S2撞击发声的时间间隔约为0.004 s，与图6中腔体后部周期性出现的高压区的时间间隔相同，从图4得到的声压级2阶主导模态的频率值为254 Hz，二者恰好吻合，表明腔体内2阶主导模态噪声为上摆脱落涡与尾缘撞击产生。

从表5中t=0.006 5 s的压力分布和数值纹影图可以看出，腔体前缘位置处形成了第3个上摆脱落涡，将其标记为S3. 由3.2.1节分析可知，其并非前传声波所诱发，同时形成位置距离腔体前缘较远，因此应当是由于腔体后部产生的扰动向前传播所导致。在t=0.003 0 s时，后部耗能腔向开式空腔内注入了大量的气流流量，形成较强的回流。通过对流场进行分析，得到回流的平均速度约为120 m/s，回流产生到腔体前缘剪切层上摆失稳的时间间隔约为0.003 5 s，二者基本相互吻合。因此认为上摆脱落涡的形成是由于耗能腔内积蓄的气流迅速注入开式空腔，从而形成较强回流对剪切层产生干扰，使其发生失稳而产生的。

从上述分析可知，工况1腔体内存在两种类型的脱落涡：上摆脱落涡和下摆脱落涡。上摆脱落涡与腔体尾缘撞击并辐射声波，声波在腔体内部向前传播，扰动前缘剪切层失稳形成下摆脱落涡。撞击还使得后部压力升高，撞击气流通过后壁板开孔流入耗能腔，由于撞击强度大且耗能腔尺寸较小，导致耗能腔内气流无法循环，只能不断积蓄使得耗能腔内压力持续升高。此后下摆脱落涡传播到腔体尾缘，由于其向下偏移，并不与尾缘发生撞击而是直接越过尾缘向后传播，因此腔体后部压力下降。此时处于高压状态的耗能腔向开式空腔内大量注入气流，形成较强的回流。回流运动到腔体前部时对剪切层产生扰动，诱发了新的上摆脱落涡形成，从而腔体内出现不同于基准M219腔体的新自持振荡循环。

亚声速条件下选取的控制措施主要问题在于：由于耗能腔尺寸过小，撞击气流大量注入后，在耗能腔内无法进行循环，没有起到消耗气流能量的作用。而且大量气流的积蓄导致腔体内压力不断升高，之后积蓄的气流又快速注入到开式空腔，形成较强的回流，引起前缘剪切层失稳，诱发新的脱落涡生成。其不但没有减弱自持振荡循环，反而起到了加强自持振荡强度的反作用，因此腔体内气动噪声不降反升。

3.2.2 工况2超声速流场结果分析

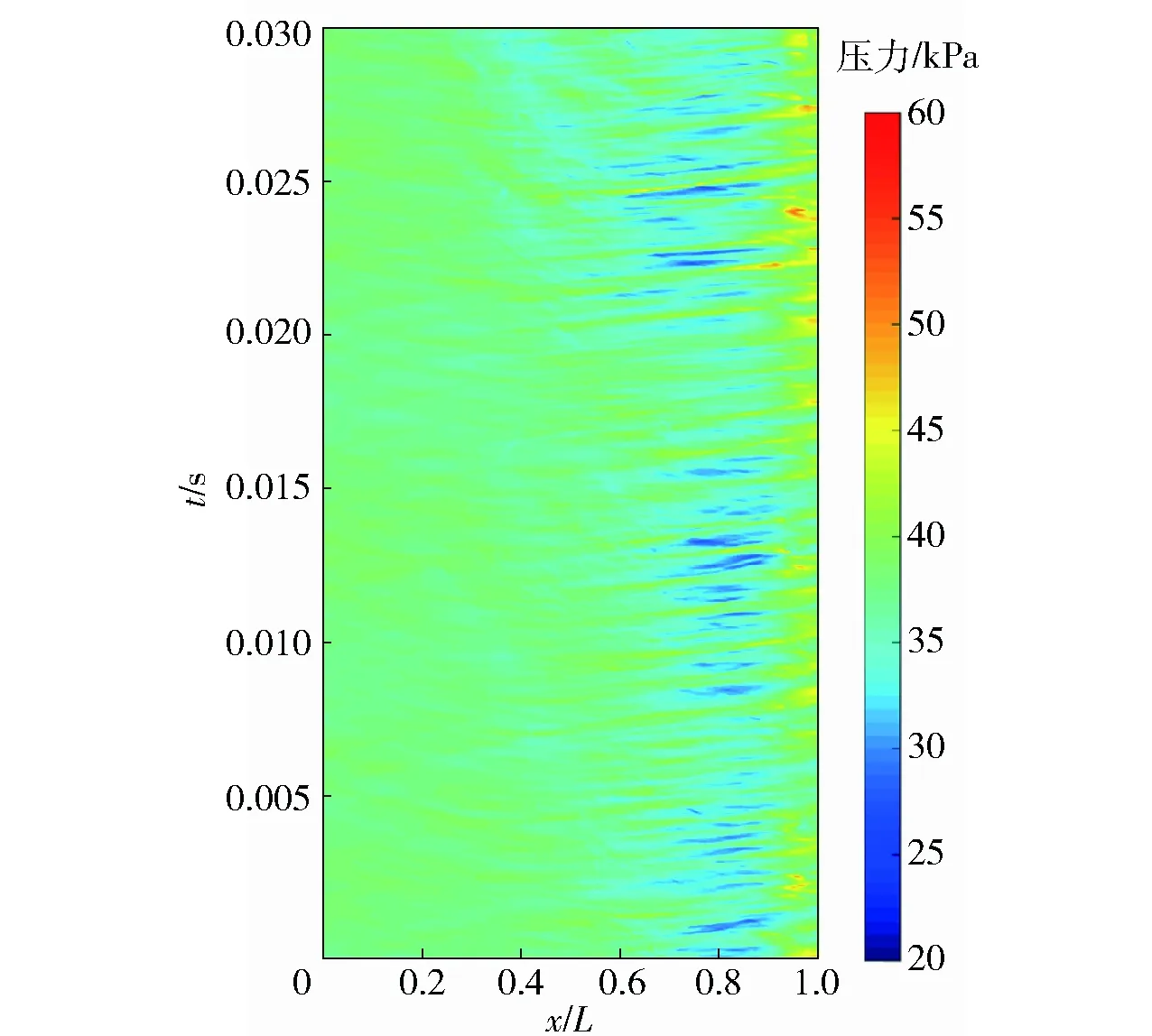
图8 工况2腔体上底板压力与时间分布云图Fig.8 Pressure versus time at cavity bottom in Case 2

图8为超声速来流条件下，腔体上底板设置的400个压力监测点得到的压力随时间变化历程，与图6亚声速来流条件下得到的结果相比较，二者存在显著的差异。亚声速条件下存在于腔体尾缘处的高强度、周期性的高压区变成了超声速条件下高频率、低强度的高压脉动。这表明腔体内没有形成周期性的高强度脱落涡与腔体尾缘发生撞击，而是存在一系列低强度涡结构与尾缘碰撞。腔体内不存在明显的自持振荡循环，没有产生主导模态的纯音噪声，这与图5声压级频谱图中得到的结果相一致。说明超声速来流条件下，在腔体尾缘采取控制措施之后，腔体内的自持振荡环节被中断，腔体内噪声水平得到了有效地控制。

表6为超声速条件下、不同时刻腔体中心截面流场马赫数、压力及数值纹影云图，表中共给出了0～0.002 0 s的流场结果，即图8中的0～0.002 0 s，表6中t=0 s对应于图8中t=0 s时刻。随着来流马赫数由亚声速增加到超声速，腔体唇口剪切层中对流马赫数增大，剪切层稳定性增强[30]，因此工况2中剪切层的稳定性较工况1更强。从马赫数分布云图及数值纹影图中可以看出，剪切层失稳点更加远离前缘(约为x/L=0.3)，且剪切层并未出现大幅度的上下摆动，剪切层内形成的脱落涡近似水平地向尾缘传播。从压力分布云图中可以看出尾缘撞击点位置处压力升高，但耗能腔内压力没有大幅度上升。

表6 工况2在不同时刻的腔体中心截面马赫数、压力和数值纹影云图

Tab.6 Mach number, pressure and numerical schlieren contours on central plane of cavity in Case 2 at different times

图9(a)给出了此时后壁板开孔及耗能腔内速度矢量图。从图9(a)中看出，当剪切层内涡结构与尾缘发生撞击时，一部分气流通过后壁板上的开孔流入耗能腔中，多孔板起到了泄流、降压的作用，减弱了涡结构与尾缘撞击的强度，使得撞击产生的噪声幅值降低，减弱了前传声波的强度并削弱前传声波对前缘剪切层的扰动。由于脱落涡近似水平地传递到尾缘，并未向腔体上底板偏转，因此一部分撞击气流直接越过腔体向后传播，留存在腔体内的撞击气流流量减小。流量减小使得仅下半部分开孔向耗能腔中注入气流，与此同时耗能腔内气流经由后壁板上部开孔流回开式空腔。流入的高速气流在耗能腔内循环流动并形成涡旋，在这个过程中气流所携带的能量逐步被消耗。图9(b)给出了后壁板孔洞的总压恢复系数分布云图，从图中可以看出开孔板上部开孔处气流总压明显小于下部，证明下部流入的高速气流的能量被显著地的消耗。由图9(a)也可以看出由开孔板上部流入开式空腔的气流与下部流入耗能腔的气流相比其流速显著降低，回流速度降低使得开式空腔内回流强度减弱。

图9 工况2后壁板开孔及耗能腔速度矢量图与总压恢复系数云图Fig.9 Velocity vector and total pressure recovery coefficient contour of airflow at rear wall holes and in dissipative cavity in Case 2

前传声波强度及腔内回流强度降低使腔体前缘剪切层受到的扰动减小，剪切层可以稳定向后传播到更远的距离，失稳点位置更加靠后，剪切层摆动幅度及脱落涡强度降低，进一步减弱剪切层内涡结构与尾缘撞击强度，从而形成良性循环。从表6中可以发现：在t=0.002 0 s内腔体后壁板下半部分开孔持续向耗能腔内注入气流，在耗能腔内循环过程中不断消耗气流的能量，并使其以较低的速度由上部开孔流回空腔，耗能腔内一直未出现大幅度的压力攀升；空腔前缘压力随时间无明显变化，前缘剪切层未出现明显的上下摆动，剪切层失稳点位置基本保持不变，腔体内未出现周期性的高强度脱落涡与尾缘发生撞击，腔体内未产生高强度压力脉动，自持振荡循环被终止。

可见所采取的控制措施起到了两个方面的作用：一是通过多孔板泄流、降压，减弱了脱落涡与尾缘的撞击强度，减小了撞击产生的噪声幅值，降低了腔体内噪声水平，并削弱了前传声波对前缘剪切层的扰动；另一方面，耗能腔不断消耗开孔板下部流入的气流能量，使其以较低的速度流回开式空腔，降低了回流的强度，减弱了对前缘剪切层的扰动。在上述因素共同作用下，引言中提到的自持振荡循环中第2、第3个环节得到了有效地控制，腔体内自持振荡循环被终止，无高幅值的纯音噪声产生，腔体噪声水平得到了有效地控制。

3.3 耗能腔长度的影响

工况1、工况3和工况4中耗能腔的长度l分别选取为50 mm、100 mm和200 mm，来流均为亚声速Ma=0.85. 由图3可知，随着后部耗能腔长度的增加，采取的控制措施对腔体内噪声水平的抑制效果也逐渐增强。耗能腔长度选为50 mm时，与基准工况相比，腔体内气动噪声不但没有减小，反而大幅度升高；当耗能腔长度增加到100 mm时，工况3中腔体内部噪声幅值较基准工况有所下降，腔体内各阶模态声压级均有所降低；当继续增加耗能空腔的长度到200 mm时，腔体内噪声水平得到了良好地抑制，各阶模态噪声水平均大幅降低，声压级最大降幅为7 dB. 可以看出耗能腔尺寸应满足l/L≥0.2，才能保证亚声速条件下，腔体内噪声水平得到抑制。

在3.2.1节中，详细分析了工况1噪声水平升高的原因，由于撞击强度较大，后壁板所有开孔均向耗能腔内注入气流，加之耗能腔尺寸较小、容积有限，导致耗能腔内气流积蓄，压力持续升高，无法进行循环，并未起到耗能的作用。此后又在短时间内向开式空腔注入了大量积蓄的气流，使腔体内形成很强的回流，增强了气动噪声。

表7给出了工况3及工况4流场马赫数、压力及数值纹影云图，图中所选时刻刚好为脱落涡与腔体尾缘发生撞击。图10给出了此时后壁板开孔及耗能腔内速度矢量图。从表7压力分布云图中可以看出，脱落涡的撞击使得腔体尾缘出现局部高压，但其范围较小。从图10可以看出，撞击气流经由后壁开孔板下部孔洞流入耗能腔，起到了缓冲撞击强度、泄除撞击气流流量、降低尾缘撞击压力峰值的作用。从表7中可以看出，注入的气流引起后部耗能腔压力有所升高，但其升高幅度有限，并未出现如工况1一样的压力大幅攀升现象。这是由于耗能腔长度增加后，其体积增大，对撞击气流的容纳能力增强。从图10中还可以看出：两种工况后壁板上部开孔均由耗能腔向开式空腔注入气流，气流在耗能腔内能不断进行循环流动并持续消耗能量；流出耗能腔的气流速度小于流入的气流速度，回流流速的下降减弱了回流强度，降低了回流对腔体前缘的扰动。图11为两种工况后壁板开孔的总压恢复系数分布云图，可以看出开孔板上部开孔内气流的总压明显小于下部开孔气流的总压，下部流入的高速气流能量被显著地消耗。从表7中马赫数分布云图及数值纹影图可以看出，与工况1相比，两种工况流场中剪切层及其内部的涡结构未出现明显的上下摆动，基本保持水平，剪切层失稳点位置约为x/L=0.18.

表7 工况3、工况4腔体中心截面马赫数、压力和数值纹影云图

Tab.7 Mach number, pressure and numerical schlieren contours on central plane of cavity in Cases 3 and 4

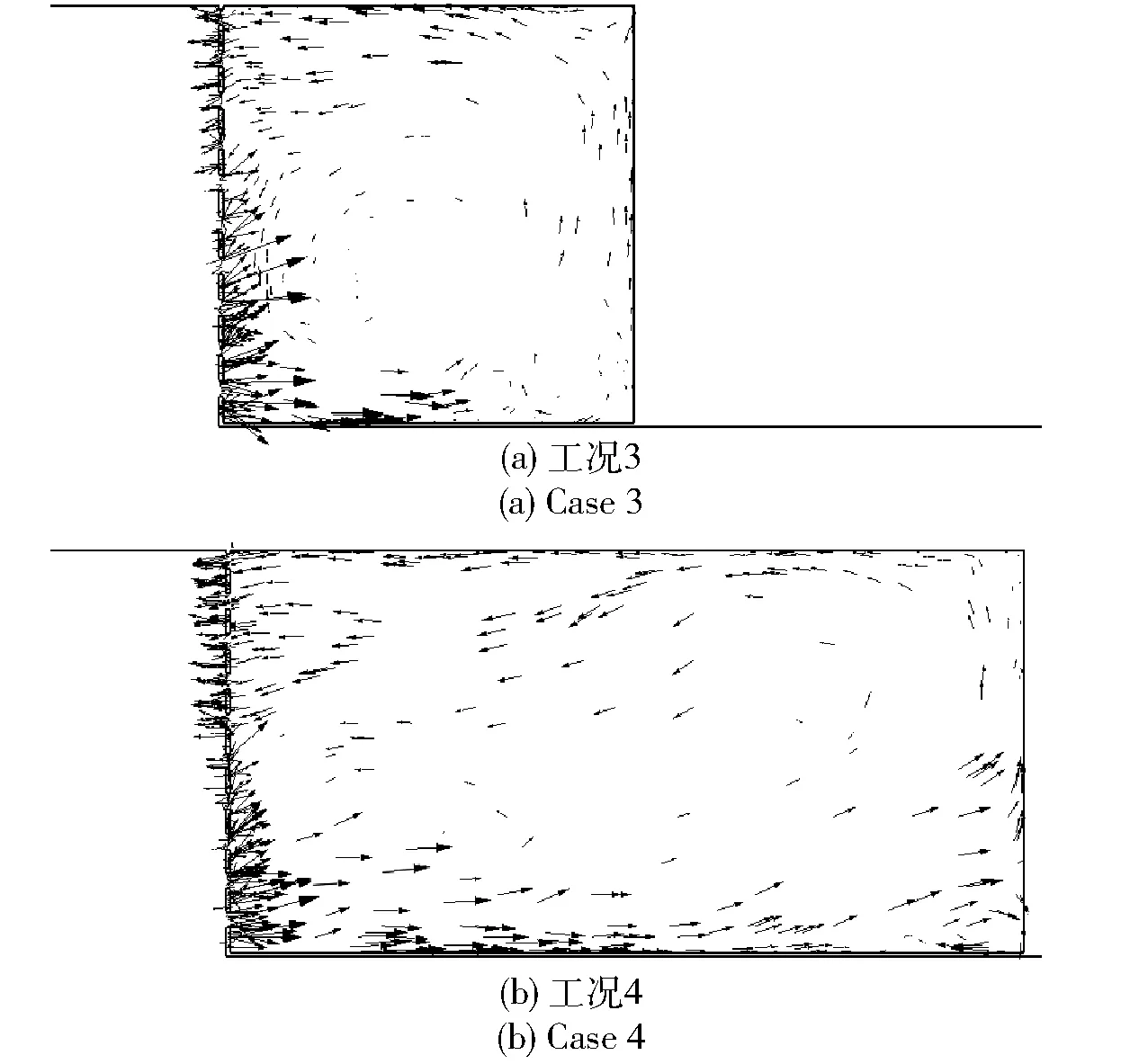
图10 工况3和工况4后壁板圆孔及耗能腔速度矢量图Fig.10 Velocity vector of airflow at rear wall holes and in dissipative cavity in Cases 3 and 4

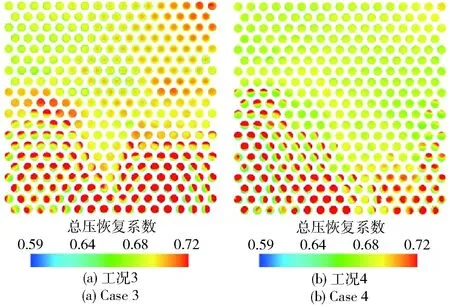
图11 工况3和工况4后壁板圆孔总压恢复系数分布云图Fig.11 Total pressure recovery coefficient contours of airflow at holes on rear wall in Cases 3 and 4

综合上述分析可知，增加耗能腔的长度可以使其更加有效地缓冲脱落涡与腔体尾缘的撞击，减缓撞击发声强度，降低腔体内噪声水平及前传声波的强度。容积的增加使耗能腔可以更好地泄除撞击气流流量，避免了工况1中出现的耗能腔内积蓄的气流快速注入开式空腔形成高强度回流，诱发前缘剪切层失稳的问题。耗能腔长度的增加还使得流入的高速气流可以在腔内循环流动，并在这个过程中不断消耗能量，最终以较低的速度从后壁板上部开孔流回开式空腔，降低了腔体内回流的强度，减弱了对前缘剪切层的扰动，剪切层失稳点后移，上下摆动幅度降低。因此可以看出当耗能腔长度增加之后，所选取的控制措施可以同工况2超声速条件下一样，使腔体内自持振荡循环被削弱或终止，从而使开式空腔内部噪声水平得到有效地抑制。

4 结论

1)通过数值纹影方法等流场分析技术研究了腔体内自持振荡循环的各个过程，得到了腔体底板压力随时间变化历程，明确了控制措施对流场及气动噪声产生影响的内在机理。后壁多孔板起到了泄流、降压、缓冲脱落涡撞击强度的作用，降低了撞击发声幅值。耗能腔容纳了撞击气流并消耗其能量，使其以较低速度流回开式腔体，减弱了回流强度，降低了对前缘剪切层的扰动。使得腔体内自持振荡循环被减弱或终止，从而噪声水平得到抑制。

2)超声速来流条件下，本文选取的多孔板加耗能腔的控制措施能够终止开式空腔内的自持振荡循环，使腔体内各阶模态频率纯音噪声消失，有效地抑制腔体内气动噪声水平，腔体内噪声最大降幅达23 dB.

3)亚声速来流条件下，控制措施的效果与耗能腔尺寸的选取密切相关。当耗能腔尺寸过小时，腔体内噪声水平不但没有被抑制反而大幅增强，最高升幅达12 dB. 增加耗能腔尺寸后，开式空腔内噪声水平得到抑制，且噪声降低幅度随着耗能腔尺寸的增加而增大。

)

[1] Krishnamurty K. Acoustic radiation from two dimensional rectangular cutouts in aerodynamic surfaces, TN 3487 [R]. Pasadena, CA, US: California Institute of Technology, 1955.

[2] Charwat A F. An investigation of separated flows-part I: the pressure field[J]. Journal of the Aerospace Sciences, 1961, 28(5): 457-470.

[3] Rossiter J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R]. Farnborough: Royal Aircraft Establishment, 1964.

[4] Heller H H, Holmes D G, Covert E E. Flow induced pressure oscillations in shallow cavities[J]. Journal of Sound and Vibration, 1971, 18(4):545-546.

[5] Covert E, Bilanin A J. Estimation of possible excitation frequencies for shallow rectangular cavities[J]. AIAA Journal, 1973, 11(3):347-351.

[6] 黎军, 李天, 张群峰. 开式流动腔体的流动机理与控制[J]. 实验流体力学, 2008, 22(1): 80-83.

LI Jun, LI Tian, ZHANG Qun-feng. The mechanism and control of open cavity flow[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1):80-83. (in Chinese)

[7] 黎军, 张群峰, 曾宏刚, 等. 腔体闭式流动控制的实验和数值模拟[J]. 北京航空航天大学学报, 2008, 34(1): 96-99.

LI Jun, ZHANG Qun-feng, ZENG Hong-gang. Experiment and numerical investigation of controls for closed cavity flow[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(1): 96-99. (in Chinese)

[8] Givogue G, Vakili A, Fowler W.An experimental investigation of 2-D cylinders affecting supersonic cavity flow[C]∥29th AIAA Applied Aerodynamics Conference. Honolulu, HI, US: AIAA, 2011.

[9] Thieman C C, Vakili A. An experimental investigation of supersonic cavity flow control with vertical cylinders[C]∥43rd AIAA Fluid Dynamics Conference. San Diego, CA, US: AIAA, 2013.

[10] 刘瑜, 童明波. 基于DDES算法的有扰流片腔体气动噪声分析[J]. 空气动力学学报, 2015, 33(5): 643-648.

LIU Yu, TONG Ming-bo. DDES of aero-acoustic over an open cavity with and without a spoiler[J]. Acta Aerodynamica Sinica, 2015, 33(5): 643-648. (in Chinese)

[11] 余培汛, 白俊强, 郭博智. 剪切层形态对开式空腔气动噪声的抑制[J]. 振动与冲击, 2015, 34(1): 156-164.

YU Pei-xun, BAI Jun-qiang, GUO Bo-zhi. Suppression of aerodynamic noise by altering the form of shear layer in open cavity[J]. Journal of Vibration and Shock, 2015, 34(1): 156-164. (in Chinese)

[12] 吴继飞, 徐来武, 范召林, 等. 开式空腔气动声学特性及其流动控制方法[J]. 航空学报, 2015, 36(7): 2155-2165.

WU Ji-fei, XU Lai-wu, FAN Zhao-lin, et al. Aero acoustic characteristics and flow control method of open cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2155-2165. (in Chinese)

[13] 陶洋, 吴继飞, 徐来武, 等. 基于前缘边界层扰动的空腔压力脉动抑制研究[J]. 实验流体力学, 2016, 30(3):66-70.

TAO Yang, WU Ji-fei, XU Lai-wu, et al. Control of cavity flow pressure oscillation through leading edge boundary layer perturbation[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3):66-70. (in Chinese)

[14] Williams D, Cornelius D, Rowley C.Closed-loop control of linear supersonic cavity tones[C]∥45th AIAA Fluid Dynamics Conference. Miami, FL, US: AIAA, 2007.

[15] 杨党国, 吴继飞, 罗新福. 零质量射流对开式空腔气动噪声抑制效果分析[J]. 航空学报, 2011, 32(6): 1007-1014.

YANG Dang-guo, WU Ji-fei, LUO Xin-fu. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavity[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1007-1014. (in Chinese)

[16] 余培汛, 白俊强, 郭博智. 射流对空腔噪声抑制效果研究[J]. 计算力学学报, 2014, 31(5): 663-669.

YU Pei-xun, BAI Jun-qiang, GUO Bo-zhi. Suppression effect of jet flow on aerodynamic noise of cavity[J].Chinese Journal of Computational Mechanics, 2014, 31(5): 663-669. (in Chinese)

[17] Zhang Y, Arora N, Sun Y, et al. Suppression of cavity oscillations via three-dimensional steady blowing[C]∥45th AIAA Fluid Dynamics Conference. Dallas, TX, US: AIAA, 2015.

[18] 王一丁, 郭亮, 童明波, 等. 高速飞行器空腔脉动压力主动控制与非线性数值模拟[J]. 航空学报, 2015, 36(1): 213-222.

WANG Yi-ding, GUO Liang, TONG Ming-bo, et al. Active control and nonlinear numerical simulation for oscillating pressure of high-speed aircraft cavity[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 213-222. (in Chinese)

[19] 宁方立, 史红兵, 丘廉芳. 前缘高频振动对亚声速开式空腔内强噪声影响的数值研究[J]. 航空学报, 2015, 36(12): 3843-3852.

NING Fang-li, SHI Hong-bing, QIU Lian-fang. Numerical research of high frequency vibration effect on subsonic open cavity macro-noise[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3843-3852. (in Chinese)

[20] Blazek J. Computational fluid dynamics principles and applications[M]. Oxford, UK: Elsevier, 2005.

[21] Venkatakrishnan V.On the accuracy of limiters and convergence to steady state solutions[C]∥31st Aerospace Sciences Meeting. Reno, NV, US: AIAA, 1994.

[22] Shur M L, Spalart P R, Strelets M K. A hybrid RANS-LES approach with delayed-DES and wall-modeled LES capabilities[J]. International Heat and Fluid Flow, 2008, 29(6): 1638-1649.

[23] Menter F R. Two-equation eddy-viscosity turbulence modeling for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[24] Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[C]∥Proceedings of the 1st AFOSR International Conference on DNS/LES. Ruston, LA, US:Greyden Press, 1997:4-8.

[25] Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195.

[26] 张群峰, 闫盼盼, 黎军. 内埋式弹舱与弹体相互影响的精细模拟[J]. 兵工学报, 2016, 37(12):2366-2376.

ZHANG Qun-feng, YAN Pan-pan, LI Jun. Elaborate simulation of interaction effect between internal weapon bay and missile[J]. Acta Armamentarii, 2016, 37(12): 2366-2376. (in Chinese)

[27] Quirk J. A contribution to the great Riemann solver debate[J]. International Journal for Numerical Methods in Fluids, 1994, 18(2): 555-574.

[28] Aradag S, Knight D. Simulation of supersonic flow over a cavity[C]∥43rd AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV, US: AIAA, 2005.

[29] Henshaw M J C. M219 cavity case: verification and validation data for computational unsteady aerodynamics, RTO-TR-26 [R]. London, UK: QinetiQ, 2002.

[30] 熊红亮, 袁格. 可压缩自由剪切层纹影试验研究[J]. 流体力学实验与测量, 2003, 17(2):74-77.

XIONG Hong-liang, YUAN Ge. Flow visualization about a compressible shear flow[J]. Experiments and Measurement in Fluid Mechanics, 2003, 17(2):74-77. (in Chinese)