一种鲁棒自适应容积卡尔曼滤波方法及其在相对导航中的应用

张旭， 崔乃刚， 王小刚， 崔祜涛， 秦武韬

(哈尔滨工业大学 航天学院， 黑龙江 哈尔滨 150001)

0 引言

无人机协同编队作战技术无疑是近年来引人瞩目的高新技术之一。为使无人机之间保持特定的队形实现通信与协调控制，需要获得准确的相对速度及相对位置信息。目前扩展卡尔曼滤波(EKF)算法和无迹卡尔曼滤波(UKF)算法是解决相对导航问题的主要途径。EKF算法虽然广泛应用在非线性滤波中，但其存在一定的局限性，而UKF算法采用无迹变换对非线性概率密度分布进行近似，相比EKF求雅克比矩阵计算量大的明显不足，UKF算法收敛性好并能有效地改善滤波精度。为了更好地满足相对导航精度的要求，有必要研究工程实现更简单、精度更高的滤波算法。容积卡尔曼滤波(CKF)算法[1-2]是近年来提出的一种新型非线性滤波算法，CKF算法与UKF算法相比，都属于确定采样型滤波算法，但CKF算法估计精度更高，实时性更好。传统的CKF算法对于偏离真实概率分布的噪声是敏感的，特别是一些具有“厚尾”的分布更加会引起滤波器性能不稳定或影响估计精度。因此，一些学者将基于Huber的广义最大似然估计理论[3-7]应用到系统状态估计问题中。Huber技术是一种以混合l1/l2范数为代价函数的最优估计方法，对偏离假定高斯分布的噪声是鲁棒的，但如果这些假设的参数与真实分布偏离很大时，同样会导致滤波器有较大的误差，甚至会引起滤波发散。

为了能够在未知噪声分布特性的情况下提高滤波性能，并减小滤波发散的可能性，引入自适应技术[8-9]，与系统状态一起实时地在线估计噪声统计特性。目前，最常用的自适应状态估计方法是协方差匹配技术[10-11]，协方差匹配技术的核心思想是真实残差协方差矩阵和理论预测协方差矩阵是相匹配的，真实协方差是对有限长度滑动窗口内存储残差样本点实时估计而得到的。

很少有学者将鲁棒性估计与自适应算法结合起来进行状态估计，本文将基于Huber技术的CKF估计与利用残差序列实时估计、调整的自适应噪声统计特性估计两种思想结合起来，提出了一种带噪声估计器的鲁棒自适应CKF算法，并应用到无人机编队相对导航问题中。给出了编队无人机相对导航模型，针对测量噪声特性服从非高斯分布的情况，利用存储残差的样本均值和样本协方差估计测量噪声和过程噪声协方差矩阵的方法正好解决了鲁棒性的问题，最后进行了仿真研究，对比了该算法与标准CKF算法及鲁棒CKF算法的性能。

1 鲁棒CKF算法

考虑如下离散非线性系统：

xk+1=f(xk)+vk，

(1)

zk=h(xk)+wk，

(2)

式中：xk为k时刻的系统状态向量；zk为观测向量；系统过程噪声vk和量测噪声wk为互不相关的高斯白噪声序列，

(3)

Q为系统噪声方差阵，R为量测噪声方差阵，δkj为Kronecker-δ函数。

鲁棒 CKF滤波算法具体步骤如下：

1)初始化。

0=E[x0],
P0=E[(x0-0)(x0-0)T],

(4)

2)计算容积点。

Xi,k-1|k-1=Sk-1|k-1ξi+k-1|k-1,i=1,2,…,2n，

(5)

3)时间更新。

传播容积点：

(6)

状态一步预测值：

(7)

(8)

4)量测更新。

Cholesky因式分解：

(9)

计算用于量测更新的容积点：

Xi,k|k-1=Sk|k-1ξi+k|k-1.

(10)

传播容积点：

Zi,k|k-1=h(Xi,k|k-1).

(11)

量测的估计值为

(12)

协方差阵Pzz,k|k-1和互协方差阵Pxz,k|k-1分别为

(13)

(14)

预测误差δk为

δk=xk-k|k-1，

(15)

式中：xk为k时刻状态真实值；k|k-1为状态预测值，

k|k-1=xk-δk.

(16)

量测方程近似为

zk≈k|k-1+Hkδk，

(17)

式中：Hk=((Pk|k-1)-1Pxz,k|k-1)T.

量测更新问题转换为线性回归问题的求解：

(18)

定义下列变量：

(19)

(20)

(21)

(22)

则线性回归问题可转化为

(23)

鲁棒CKF滤波量测更新转化为求解代价函数的最小值：

(24)

式中：ζk,i为ζk的第i个分量，且ζk=Mkk|k-1-yk；m为ζk的维数；

(25)

γ为调节参数。ρ函数为最小l1、l2范数混合的形式。当γ→0时，ρ函数趋近于l1范数最小；当γ→∞时，ρ函数趋近于l2范数最小。利用ρ函数计算得到的估计值具有一定的鲁棒性。

代价函数J最小的解满足：

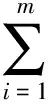
(26)

式中：φ(ζk,i)=ρ′(ζk,i). 定义函数ψ(ζk,i)和矩阵Ψ(ζk,i)分别为ψ(ζk,i)=φ(ζk,i)/ζk,i、Ψ(ζk,i)=diag[ψ(ζk,i)]，然后将ζk,i=(Mkk|k-1-yk)i代入(26)式得

(27)

(27)式的迭代解为

(28)

式中：c为迭代次数。

(29)

2 一种鲁棒自适应CKF方法

鲁棒 CKF滤波对非线性问题进行滤波估计具有独特的优点，而且能克服CKF存在的一系列问题。但针对鲁棒CKF滤波在实际姿态测量传感器测量噪声统计特性不确定的情况下导致滤波精度下降及非鲁棒性问题，本文基于协方差匹配技术[10-11]，利用鲁棒CKF滤波的残差序列，设计了一种在线估计噪声统计特性的鲁棒自适应CKF方法。

量测残差序列主要是生成量测噪声统计的估计值，状态预测残差主要是计算过程噪声统计的估计值，利用长度为N的滑动窗口缓存器对量测噪声和过程噪声残差进行存储，并对量测噪声和过程噪声的统计特性进行计算。量测噪声样本协方差矩阵为

(30)

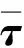
(31)

Cτ的期望值为

(32)

把(30)式代入到(32)式中，得到量测噪声协方差矩阵的估计值为

(33)

(34)

式中：

(35)

(36)

最后通过量测噪声和过程噪声的初值及存储残差数据利用(33)式和(36)式更新协方差估计。

在计算量测噪声和过程噪声协方差矩阵的过程中，采用遗忘加权参数对接收到的量测数据进行加权，其中最近接收到的量测数据获得较大的权值。滤波器通过(37)式和(38)式实现：

(37)

(38)

3 相对导航模型

本文考虑采用领航- 跟随模式的无人机双机编队控制策略。相对导航模型由相对姿态方程和相对质心运动方程两部分组成[12-14]。

3.1 相对姿态方程

采用欧拉轴/角(e1,e2,e3,θ)组成4元数表示姿态矩阵中的各元素：

(39)

式中：对于4元数q的分量，前三者称为4元数的矢量部分，后者称为标量部分。

僚机与长机之间的相对4元数qf|l表示为

(40)

式中：qf定义为僚机的姿态4元数；ql定义为长机的姿态4元数；符号⊗表示4元数乘法。

因此，僚机与长机之间的相对4元数满足：

(41)

(42)

(43)

式中：p=[q1q2q3]T.

陀螺的测量模型为

(44)

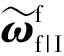
3.2 相对质心运动方程

(45)

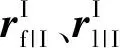
对(45)式求1阶导数、2阶导数分别为

(46)

(47)

由于

(48)

可得

(49)

加速度计的测量模型为

(50)

3.3 量测方程

视觉导航系统主要包括视觉导航相机和特征光点两部分，本文将视觉导航相机安装在长机上并将3个特征光点安置在僚机上，量测值即为长机与僚机之间的相对视线矢量。(Xi,Yi,Zi)T是特征光点在僚机上的位置，i=1,2,3. (x,y,z)T是无人机之间相对位置矢量的3个分量。其中，单位视线矢量定义为

(51)

式中：

(52)

4 仿真分析

4.1 仿真条件

1)惯导系统及滤波初始条件。仿真实验的初始条件如表1所示。

表1 仿真初始条件

2)特征光点位置。由相对导航系统的可观测性可知，至少需要3个特征光点，特征光点位置分布由表2给出。

表2 特征光点分布

3)视觉导航系统参数。视觉传感器测量误差来自混合的零均值高斯概率分布，受污染的噪声概率密度函数表达式为

(53)

式中：ω为概率密度函数的自变量；ε为污染率；σv为视觉传感器的测量噪声方差，σi为污染噪声方差，仿真中σv=3 500 μrad，σi=5σv.

4.2 仿真结果及分析

图1 相对姿态误差Fig.1 Relative attitude errors

本文提出的鲁棒自适应滤波方法估计得到的相对姿态误差、相对位置误差和相对速度误差如图1～图3所示。通过仿真结果可以看出该算法估计出的位置精度可以达到厘米级别，能够对系统过程噪声和量测噪声统计特性进行实时估计，具有估计精度高、收敛速度快的特点。图4给出了EKF算法、CKF算法、鲁棒CKF算法和鲁棒自适应CKF算法4种滤波算法估计得到的位置误差。采用这4种滤波算法求解得到的相对位置误差分别为4.861 7 cm、3.496 6 cm、1.613 7 cm和0.681 6 cm. 从图4可以看出，在视觉导航传感器量测噪声服从非高斯分布的情况下，鲁棒自适应CKF算法的估计精度比EKF算法、CKF算法和鲁棒CKF算法有显著的提升。

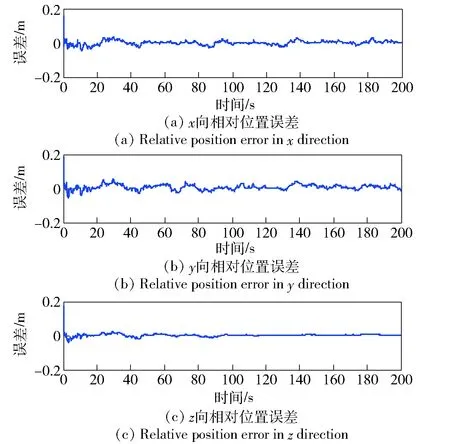
图2 相对位置误差Fig.2 Relative position errors

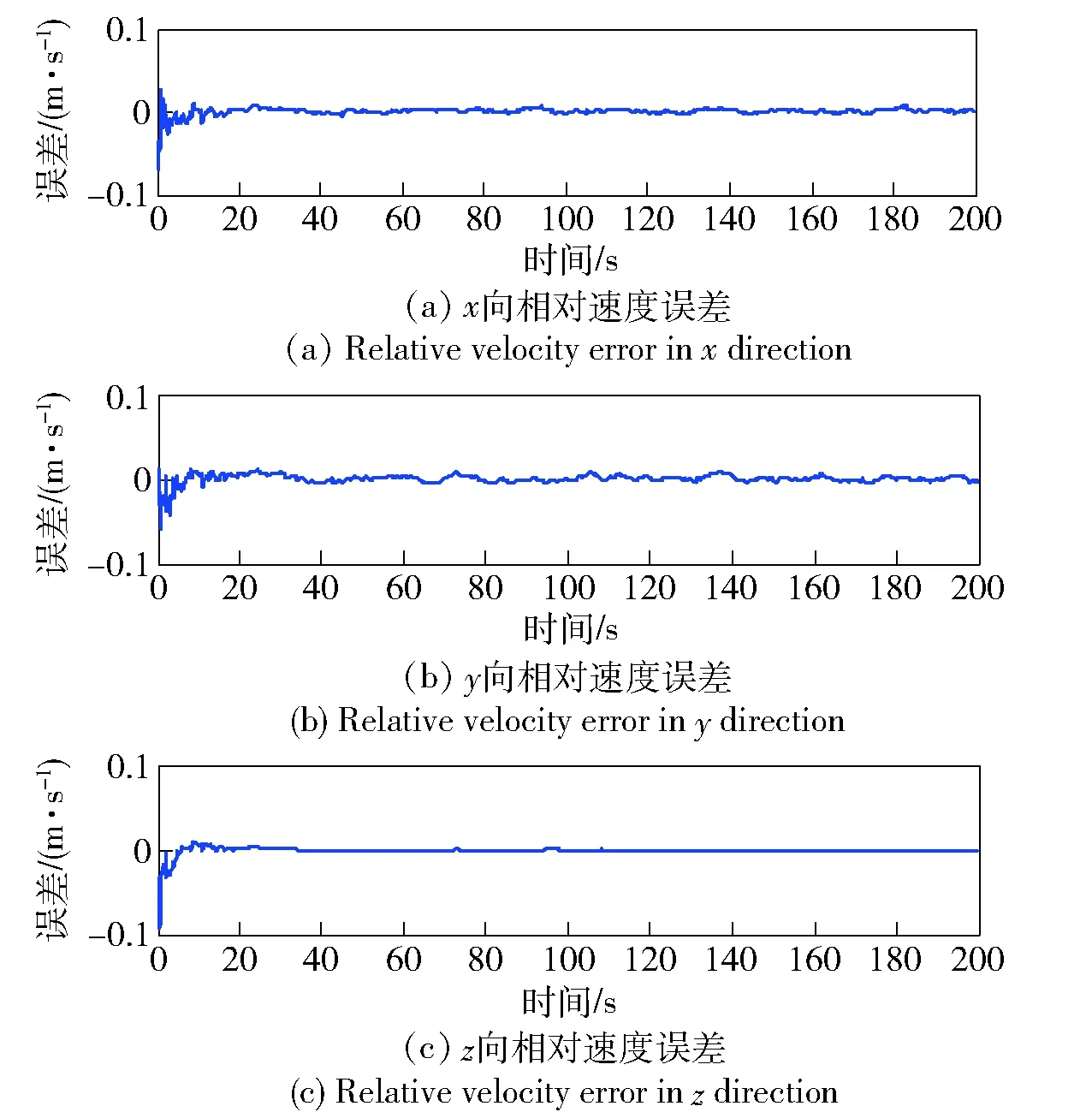
图3 相对速度误差Fig.3 Relative velocity errors

图4 4种滤波方法相对位置误差对比Fig.4 Comparation of relative position errors of four methods

5 结论

本文针对无人机编队相对导航系统中视觉传感器量测噪声服从非高斯分布的问题，提出一种混合鲁棒/自适应滤波方法，分析和仿真结果表明：

1) 利用Huber技术将标准CKF的量测更新步骤改为线性回归问题，对受污染的噪声有较强的鲁棒性。

2) 将基于Huber技术的鲁棒性估计与自适应噪声统计特性估计结合起来，提出了一种鲁棒自适应CKF算法，解决了无人机编队相对导航系统中视觉传感器量测噪声服从非高斯分布的问题。

3) 对比标准CKF算法和鲁棒CKF算法，提出的鲁棒自适应CKF算法对非高斯量测噪声具有较强的自适应性，能够获取更优的相对导航参数，且具有更强的鲁棒性。

)

[1] Wu H, Chen B F, Yang B F, et, al. Robust derivative-free cubature Kalman filter for bearings-only tracking[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(8):1865-1870.

[2] 孙枫, 唐李军. 基于 cubature Kalman filter的INS/GPS组合导航滤波算法[J]. 控制与决策, 2012, 27(7):1032-1036.

SUN Feng, TANG Li-jun. INS/GPS integrated navigation filter algorithm based on cubature Kalman filter[J]. Control and Decision, 2012, 27(7):1032-1036. (in Chinese)

[3] 黄玉, 武立华, 孙枫. 基于Huber M估计的鲁棒Cubature卡尔曼滤波算法[J]. 控制与决策, 2014, 29(3):572-576.

HUANG Yu, WU Li-hua, SUN Feng. Robust cubature Kalman filter based on Huber M estimator[J]. Control and Decision, 2014, 29(3):572-576. (in Chinese)

[4] 秦康, 董新民, 陈勇. 基于Huber的鲁棒高阶容积卡尔曼滤波算法[J]. 计算机工程与应用, 2017, 53(7):21-29.

QIN Kang, DONG Xin-min, CHEN Yong. Huber-based robust high-degree cubature Kalman filter algorithm[J]. Computer Engineering and Applications, 2017,53(7):21-29. (in Chinese)

[5] 王小刚, 路菲, 崔乃刚. Huber-based滤波及其在相对导航问题中的应用[J]. 控制与决策, 2014, 25(2):287-290.

WANG Xiao-gang, LU Fei, CUI Nai-gang. Huber-based filter and its application to relative navigation[J]. Control and Decision, 2014, 25(2):287-290. (in Chinese)

[6] 崔乃刚, 张龙, 王小刚, 等. 自适应高阶容积卡尔曼滤波在目标跟踪中的应用[J]. 航空学报, 2015, 36(12):3885-3895.

CUI Nai-gang, ZHANG Long, WANG Xiao-gang, et al. Application of adaptive high-degree cubature Kalman filter in target tracking[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12):3885-3895.(in Chinese)

[7] 高敬东, 李开龙, 常路宾. 基于Huber的改进鲁棒滤波算[J]. 系统仿真学报, 2014, 26(8):1769-1774.

GAO Jing-dong, LI Kai-long, CHANG Lu-bin. Huber-based modified robust filter algorithm[J]. Journal of System Simulation, 2014, 26(8):1769-1774. (in Chinese)

[8] 王洁, 熊智, 邢丽, 等. 基于新息自适应滤波的惯性测量单元误差在线标定方法研究[J]. 兵工学报, 2016, 37(7):1203-1213.

WANG Jie, XIONG Zhi, XING Li, et al. Online calibration of IMU errors of inertial navigation system based on innovation-based adaptive filtering[J]. Acta Armamentarii, 2016, 37(7):1203-1213. (in Chinese)

[9] 丁家琳, 肖建. 基于极大后验估计的自适应容积卡尔曼滤波器[J]. 控制与决策, 2014, 29(2):327- 334.

DING Jia-lin, XIAO Jian. Design of adaptive cubature Kalman filter based on maximum a posteriori estimation [J]. Control and Decision, 2014, 29(2):327-334. (in Chinese)

[10] Karlgaard C D, Schaub H. Adaptive nonlinear Huber-based navigation for rendezvous in elliptical orbit[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2):388-402.

[11] 于浛, 魏喜庆, 宋申民, 等. 基于自适应容积卡尔曼滤波的非合作航天器相对运动估计[J]. 航空学报, 2014, 35(8):2251-2260.

YU Han, WEI Xi-qing, SONG Shen-min, et al. Relative motion estimation of non-cooperative spacecraft based on adaptive CKF[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8):2251-2260. (in Chinese)

[12] 王小刚, 郭继峰, 崔乃刚. 一种鲁棒Sigma-point滤波算法及其在相对导航中的应用[J]. 航空学报, 2010, 31(5): 1024-1029.

WANG Xiao-gang, GUO Ji-feng, CUI Nai-gang. Robust sigma-point filtering and its application to relative navigation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5):1024-1029.(in Chinese)

[13] 王小刚. 非线性滤波方法在无人机相对导航上的应用[D]. 哈尔滨：哈尔滨工业大学, 2010:18-33.

WANG Xiao-gang. The application of nonlinear filtering to UAV relative navigation[D]. Harbin: Harbin Institute of Technology, 2010:18-33. (in Chinese)

[14] 曲法义, 王小刚, 崔乃刚, 等. 基于惯导/GPS/视觉的无人机容错相对导航方法[J]. 中国惯性技术学报, 2013, 21(6): 781-785.

QU Fa-yi, WANG Xiao-gang, CUI Nai-gang, et al. Fault-tolerance relative navigation approach based on SIN/GPS/Vision for UVA[J]. Journal of Inertial Technology, 2010, 21(6):781-785.(in Chinese)