水中聚能战斗部毁伤双层圆柱壳的数值模拟与试验研究

李兵， 刘念念， 陈高杰， 张阿漫

(1.91439部队， 辽宁 大连 116041； 2.哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001)

0 引言

为达到对目标高效毁伤的要求，采用定向战斗部技术和聚能战斗部技术是增大鱼雷作战威力现实可行的技术途径，聚能型战斗部成为水中兵器战斗部发展的重要方向[1]。目前，国内外对聚能战斗部方面的研究主要集中在聚能射流形成理论研究、药型罩设计研究[2-3]、数值仿真技术研究[4-6]等方面，对于潜艇的破坏分析多数简化为聚能战斗部对靶板的侵彻[7-8]，聚能战斗部毁伤试验以陆上水箱试验为主[1]，对目标的毁伤作用主要偏重于金属射流的毁伤特性研究，对聚能型战斗部的水下毁伤性能试验研究、聚能型战斗部水下作用规律和水下毁伤机理的研究相对较少。

本文基于光滑粒子流体动力学(SPH)- 有限元方法(FEM)耦合算法，从金属射流、爆炸冲击波载荷及气泡脉动载荷3个方面，对聚能射流形成过程及聚能战斗部对双层圆柱壳结构的毁伤过程进行分析，探索聚能战斗部水中兵器对双层壳舱段模型的毁伤特性，并进行了海上模型试验验证，旨在为聚能战斗部水中兵器毁伤威力的考核和评估提供有效的技术支持。

1 数值计算模型

1.1 计算模型

为计算模拟聚能战斗部对双层圆柱壳舱段结构的毁伤效应，建立了如图1所示的三维数值模型。其中聚能战斗部采用SPH[9-13]方法模拟，计算分析聚能装药的爆轰及金属射流的形成；而双层圆柱壳采用FEM建模与模拟；通过将SPH方法与FEM耦合，实现聚能战斗部水下爆炸对双层圆柱壳结构毁伤过程的数值模拟。高能炸药、药型罩和水离散成SPH粒子，聚能战斗部的计算模型如图2所示。

图1 聚能战斗部毁伤双层圆柱壳的SPH-FEM数值模型Fig.1 SPH-FEM numerical simulation model

图2 聚能战斗部模型Fig.2 Shaped charge warhead model

聚能战斗部的装药长度H为105 mm，装药直径D为81 mm，装药成分为：RDX占比80%，TNT占比20%；装药密度为1.740 g/cm3. 药型罩为半球形紫铜罩，厚度d为10 mm. 炸高为70 mm. 水域直径为600 mm，长度为1 500 mm.

双层圆柱壳舱段长2.5 m，非耐压壳直径2.2 m，耐压壳直径1.8 m，非耐压壳厚3.0 mm，耐压壳厚7.0 mm. 模型共3条环肋板，环肋板厚1.5 mm.

1.2 材料模型及参数

炸药爆轰产物采用Jones-Wilkins-Lee(JWL)状态方程[14]进行压力计算，各参数取值见表1[15].

(1)

式中：p为爆轰产物的压力；η为爆轰产物的相对比容，η=ρ/ρ0，ρ为材料当前密度，ρ0为材料初始密度；A、B、R1、R2和ω为与炸药状态有关的常数；e为材料当前内能。

表1 炸药JWL状态方程参数

金属材料和水采用Mie-Gruneisen状态方程[16]：

(2)

式中：Γ为Gruneisen常数；e0为材料初始内能；pH为冲击Hugoniot曲线上点的压力，

(3)

金属结构的强度在SPH近似中体现为偏应力张量τ，可通过金属的本构关系求得。

表2 不同材料Mie-Gruneisen状态方程中的参数

(4)

在更新应力时，为判断粒子当前是否处于塑性屈服状态[17]，采用von Mises屈服准则，偏应力分量修正后的表达式为

(5)

(6)

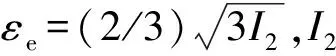
表3 金属材料Johnson-Cook模型参数

2 数值模拟结果

2.1 聚能射流形成过程

图3 射流速度等值线云图Fig.3 Velocity contours of jet

聚能装药在中心点起爆的情况下，球面爆轰波从起爆点开始向周围传播，在一段时间内波阵面到达药型罩的顶端，药型罩在波阵面的推动下开始压垮运动。由于爆轰波到达罩壁各部分的先后顺序不同，罩壁各部分依次运动进入对称轴线，并以对称轴线为中心，药型罩表面发生迅速碰撞和挤压变形，产生高速金属射流。

射流速度等值线云图如图3所示，射流在轴线处碰撞、挤压，头部速度增大至最大速度后减小。球面爆轰波阵面到达药型罩顶端后，药型罩发生压垮运动，爆轰波压力驱动半球罩继续不断翻转变形，整个罩体被压垮至轴线，射流速度达到峰值，此时半球罩的顶部金属内部已经被翻转到外面成为射流的头部，之后金属射流头部速度开始减小，金属射流继续拉长变细。

2.2 聚能射流对双层壳体结构的毁伤

2.2.1 侵彻速度衰减规律

图4 射流侵彻过程中速度云图Fig.4 Velocity contours of jet during penetrating

聚能战斗部对双层壳体结构的毁伤过程如图4所示。金属射流在速度梯度的推动下变细变长，先于爆轰产物到达非耐压壳，随后依次穿透非耐压壳、层间水及耐压壳。在40 μs时金属射流即将开始穿透非耐压壳，射流头部由于受到非耐压壳的作用而变得扁平；在48 μs时射流穿透非耐压壳，之后由于层间水的作用，射流头部出现削平现象，且射流头部发生径向飞散，径向飞散的射流分布在金属射流的四周，射流直径增大；在102 μs时金属射流开始穿透耐压壳，从图4中可以看出金属射流的尾部已经与爆轰产物融在一起；在120 μs时金属射流完全穿透耐压壳，射流头部完全被削平，径向飞散的射流径向直径比之前减小。

射流在侵彻壳体模型过程中最大速度不断减小，射流最大速度变化曲线如图5所示。由图5可知，射流头部速度随着时间的变化呈现缓慢减小趋势，最大速度约为3 834 m/s. 在44 μs时，曲线中切线斜率增大，即表示射流头部速度衰减速率变大，这是由于非耐压壳对射流的阻力作用；之后，射流头部速度随着层间水的作用逐渐减小，在92 μs时射流头部速度基本稳定，约为2 374 m/s；在124 μs时，射流在耐压壳的阻碍下，头部速度再次减小。通过对比切线斜率可知，射流在侵彻双层壳体舱段的过程中，非耐压壳、层间水及耐压壳均导致了射流速度的减小，非耐压壳对射流速度的影响较大，其次是层间水，最后是耐压壳。可见，射流在侵彻壳体、层间水及耐压壳的过程中，由于阻力使射流头部不断地消耗，头部速度呈下降趋势。

图5 金属射流侵彻速度随时间衰减曲线Fig.5 Penetrating velocity decay of metal jet

2.2.2 破口分析

图6 非耐压壳破口曲线Fig.6 Crevasse plot of non-pressure hull

聚能战斗部起爆后，金属射流开始作用于非耐压壳，非耐压壳被射流击穿形成破口，定义S为破口与炸药直径之比，图6为非耐压壳破口曲线。由曲线可知，金属射流使得非耐压壳产生初始破口，之后破口随着射流直径的增大而增大，随后破口大小趋于稳定，当射流直径增大到一定程度后，周边的空气和水随着射流穿透非耐压壳，使得破口直径突然增大，且破口直径大于射流直径。非耐压壳最终的破口云图如图7所示。因此，非耐压壳的破口是由射流、空气以及水共同作用引起的，射流导致初始破口，随后在空气和水的作用下，破口进一步扩大。

图7 非耐压壳破口云图Fig.7 Crevasse contour of non-pressure hull

耐压壳的破口曲线如图8所示，由曲线可知，金属射流使得耐压壳产生初始破口，破口尺寸明显小于非耐压壳破口，之后破口随着射流直径的增大而增大，且破口直径和射流直径一致，耐压壳最终的破口云图如图9所示。因此，耐压壳的破口主要是由射流作用引起的。

图8 耐压壳破口曲线Fig.8 Crevasse plot of pressure hull

图9 耐压壳破口云图Fig.9 Crevasse contour of pressure hull

总体来看，聚能战斗部形成的金属射流会造成壳体结构的局部小尺寸破口，且耐压壳的破口小于非耐压壳破口。其中，非耐压壳的破口主要由射流、空气、水以及炸药的作用引起，而耐压壳破口主要由金属射流引起。

2.3 冲击波及气泡载荷对双层壳体结构的毁伤

非耐压壳破口云图见图10所示。聚能战斗部起爆约0.1 ms后，产生的冲击波开始作用于非耐压壳迎爆面中部并形成初始破口，之后随着冲击波的不断传播，冲击波作用至圆柱壳两端横舱壁，再作用于非耐压壳的背爆面位置。在聚能射流引爆初期，随着冲击波的不断冲击，迎爆面的破口尺寸不断扩大，当爆轰产物膨胀一定时间后，随着冲击波与周围水介质的耦合作用及能量的扩散，破口尺寸不再发生变化，而非耐压壳体在气泡脉动和气泡射流的联合作用下，塑性凹陷区域不断扩大。在50.0 ms时刻，凹陷区域及破口尺寸不再变化。

非耐压壳破口曲线如图11所示。由图11可知，相较于金属射流造成的破口，冲击波及气泡载荷引起的破口尺寸要大很多。金属射流稳定后，非耐压壳的破口与炸药直径之比S≈0.772，而冲击波及气泡载荷引起的破口尺寸与炸药直径之比S≈2.771. 这是因为聚能射流引起的破口主要由金属射流、空气及水共同作用引起，其所引起的结构破口尺寸相对要小；而爆炸冲击波载荷及气泡载荷作用范围大，由此引起的结构破口尺寸较金属射流大。

图12 耐压壳破口云图Fig.12 Crevasse contours of pressure hull

图12为耐压壳破口云图，如图12所示，耐压壳在冲击波和气泡载荷的作用下并未有破口产生，但在迎爆面位置产生了大面积塑性凹陷。

3 试验验证

3.1 试验工况

聚能战斗部对双层壳体模型的海上实爆验证试验中的试验模型几何参数与仿真模型一致，战斗部接触爆炸，战斗部纵轴线与模型法线间夹角为0°.

3.2 试验结果分析

图13～图16为试验模型的毁伤情况，如图所示，在聚能装药载荷的作用下，模型非耐压壳体及耐压壳体均出现不同程度的毁伤。非耐压壳体迎爆面中部位置出现大面积塑性凹陷及局部裂纹，损伤发生在横跨连续多条肋骨的较大范围内，如图13所示；非耐压壳表面中心位置处形成小尺寸穿孔，如图14所示，且穿孔周围有毛刺现象产生；耐压壳体迎爆面中部出现塑性凹陷，并在穿孔位置处撕裂形成大尺寸裂纹，如图15所示，且从图中可明显看出，壳体是在射流侵彻破口后发生了撕裂变形；此外，金属射流穿透舱段模型，在耐压壳背爆面产生穿孔，如图16所示。

图13 非耐压壳外部整体破坏情况Fig.13 Damage of non-pressure hull

图14 非耐压壳外部穿孔Fig.14 Perforation of non-pressure hull

图15 耐压壳内部迎爆面破坏情况Fig.15 Front side damage of pressure hull

图16 耐压壳背爆面穿孔Fig.16 Back side perforation of pressure hull

此外，从试验结果和模型结构还可分析得出，双层圆柱壳模型的环肋板、T型加强材焊缝处为结构薄弱部位。这是由于环肋板附近在加强筋的支撑作用下会产生较高的结构抗力，成为高应力区，而钢板焊缝处是结构容易开裂的薄弱部位。

3.3 试验与仿真结果对比

非耐压壳毁伤数值模拟结果如图17所示。对比图13可知，模型迎爆面位置均出现大面积塑性凹陷，凹陷面积相当；且模型环肋板位置均产生一条大尺寸裂纹，裂纹发生的位置和尺寸吻合良好。

图17 非耐压壳毁伤模拟结果Fig.17 Simulation of non-pressure hull damage

在模型试验和数值模拟结果中，耐压壳在聚能射流作用下均出现小尺寸穿孔，穿孔尺寸的试验值为69 mm，数值模拟值为50.38 mm，与试验结果的相对误差为27.02%，满足工程要求。

4 结论

本文基于SPH-FEM数值模拟算法，模拟了水中聚能战斗部对双层圆柱壳体结构的毁伤过程，分析了高速金属射流、强冲击波与气泡载荷联合作用下对双层圆柱壳体结构的毁伤模式和毁伤特性，并进行了海上模型试验验证，得出以下结论：

1)SPH-FEM数值方法与试验结果吻合良好，证明了SPH-FEM方法在模拟三维工程问题时的有效性和可行性。

2)水中聚能战斗部对双层圆柱壳结构的破坏载荷主要有3种：金属射流、冲击波载荷及气泡载荷。其中，金属射流穿透力强，造成结构的局部小尺寸破口；冲击波载荷及气泡载荷作用面积大，引起结构的大面积破口及塑性凹陷。

)

[1] 郭涛, 吴亚军. 鱼雷战斗部技术研究现状及发展趋势 [J] . 鱼雷技术, 2012, 20(1): 74-77.

GUO Tao, WU Ya-jun. Perspective of the technologies about torpedo warhead[J] . Torpedo Technology, 2012, 20(1): 74-77.(in Chinese)

[2] Chou P C, Flis W J. Recent development in shaped charge technology[J]. Propellants, Explosives, Pyrotechnics, 1986, 11(4):99-114.

[3] 徐斌, 刘春美, 黄广炎. 基于正交试验法研究线型聚能装药结构对双层靶板的作用[J]. 科学技术与工程, 2015, 15(35):138-143.

XU Bin, LIU Chun-mei, HUANG Guang-yan. Study on linear shaped charge jet penetrating into double layer targets based on orthogonal optimization method[J] . Science Technology and Engineering, 2015,15(35):138-143.(in Chinese)

[4] Zhang A M, Yang W S, Huang C, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Computers & Fluids, 2013, 71(3): 169-178.

[5] 李金明, 刘波, 姚志敏. 基于LS-DYNA程序的聚能装药数值仿真研究[J]. 计算机与数字工程, 2016, 44(2): 218-222.

LI Jin-ming, LIU Bo, YAO Zhi-min. Shaped charge numerical simulation based on LS-DYNA program[J]. Computure & Digital Engineering, 2016, 44(2): 218-222.(in Chinese)

[6] 李兵, 张之凡, 明付仁, 等. 聚能战斗部对潜艇舱段结构毁伤特性研究[J]. 兵工学报, 2014, 35(2):362-365.

LI Bing, ZHANG Zhi-fan, MING Fu-ren, et al. Research on damage characteristics of submarine cabin subjected to shaped charge warhead[J]. Acta Armamentarii, 2014, 35(2):362-365.(in Chinese)

[7] 李磊, 马宏昊, 沈兆武, 等. 聚能射流侵彻钢靶的SPH-FEM 数值模拟[J]. 南京理工大学学报, 2013, 37(2):226-232.

LI Lei, MA Hong-hao, SHEN Zhao-wu, et al. Numerical simulation of shaped charge jet perforating steel target by SPH-FEM coupling method[J]. Journal of Nanjing University of Science and Technology, 2013, 37(2):226-232.(in Chinese)

[8] 郭刘伟, 曹仁义, 庞勇, 等. 聚能射流水中侵彻行为的实验研究[J]. 实验力学, 2015, 30(1):111-115.

GUO Liu-wei, CAO Ren-yi, PANG Yong, et al. Experimental investigation on water penetration behavior of shaped charge jet[J]. Journal of Experimental Mechanics, 2015, 30(1):111-115.(in Chinese)

[9] 杨刚, 傅奕珂, 郑建民, 等. 基于SPH 方法对不同药型罩线性聚能射流形成及后效侵彻过程的模拟[J]. 振动与冲击, 2016, 35(4):56-61.

YANG Gang, FU Yi-ke, ZHENG Jian-min, et al. Simulation of formation and subsequent penetration process of linear shaped charge jets with different liners based on SPH method[J]. Journal of Vibration and Shock, 2016, 35(4):56-61.(in Chinese)

[10] Chen J K, Beraun J E. A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems[J]. Computer Method in Applied Mechanics Engineering, 2000, 190(1/2): 225-239.

[11] 李磊, 沈兆武, 李学岭. SPH方法在聚能装药射流三维数值模拟中的应用[J]. 爆炸与冲击, 2012, 32(3):316-321.

LI Lei, SHEN Zhao-wu, LI Xue-ling. Application of SPH method to numerical simulation of shaped charge jet[J]. Explosion and Shock Waves, 2012, 32(3):316-321.(in Chinese)

[12] Attaway S, Heinstein M, Swegle J. Coupling of smoothed particle hydrodynamics with the finite element method[J]. Nuclear Engineering Design, 1994, 150(2/3): 199-205.

[13] Johnson G R, Stryk R A, Beissel S R, et al. An algorithm to automatically convert distorted finite elements into meshless particle during dynamics deformation[J]. International Journal of Impact Engineering, 2002, 27(10):997-1013.

[14] Dobratz B M. LLNL explosive handbook[M]. Livermore, CA, US: Lawrence Livemore National Laborary, 1985.

[15] Shin Y S, Lee M, Lam K Y , et al. Modeling mitigation effects of water shield on shock waves[J]. Shock and Vibration, 1998, 5(4):225-234.

[16] Libersky L D, Randles P W, Carney T C, et al. High strain Lagrangian hydrodynamics: a three-dimensional SPH code for dynamic material response[J]. Journal of Computational Physics,1993,109(6): 67-75.

[17] Steinberg D J. Spherical explosions and the equation of state of water[M]. Livermore, CA , US:Lawrence Livermore National Laboratory, 1987.