考虑导弹1阶驾驶仪的近似最小加速度峰值导引律

郭琨， 杨树兴

(北京理工大学 宇航学院， 北京 100081)

0 引言

随着制导武器的快速发展以及现代战争对其性能要求的日益提高，攻击角度约束在精确打击任务中日益常见。然而，制导火箭弹和静稳定度较高的的导弹因末端恢复力矩过大，而使操纵能力严重受限，可用过载偏小[1]，难以在现有制导控制方法下兼顾落点和落角的高精度要求。因此，亟须研究如何在满足大落角约束条件下，降低需用法向加速度(即法向加速度峰值)的制导控制方法。

最小化加速度峰值问题为一种最大值最小化问题。这类问题的研究集中于20世纪八九十年代，通常先将其转化为常规最优控制问题[2-3]，并推导出最优解的必要条件[4-7]，再用数值方法求解两点或多点边值问题[8-9]。然而这套方法因数值计算量庞大，而不便于弹上实时解算。文献[10]针对最小化加速度峰值问题，基于非线性模型证明了当不考虑系统惯性环节时，加速度峰值最小的导引律为解析的圆弧- 直线导引律(CLGL)。但是，当系统存在惯性环节时，CLGL将产生终端误差甚至失效，目前只能用数值方法，如近十年发展起来的高斯伪谱法[11]得到该问题的最优解。

在带落角约束的导引律研究领域中，最常见的方法为基于比例导引律[12-14]、基于最优控制方法[15-20]、基于自适应控制[21]、滑模控制和反步控制[22-24]等方法设计导引律，这些方法虽然各有不同的优势，但在兼顾考虑系统惯性、非线性以及解的最优性上，依然有难度。如基于最优控制方法设计导引律时，为得到解析形式的解，通常要忽略自动驾驶仪的惯性或采用线性化模型，而其他几种方法并不具备最优性。多项式导引律(PGL)[25]是在同时忽略自动驾驶仪惯性和线性化模型的基础上，得到解析形式的导引律，当其作用于1阶惯性系统时，控制指令会出现振荡发散[26]。不过PGL有一个特性：在某些初始条件下，峰值加速度会出现在初始时刻，此性质便于通过控制初始加速度值来控制全导引过程中的加速度幅值。

此外，还有基于某种几何曲线设计的导引律，而此类方法中又以圆弧类导引律为多见。文献[27]为保证弹道在一定时间内收敛到圆弧轨迹上，在增益为2的比例导引律基础上加入了线性的角度偏差修正项，但此种方法容易在导引初始阶段产生较大的过载。文献[28]基于追踪法和圆弧导引，设计了布撒器的组合导引律，通过根据布撒器的可用过载来设置追踪法导引段的导引系数，以降低后面圆弧段的需用过载。文献[29]在研究水下侧向垂直攻击问题时，为了增加导弹对动力学滞后和目标机动的鲁棒性，在圆弧加直线的导引策略中引入捕获带宽概念，若导弹初始不在捕获带宽中，则以最大加速度(可用过载)做反向圆弧机动。文献[30-31]针对带终端角度约束的再入飞行器末制导问题，分别设计了二维和三维的圆轨迹制导律，通过定义两个圆轨迹跟踪误差矢量(一个速度方向误差，一个向心力误差)，缩短了飞行轨迹，减小了速度损失。文献[32]沿着标称的圆形弹道对导弹运动模型进行线性化，进而设计了二次型最优导引律，仿真算例显示，即使实际弹道偏离标称弹道较远也能实现较高的落角精度。以上研究均没有主动加入对系统惯性环节的补偿，且文献[28-29]需提前知道可用过载，文献[28, 30, 31]均需要根据经验，提前调节出合适的导引系数。综上所述，国内外关于带落角约束的导引律均未涉及最小化加速度峰值问题，而关于圆弧类导引律的研究较少考虑系统的惯性，在一定程度上限制了其在末端可用加速度受限弹药上的应用。

本文在CLGL的基础上提出了一种同时考虑系统惯性和非线性的解析形式且加速度峰值近似最小的导引律。通过将CLGL的末段替换为一种改进的带1阶惯性补偿项的PGL(CPGL)，形成组合导引律(CL-CPGL)。通过切换点的设计，使CPGL部分既能修正终端位置和角度误差，又能保证切换点后的加速度幅值不超过切换点处，从而实现了CL-CPGL的有效性及近似最优性。

1 问题描述和研究回顾

1.1 问题描述

已知导弹飞行末段的初始位置和速度方向，导引导弹以一定角度攻击地面固定目标，使得弹道上的最大法向加速度最小，几何关系如图1所示。X0(x0,y0)和Xf(xf,yf)分别为导弹初始位置和终点位置，下标0和f分别表示初始和终端时刻；vM为导弹速度矢量，an为导弹法向加速度矢量(包含重力加速度)；规定坐标轴Oy与终点速度约束vM(tf)反方向平行；θ和σ分别为速度矢量、弹目视线与Oy轴的夹角(逆时针方向为正，0≤θ0<π，0≤σ0<π/2，θf=σf=0)。假设弹道只向一侧弯曲即an(t)≤0 m/s2，且导弹速度恒定，则该优化问题的数学表达式为

(1)

式中：θ0、θf、x0、xf、y0、yf为固定常数；u为控制指令；τ为1阶惯性常数。

图1 平面几何关系图Fig.1 Planar engagement geometry

1.2 CLGL简介

对无惯性环节系统，控制指令u(t)=an(t)，问题(1)式可通过引入1个辅助状态xa=const>0(下标a表示辅助变量)和1个路径约束-xa(t)≤an(t)≤0将目标函数转化为Mayer型：J=xa(tf). 记协态为λ=[λθ,λx,λy,λa]T，则哈密尔顿函数为

(2)

系统正则方程为

(3)

(4)

横截条件为

(5)

由极大值原理有

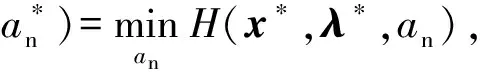
(6)

根据文献[10]可知，以上必要条件可推导出无惯性环节系统的解析最优解u*(t)，其所对应的最优弹道根据初始角度关系，有以下3种情况(见图2)：当θ0>2σ0时为圆弧- 直线(CL型)；当θ0=2σ0时为圆弧(C型)；当θ0<2σ0时为直线- 圆弧(LC型)。综合各圆弧和直线导引段上的角度关系，可得到无惯性系统加速度峰值最小的导引律，记为CLGL：

(7)

图2 无惯性系统3种初始几何关系下加速度峰值最小的弹道Fig.2 Minimax acceleration trajectories of lag-free systems under three initial geometry conditions

而实际的导弹自动驾驶仪存在动力学滞后，通常用1阶惯性环节来近似，即

(8)

此时，加速度峰值最小问题不存在解析解，在转化为常规最优控制问题后可用数值优化方法求解，但不便于弹上实时解算。因此，本文尝试推导一种近似最优的解析解。

2 1阶惯性环节对CLGL导引的影响

本节将分析1阶惯性环节对CLGL导引的影响，为后续导引律改进及证明提供依据。

2.1 圆弧段的收敛性

在圆弧段上，控制指令为

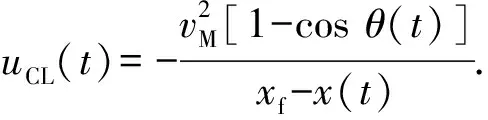
(9)

令aΔ(t)≜uCL(t)-an(t)，则

(10)

式中：方括号项的符号决定了aΔ(t)收敛与否。当θ0比σ0足够大，且an(t)向uCL(t)收敛时，方括号项为负，记为

(11)

式中：c为一个正常数。因此(10)式的解满足：

|aΔ(t)|<|aΔ(0)|e-ct，

(12)

即aΔ(t)按指数收敛至0. 可见，可通过圆弧段自身的收敛能力消除圆弧段初始时an(t)与uCL(t)的误差。这一性质将为后续CL-CPGL的设计提供一个假设依据。

2.2 惯性环节对弹道的影响

2.2.1 控制指令增大

(9)式对时间求导可得

(13)

2.2.2 弹道结构改变

在1阶惯性环节的影响下，C型和LC型最优轨迹分别演化为CL型和直线- 圆弧- 直线(LCL型)轨迹。为避免繁琐的求导，此处借助几何关系来证明。

先定义两个圆弧，如图3所示：C*(t)为当前最优弹道上的圆弧，其半径r*(t)为

(14)

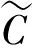
(15)

式中：d为弹目距离。结合(9)式、(14)式和(15)式可得到一对等价关系：

R(t)>r*(t)⟺θ(t)>2σ(t).

(16)

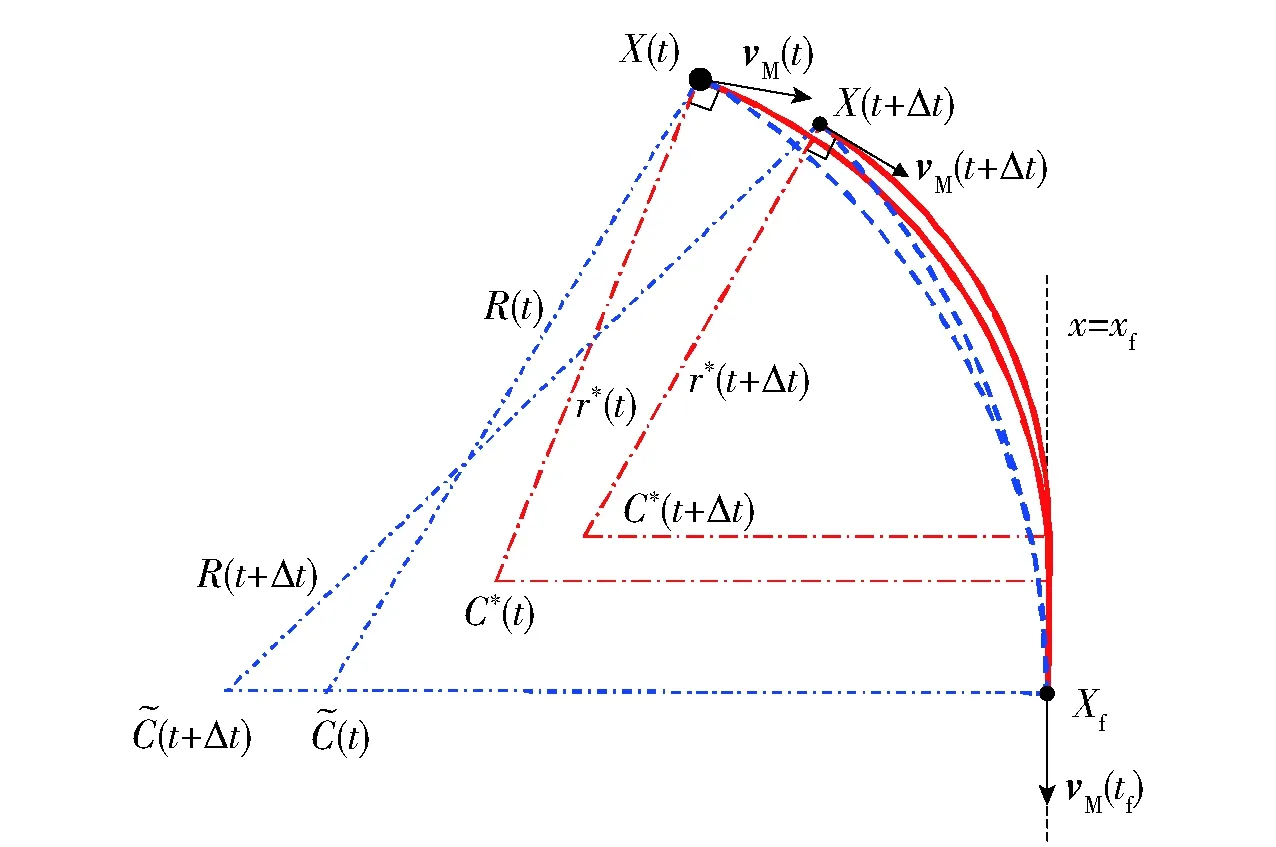
图3 圆弧导引段上C*(t)和变化示意图Fig.3 Changes in C*(t) and (t) on the circular arc guidance phase

3 CL-CPGL设计

基于第2节的分析，本节将对CLGL尾部的直线导引段进行改进，使其既能修正终点位置和角度误差，又能保持CLGL前段已经出现的最大加速度值，即改进段不增大加速度峰值。

PGL是针对线性无惯性系统设计的一种落角约束导引律，具有加速度峰值出现在初始时刻的良好特性，但文献[13]关于此性质的证明仅限于初始几何关系为情况A(见图4)，而本文的初始情况为情况B，因此需要重新证明此性质。另外须对PGL进行惯性补偿，以消除其作用于1阶惯性系统时所产生的振荡发散现象。

图4 文献[13]与本文分别对应的初始几何关系图Fig.4 Schematic diagram of two initial homing conditions in Ref.[13] and the present paper

基于以上分析，本节将CLGL尾部的直线导引段替换为CPGL导引段，形成CL-CPGL，并对其特性进行证明。

CLGL和CPGL分别是在非线性模型和线性模型下推导的，但由于CL-CPGL在切换时刻角度较小，自动满足CPGL的线性假设需求，所以CL-CPGL不受初始小角度的限制。

3.1 CL-CPGL表达式

切换条件为

(17)

式中：θ(t)≥2σ(t)表示在圆弧导引段上。组合导引律的表达式为

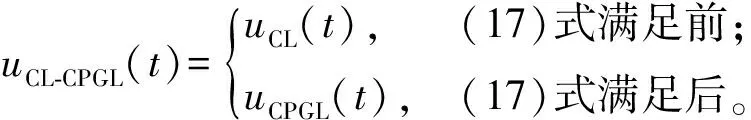
(18)

式中：

(19)

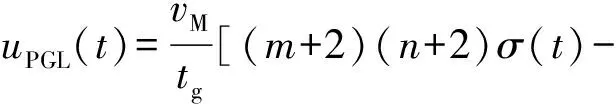
(20)

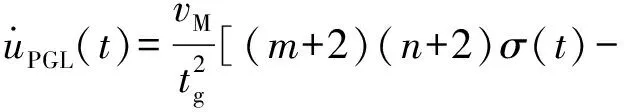
(21)

tg为剩余时间，tg=tf-t，tf的估算方法见文献[13]，m和n为导引常数，n>m≥0.

3.2 CL-CPGL的有效性证明

3.2.1 切换点的存在性

定理1CL-CPGL必以CPGL结束，即切换条件一定会满足。

证明1根据2.1节的分析，可认为an(t)在圆弧段上收敛足够快，在切换条件(17)式满足时，an(t)已收敛，即an(t)=uCL(t)，所以(17)式可以重写为

(22)

1)证明条件(22)式能够成立等价于存在时间ts，使得

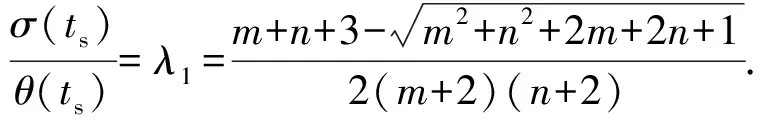
(23)

记rσθ≜σ(ts)/θ(ts)，将(20)式和sin (θ(ts))≈θ(ts)代入(22)式，化简后可得

rσθ[rσθ(m+2)(n+2)-(m+n+3)]=0,

(24)

此一元二次方程的两个根为

(25)

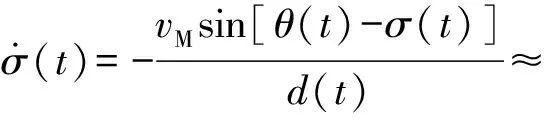
(26)

θ(t)的1阶导数为

(27)

将(26)式和(27)式代入(21)式可得

(28)

另一方面，

(29)

②分析λ1的取值范围。根据(23)式可知，λ1与m和n都负相关，其中当m=0且n=1时，λ1取到最大值1/6；当m→∞且n→∞时，λ1取到最小值0. 所以λ1的取值在区间(0,1/6]上。

综合σ(t)/θ(t)和λ1的取值范围，当θ0≤2σ0时，σ(t)/θ(t)在圆弧段上从1/2单调递减到0，覆盖区间(0,1/6]，所以一定存在某个时刻ts，使σ(t)/θ(t)=λ1；当θ0>2σ0时，σ(t)/θ(t)从σ0/θ0单调递减到0，若θ0/σ0<6，σ(t)/θ(t)的变化范围可覆盖区间(0,1/6]，若θ0/σ0≥6，则可以通过设置较大的m和n使λ1≤σ0/θ0，从而使ts存在。

综上，CL-CPGL能够保证切换点存在，以CPGL结束导引。证毕。

3.2.2 CPGL导引段的有效性

定理2CPGL导引段满足终端约束且不增加加速度峰值。

证明2为方便描述，先定义两个系统：系统Ⅰ为以切换点为起点的无惯性环节系统，系统Ⅱ为以切换点为起点的1阶惯性环节系统，即这两个系统都满足：

(30)

则CPGL的有效性可通过先证明PGL的有效性，再证明CPGL对系统Ⅰ的作用等效于PGL对系统Ⅱ的作用而得到。

1)用PGL导引系统Ⅰ，加速度峰值出现在初始时刻。

将文献[13]中系统动态方程的两个状态变量替换为

(31)

则uPGL(t)的闭合形式为

(32)

式中：

(33)

(34)

将(34)式代入(33)式可得

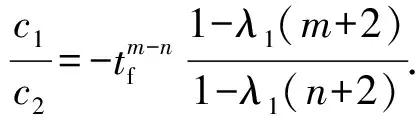
(35)

(36)

将(35)式代入(36)式可得

(37)

结合λ1的取值可得

(38)

(39)

而对于无惯性系统，an(t)=uPGL(t)，可得

(40)

因此用PGL导引系统Ⅰ时，加速度峰值出现在初始时刻。

2)系统Ⅱ在CPGL导引下产生的加速度an2(t)与系统Ⅰ在PGL导引下产生的加速度an1(t)相等。

在初始时刻，

an2(0)=an1(0)=uPGL(0)，

(41)

an2(t)对于时间的1阶导数为

(42)

an1(t)=an2(t),t≥0.

(43)

因此，若从组合导引律切换点起执行CPGL控制指令，可使1阶惯性系统的表现等同于PGL作用下无惯性系统的表现，从而满足终端约束，且保证加速度最大值出现在切换点。证毕。

综合定理1和定理2可知，CL-CPGL会在圆弧导引结束前将切换至CPGL导引，且在切换点处已取得加速度峰值，并满足终点位置、角度约束。

4 仿真验证

4.1 CLGL对1阶惯性系统的仿真验证

对3种典型的初始情况进行仿真，验证1阶惯性系统下CLGL的导引效果，各变量取值如表1所示，仿真结果如图5和表2所示。从图5(b)可见，加速度和控制指令可以在有限的一小段时间内收敛；收敛过程中，控制指令会稍微增大；3种情况都以一段零控制指令结束导引，其中θ0=72°的直线导引段最长，导致表2中θ0=72°时的角度误差和位置误差最大。以上现象验证了第2节的推断，并说明CLGL导引律对1阶惯性系统的不佳表现主要由末尾的直线导引段造成。

表1 初始条件1

图5 CLGL对1阶惯性系统的仿真结果Fig.5 Simulated results of CLGL for first-order lag system

表2 CLGL终端误差

4.2 组合导引律CL-CPGL对1阶惯性系统的仿真验证

图6 CL-CPGL对θ0=2.4σ0的仿真结果Fig.6 Simulated results of CL-CPGL for θ0=2.4σ0

初始条件仍如表1所示，初始加速度为0，导引常数取m=1、n=2. 图6～图8展示了3种初始情况即θ0为2.4σ0、2σ0、1.6σ0下的导引结果。从图6(b)、7(b)和8(b)中可以看出，在圆弧段收敛后，uPGL会两次穿越加速度曲线；当uPGL从下往上穿越时，uCL-CPGL有一个跳跃切换。切换点之后，加速度绝对值不再超过此处取值。此外，an(t)在末尾会有一小段时间大于0，此时弹道往反方向弯曲，如图6(a)、7(a)和8(a)所示。由此可见，CPGL在局部牺牲了单侧弯曲特性来保证加速度峰值出现在它的起点，即CL-CPGL的切换点；同时CL-CPGL可以满足1阶惯性系统的终点位置和角度约束。

图7 CL-CPGL对θ0=2σ0的仿真结果Fig.7 Simulated results of CL-CPGL for θ0=2σ0

图8 CL-CPGL对θ0=1.6σ0的仿真结果Fig.8 Simulated results of CL-CPGL for θ0=1.6σ0

4.3 组合导引律CL-CPGL与数值最优解的比较

为了检验CL-CPGL的优化效果，将其与1阶惯性系统的最优数值解进行比较。借助高斯伪谱法的软件包GPOPS计算出两种约束下的最优解：一种为单侧弯曲约束(u(t)≤0,an(t)≤0)下的解；另一种为双侧弯曲(控制指令和加速度的上界分别取CL-CPGL对应的值)约束下的解。 从图9可以看出，CL-CPGL的加速度峰值与GPOPS双侧弯曲约束下计算结果很接近，优于GPOPS单侧弯曲约束下计算结果，验证了CL-CPGL的近最优性。

图9 CL-CPGL和GPOPS数值解的比较Fig.9 Comparison of the numerical solutions by CL-CPGL and GPOPS

4.4 组合导引律末段CPGL对1阶惯性系统的仿真验证

为进一步验证定理2中CL-CPGL的性质，本节选取4.2节中θ0=2.4σ0情况下的切换点作为初始点(见表3)，对CPGL和PGL进行比较以验证它们分别作用于1阶惯性环节系统与无惯性环节系统时的等效性；另外分别改变初始角度θ0和导引律常数m、n，以进一步验证CPGL的加速度峰值出现在切换点的特性。

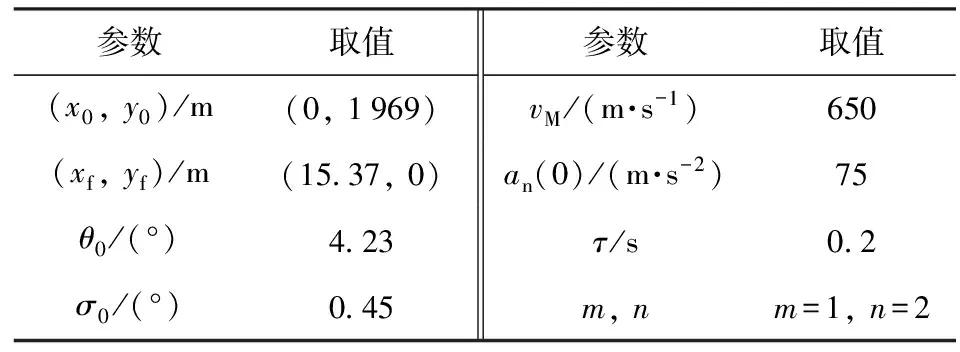
表3 初始条件2

4.4.1 PGL和CPGL的比较

从图10可以看出，CPGL作用于1阶惯性系统与PGL作用于理想系统产生的加速度(蓝实线和红圈)重合，最大幅值出现在初始时刻。而PGL作用于1阶惯性系统产生的加速度曲线(绿实线)会振荡，且在终点处发散。

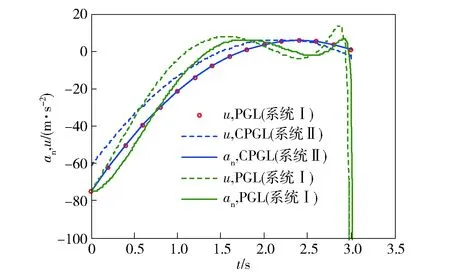
图10 CPGL和PGL的比较Fig.10 Comparisons of CPGL and PGL

4.4.2 CPGL的在不同切换角度和导引常数下的仿真

导弹初始位置、速度和时间常数由表3确定后，其他值可由θ0、m和n确定：由(20)式和(23)式可算出σ(ts)/θ(ts)，进而得到σ0和xf，再根据(22)式算出an(0). 此处未考虑其他独立变量vM和y0的影响是因为它们仅会让加速度曲线横向或纵向伸缩，并不影响加速度峰值出现的位置。

图11展示了在m=1、n=2时，即使θ0增大到90°，加速度峰值依然出现在初始时刻。因此，虽然“组合导引律加速度峰值出现在切换点”是在小角度假设下推导的，但在大角度下依然成立。

图11 不同导引常数下CPGL对1阶惯性系统的加速度曲线Fig.11 Acceleration profiles of CPGL for first-order lag system under different guidance gains

图12展示了在θ0=5°时，不同m、n取值下的加速度曲线。可以看出，m、n取值越大，加速度曲线越弯曲，加速度峰值也越容易出现在初始时刻。

图12 不同速度角下CPGL对1阶惯性系统的加速度曲线Fig.12 Accelerations of CPGL for first-order lag system at different initial velocity angles

5 结论

本文首先分析了驾驶仪1阶惯性滞后对加速度峰值最小导引律——CLGL导引效果的影响。在此基础上，提出一种带1阶惯性补偿能力解析形式的组合导引律，给出了其证明，并进行了仿真验证。主要结论如下：

1) 将无惯性系统假设下的CLGL用于1阶惯性系统时，3种初始几何条件下的弹道都变为以直线导引段结束；圆弧段能在短时间内收敛，其对加速度峰值增大的影响较小，可以忽略；而末尾的直线段不具备误差补偿能力，须对其改进。

2) 组合导引律以CLGL开始，必会在某一时刻满足切换条件，切换成1阶CPGL，直到导引结束。

3) 通过合理设计切换点以及对PGL进行惯性补偿，充分利用了CLGL和PGL的优点，使组合导引律既具备前者优化加速度峰值的能力，又具备后者满足落角约束、且保持加速度峰值不增大的能力。与数值最优解的仿真比较验证了组合导引律的近最优性。

4) 原有PGL“加速度峰值出现在初始时刻”所需的初始角度条件可扩展到更广的情况，满足本文组合导引律的导引场景。对切换点之后改进导引律的进一步仿真显示，即使增大切换角度或改变导引常数，改进部分依然保持加速度最大值出现在切换时刻的特性。说明考虑1阶惯性环节的组合导引律同样适用于大初始偏离角的情形。

)

[1] 杨树兴. 陆军多管火箭武器的发展与思考[J]. 兵工学报, 2016, 37(7):1299-1305.

YANG Shu-xing. Progress and key points for guidance of multiple launch rocket systems[J]. Acta Armamentarii, 2016, 37(7):1299-1305.(in Chinese)

[2] Warga J. Minimizing variational curves restricted to a preassigned set[J]. Transactions on the American Mathematical Society, 1964, 112(3):432-455.

[3] Miele A, Mohanty B P, Venkataraman P, et al. Numerical solution of minimax problems of optimal control, part 1[J]. Journal of Optimization Theory & Applications, 1982, 38(1):97-109.

[4] Powers W F. A Chebyshev minimax technique oriented to aerospace trajectory optimization problems[J]. AIAA Journal, 1972, 10(10): 1291-1296.

[5] Lu P, Vinh N X. Optimal control problems with maximum functional [J]. Journal of Guidance Control, and Dynamics, 1991, 14(6):1215-1223.

[6] Arutyunov A V, Silin D B, Zerkalov L G. Maximum principle and second-order conditions for minimax problems of optimal control[J]. Journal of Optimization Theory & Applications, 1992, 75(3):521-533.

[7] Bulirsch R, Montrone F, Pesch H J. Abort landing in the presence of windshear as a minimax optimal control problem. Part 1: necessary conditions[J]. Journal of Optimization Theory & Applications, 1991, 70(1):1-23.

[8] Oberle H J. Numerical treatment of minimax optimal control problems with application to reentry flight path problem[J]. Journal of the Astronautical Sciences, 1988, 36(1/2):159-178.

[9] Bulirsch R, Montrone F, Pesch H J. Abort landing in the presence of windshear as a minimax optimal control problem. Part 2: multiple shooting and homotopy[J]. Journal of Optimization Theory & Applications, 1991, 70(2):223-254.

[10] 郭琨, 杨树兴. 加速度峰值最小的落角约束导引律设计[J]. 战术导弹技术, 2017(6)：76-82.

GUO Kun, YANG Shu-xing. Minimax acceleration guidance law design with impact angle constraint[J]. Tactical Missile Technology, 2017(6):76-82. (in Chinese)

[11] Patterson M A, Rao A V. GPOPS-Ⅱ: a MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software, 2013, 39(3):1-41.

[12] Kim T H, Park B G, Tahk M J. Bias-shaping method for biased proportional navigation with terminal-angle constraint[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(6):1810-1816.

[13] Tekin R, Erer K S. Switched-gain guidance for impact angle control under physical constraints[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(2):205-216.

[14] Kim M, Grider K V. Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(6):852-859.

[15] Song T L, Shin S J. Time-optimal impact angle control for vertical plane engagements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2):738-742.

[16] 张春妍, 宋建梅, 侯博, 等. 带落角和时间约束的网络化导弹协同制导律[J]. 兵工学报, 2016, 37(3):431-438.

ZHANG Chun-yan, SONG Jian-mei, HOU Bo,et al. Cooperative guidance law with impact angle and impact time constraints for networked missiles[J]. Acta Armamentarii, 2016, 37(3):431-438.(in Chinese)

[17] 李强, 卢宝刚, 王晓辉, 等. 一种导弹终端侵彻多约束最优制导方法[J]. 兵工学报, 2016, 37(6):1131-1137.

LI Qiang, LU Bao-gang, WANG Xiao-hui,et al. A terminal multi-constraint optimal guidance law for missile[J]. Acta Armamentarii, 2016, 37(6):1131-1137.(in Chinese)

[18] Ryoo C K, Cho H, Tahk M J. Optimal guidance law with terminal impact angle constraint[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(4):724-732.

[19] Weiss M, Shima T. Optimal linear-quadratic missile guidance laws with penalty on command variability[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(2):226-237.

[20] Ben-Asher J Z, Grinfeld N. Minimal-jerk missile guidance law[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1520-1525.

[21] Lu P, Doman D, Schierman J. Adaptive terminal guidance for hypervelocity impact in specified direction[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2):269-278.

[22] Zhang Z, Li S, Luo S. Composite guidance laws based on sliding mode control with impact angle constraint and autopilot lag[J]. Transactions of the Institute of Measurement & Control, 2013, 35(6):764-776.

[23] Zhou D, Qu P, Sun S. A guidance law with terminal impact angle constraint accounting for missile autopilot[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(5):1-10.

[24] Kumar S R, Rao S, Ghose D. Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4):1114-1130.

[25] Lee C H, Kim T H, Tahk M J, et al. Polynomial guidance laws considering terminal impact angle and acceleration constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1):74-92.

[26] Lee Y I, Kim S H, Lee J I, et al. Analytic solutions of generalized impact-angle-control guidance law for first-order lag system[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1):96-112.

[27] Manchester I R, Savkin A V. Circular-navigation-guidance law for precision missile/target engagements[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2):314-320.

[28] 罗智林，刘藻珍，谢晓竹. 带进入角约束的组合导引律研究[J]. 兵工学报. 2010, 31(1): 32-36.

LUO Zhi-lin, LIU Zao-zhen, XIE Xiao-zhu. Research on integrated guidance law with the entry angle constraint[J]. Acta Armamentarii, 2010, 31(1): 32-36. (in Chinese)

[29] Ratnoo A, Ghose, D. Kill-band-based lateral impact guidance without line-of-sight rate information[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(6): 1740-1750.

[30] 胡锡精，黄雪梅. 具有落点和落角约束的圆轨迹制导律[J]. 宇航学报,2012, 33(5): 562-569.

HU Xi-jing, HUANG Xue-mei. Circular trajectory guidance law with terminal constraints of impact point and impact angle[J]. Journal of Astronautics, 2012, 33(5): 562-569. (in Chinese)

[31] 胡锡精，黄雪梅. 具有碰撞角约束的三维圆轨迹制导律[J]. 航空学报, 2012, 33(3): 508-519.

HU Xi-jing, HUANG Xue-mei. Three-dimensional circular guidance law with impact angle constraints[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 508-519. (in Chinese)

[32] Tsalik R, Shima T. Optimal guidance around circular trajectories for impact-angle interception[J]. Journal of Guidance Control, and Dynamics, 2016, 39(6):1-14.