手枪弹对带软防护的明胶靶标侵彻机理与实验研究

刘坤， 吴志林， 宁建国， 任会兰， 李忠新

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081；2.南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

近年来，防弹衣成为单兵防护装备的重要组成部分，在减少部队作战人员伤亡、提高单兵生存能力、增强作战效能方面发挥着重要作用。自美国杜邦公司于1939年发明并商业化生产尼龙纤维、1965年推出对位芳香族聚酰胺(Kevlar)纤维、荷兰DSM公司1970年推出强度更高的超高分子量聚乙烯(UHMWPE)纤维以来，高性能纺织纤维凭借其比强度和比模量较高、抗疲劳性能好、减震性能强、机械物理性能优良、具有良好的吸能性等特点，已成为软质防弹衣的重要原材料[1-5]。利用Kevlar或UHMWPE纤维制成的防弹衣，重量轻、质地柔软、适体性好、防护效果佳，内穿时具有较好的隐蔽性，能防住5 m以外手枪弹，且不会产生二次弹片，起到有效保护人体的作用，有效减少枪弹造成的贯穿性损伤。但仍有部分能量通过防弹衣变形传递给人体，造成器官损伤，这一现象称为“防弹衣后钝性损伤”(BABT)。

近年来，随着Kevlar和UHMWPE等纤维广泛应用于软质防弹衣中，其抗弹机理和钝性损伤的研究受到国内外学者的广泛关注。Flanagan等[6]进行了圆柱弹侵彻Kevlar纤维实验，认为纤维复合材料的破坏形式与弹体侵彻速度相关。刘元坤等[7]开展了三维机织复合材料侵彻实验研究，观测复合材料冲击破坏形态，并进行了数值仿真。顾冰芳等[8]利用不同形状弹体测试叠层织物弹道冲击性质，研究了UHMWPE纤维复合材料受冲击时的表观破坏形态、微观损伤机理及防弹性能影响因素。梅志远等[9]和王晓强等[10]进行了纤维复合材料侵彻实验研究，发现复合材料抗弹性能与其面密度相关。梁子青等[11]通过UHMWPE纤维侵彻实验，对其抗弹机理进行了分析。Smith等[12-13]研究了具有非线性应力应变特征的尼龙纱线横向冲击性能，并提出了单根无限长纱线横向冲击理论。Vinson等[14]基于静态圆锥壳理论，提出了弹体侵彻纤维时耗散能量的计算模型。Walker等[15]使用静态挠曲分析法，建立了织物与软质复合材料的冲击模型。顾伯洪[16]提出了基于纤维应变率效应的织物弹道冲击破坏分析模型，获得了不同应变率条件下不同层数平纹织物的弹道侵彻性能。Phoenix等[17]建立了弹体冲击下防弹织物破坏响应的分析模型，研究了钝头弹冲击二维薄膜的动态响应过程。Wen[18]提出了弹体侵彻层合板的经验模型，并分析了弹头所受侵彻阻力与层合板材料参数的关系。Naik等[19]研究了机织复合材料的弹道冲击性能，建立了基于应力波理论和能量守恒定律的分析模型。Leech等[20]、Laible[21]和Shim等[22]提出了基于变分原理的有限元和有限差分模型，由于缺少材料本构特性和破坏准则，模型计算结果与实测结果相反。Silva等[23]对弹体侵彻Kevlar纤维增强层合板进行了数值仿真，并获得了极限穿透速度。Duan等[24]通过ANSYS/LS-DYNA非线性有限元分析软件对球形破片侵彻单层小尺寸织物进行了数值模拟，并研究了交织点处摩擦、纱线与破片摩擦、边界条件等对吸收能量的影响。黄拱武[25]开展了弹体侵彻带UHMWPE纤维软防护明胶靶标的数值仿真，并进行了实验验证。罗少敏等[26-27]对弹体侵彻带软硬复合防护明胶靶标进行了数值模拟，分析了侵彻过程中典型现象及明胶靶标动态响应。夏清波等[28]利用ANSYS/LS-DYNA软件对立方体破片侵彻UHMWPE纤维层合板进行了数值模拟，并与文献中实验结果进行了对比，具有较好的一致性。王云聪等[29]开展了6.35 mm柱形弹侵彻Kevlar纤维层合板数值仿真研究，模拟了其抗侵彻过程，并与实验结果进行了对比，验证了模拟方法和模型参数的合理性。练军等[30]通过ANSYS/LS-DYNA软件对弹体侵彻三维编织复合材料进行了数值模拟，并与实验结果进行了对比，验证了采用细观结构的有限元模型进行弹道侵彻计算的合理性。陈晓等[31]借助ANSYS/LS-DYNA软件对破片侵彻复合材料防弹靶板进行了数值仿真，并分析了靶板抗弹机理和吸能方式。综上所述，由于弹体与目标之间相互作用的复杂性及防护材料破坏形式的多样性，国内外对防护抗弹机理和钝性损伤研究尚处于实验测试或数值仿真阶段，无法满足对致伤效应评估的要求。因此，开展非贯穿时弹头侵彻带软防护明胶靶标运动模型研究，有利于了解非穿透性伤害在人体组织中的力学响应，进而阐明钝击伤致伤机制，对提高防护性能及钝击伤治疗具有重要的意义。

基于前期就杀伤元侵彻明胶运动模型及明胶力学特性已开展大量工作[32-40]，本文以DC2-1型软质防弹衣为研究对象，针对弹道冲击软防护特性，分析手枪弹侵彻时软防护破坏形式，结合高应变率下UHMWPE纤维本构模型，并引入明胶弹性模型，建立手枪弹侵彻带软防护明胶靶标运动模型，力求为有防护目标杀伤机理和防护性能研究提供理论参考。

1 理论模型

DC2-1型软质防弹衣材料为UHMWPE无纬布(以UHMWPE纤维为基材，通过水溶性聚氨酯浸渍涂胶粘合)，其由46层薄纤维层叠合而成，每层纤维采用0/90正交复合层压而成(纤维直径为25 μm，软防护厚度为8 mm)。UHMWPE无纬布弹道冲击时，纤维应变率通常大于100 s-1，而现有手枪弹侵彻软防护模型均未考虑高应变率下的纤维特性，只有结合纤维在高应变率下性质，才能准确评估防护的防弹性能[8,11]。本节针对手枪弹侵彻软防护的特点，结合纤维高应变率下本构模型，并引入明胶弹性模型，对手枪弹侵彻带软防护明胶靶标运动模型展开研究。

1.1 纤维本构模型

软防护吸收冲击波能力取决于UHMWPE纤维的拉伸模量，拉伸模量越大，侵彻所引起扰动传播越快，吸收能量越大。因此，纤维本构模型是研究软防护抗弹性能和运动模型的基础与关键所在。

根据文献[41-43]可知，UHMWPE纤维本构模型可由Kelvin-Voigt体与弹簧K1串联的三单元体描述，如图1所示。

图1 软防护本构模型Fig.1 Soft body armor constitutive model

本构关系可表示为

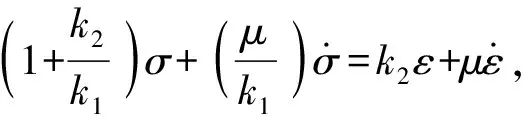
(1)

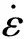
由(1)式积分，结合初始条件σ(0)=0可得

(2)

通过文献[41]可得，k1=160 GPa，k2=2.8 GPa，μ=3 MPa·s.

对(2)式求导可得

(3)

式中：E为纤维弹性模量。

1.2 运动模型

枪弹侵彻防护材料通常为小质量高速冲击，冲击过程中，枪弹与防护材料之间发生能量传递，主要包括以下3种情况[19]：

1) 贯穿防护材料，出靶时弹头具有一定速度，表明初始动能大于防护材料所吸收能量；

2) 不完全贯穿防护材料，弹头嵌入防护材料或跳弹，表明初始动能小于防护材料失效所吸收能量；

3) 贯穿防护材料，出靶时弹头剩余速度为0，表明弹头着靶速度为弹道极限，初始动能被防护材料完全吸收。

1.2.1 软防护破坏机理

手枪弹侵彻软防护时，防护材料将发生多种形式破坏，包括整体变形、局部压陷、纤维拔出与断裂等，可见弹头侵彻防护实质上为纤维阻碍弹头运动并吸收其能量的过程。根据手枪弹冲击作用下防护材料动力学性能和破坏失效现象，认为防护吸收能量的机理主要包括：防护材料背部隆起形成、主要纤维拉伸破坏、辅助纤维变形，如图2所示。

图2 弹头能量转化Fig.2 Energy conversion of pistol cartridge

图3 弹头侵彻防护时纤维中波的传播示意图Fig.3 Propagation of wave in fiber during penetrating

1) 防护材料背部隆起形成。与硬质防弹材料不同，软防护主要通过纤维变形吸收弹头动能达到防弹目的，防护材料背部隆起形成是纤维变形的一种体现。根据应力波理论，弹道冲击过程中，应力波沿纤维纵向/径向传播，波阵面形状类似双纽线/圆形，如图3所示。弹头以速度v侵彻软防护时，引起两个轴向应变波以速度cp向相反方向传播，波速越快，纤维与弹头相互作用越明显。弹头的冲击使纤维产生较大张力，自两侧向中央延伸，其后从撞击点产生横向波，沿纤维向两侧传播，使纤维产生横向运动，防护材料背面产生圆锥变形，形成倒V状隆起，P点为基脚，以速度u0向两侧传播。t时刻，F点以外纤维质点尚未受到冲击作用。

弹头侵彻防护时背部隆起形成如图4所示。图4中：d为弹头直径，ri为ti时刻隆起界面半径，zi为ti时刻弹头运动距离，ti为第i个时间间隔的时间。ri、zi随纤维中波的传递不断增大，直至所有纤维失效或弹头初始动能完全被防护材料吸收。

图4 防护材料背部隆起形成示意图Fig.4 Bulge of the back face of soft body armor impacted by pistol cartridge

2) 主要纤维拉伸破坏。弹头侵彻过程中，纵向波和横向波主要累及被撞击的纤维。弹头正下方纤维为主要纤维，产生阻碍弹头贯穿防护材料的力。高应变率情况下，纤维超过极限应变时发生拉伸失效，因此主要纤维拉伸将吸收弹头部分动能。纤维失效发生在应变集中处，应变通常沿纤维长度方向发生衰减，因此撞击边缘处应变最大。

3) 辅助纤维变形。由图4可知，隆起区域内除主要纤维外，其余纤维为辅助纤维。纵向波在纤维交结点将应力传递至辅助纤维，从而分散弹头撞击力。横向波引起的横向位移，使辅助纤维通过交结点受到纤维传来的应力作用。因此，辅助纤维由于变形也将吸收部分动能。辅助纤维吸收能量主要取决于其应变分布，A点应变和主要纤维相同，B点处应变已衰减至0，且A点至B点的应变变化为线性规律。

1.2.2 运动模型建立

结合1.1节纤维本构模型，建立手枪弹侵彻有软防护目标运动模型。弹头侵彻软防护时，总动能主要以4种形式耗散：防护背部隆起吸收能量EKE、主要纤维吸收能量ETF、辅助纤维吸收能量ED、明胶吸收能量EG.

建模前引入如下假设[19]：

1)弹头为刚体，忽略变形；

2)垂直侵彻防护材料；

3)冲击过程中，在某个时间间隔内弹头速度保持不变；

4)软防护材料各向同性；

5)单层纤维间相互独立；

6)纵波和横波在各层材料中传播速度保持不变。

侵彻过程中纵波传播相对未变形质点而言，应变波速度cp[19,44-45]为

(4)

式中：ρa为纤维密度。

对于横波传播，材料流动速度为w，即当纵向波通过后，图3中APF段纤维中质点开始向反方向收缩，速度可表示为

(5)

式中：εf为失效应变。

在横波前缘，质点水平运动停止，并以冲击速度v横向(向上)运动，假设横波向两侧移动速度相对于未变形质点为u，可表示为

(6)

式中：σf为失效应力。

当弹头撞击软防护时，其背面形成隆起。假设产生凹陷的横截面为圆形，凹陷底部半径变化速度为横波速度，可表示为

ct=u0=(1+εf)u-w.

(7)

联立(5)式、(6)式和(7)式可得

(8)

若将侵彻过程分成若干个时间间隔Δt，则第i个时间间隔横波和纵波传播规律分别为

(9)

式中：rti为横波运动距离；rpi为纵波运动距离。

侵彻过程中，纵波随应力波的反射和传播不断衰减。引入归一化应力σ′，并假设σ′为与撞击点距离相关的函数[19]，可表示为

(10)

式中：b为传输因子(常数)；a为纤维尺寸；x为距撞击点距离。

纵波传播的同时，其经过的纤维应变也发生变化，且弹头撞击点处应变最大。因此，归一化应力可表示为

(11)

单根纤维应变可表示为

(12)

结合(10)式、(11)式和(12)式可得

(13)

式中：εmax为单根纤维最大应变且出现在x=0处。

(13)式可表示为

(14)

未变形时单根纤维如图5所示，拉伸后纤维如图6所示。假设未变形前纤维长为Lc，拉伸后变为Ld，距撞击点x处取一微元dx1，拉伸后微元变为dx2，则应变为

(15)

图5 未变形时单根纤维Fig.5 Unstrained length of single fiber

图6 拉伸后单根纤维Fig.6 Stretched length of single fiber

联立(14)式和(15)式，可得

(16)

对(16)式两端积分得

(17)

由(16)式、(17)式可得

(18)

弹头侵彻前后防护纤维变化如图7所示。由图3和图7可知，当手枪弹横向侵彻软防护时，纤维变形前、后长度Lc、Ld分别为

Lc=rpi，

(19)

(20)

图7 弹头侵彻前后防护纤维变化Fig.7 Configuration of a fiber before and after transverse impact

结合(18)式、(19)式和(20)式，可得第i个时间间隔时，撞击点处主要纤维应变为

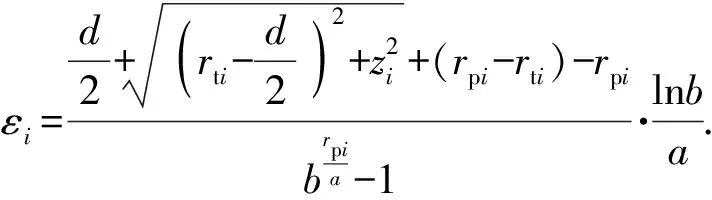
(21)

撞击开始阶段，能量以弹头动能形式存在，根据能量守恒定律，至第i个时间间隔，弹头损失总能量为防护材料和明胶所吸收能量，可表示为

Etoti=EKEi+ETFi+EDi+EGi，

(22)

式中：Etoti为至第i个时间间隔弹头损失的总能量；EKEi为至第i个时间间隔防护材料背部隆起的动能；ETFi为至第i个时间间隔主要纤维拉伸失效吸收能量；EDi为至第i个时间间隔辅助纤维变形吸收能量；EGi为至第i个时间间隔明胶吸收能量。

1)防护背部隆起吸收动能EKEi. 基于动能定理，假设防护背部形成隆起后隆起速度与弹头速度相同，(22)式可表示为

(23)

式中：m为弹头质量；v0为弹头初速；Mi为ti时刻形成隆起质量；vi为ti时刻弹头速度；Ei-1为至ti-1时刻内纤维和明胶所吸收能量，Ei-1可表示为

Ei-1=ED(i-1)+ETF(i-1)+EG(i-1).

(24)

由(23)式可得ti时刻弹头速度为

(25)

ti时刻防护背部形成隆起半径为ri，则防护背部形成隆起质量为

(26)

式中：h为防护厚度。

根据(26)式可知隆起动能EKEi为

(27)

由(25)式可得ti时刻弹头减加速度为

(28)

假设弹头侵彻软防护为匀减速运动，根据(28)式可知弹头运动距离为

(29)

(30)

2) 辅助纤维变形吸收能量EDi. 辅助纤维应变大小取决于距撞击点位置，靠近撞击处辅助纤维应变等于最外层主要纤维应变。因此，远离撞击点辅助纤维应变较小。图4中，点A、B处应变分别为

(31)

r=ri,εsy=0.

(32)

式中：r为辅助纤维任一点距撞击点的半径；ε0为距撞击点最远处主要纤维应变；εsy为辅助纤维应变。

假设从点A到点B的应变呈线性变化(见图4)，则有

εsyi=kεi，

(33)

式中：εi为ti时刻撞击点处主要纤维拉伸应变；εsyi为ti时刻辅助纤维应变。

假设k为r、ri、d的函数，则有

k=er+fri+gd，

(34)

式中：e、f、g为与ri、d相关的系数。

联立(31)式、(32)式、(34)式可得

(35)

(36)

由(34)式、(35)式和(36)式可得系数k为

(37)

则辅助纤维应变可表示为

(38)

辅助纤维中取半径为dr的微元，如图8所示。假设辅助纤维中应力为σsy，则微元中所存储变形能为

(39)

图8 辅助纤维变形示意图Fig.8 Modelling of energy absorbed due to deformation of secondary fiber

微元体积可表示为

dV=h{2πr-8rarcsin(d/2r)}dr，

(40)

则所有辅助纤维变形所吸收能量为

(41)

3)主要纤维拉伸失效吸收能量ETFi. 假设主要纤维中取长为dx、横截面积为S的微元，如图9所示，L为纤维长度。存储在微元dx中应变能为

(42)

式中：S为主要纤维横截面积；σ为主要纤维中应力。

图9 主要纤维示意图Fig.9 Primary fiber

若主要纤维中最大应变超过极限应变，则纤维发生拉伸失效。联立(2)式、(14)式、(42)式可得主要纤维失效吸收能量为

(43)

4)明胶吸收能量EGi. 明胶为与肌肉组织非常相似的黏弹性介质，假设弹头侵彻背后有明胶支撑的软防护时，可用弹簧模型模拟明胶靶标，如图10所示。弹头撞击防护时，防护后明胶产生弹性变形，并以波形式向周围传播。

图10 弹簧模型Fig.10 Schematic diagram of spring model

假设明胶仅受横向作用力，弹性波在明胶中传播距离为

s=cgt，

(44)

式中：s为弹性波在明胶中传播距离；cg为明胶中弹性波波速。

明胶所受横向作用力为

(45)

式中：Eg为明胶弹性模量。

明胶吸收能量可表示为

(46)

结合(22)式、(27)式、(41)式、(43)式、(46)式，手枪弹侵彻带软防护明胶靶标运动方程可描述为

(47)

综上所述，当手枪弹侵彻带软防护目标时，可根据防护背部隆起吸收动能、主要纤维拉伸失效吸收能量、辅助纤维变形吸收能量、明胶吸收能量，对防护的防弹性能和对人体组织钝击伤进行评估及预测。

2 理论分析与实验研究

为获得手枪弹侵彻带软防护目标的运动规律和致伤效果，分别选取9 mm全铜弹(均一硬质结构，弹头材料为黄铜H90)和92式5.8 mm手枪弹(钢芯铅柱被甲类)为杀伤元，其中9 mm全铜弹和92式5.8 mm手枪弹各2发，通过MATLAB软件对运动模型进行数值计算，获得2种弹头侵彻防护时速度、位移、防护背部隆起吸收动能、主要纤维拉伸失效吸收能量、辅助纤维变形吸收能量、明胶吸收能量随时间变化规律，并进行侵彻实验，弹头结构如图11所示，弹头参数如表1所示，软防护参数如表2所示。

图11 弹头结构图Fig.11 Structures of pistol cartridges

弹种d/mmv0/(m·s-1)m/gl/mm9mm全铜弹903240/26075517892式58mm手枪弹601300/340300214

注：l为弹头长度。

2.1 模型计算与理论分析

软防护虽能有效阻滞枪弹穿透，但无法阻挡所有枪弹。枪弹侵彻有软防护目标时，即使无法贯穿防护材料，中弹部位仍受到钝击载荷作用，目标也会产生损伤。本节主要选取9 mm全铜弹和92式5.8 mm手枪弹为杀伤元，对侵彻有软防护目标时的运动规律和作用效果进行理论分析。

表2 软防护参数

注：εf为断裂伸长率，σf为失效应力。

2.1.1 9 mm全铜弹理论计算结果分析

选取9 mm全铜弹2发，通过1.2节中(24)式、(25)式、(27)式、(29)式、(41)式、(43)式、(46)式对侵彻有软防护目标的运动规律进行分析。第1发入靶速度为260 m/s，位移、速度随时间变化关系曲线分别如图12和图13所示。由图12和图13可知：弹头侵彻时间为34.7 μs时，位移为0.008 0 m；运动时间为38.0 μs时，位移达到最大值0.008 4 m. 可见，入靶速度为260 m/s时，弹头能够穿透防护。

图12 9 mm全铜弹第1发位移与时间关系曲线Fig.12 Displacement vs. time for the first 9 mm×17.8 mm copper pistol cartridge

图13 9 mm全铜弹第1发速度与时间关系曲线Fig.13 Velocity vs. time for the first 9 mm × 17.8 mm copper pistol cartridge

辅助纤维吸收能量、隆起动能随时间变化曲线分别如图14(a)和图14(b)所示。由图14(a)可知，辅助纤维变形吸收能量随侵彻时间增加而增大，弹头停止运动时，辅助纤维变形所吸收能量达160.0 J，占总能量63%. 由图14(b)可知，侵彻初期隆起动能随侵彻时间增加而增大，在侵彻时间为28.0 μs时，隆起动能达到最大值9.0 J，后期隆起动能随速度衰减而减小，直至为0. 图14(c)和图14(d)分别为主要纤维、明胶吸收能量随时间变化曲线。由图14(c)可知，主要纤维吸收能量随侵彻时间增加而增大，且在侵彻初期增长较快，至弹头停止运动达到最大值23.0 J. 由图14(d)可知，明胶吸收能量随运动时间增加而增大，弹头停止运动时，明胶吸收能量达到最大值63.0 J，占总能量25%.

图14 9 mm全铜弹第1发侵彻有软防护目标能量随时间变化理论曲线Fig.14 Absorbed energies vs. time for the first 9 mm×17.8 mm copper pistol cartridge

第2发入靶速度为240 m/s，位移、速度随时间变化关系曲线分别如图15和图16所示。由图15和图16可知，弹头运动时间为37.0 μs，位移最大值为0.007 2 m. 可见，入靶速度为240 m/s时，弹头未穿透防护。

图15 9 mm全铜弹第2发位移随时间变化理论曲线Fig.15 Displacement vs. time for the second 9 mm×17.8 mm copper pistol cartridge

图16 9 mm全铜弹第2发速度随时间变化理论曲线Fig.16 Velocity vs. time for the second 9 mm×17.8 mm copper pistol cartridge

辅助纤维吸收能量、隆起动能随时间变化曲线分别如图17(a)和图17(b)所示。由图17(a)可知，弹头停止运动时，辅助纤维变形吸收能量为140.0 J，占总能量64%. 由图17(b)可知，侵彻时间为27.0 μs时，隆起动能达到最大值7.5 J. 图17(c)和图17(d)分别为主要纤维、明胶吸收能量随时间变化曲线，弹头停止运动时，主要纤维、明胶吸收能量分别达到最大值22.0 J、48.0 J，明胶吸收能量占总能量22%.

综上可知：入靶速度为260 m/s时，弹头穿透防护，穿透防护时间为34.7 μs，在38.0 μs时停止运动，明胶吸收能量最大为63.0 J；入靶速度为240 m/s时，弹头未穿透防护，侵彻时间为37.0 μs，明胶吸收能量最大为48.0 J. 经计算可得，9 mm全铜弹极限穿透速度为256.0 m/s.

2.1.2 92式5.8 mm手枪弹理论计算结果分析

选取2发92式5.8 mm手枪弹，第1发入靶速度为300 m/s，位移、速度随时间变化关系曲线分别如图18和图19所示。由图18和图19可知，弹头侵彻防护时间为27.0 μs时，位移达到最大值0.006 8 m. 可见，入靶速度为300 m/s时，弹头未穿透防护。

辅助纤维吸收能量、隆起动能随时间变化曲线分别如图20(a)和图20(b)所示。由图20(a)可知，弹头停止运动时，辅助纤维变形吸收能量为78.0 J，占总能量58%. 由图20(b)可知，侵彻时间为20.0 μs时，隆起动能达到最大值7.0 J. 图20(c)和图20(d)分别为主要纤维、明胶吸收能量随时间变化曲线，主要纤维、明胶吸收能量分别达到最大值18.0 J、32.0 J，明胶吸收能量占总能量24%.

第2发入靶速度为340 m/s，位移、速度随时间变化关系曲线分别如图21和图22所示。由图21和图22可知：弹头侵彻时间为27.0 μs时，位移达到0.008 0 m；弹头停止运动时，侵彻位移达到最大值0.008 1 m. 可见，入靶速度为340 m/s时，弹头能够穿透防护。

辅助纤维吸收能量、隆起动能随时间变化曲线分别如图23(a)和图23(b)所示。由图23(a)可知，弹头位移为0.008 0 m时，辅助纤维变形吸收能量为70.0 J；停止运动时，辅助纤维变形吸收能量达99.0 J，占总能量57%. 由图23(b)可知，侵彻时间为21.0 μs时，隆起动能达到最大值9.0 J. 图23(c)和图23(d)分别为主要纤维、明胶吸收能量随时间变化曲线。由图23(c)可知，弹头停止运动时，主要纤维吸收能量达到最大值19.0 J. 由图23(d)可知：侵彻位移为0.008 0 m时，明胶吸收能量为43.0 J；停止运动时，明胶吸收能量达到最大值46.0 J，占总能量27%.

图17 9 mm全铜弹第2发能量随时间变化理论曲线Fig.17 Absorbed energy vs. time for the second 9 mm×17.8 mm copper pistol cartridge

图18 5.8 mm手枪弹第1发位移与时间变化Fig.18 Displacement vs. time for the first 5.8 mm×21.4 mm pistol cartridge

图19 5.8 mm手枪弹第1发速度与时间变化Fig.19 Velocity vs. time for the first 5.8 mm×21.4 mm pistol cartridge

图20 5.8 mm手枪弹第1发侵彻有软防护目标能量随时间变化理论曲线Fig.20 Absorbed energy vs. time for the first 5.8 mm×21.4 mm pistol cartridge

图21 5.8 mm手枪弹第2发位移随时间变化理论曲线Fig.21 Displacement vs. time for the second 5.8 mm×21.4 mm pistol cartridge

图22 5.8 mm手枪弹第2发速度随时间变化理论曲线Fig.22 Velocity vs. time for the second 5.8 mm×21.4 mm pistol cartridge

综上可知：当入靶速度为300 m/s时，弹头未穿透防护，运动时间为27.0 μs，明胶吸收能量最大为32.0 J；入靶速度为340 m/s时，弹头穿透防护，明胶吸收能量最大为46.0 J. 经计算可得，92式5.8 mm手枪弹极限穿透速度为337.0 m/s.

2.2 实验研究

为验证手枪弹侵彻带软防护目标理论模型，进行侵彻实验，实验流程如图24所示。实验分别采用9 mm、5.8 mm弹道枪作为发射平台，共射击20发，分别选取9 mm全铜弹、92式5.8 mm制式手枪弹各10发，发射装置如图25所示。采用4℃温度、配比为10%明胶作为靶标(尺寸为300 mm×300 mm×300 mm)，并在靶标前通过专用夹具固定软质防弹衣(尺寸为300 mm×300 mm)，如图26所示。

实验原理与场景分别如图27和图28所示，光电靶置于距离靶标2.0 m处测量入靶速度，靶标沿弹道方向置于综合靶架上，光幕和气体灯置于距离靶标侧1.0 m处(气体灯置于光幕后)，高速摄像机(Phantom V12.1，分辨率512×256，用于拍摄弹头侵彻过程)置于距离靶标另一侧1.5 m处，确保高速摄像机镜头轴线与弹道在同一平面内，且与弹道方向垂直。由于实验测量难度较大，本文实验无法获取主要纤维、辅助纤维、明胶变形及隆起所吸收能量，仅测得2种手枪弹的极限穿透速度。

2.2.1 9 mm全铜弹实验结果

选取10发9 mm全铜弹，获得侵彻有软防护靶标临界穿透速度。实验中通过调节装药量，使弹头着靶速度在200～300 m/s范围内。实验结果如表3所示。

可见，弹头穿透有软防护靶标极限穿透速度为278.4 m/s，由2.1节可知，模型所得极限穿透速度为256.0 m/s，相对误差为8.0%；未穿透防护时弹头发生轻微墩粗变形，变形范围约为0.4～2.3 mm.

图24 实验流程Fig.24 Experimental process

图25 发射装置Fig.25 Launcher

图26 实验靶标Fig.26 Target

图27 实验原理Fig.27 Schematic diagram of experimental system

图28 实验场景Fig.28 Experimental setup for image capturing

实验号v0/(m·s-1)Npl/mmzf/mmrf/mm12201215667622258251657167327646176807042673617472685220181556864627346177807072754617680708271461767969929746176837410294441738273

注：Np为穿透层数，zf为最终侵彻深度，rf为最终隆起半径。

9 mm全铜弹剩余速度vr与初速关系曲线如图29所示。从图29中可看出，初速分别为276 m/s、294 m/s、300 m/s时，剩余速度理论值分别为90.9 m/s、95.3 m/s、96.2 m/s，实验值分别为94.3 m/s、97.4 m/s、101.1 m/s，相对误差分别为3.6%、2.2%、4.8%.

图29 9 mm全铜弹剩余速度与初速关系Fig.29 Relationship between residual velocity and muzzle velocity for 9 mm×17.8 mm copper pistol cartridge

9 mm全铜弹剩余能量对比曲线如图30所示。从图30中可看出，初速分别为276 m/s、294 m/s、300 m/s时，剩余能量理论值分别为31.2 J、34.3 J、34.9 J，实验值分别为33.6 J、35.8 J、38.6 J，相对误差分别为7.1%、4.2%、9.6%.

图30 9 mm全铜弹剩余能量对比Fig.30 Comparision of residual kinetic energies of 9 mm×17.8 mm copper pistol cartridge

弹头未穿透有软防护目标侵彻过程如图31所示，穿透有软防护目标侵彻过程如图32所示，图33和图34分别为软防护和弹头侵彻前后对比。可见，弹头侵彻防护后，撞击区域纤维及其周边辅助纤维发生变形，防护背部产生隆起，同时明胶产生鼓包共同吸收弹头能量，较好验证了1.2.1节中分析结果。

图31 9 mm全铜弹未穿透有软防护目标时侵彻过程Fig.31 Penetrating process of 9 mm pistol cartridge without penetrating into soft armor

图32 9 mm全铜弹穿透有软防护目标时侵彻过程Fig.32 Process of 9 mm pistol cartridge penetrating into soft armor

图33 软防护侵彻前后对比Fig.33 Comparison of soft armors before and after penetration

图34 9 mm全铜弹侵彻前后对比Fig.34 Comparison of 9 mm pistol cartridges before and after penetration

2.2.2 92式5.8 mm手枪弹实验结果

选取10发92式5.8 mm手枪弹，通过减装药调整弹头初速，获得侵彻有软防护靶标临界穿透速度。实验结果如表4所示。

由表4可见，92式5.8 mm手枪弹极限穿透速度为346 m/s，由2.1.2节中可知，模型所得极限穿透速度为337.0 m/s，相对误差为2.6%.

表4 92式5.8 mm手枪弹侵彻有软防护目标实验结果

弹头穿透有软防护目标侵彻过程如图35所示。图36为穿透后的软防护，图37为回收的弹头。由图35可知，弹头穿透软防护后背部隆起较小。将回收的弹头进行测量，弹头质量和长度未发生变化。结果表明，92式5.8 mm制式手枪弹(制式弹初速为480 m/s)均能穿透软质防弹衣，且弹头未发生变形。

图35 92式5.8 mm手枪弹穿透有软防护目标时侵彻过程Fig.35 Process of 5.8 mm pistol cartridge penetrating into soft armor

图36 穿透后的软防护Fig.36 Soft armor penetrated by 5.8 mm pistol cartridge

图37 回收的92式5.8 mm手枪弹弹头Fig.37 Recovered 5.8 mm pistol cartridge

3 结论

本文针对手枪弹侵彻软防护特点，结合纤维高应变率下本构模型，分析手枪弹侵彻软防护时破坏形式，并引入明胶弹性模型，建立了非贯穿时手枪弹侵彻带软防护明胶靶标运动模型。选取9 mm全铜弹(均一硬质结构)和92式5.8 mm手枪弹(钢芯铅柱被甲类)为杀伤元，对模型进行了数值计算和实验验证，得出以下结论：

1)通过分析手枪弹侵彻软防护的破坏形式可知，防护吸收能量方式主要有防护材料背部隆起形成、主要纤维拉伸破坏、辅助纤维变形。

2)均一硬质结构和钢芯铅柱被甲类杀伤元在一定速度下均能穿透软防护，侵彻过程中辅助纤维变形和明胶吸收能量占总动能比例较大，该模型可为有防护目标杀伤机理和防护性能研究提供理论参考。

)

[1] Prevosek D C, Chin H B. Ballistic armor from extended chain polyethylene fibers[C]∥33rd International SAMPE Symposium and Exhibition. CA, US: NASA, 1988.

[2] Prevosek D C, Chin H B. Properties of spectra fibers and compo-sites at ballistic rates of deformation[C]∥21st International SAMPE Technical Conference. AH, US: NASA, 1989.

[3] Bhatnagar A. Comparison of ballistic performance of composites[C]∥34th International SAMPE Symposium and Exhibition. CA, US: NASA, 1989.

[4] 胡晓兰, 王东, 石毓锬, 等. 用于人体防护装甲的纤维复合材料的研究[J]. 纤维复合材料, 2000, 40(2): 40-44.

HU Xiao-lan, WANG Dong, SHI Yu-tan, et al. Study on fiber composite for human body protective armor[J]. Fiber Composites, 2000, 40(2): 40-44. (in Chinese)

[5] 顾伯洪, 孙宝忠. 纺织结构复合材料冲击动力学[M]. 北京:科学出版社, 2012.

GU Bo-hong, SUN Bao-zhong.Textile structure of composite impact dynamics[M]. Beijing: Science Press, 2012. (in Chinese)

[6] Flanagan M P, Zikry M A, Wall J W, et al. An experimental investigation of high velocity impact and penetration failure modes in textile composites[J]. Journal of Composite Materials, 1999, 33(12): 1080-1103.

[7] 刘元坤. 三维正交机织复合材料弹道冲击破坏:实验研究和有限元计算[D]. 上海: 东华大学, 2008.

LIU Yuan-kun. Ballistic impact damage of 3D orthogonal woven composites: experimental study and finite element analysis[D]. Shanghai:Donghua University, 2008. (in Chinese)

[8] 顾冰芳, 龚烈航, 徐国跃. UHMWPE纤维复合材料防弹机理和性能[J]. 纤维复合材料, 2006, 23(1): 20-23.

GU Bing-fang, GONG Lie-hang, XU Guo-yue. Ballistic resistance mechanism and performance of UHMWPE composites[J]. Fiber Composites, 2006, 23(1): 20-23.(in Chinese)

[9] 梅志远, 朱锡, 任春雨, 等. 弹道冲击下层合板破坏模式及抗弹性能实验研究[J]. 海军工程大学学报, 2005, 17(1): 11-15.

MEI Zhi-yuan, ZHU Xi, REN Chun-yu, et al. Research of deformation model and resistance characteristic for laminates under ballistic impact[J]. Journal of Naval University of Engineering, 2005, 17(1): 11-15. (in Chinese)

[10] 王晓强, 朱锡, 梅志远, 等. 超高分子量聚乙烯纤维增强层合厚板抗弹性能实验研究[J]. 爆炸与冲击, 2009, 29(1): 29-34.

WANG Xiao-qiang, ZHU Xi, MEI Zhi-yuan, et al.Ballistic performances of ultra-high molecular weight polyethylene fiber-reinforced thick laminated plates[J]. Explosion and Shock Waves, 2009, 29(1): 29-34. (in Chinese)

[11] 梁子青, 周庆, 邱冠雄, 等. UHMWPE纤维/LDPE复合材料防弹性能及机理研究[J]. 纤维复合材料, 2002, 19(4): 6-9.

LIANG Zi-qing, ZHOU Qing, QIU Guan-xiong, et al. A study on ballistic performance and mechanism of UHMWPE fiber/LDPE composites[J]. Fiber Composites, 2002, 19(4): 6-9. (in Chinese)

[12] Smith J C, McCrackin F L, Schiefer H F. Stress-strain relationships in yarns subjected to rapid impact loading Part Ⅴ: wave propagation in long textile yarns impacted transversely[J]. Textile Research Journal, 1958, 28(4): 288-302.

[13] Smith J C, Blanford J H, Towne K H. Stress-strain relationships in yarns subjected to rapid impact loading Part Ⅷ: shock waves, limiting breaking velocities, and critical velocities[J]. Textile Research Journal, 1962, 32(1): 67-76.

[14] Vison J R, Walker J M. Ballistic impact of thin-walled composite structures[J]. AIAA Journal, 2015, 35(5): 875-878.

[15] Walker J D. Ballistic limits of fabrics with resin[C]∥19th International Symposium of Ballistic. Interlaken, Switzerland:IBS, 2001: 1409-1414.

[16] 顾伯洪. 织物弹道贯穿性能分析计算[J]. 复合材料学报, 2002, 19(6): 92-96.

GU Bo-hong. An analytical modelling of woven fabric under ballistic perforation[J]. Acta Materiae Compositae Sinica, 2002, 19(6): 92-96. (in Chinese)

[17] Phoenix S L, Porwal P K. A new membrane model for the ballistic impact response andv50performance of multi-ply fibrous systems[J]. International Journal of Solids and Structures, 2003, 40: 6723-6765.

[18] Wen H M. Penetration and perforation of thick FRP laminates[J]. Composites Science & Technology, 2001, 61(8): 1163-1172.

[19] Nail N K, Shrirao P, Reddy B C K. Ballistic impact behavior of woven fabric composites: formulation[J]. International Journal of Impact Engineering, 2006, 32(9):1521-1552.

[20] Leech C, Hearle J W S, Mansell J. A variational model for the arrest of projectiles by woven cloth and nets[J]. Journal of the Textile Institute, 1979, 70(11):469-478.

[21] Laible R C. Ballistic materials and penetration mechanics[M]. Amsterdam, Holland: Elsevier Scientific Publishing Company, 1980.

[22] Shim V P W, Tan V B C, Tay T E. Modeling deformation and damage characteristics of woven fabrics under small projectile impact[J]. International Journal of Impact Engineering, 1995, 16(4): 585-605.

[23] Silva M A G, Cismasiu C, Chiorean C G. Numerical simulation of ballistic impact on composite laminates[J]. International Journal of Impact Engineering, 2005, 31: 289-306.

[24] Duan Y, Keefe M, Bogetti T A, et al. Modeling friction effects on the ballistic impact behavior of s single-ply high-strength fabric[J]. International Journal of Impact Engineering, 2005, 31(8): 996-1012.

[25] 黄拱武. 弹体撞击带纤维软防护明胶靶标的数值仿真研究[D]. 南京: 南京理工大学, 2013.

HUANG Gong-wu.Numerical simulation of bullets penetrating into gelatin target with soft armor[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)

[26] 罗少敏. 小质量物体高速撞击陶瓷复合靶板毁伤效应研究[D]. 南京: 南京理工大学, 2013.

LUO Shao-min. Damage effects of small mass objects impacting on ceramic composite targets at high velocity[D]. Nanjing: Nanjing University of Science and Technology, 2013. (in Chinese)

[27] 罗少敏, 徐诚, 陈爱军, 等. 步枪弹侵彻带软硬复合防护明胶靶标的数值模拟[J]. 兵工学报, 2014, 35(8): 1172-1178.

LUO Shao-min, XU Cheng, CHEN Ai-jun, et al. Numerical simulation of bullets penetrating into gelatin target with hard/soft composite armor[J]. Acta Armamentarii, 2014, 35(8): 1172-1178. (in Chinese)

[28] 夏清波, 晏麓晖, 冯兴民. UHMWPE纤维层合板抗弹侵彻数值模拟[J]. 四川兵工学报, 2011, 32(2): 119-121.

XIA Qing-bo, YAN Lu-hui, FENG Xing-min. Numerical simulation of penetration into UHMWPE laminates[J]. Journal of Sichuan Ordnance, 2011, 32(2): 119-121. (in Chinese)

[29] 王云聪, 何煌, 曾首义. Kevlar纤维层合板抗弹性能的数值模拟[J]. 四川兵工学报, 2011, 32(3): 17-20.

WANG Yun-cong, HE Huang, ZENG Shou-yi.Numerical simulation of anti-resilience for Kevlar fiber laminate[J]. Journal of Sichuan Ordnance, 2011, 32(3): 17-20. (in Chinese)

[30] 练军, 顾伯洪. 三维编织复合材料弹道冲击细观结构模型的有限元计算[J]. 弹道学报, 2006, 18(3): 79-83.

LIAN Jun, GU Bo-hong. Microstructure model for finite element calculation of 4 steps 3D rectangular braided composites under ballistic impact[J]. Journal of Ballistic, 2006, 18(3): 79-83. (in Chinese)

[31] 陈晓, 周宏, 王西亭. 叠层靶板的弹道侵彻数值仿真[J]. 兵工学报, 2004, 25(3): 340-344.

CHEN Xiao, ZHOU Hong, WANG Xi-ting. Numerical simulation of ballistic penetration of laminated composite panels[J].Acta Armamentarii, 2004, 25(3): 340-344. (in Chinese)

[32] Liu K, Ning J G, Wu Z L,et al. A comparative investigation on motion model of rifle bullet penetration into gelatin[J]. International Journal of Impact Engineering, 2017, 103: 169-179.

[33] Liu K, Wu Z L, Ren H L, et al. Strain rate sensitive compressive response of gelatine: experimental and constitutive analysis[J]. Polymer Testing, 2017, 64: 254-266.

[34] 刘坤, 吴志林, 徐万和, 等. 弹头侵彻明胶的运动模型[J]. 爆炸与冲击, 2012, 32(6): 616-622.

LIU Kun, WU Zhi-lin, XU Wan-he, et al. A motion model for bullet penetrating gelatin[J]. Explosion and Shock Waves, 2012, 32(6): 616-622. (in Chinese)

[35] 刘坤, 吴志林, 徐万和, 等. 球形破片侵彻明胶的修正力学模型[J]. 南京理工大学学报, 2012, 36(5): 755-761.

LIU Kun, WU Zhi-lin, XU Wan-he, et al.Correction mechanical model of spherical fragments penetrating gelatin[J]. Journal of Nanjing University of Science and Technology, 2012, 36(5): 755-761. (in Chinese)

[36] 刘坤, 吴志林, 徐万和, 等. 弹头侵彻明胶运动模型参数研究[J]. 高压物理学报, 2013, 27(5): 677-684.

LIU Kun, WU Zhi-lin, XU Wan-he, et al. Research on model parameters of bullet penetrating gelatin[J]. Chinese Journal of High Pressure Physics, 2013, 27(5): 677-684. (in Chinese)

[37] 刘坤, 吴志林, 徐万和, 等. 3种小口径步枪弹的致伤效应[J]. 爆炸与冲击, 2014, 34(5): 608-614.

LIU Kun, WU Zhi-lin, XU Wan-he, et al. Wounding effects of three kinds of small caliber rifle cartridges[J]. Explosion and Shock Waves, 2014, 34(5): 608-614. (in Chinese)

[38] 莫根林, 吴志林, 刘坤. 球形破片侵彻明胶的瞬时空腔模型[J]. 兵工学报, 2013, 34(10): 1324-1329.

MO Gen-lin, WU Zhi-lin, LIU Kun. Temporary cavity model of spherical fragments penetrating ballistic gelatin[J]. Acta Armamentarii, 2013, 34(10): 1324-1329. (in Chinese)

[39] 莫根林, 吴志林, 冯杰, 等. 步枪弹侵彻明胶的表面受力模型[J]. 兵工学报, 2014, 35(2): 164-170.

MO Gen-lin, WU Zhi-lin, FENG Jie, et al. Surface pressure model of rifle bullets penetrating into ballistic gelatin[J]. Acta Armamentarii, 2014, 35(2): 164-170. (in Chinese)

[40] 刘坤, 宁建国, 吴志林, 等. 球形破片侵彻明胶运动模型对比研究[J]. 中国科学: 技术科学, 2017, 47: 1081-1092.

LIU Kun, NING Jian-guo, WU Zhi-lin,et al. A comparative investigation on motion model of spherical fragments penetration into gelatin[J]. Scientia Sinica Technologica, 2017, 47: 1081-1092. (in Chinese)

[41] Wambua P, Vangrimde B, Lomov S, et al. The response of natural fiber composites to ballistic impact by fragment simulating projectiles[J]. Composite Structures, 2007, 77(2): 232-240.

[42] Lim C T, Shim V P, Ng Y H. Finite-element modeling of the ballistic impact of fabric armor[J]. International Journal of Impact Engineering, 2003, 28(1): 13-31.

[43] Shim V P, Lim C T, Foo K J. Dynamic mechanical properties of fabric armor[J]. International Journal of Impact Engineering, 2001, 25(1): 1-15.

[44] 熊杰, 顾伯洪, 王善元. 防弹层压复合材料防弹效果的理论分析[J]. 纺织学报, 2003, 24(5): 47-48.

XIONG Jie, GU Bo-hong, WANG Shan-yuan.The theoretical analysis of the effect of bulletproof laminated composites[J]. Journal of Textile Research, 2003, 24(5): 47-48. (in Chinese)

[45] Velmurugan R, Sikarwar R S, Gupta N K. Analytical modeling for ballistic perforation of angle-ply and hybrid composite laminates[C]∥IMPLAST 2010 Conference. RI, US: SEM, 2010.