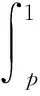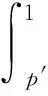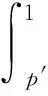剩余分位Extropy序的进一步研究
贾 锴, 俞锦涛
(陆军炮兵防空兵学院 基础部数学教研室,安徽 合肥 230031)
1 预备知识
设X为一非负连续型随机变量,其概率密度函数为f,为了度量X中所包含的不确定性,文献[1]定义X的香农熵(Entropy)如下:
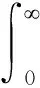
最近,文献[2]定义了一个新的不确定性的度量,并称之为Extropy。对于非负连续型随机变量X,定义其Extropy如下:
J(X)和H(X)互为补对偶,更多关于Extropy与香农熵的相关性质可参阅文献[2,3]。
若X表示一个新元件的寿命,该元件t时刻仍正常工作,它能继续工作的寿命称为其在t时刻的剩余寿命,记为Xt,由定义知Xt=(X-t|X>t)。因元件已经工作到t时刻,再考察X中所包含的不确定性已不适合。文献[4]指出不确定性应该是时间t的函数,并建议改为度量Xt中包含的不确定性。基于这个思想,文献[5]将X在t时刻的剩余Extropy定义如下:
(1)

非负连续型随机变量X的概率分布还可以用分位函数表示,分位函数的定义为:
F-1(p)=inf {x|F(x)≥p},p∈(0,1)。
分布函数与分位函数在某种意义下是等价的,文献[6,7]分别介绍了基于分位函数的概率模型及其在可靠性理论中的应用。文献[8]首次将分位函数引入不确定性的度量,类比其过程,令式(1)中的t=F-1(p),得到X的剩余分位Extropy如下:
其中第二个等号利用变量代换u=F(x)得到。QJp(X)从Extropy的角度度量了X在已经工作了100p%的寿命后所剩余的不确定性,是一种基于分位函数的不确定性的度量。为了比较两个随机变量所包含的不确定性的大小,借助剩余分位Extropy提出一个新的随机序,称之为剩余分位Extropy(LQEx)序。
定义1.1称X依LQEx序小于Y,如果QJp(X)QJp(Y)对于所有的p∈(0,1)都成立,记为XLQExY。
下面的引理1.2给出LQEx序的一个等价判别,其证明可由剩余分位Extropy的定义直接得到,故省略。该引理在本文的证明过程中将被反复使用。
引理1.2设随机变量X、Y的概率密度函数分别为f、g,分位函数分别为F-1、G-1,则XLQExY,当且仅当对于所有的p∈(0,1),
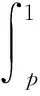
本文将集中研究LQEx序的性质,具体安排如下:第二节分析了LQEx序与其他随机序的关系,并给出由凸变换序得到LQEx序的条件。第三节讨论非线性变换下的LQEx序,建立了随机变量的非线性变换依LQEx序大于或小于其本身的充分条件,并讨论了LQEx序经非线性变换后封闭的条件。第四节研究了试验总时间变量与原随机变量之间的LQEx序,以及LQEx序在试验总时间变换中的封闭性。第五节分析由同分布但可能相依的元件构成的一般单调关联系统的寿命,借助控制函数研究了LQEx序在一般的单调关联系统中的封闭性。
2 LQEx序与其他随机序的关系
本节研究LQEx序与其他随机序之间的关系,首先介绍一些常用随机序的定义以及其基本性质,有关这些随机序的更多内容还可参考文献[9]。

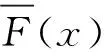
(b)称X依色散序小于Y,若f(F-1(p))≥g(G-1(p))对所有的p∈(0,1)都成立,记为XdispY;
(c)称X依凸变换序小于Y,若G-1F(x)在(0,)上凸,记为XcY。
结合色散序的定义以及引理1.2分析可知XdispY⟹XLQExY。下面的定理2.2进一步研究凸变换序和LQEx序的关系。
定理2.2若XcY,则XLQExY当且仅当J(X)J(Y)。

h′(p) =g(G-1(p))-f(F-1(p))
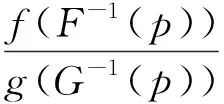
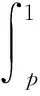

例2.4令X的分布函数F(x)=1-exp (-2x2),x≥0,Y的分布函数G(x)=1-e-x,x≥0,则G-1F(x)=2x2为凸,即XcY。另外
于是由定理2.2可知XLQExY。
3 非线性变换下的LQEx序

定理3.1设X为一非负连续型随机变量,φ是一个严格递增的函数,且满足φ(0)=0,
(a)若φ′(x)≥1对所有的x>0都成立,则XLQExφ(X);
(b)若0<φ′(x)1对所有的x>0都成立,则φ(X)LQExX。
证(a)对于所有的p∈(0,1)都有
≥0
其中不等式由条件φ′(x)≥1得。则由引理1.2可得XLQExφ(X)。
(b)的证明类似。
下面的推论3.2和例3.3分别给出定理3.1的一个简单推广和重要应用。
推论3.2设X为一非负连续型随机变量,
(a)若θ≥1,则XLQExθX;
(b)若0<θ1,则θXLQExX。
例3.3令X服从参数为λ的指数分布,φ(x)=log (1+λγx/β)/γ,其中γ>0,β≥λ>0,则φ(X)服从参数为(β,γ)的Gompertz-Makeham分布,其分布函数Fφ(x)=1-exp [-β(eγx-1)/γ],x≥0。因为φ′(x)=λ/(β+λγx)1,所以由定理2.1可知φ(X)LQExX。即有QJp(φ(X))QJp(X)=-λ/4。
接下来我们考虑,如果随机变量X和Y存在LQEx序的关系,那么这种关系在经过φ变换后能否保留。首先介绍如下引理:
引理3.4[10]设μ(x)是(a,b)上的测度,其中-a 定理3.5令XLQExY,若YstX且φ(x)是一个严格递增的凹函数满足φ(0)=0,则有φ(X)LQExφ(Y)。 证由引理1.2可知,XLQExY时[f(F-1(u))-g(G-1(u))]du≥0对于所有的p∈(0,1)都成立。同样根据引理1.2,只需证≥0对于所有的p∈(0,1)都成立即可,其中分别表示φ(Y)的密度函数和分位函数。注意到YstX意味着G-1(x)F-1(x),且φ(x)是凹函数,所以 另一方面,φ(x)是一个严格递增的凹函数,故1/φ′(F-1(u))是非负且单调递增的,则由引理3.4可知上式右端恒大于0,结论证毕。 Barlow等人于1972年首次提出试验总时间(total time on test)变量的概念,并将其运用于凸变换序的检验[11]。之后,这种变换的性质被广泛研究与运用,其成果可参阅文献[12]。本节将首先介绍试验总时间变量的定义,然后研究试验总时间变量在LQEx序中的应用。 (2) 定义4.2称X依试验总时间序小于Y,如果 对所有的p∈(0,1)都成立,记为XtttY。 结合定义4.1和4.2知,XtttY的充要条件是XtttstYttt,且若XstY,则XtttY。 性质4.3XtttLQExX。 证对式两边求导得 其中fttt表示Xttt的密度函数。整理上式得 (3) 于是由引理3.4得XtttLQExX。 例4.4设X和Y分别服从参数为1指数分布,由定义4.1得其试验总时间变量Xttt服从(0,1)上的均匀分布再由定理4.3可得 定理4.5若XLQExY,则XtttLQExYttt。 证由XLQExY可知[f(F-1(u))-g(G-1(u))]du≥0对于所有p∈(0,1)都成立,注意到式(3)可得 即XtttLQExYttt。 单调关联系统是可靠性理论中满足单调性和关联性两个最基本公理的系统。单调性即系统中元件可靠性的降低不会使系统可靠性提高,关联性即系统中不存在无用元件,每个元件都与系统有关。设系统中各元件寿命为一随机向量X=(X1,…,Xn),其中Xi表示第i个元件的寿命。系统寿命T是元件寿命的函数,即T=φ(X1,…,Xn),φ是系统结构函数。元件之间可能是相依的,其相依性在联合分布函数F(t1,…,tn)=P{X1t1,…,Xntn}中体现。联合分布函数还可写作F(t1,…,tn)=K(F1(t1),…,Fn(tn)),其中Fi为Xi的边缘分布函数,K称作它们的分布连接函数。这样写的好处在于元件的寿命特性由其对应的边缘分布表示,而它们之间的相关性只存在于分布连接函数中。最近,文献[13]证明了单调关联系统寿命的分布函数FT与其元件寿命的分布函数Fi的关系,在同分布(可能不独立)条件下有如下表述: 引理5.1令T=φ(X)表示单调关联系统的寿命,其由同分布但可能相依的元件X=(X1,…,Xn)构成。设元件寿命均具有分布函数F,则系统寿命的分布函数 FT(t)=h(F(t)) 其中h称为控制函数,仅与系统结构函数φ和X1,…,Xn的分布连接函数K相关。h在(0,1)上连续且严格递增,满足h(0)=0,h(1)=1。 上结论对分析单调关联系统的性质起关键性作用,基于引理5.1文献[13]分析了多种寿命分布类在单调关联系统中的封闭性,文献[14]证明了多种常用随机序在单调关联系统中的封闭性。最近,文献[15]证明了剩余分位熵(LQE)序在单调关联系统中封闭的条件,其序的意义可参考文献[15]以及其中的引文。接下来本节将证明LQEx序在单调关联系统中封闭的条件,作为LQE序的补对偶,LQEx序的封闭条件与其类似。 定理5.2令X=(X1,…,Xn)和Y=(Y1,…,Yn)为彼此独立但分量可能相依的随机向量,其分量Xi均与X同分布,Yi均与Y同分布。它们分别表示两组元件的寿命。T1=φ(X1,…,Xn),T2=φ(Y1,…,Yn)分别表示由这两组元件组成的结构相同的系统的寿命,它们具有相同的控制函数h, (a)若XLQExY,h是(0,1)上的凸函数,则T1LQExT2; (b)若T1LQExT2,h是(0,1)上的凹函数,则XLQExY。 其中最后一个等式利用变量代换u=h(v),且p′=h-1(p)。 (a)若XLQExY,则由引理1.2可知 对于所有的p′∈(0,1)都成立。又因为h是(0,1)上的增凸函数,故[h′(v)]2在(0,1)上非负递增。于是根据引理3.4可知式大于等于0对于所有的p′∈(0,1)都成立。注意到h在(0,1)上连续且严格递增,满足h(0)=0,h(1)=1,故p=h(p′)∈(0,1)。则由引理1.2可知T1LQExT2。 (b)的证明类似。 注5.3若考虑X1,…,Xn独立同分布且Y1,…,Yn独立同分布的情况。若系统为并联系统,h(x)=xn为凸函数,则由定理5.2(a)可知并联系统保留元件之间的LQEx序。若系统为串联系统,h(x)=1-(1-x)n为凹函数,则由定理5.2(b)可知元件保留串联系统的LQEx序。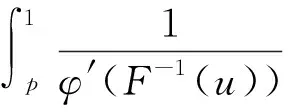
4 LQEx序与试验总时间变量
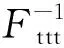
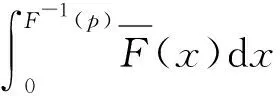

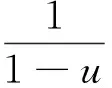


5 单调关联系统中LQEx序的封闭性