一种网格型异构可重构计算系统设计与验证

方 冉， 沈丽娜

(安徽工商职业学院 应用工程学院,安徽 合肥 231131)

引 言

粗粒度可重构体系结构CGRA(coarse grained reconfigurable architectures)在循环内核处理层面具有较高的执行效率和低的功耗消费，传统单核架构在处理计算密集型循环任务时效率低下，在这样的背景下，可重构计算模式被提出，可重构计算目前是国际研究前沿和热点，近三年相关典型的研究列举如下：文献[1]对可重构计算系统的数据流图执行进行了研究，该文针对多缓冲和控制开销问题，提出了一种可重构计算系统优化数据流图执行方法，通过该种方法，获得了计算任务3.4倍的加速[1]。文献[2]针对芯片在指令存储器上消耗能量大的问题，给出了一种基于代码的统计分析方法，同时提出将配置存储器重组为单独分区的硬件/软件协同设计方法，实验结果表明指令解码逻辑所消耗的能量减少了70%[2]。文献[3]对可重构计算系统的容错问题进行了研究，基于三重模块冗余和编码技术的错误检测和纠正理论，该文提出了一个容错模型，实验结果表明任务划分执行效率制约了容错模块恢复时间[3]。文献[4]提出了两种减少可重构系统能量消费的方法，一种是减少配置切换单元的数量；另外一种是减少配置存储器的容量[4]。文献[5]利用程序转换来获得能量和模型性能的权衡，通过一组信号处理和代数内核基准测试表明，该方法获得了50%到80%的资源利用率[5]。文献[6]提出了一种流处理CGRA可重构系统，该系统采用SMIC标准55纳米单元技术，基于7个典型算法，在450MHz的频率下，流处理CGRA平均功耗消费仅为0.84w[6]。文献[7]针对并行数据计算时需要多次访存的问题，提出基于一种CGRA多存储器架构，通过循环基准测试，相对于传统CGRA架构，获得了较好的计算性能改进[7]。文献[8]提出了一种图最小化映射方法[8]。文献[9]给出了粗粒度可重构计算系统的量化评估指标体系，为可重构计算系统的量化评估获得了依据，效果较好[9]。

但是上述工作均是对同构可重构计算系统进行的研究，均没有对异构可重构系统进行设计和同异构可重构系统进行运算分析。如何设计一种异构可重构计算系统？如何结合计算模型来评估异构可重构计算系统显得极为重要。本文对这一问题展开研究。

1 异构可重构计算系统设计与相关定义

为了便于问题研究，下面设计了一种异构可重构计算系统，具体如图1所示：

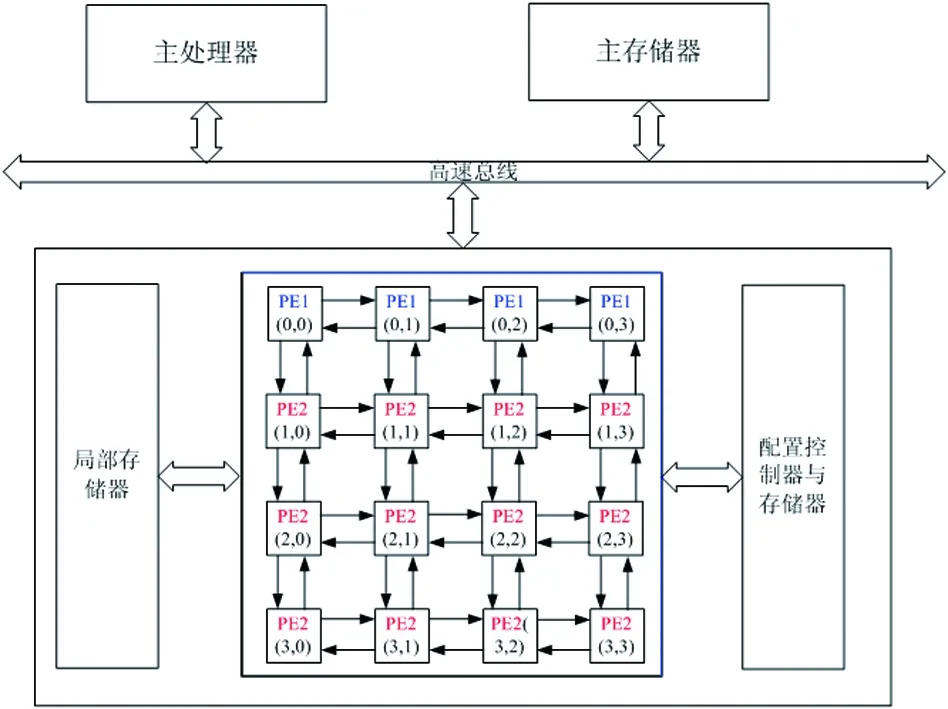
图1 异构可重构计算系统

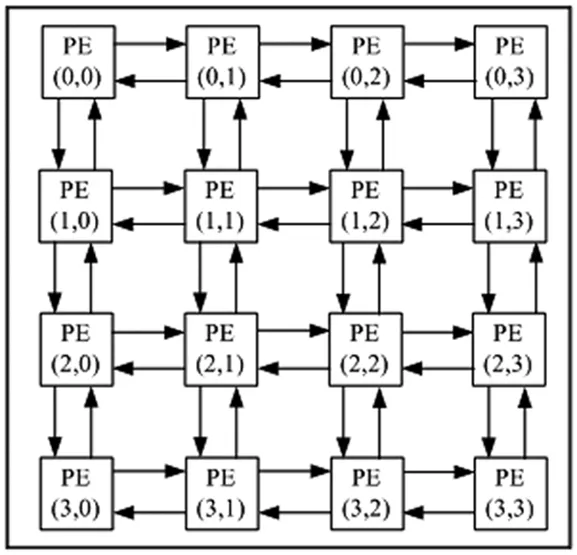
图2 同构可重构处理单元阵列

异构可重构计算系统HRCS(heterogeneous reconfigurable computing system)主要包括主处理器、主存储器，局部存储器，配置控制与存储器，异构可重构处理单元PE(processing element)阵列(说明：图1中PE1类型的单元在处理乘法运算时无需配置，处理其他运算均需要配置，PE2类型的单元可以处理所有的算术逻辑运算)等组件，图形图像等计算密集型任务包含大量矩阵运算，其运算主要乘法和加法的运算，相比较二维无跳变点点近邻互连的mesh结构而言，HRCS具有如下特点：(1)矩阵运算中的乘法运算映射到固定处理单元上，目的是减少重复配置成本；(2)根据设计映射调度算法可以实现行无依赖并行执行。

本文研究的两个前提：(1)针对矩阵及类似的运算。(2)计算平台采用网格型异构可重构计算系统。

本文的主要贡献列举如下：

(1)设计了一种网格型异构可重构计算结构，同时提出了网格加节点GAM(grid add-node mapping)和网格不加节点映射GNM(grid no-add-node mapping)两种任务映射算法，相比较网格型同构可重构计算结构，两种算法在配置成本层面均有减少。

(2)针对网格型异构结构，对比GAM和GNM两种算法，结果发现GAM算法在N1、N2、CCON、TTOTAL等参数方面要优于GNM。

本文要用到的相关定义列举如下：

定义1：可重构异构处理单元阵列RHPEA(reconfigurable heterogeneous processing element array)：设待处理的任务集合V={v1,v2,…,vn}，V=V1∪V2，其中集合V1属于计算密集型任务常用的运算一种类型集合，如矩阵运算的乘法运算等；剩余其他运算V2=V-V1；RHPEA的特征是：用PE1处理集合V1类型的计算并且不需要配置，但是处理V2类型等运算需要配置；用PE2可处理V2类型或V1∪V2类型的运算，每处理一种运算均需要配置，RHPEA就是指包含两类或以上的处理单元(如图1中的PE1和PE2)的阵列。

定义2：可重构同构处理单元阵列RIPEA(reconfigurable isomorphic processing element array)：设待处理的任务集合V={v1,v2,…,vn}，V=V1∪V2，每个PE均可以处理集合V中所有的运算，每处理一种运算均需要配置，处理单元阵列中的每个PE均具有相同的功能，这样的阵列被称为RIPEA。

定义3：RHPEA配置成本弱化：RHPEA中有一类执行单元专门执行有规律频繁出现的次数较多某种运算，如矩阵计算中的乘法运算，通过某一算法把频繁出现的某种运算任务调度到专门的PE，这样PE就不需要配置，直接执行，这样就会节省一定数量的重复配置成本，这种现象称为RHPEA配置成本的弱化，但是RIPEA每个单元在运算前均需要配置。

定义4：网格型CGRA行无依赖映射：设待处理的任务集合V={v1,v2,…,vn}，假设成功映射到CGRA中阵列后的同一行某一任意任务节点vi和vj，i，j∈[1，n]，vi和vj没有前驱和后继的依赖关系，这种情况称为网格型CGRA的行无依赖映射，行无依赖映射可以获得行节点按块运行的并行度的最大化。

定义5：网格型HRCS量化指标体系：本文用到的量化指标体系为配置时间CCON、非原始输入次数N1、非原始输出次数N2、原始输入次数Norg1、原始输出次数Norg2、划分块数M、跨层时延IID(由于网格型结构不允许跨层映射，所以本文的IID=0)、计算任务的执行时延SSD，本文计算任务的执行总时延TTOTAL=CCON+N1+Norg1+N2+Norg2+SSD，具体见文献[9]，限于篇幅，不再累述。

本文研究有两个前提：(1)RHPEA和RIPEA的阵列每块加少量过渡路由节点的个数为2，路由节点可表示为ri，其中i∈[1,n]。(2)每块可重构阵列固定配置时间等参数与文献[9]一致。

2 二维HRCS可调度性分析

2.1 二维HRCS特征分析

二维HRCS具有以下特征：(1)属于片上多核系统，这种结构克服了常用运算重复配置的问题，每个PE单元均可编译程序，其结构及互连形式如图1所示。(2)在主处理器的控制下HRCS完成计算任务的编译，主存储器用来存储计算密集型任务的最后运算结果，局部存储器用来存储中间的运算结果。(3)配置控制与存储器作用是用来生成编译所用的配置字。

2.2 矩阵运算的实例映射分析

实例1：设A为1×4的矩阵，B为4×2的矩阵，矩阵Y=A×B，则

=(i1×i5+i2×i6+i3×i7+i4×i8i1×i9+i2×i10+i3×i11+i4×i12)

(1)

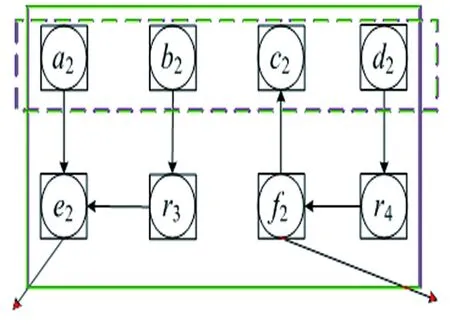
式1的运算控制数据流图DFG(data flow graph)如图3所示：运算任务ai,bi,ci,di,i∈[1,2]均为乘法运算，其执行时间为2cycle，任务ej,fj,gj,j∈[1,2],均为加法运算，其执行时间为1cycle。

一个循环任务子图(见图3)任务间的关系描述见表1，说明本文只讨论图形图像矩阵运算中的循环程序。

基于HRCS平台和行无依赖规则，采用按网格加节点映射GAM和网格不加节点映射GNM两种方法对图3的循环任务进行了映射。

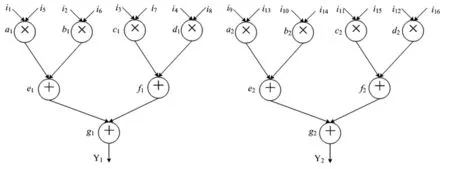
图3 两个循环子图

GAM算法流程：

输入：循环任务图

输出：可执行任务坐标

硬件约束：二维网格型可重构异构或同构处理单元阵列

Step1输入数据表和硬件约束。

Step2扫描就绪列表获得就绪的节点。

表1 循环任务图间顺序关系描述

(1)若是乘法运算，映射的起始行是第一行，然后进行点点加少量过渡节点进行行无依赖映射和列有依赖映射，如第一行放满就转第2行，依次映射；

(2)若不是乘法运算或是乘法运算，但第一行放满了，映射的起始行是第二行，然后进行点点加少量过渡节点进行行无依赖映射和列有依赖映射，如第二行放满就转第3行，依次映射。

Step3若任务点映射没有完成转Step2，否则算法结束。

GNM算法流程：

输入：循环任务图

输出：可执行任务坐标

硬件约束：二维网格型可重构异或同构处理单元阵列

Step1输入数据表和硬件约束。

Step2扫描就绪列表获得就绪的节点。

(1)若是乘法运算，映射的起始行是第一行，然后进行点点不加过渡节点进行行无依赖映射和列有依赖映射，如第一行放满就转第2行，依次映射；

(2)若不是乘法运算或是乘法运算，但第一行放满了，映射的起始行是第二行，然后进行点点不加过渡节点进行行无依赖映射和列有依赖映射，如第二行放满就转第3行，依次映射。

Step3若任务点映射没有完成转Step2，否则算法结束。

若可重构处理单元阵列规模为2×4，分别采用GNM和GAM两种算法获得了图3的两个循环子图映射结果，具体见图4和图5。由图4和图5可知，若采用异构可重构阵列RHPEA，第一行是专用，且为乘法运算，其组合逻辑电路不需要重复配置，a1，b1，c1，d1和a2，b2，c2，d2只需要配置一次。故可以节省4cycle；若采用同构可重构阵列RIPEA，阵列被重复使用时，均需要配置，配置成本为8cycle，从而说明异构可重构阵列RHPEA具有合理性。

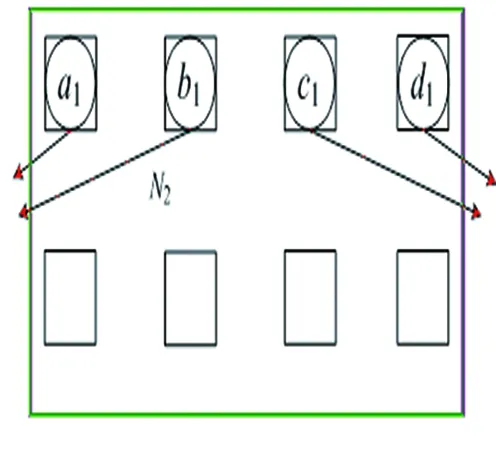
(1)

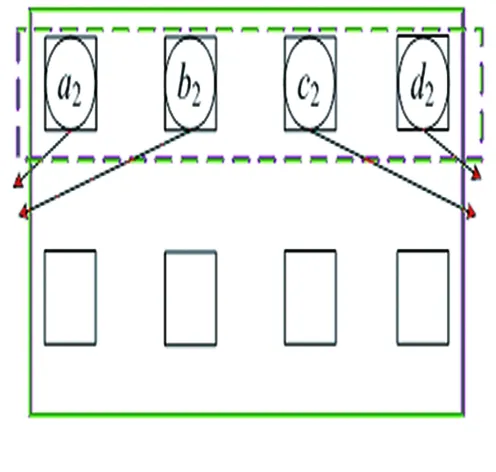
(2)

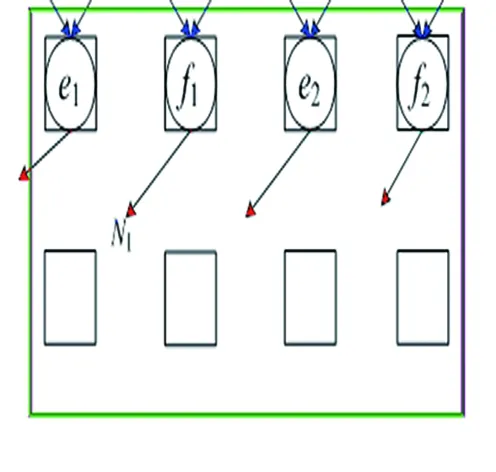
(3)

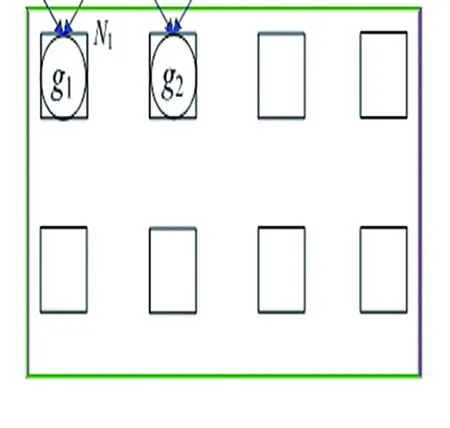
(4)

图4 GNM映射结果

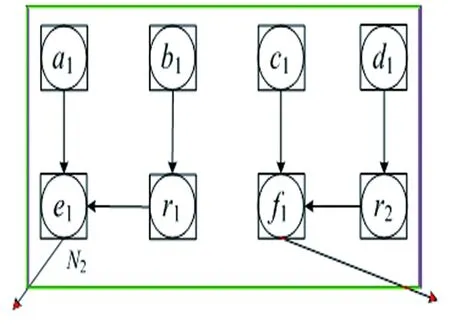
(1)

(2)

(3)

图5 GAM映射结果

图3的循环子图原始输入Norg1=16，原始输出Norg2=2，其他参数的计算方式如定义5所述。

相比较同构RIPEA结构，基于异构RHPEA结构GNM和GAM算法，CCON均节省4cycle，从而说明异构结构具有合理性。相关比较见表2。

2.3 一个4×4矩阵的算例分析

一个4×4矩阵运算展开的数据流循环子图共16个，原始输入Norg1=128，原始输出Norg2=16，若可重构处理单元阵列规模为4×4，基于异构RHPEA架构分别采用GAM和GNM算法获得,实验结果如表3所述。

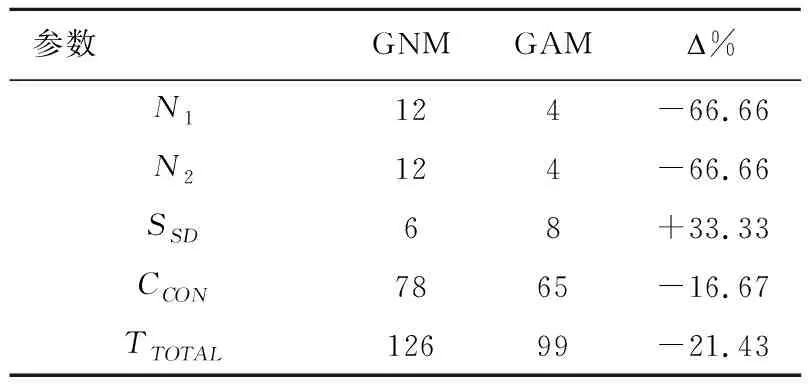
表2 RHPEA结构GAM和GNM映射算法比较

基于4×4矩阵运算，通过算法实验，基于异构RHPEA架构GNM算法的配置时间为219cycle，基于同构RIPEA架构GNM算法的配置时间为231cycle，节省12cycle；基于异构RHPEA架构GAM算法的配置时间为

228cycle，基于同构RIPEA架构GAM算法的配置时间为248cycle，节省20cycle。由此看出，在节省配置时间层面，异构RHPEA架构较具优势。

基于异构RHPEA结构，可重构处理单元阵列规模为4×4，为了进一步验证GAM和GNM算法的优劣，本文采用了更为复杂的例证快速傅立叶变换FFT(fast Fourier transform)4次和8次展开进行实验，实验结果如表4和表5所述：

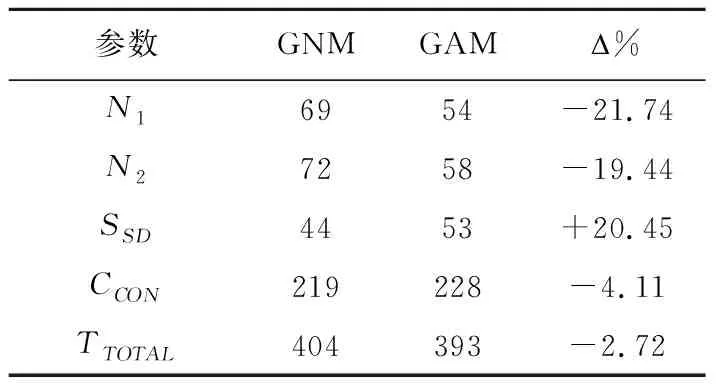
表3 RHPEA结构4×4矩阵运算GAM和GNM算法比较

表4 RHPEA结构FFT4运算的GAM和GNM算法比较

表5 RHPEA结构FFT8运算的GAM和GNM算法比较

分析与小结：针对3.2和3.3节四个算例，由表2-表5可知，针对异构RHPEA，采用了GAM和GNM两种任务映射算法，进行定量分析，发现GAM在N1、N2、CCON、TTOTAL等方面均要优于GNM算法，但是GNM的SSD要优于GAM算法。

3 结 语

本文设计了一种网格型异构可重构计算系统，基于网格加节点映射GAM算法和网格不加节点映射GNM算法对异构可重构计算结构进行了性能评估，结果发现相比较同构网格型可重构计算系统而言，基于一组算例的实验结果可知，网格型异构可重构计算系统具有一定优势。就4×4矩阵运算而言，GAM和GNM算法分别节省配置时间为20cycle和12cycle，同时对比了异构可重构计算系统的GAM和GNM算法，结果表明，相比较GNM算法，GAM算法改进的百分比为2.72%；基于RHPEA结构，相比较GNM算法，GAM在FFT4和FFT8两个较为复杂的测试用例，GAM算法改进的百分比分别为22.8%和18.8%，从而说明了网格型异构可重构计算系统下的GAM算法具有可行性。