双轴各向异性介质表面的Goos-Hänchen位移和Imbert-Fedorov位移

徐靖捷， 黄 辉， 崔玉涵

(北京交通大学 电气工程学院，北京 100044)

引 言

双轴各向异性介质中介电常数和磁导率均为对角张量且对角元互不相等(式(1)、式(2))，电磁波在其中传播时沿各个方向性质不同。学者们对于电磁波在双轴各向异性介质当中的传播进行了大量研究。文献[1]中给出了平面波在双轴各向异性介质中传播时所满足的单叶双曲面形式的色散方程。经过我们的推导，双轴各向异性介质的色散方程为由介质参数所决定的圆锥曲线形式，单叶双曲面形式是其中一种。文献[2]中讨论了双轴各向异性左手材料中平面波的传播特性。左手材料属于双轴各向异性介质范畴,具有的使波的传播方向与其能量传播方向相反的奇特性质，属于双轴各向异性介质的范畴。基于这些研究成果的实际应用也被提出[3]，如分波器、滤波器等等。

(1)

(2)

在这些研究的基础之上，本文关注的重点是双轴各向异性介质表面发生全反射的条件，以及全反射条件下重要的物理现象——Goos-Hänchen(GH)位移和Imbert-Fedorov(IF)位移。

研究发现，当电磁波在介质分界面发生全反射时，反射点会在平行和垂直入射面方向上发生移动，分别称作GH位移和IF位移[4-5]。

产生这两种位移的原因实际上是倏逝波[6]，一种分界面上发生全反射时产生电磁波。其幅值随着垂直分界面方向深度的增加而呈指数衰减。当入射波在介质表面发生全反射时，尽管透射波强度为零，但仍有一部分能量渗透到介质表层(图1中黄色区域)，沿着表面传播一段距离后，再折回到入射介质当中，导致反射点的偏移，进而产生两种位移。

图1 Goos-Hänchen位移和Imbert-Fedorov位移示意图Fig.1 Schematic of Goos-Hänchen shift and Imbert-Fedorov shift

1 理论分析

1.1 全反射条件

倏逝波幅值呈指数衰减是因为全反射时透射波波矢垂直分界面方向分量变为虚数[7]。以两种介质同为各向同性介质为例。

电磁波在介质中传播需满足色散方程(3)，在分界面上需满足相位匹配条件(4)[8]。

(3)

kiy=kry=kty

(4)

根据电磁波矢量满足的式(3)、式(4)，得到图(2)。

aε1μ1>ε2μ2

bε1μ1<ε2μ2

图2 两种各向同性介质分界面上的k表面图

Fig.2 The k surface on the interface between two isotropic mediums

图3 各向同性介质与双轴各向异性介质分界面上的k表面图Fig.3 The k surface on the interface betweenisotropic media and biaxial anisotropic media

如图2a所示，当光由光密介质进入光疏介质(ε1μ1>ε2μ2)。当入射角θi逐渐增大至超过临界角θc后，全反射发生，ktx变为虚数，倏逝波生成进而产生两种位移。而在图2b中光由光密介质进入光疏介质(ε1μ1<ε2μ2)，无论入射角如何变化ktx都为实数，全反射不会发生。

1.2 双轴各向异性介质表面全反射条件

由麦克斯韦方程组，我们可以得到TE波和TM波在双轴各向异性介质当中的色散方程[1]。

(5)

(6)

不同于各向同性介质中色散方程满足圆形，根据式(5)、式(6)，可以看出k表面在双轴各向异性介质当中满足由介质参数决定的圆锥曲线[9]。如图3。

(7)

双轴各向异性介质当中有多种介质参数的组合可以满足这一要求。对式(7)中参数进行讨论得到表1。

表1 TE波在双轴各向异性介质表面全反射条件

我们注意到一些独特现象：在各向同性介质中，我们认为当电磁波从光密介质进入光疏介质且入射角大于临界角后会出现全反射。但在双轴各向异性介质表面我们发现全反射可在任意入射角情况下发生或在入射角小于临界角的情况下发生。对这一条件我们使用COMSOL Multiphysics进行了仿真(μx=0.5,μy=-1,εz=0.5,εx=1,εy=0.9,μz=1,临界角为30°)，发现该现象确实存在(图4)。

入射角25°

入射角45°

图4 双轴各向异性介质表面全反射在入射角小于临界角情况下发生

Fig.4 Total reflection occurs whenθi<θcon the surface of biaxial anisotropic media

图4中所选参数由表1计算可知临界角为30°，分别选择入射角为25°和45°入射。发现45°入射时发生折射，而入射角为25°小于临界角时发生了全反射。

以上仅讨论了TE波发生全反射的条件，由于TE波和TM波的色散方程在双轴各向异性介质当中具有对称性。将参数μx,μy,εz替换为εx,εy,μz即可得到TM波发生全反射的条件。

表2 TM波在双轴各向异性介质表面全反射条件

1.3 双轴各向异性介质表面的GH位移

我们使用稳态相位法来计算TE波在双轴各向异性介质表面发生全反射时产生的GH位移。发生全反射时，入射波与反射波强度相同但相位发生改变。研究发现GH位移的大小与这一相位改变相关。

由色散方程、边界条件和双轴各向异性介质介质参数，我们可以得到TE波的反射系数R[10]，它反映了入射波与反射波幅值和相位间的关系式(8)。

(8)

使用稳态相位法[11]，我们得到了TE波在双轴各向异性介质表面发生全反射时产生的GH位移表达式(9)。

(9)

其中:

(10)

θi为TE波的入射角度。

可以看出当介质参数和入射波角频率确定后，GH位移的大小仅为入射角的函数。

图5 倏逝波产生的IF位移Fig.5 IF displacement generated by the evanescent wave

1.4 双轴各向异性介质表面的IF位移

使用能流法计算IF位移的大小[11]。倏逝波中的能流由坡印廷矢量S表示，如图5所示

根据能流法[12]，IF表达式如下。

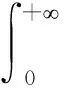
(11)

其中:

Srx是反射波能流x轴分量，Stz是透射波能流z轴分量。

为计算电磁波在各向同性介质和双轴各向异性介质分界面上产生的IF位移，选取入射波为圆极化波。它可以看作是TE波和TM波的叠加。使TE波和TM波同时发生全反射的条件，就是使圆极化波发生全反射的条件。

由圆极化波发生全反射时的电场强度和磁场强度，推导可以得到坡印廷矢量分量的表达式。

(12)

(13)

由式(11)可以得到IF位移的表达式。

(14)

其中:

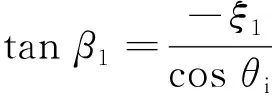
γ为圆极化波的旋向，θi为圆极化波的入射角度。

可以看出当介质参数和入射波角频率确定后，IF位移的大小仅为入射角的函数。

2 结果与讨论

将可以发生全反射的介质参数组合代入GH位移、IF位移的表达式，以期得到不同介质参数条件下入射角与两种位移大小之间的关系。

2.1 GH位移大小随入射角变化规律

图6 GH位移大小随入射角变化规律Fig.6 The relationship between the GH displacement and the incident angle

以表(1)中μxμy>0∩εzμy>0这一情况为例。它可以使全反射在入射角超过临界角的情况下发生，与各向同性介质表面情况近似。发现μx>0,μy>0,εz>0和μx<0,μy<0,εz<0两种介质参数组合均满足这一条件，分别代入式(9)中。

图6展示了GH位移与入射角之间的关系，同时我们还改变了每种关系下的入射波角频率。在这一条件下，位移的大小随着入射角的增大而增大；入射波角频率增大，位移同样增大；位移与入射波波长属同一数量级。这些情况都与各向同性介质上的GH位移类似。

我们还注意到两种介质参数组合所产生的位移大小相等而方向相反。实际上，在包括空气在内的一般介质当中，电磁波的传播方向与其能量传播方向一致，称作右手介质。而在一些特殊的介质参数下，电磁波传播方向将与其能量传播方向相反，此时称介质为左手介质[12]。图6中两种参数恰好对应了两种不同的情况，也导致了产生的GH位移方向相反。图7为示意图。

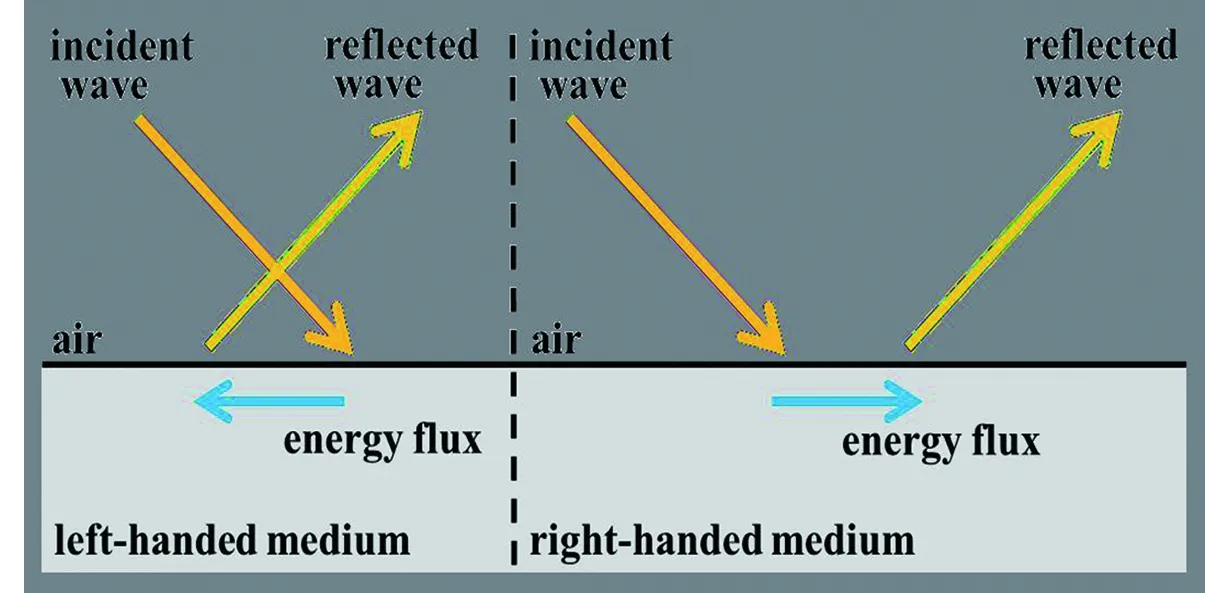
图7 左手介质与右手介质表面的GH位移Fig.7 GH displacements on the surface of left-handed medium and right-handed medium

当电磁波在一般的介质表面发生全发射时，反射点向远离入射波方向移动。然而当电磁波在左手介质表面发生全反射时，由于能量传播方向相反，反射点也将向相反方向移动,导致负的GH位移产生。

2.2 IF位移大小随入射角变化规律

从表1、表2中可以看出，根据介质参数符号的不同，各有四种情况可以使TE波和TM波发生全反射。因此，理论上共16种的介质参数符号组合可以使圆极化波发生全反射。这里我们只选择条件相同的四种情况详细分析。

图8展示了IF位移与入射角之间的关系，我们还改变了每种关系下的介质参数，可以看出左旋极化波与右旋极化波产生的IF位移等大反向,与各向同性介质表面相同。因为双轴各向异性介质表面全反射可在前文所述反常条件下发生，因此IF位移也会在这些条件下产生。相比各向同性介质表面IF位移大小随入射角增大而单调递减，双轴各向异性介质表面IF位移大小随入射角变化规律更为多样。因此，实际上我们可以通过配置介质参数来控制入射角与位移大小之间的关系满足需求。

与各向同性介质相比，双轴各向异性介质的介质参数配置更为多样而灵活，通过设定参数，我们可以使介质实现全新的电磁特性。

μx=0.5,εz=0.5,εx=0.5,μz=0.5

μx=0.8,εz=-0.6,εx=0.8,μz=-0.6

μx=1.2,εz=1.4,εx=1.2,μz=1.4

μx=0.5,εz=0.5,εx=0.5,μz=0.5

图8 IF位移大小随入射角变化规律

Fig.8 The relationship between the IF displacement and the incident angle

3 结 论

本文结合色散关系和相位匹配条件推导了线极化波在各向同性介质与双轴各向异性介质分界面上发生全反射的条件。分别使用稳态相位法和能流法推导出了线极化波产生的Goos-Hänchen位移和圆极化波产生的Imbert-Fedorov位移的解析表达式。对表达式中体现的入射角度、介质参数、入射波角频率等因素进行分析。发现可以通过配置双轴各向异性介质的介电常数和磁导率对位移大小随入射角的变化规律进行调控。文中推导所采用的思路同样适用于其他材料表面发生全反射的条件和GH位移以及IF位移的求取。