基于实值三线性分解的互耦条件下双基地MIMO雷达角度估计算法
杨 康, 文方青, 黄冬梅, 张 磊, 王 可
(1. 中国电子科技集团公司第二十八研究所, 南京 江苏 210007; 2. 空中交通管理系统与技术国家重点实验室, 南京 江苏 210007; 3. 长江大学电子信息学院, 荆州 湖北 434023; 4. 海军指挥学院信息系, 南京 江苏 210016)
0 引 言
伴随着多输入多输出(multiple input multiple output, MIMO)技术在移动通信领域的不断成功与发展,MIMO技术在雷达领域应用的研究方兴未艾。利用匹配滤波处理及虚拟通道的思想,MIMO雷达可获得远优于传统相控阵雷达系统的性能。MIMO雷达技术是学术界、工程界的研究热点之一,该研究方向不仅有重大的理论和学术意义,而且应用前景广阔,特别是具有巨大军事应用价值和民用价值,美、英、日等科技强国均把它作为发展未来智能化探测系统的重点突破的技术[1-3]。为了对敌目标进行有效监测与阻击,需要雷达系统能够快速、精确对敌目标进行定位。角度估计是MIMO雷达目标定位的基本任务之一,因而引起国内外学者的广泛关注。迄今为止,已涌现大量优秀的角度估计算法。典型的MIMO雷达角度估计算法有谱峰搜索法[4]、求根方法[5]、基于旋转不变技术的估计算法[6]、传播算子法[7]、张量方法[8-13]、稀疏表示法[14]等。其中,张量类算法由于能够挖掘MIMO雷达数据的结构相关特性,因而是近几年的研究热点。
然而,上述算法的优异性能均是在理想的阵列条件下获得的。实际上,由于雷达系统往往在非理想的环境下,因而上述算法在实际工程中难以获得理想的性能。阵列MIMO雷达的非理想环境之一是阵元互耦影响,其主要表现为相邻的几个阵元间数据的相互影响。为克服MIMO雷达阵列的互耦效应,已有部分学者开展这方面的研究。文献[15]提出一种基于Capon算法和迭代思想的DOD与DOA及互耦估计算法,文献[16]提出了一种基于降维多重谱峰搜索的算法。上述两种算法均将角度估计转换为二次优化的问题,虽然可有效降低运算量,但是谱峰搜索过程仍然具有较大的复杂量。此外,由于二次优化求解目标角度过程中,阵列受互耦的影响可能会产生模糊效应,因而角度估计的精度可能会严峻下降。利用互耦矩阵的对称Toeplitz结构,文献[17]提出了一种基于旋转不变技术(estimation method of signal parameters via rotational invariance techniques,ESPRIT)的双基地MIMO雷达角度估计算法,通过选择性矩阵可以消去阵列的互耦效应。为利用阵列数据的多维结构,文献[18]提出了一种基于实值高阶子空间分解(higher-order singular value decomposition,HOSVD)算法。文献[19]则提出一种基于三线性分解的DOD与DOA估计算法,其可改善张量分解的精度和计算复杂度。文献[20]采用最小二乘+谱峰搜索的策略进行角度估计,提高了[19]中角度估计的精度,并改善了[19]中的互耦校正的复杂度。文献[21]则提出一种基于张量压缩和稀疏表示的双基地MIMO雷达角度估计算法,该算法仅适合大规模阵列的参数估计,同时会导致参数估计精度的下降。在小规模阵列时,算法可能会完全失效。
考虑到均匀阵列的旋转不变特性和互耦矩阵的Toeplitz对称特性,本文提出一种基于改进三线性分解的双基地MIMO雷达角度估计算法。首先利用选择性矩阵消去阵列互耦效应,然后构建阵列数据的三线性分解模型。考虑到均匀线性阵列(uniform linear array,ULA)的中心对称特性,利用前后平滑技术对张量数据进行处理,再构造阵列的增广输出的三线性分解模型。利用三线性分解获得相关导引矢量的估计,最后再利用阵列的旋转不变特性恢复目标的DOD与DOA。由于三线性分解使用迭代的方式获得相关导引矢量,因而能获得比HOSVD更高的估计精度。且阵列增广输出为实数,故本算法仅涉及实数运算,相比已有复数算法,本文算法的计算复杂度更低。
1 张量基础与信号模型
1.1 张量基础
为方便读者阅读及理解,首先引入文献[22]中关于张量操作的3个定义。
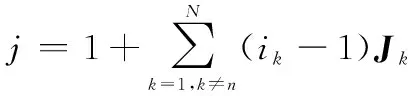
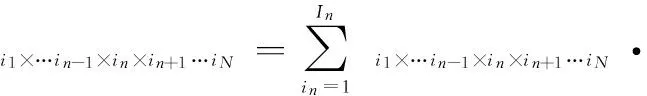
定义3(张量模乘性质):N阶张量X∈CI1×…IN的模乘性质主要有如下两条:
X×n·A×m·B=X×m·B×n·A,m≠n
X×n·A×m·B=X×n·(B·A)
(1)
[X×1·(A1)×2…(AN)]n=
An·[X]n·[AN⊗…An+1⊗An-1…⊗A1]T
(2)
式中,(·)T表示转置。
1.2 信号模型
考虑一个双基地MIMO雷达的阵列模型,如图1所示。

图1 双基地MIMO雷达工作示意图Fig.1 Illustration of bistatic MIMO radar
图1中MIMO雷达的天线系统由M个发射阵元和N个接收阵元构成,二者均是ULA。假设收发阵元间距均为d,为不引起阵列相位畸变需d≤λ/2,λ为发射信号波长,在本文中假设d=λ/2。发射阵元发射相互正交的波形。假设发射天线发射的基带信号为相互正交的编码波形,其中第m(m=1,…,M)路基带信号为sm∈CQ×1,且满足
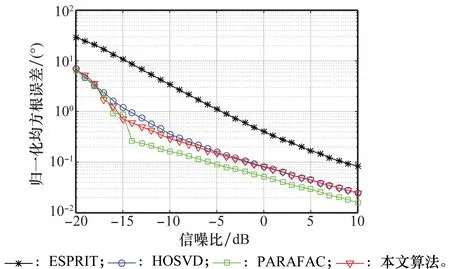
式中,Q为编码码长;(·)H表示共轭转置。假设在雷达远场处于同一个距离元内具有K个目标,第k(1≤k≤K)个目标的方位为(φk,θk),其中为目标的DOD,θk为目标的DOA。假设收、发阵列相邻的P+1个阵元间存在互耦效应,互耦系数分别为cr=[1,cr1,…,crP]T和ct=[1,ct1,…,ctP]T,其中0<|crP|<… 考虑MIMO雷达的一个相干处理时间(coherent processing interval,CPI)包含L个脉冲,则第l(l=1,2,…,L)个脉冲时间的接收阵列的输出信号为 Xl=CrArdiag(bl)(CtAt)TS+Wl (3) (4) (5) 式中,0表示元素全为0的矩阵;I表示单位矩阵;下标均表示矩阵的维数。容易得知[21]: (6) (7) (8) (9) (10) (11) 故通过酉变换后的向量为一个实数向量[18-21]。结合式(10)、式(11)和定义3有 (12) 上述变换后的方向矩阵中含有目标相关信息,如果能获得这些矩阵的估计,则可进一步获得目标参数的相关估计。在传统基于子空间方法的角度估计算法中,往往首先将上述张量转换为矩阵的形式,然后对矩阵进行分解获得目标的信息。这些方法往往无法利用张量数据的多维结构信息,通过张量分解的方式往往能获得更加精确的参数估计性能。现有的张量分解方法主要有两大类:直接法(如HOSVD)和迭代法(三线性分解法)。直接法将张量运算转化为多个子空间分解运算,其计算复杂度往往较大,而迭代法往往通过几次低维的迭代获得高精度的参数估计。三线性分解又称为平行因子分解(parallel factor decomposition,PARAFAC),是一类重要的张量分解方法,本文采用(trilinear alternate least squares,TALS)进行张量分解,具体过程如下节所述。 (13) 式中,E1=[Er]1;E2=[Er]2;E3=[Er]3。式(13)即为三线性分解模型的矩阵表达形式[11],由于Zr中每个索引位置的元素是由3个矩阵的元素的乘积构成,因此可认为Zr具有3个方向。相应地,Z1、Z2和Z3分别可被视为将张量数据Zr沿着发射方向、接收方向和脉冲方向展开而获得的矩阵。传统的子空间分解法往往仅利用了张量的数据的某一个方向展开的信息。 TALS算法是一种高效的三线性分解模算法,其采用最小二乘(least squares,LS)代价函数依次交替的拟合3个矩阵,当拟合误差达到预期范围内时算法终止。其处理本文所述三线性模型的具体步骤如下:①假设Z1、Z2和Z3中的两个矩阵已知,采用LS的方法拟合其中的任何一个矩阵;②采用LS的方法拟合剩下的两个矩阵;③重复①和②直到迭代次数达到预设值或拟合误差达到预设阈值。现以某次具体的迭代过程说明TALS的迭代过程,根据式(13)可知,对Atr拟合的代价函数为 (14) 式中,‖·‖F表示矩阵的Frobenius范数。根据式(14)易知,Atr的LS估计值为 (15) (16) (17) 目标个数K往往是未知的,但是在本文中假设其为一个已知参数,否则其可以利用现有算法进行有效的估计[23]。由于TALS算法在更新过程中Arr、Atr及Br的误差将得到改善或者保持不变,但是不可能增大,因而TALS总是会收敛的[24]。TALS的收敛速度与相关矩阵的初始化优劣密切相关,一般使用随机初始化矩阵将获得较慢的收敛速度,而使用ESPRIT算法可加快算法收敛。此外,使用一些压缩算法可以进一步加快算法收敛。本文在实际仿真中使用COMFAC算法[25],其主要是通过张量压缩的方法降低迭代计算的复杂度,一般仅需若干次迭代算法便可快速收敛。 唯一性是三线性分解的重要特征之一。定理1[26]给出了三线性分解的唯一性的条件: kAtr+kArr+kBr≥2K+2 (18) (19) 式中,Ω是一个列置换矩阵;N1,N2和N3分别对应的估计误差矩阵;Δ1,Δ2和Δ3为3个对角矩阵,其对角元素分别表示相应的尺度因子,且其满足Δ1Δ2Δ3=IK。 (20) 式中,Ψt=diag(gt);Ψr=diag(gr);gt=[gt1,gt2,…,gtK]T;gr=[gr1,gr2,…,grK]T;gtk=tan(πsinφk/2);grk=tan(πsinθk/2),k=1,2,…,K。其他旋转性矩阵分别为 (21) (22) 综上所述,现将本文算法的具体流程可以总结如下: 步骤1将接收数据按照式(5)排列成一个三维矩阵; 步骤2按照式(7)进行去耦运算,按照式(10)构造前后平滑的数据张量Zc,进一步按照式(11)获得经过酉变换的实数张量Zr; 步骤4按照式(21)获得gtk、grk(k=1,2,…,K),并按照式(22)获得DOD与DOA的估计值。 表1 各种算法复杂度的比较 本文算法相比传统算法的优势主要体现在如下几个方面: (1) 能有效应对收发阵列存在互耦的场景,且无需额外的校准源; (2) 无需奇异值分解,无需谱峰搜索; (3) 自动匹配所估计的DOD与DOA; (4) 三线性分解仅涉及实数运算,计算复杂度低; (5) 对相干源仍然适用。 场景1收发阵元弱互耦干扰背景,P=1,互耦系数分别为ct=[1,0.117 4+j0.057 7],cr=[1,-0.012 1-j0.102 9]; 场景2收发阵元强互耦干扰背景,P=2,互耦系数分别为ct=[1,0.8+j0.5,0.2+j0.1],cr=[1,0.6+j0.4,0.1-j0.3]。 图2是在SNR=-15 dB、场景1、非相干源条件下本文算法进行200次蒙特卡罗仿真的散点图,图3是在SNR=-10 dB、场景2、相干源(目标一和目标二的相干度为0.99)条件下本文算法200次蒙特卡罗实验的散点图。可以看出,两种仿真条件下3个目标的可以清楚的被估计出来,并且被正确配对,因而本算法对非相干源和相干源均适用。 图2 场景1非相干源背景下本文算法估计的散点图Fig.2 Scatter results of the proposed method in case I with non-coherent sources 图3 场景2相干源背景下本文算法估计的散点图Fig.3 Scatter results of the proposed method in case II with coherent sources 图4与图5分别为所有算法在场景1、非相干源、不同信噪比条件下所提算法RMSE和PSD性能的对比。由图4可知,在低信噪条件下,张量算法性能较为接近,但性能均优于ESPRIT算法。随着信噪比增加,所有算法的性能均有所提高,但本文算法在信噪比较低时性能优于HOSVD算法,在高信噪比条件下性能接近HOSVD。同时,所提算法性能会劣于PARAFAC,这是由本文算法在最后估计过程中存在孔径损失造成的。由图5可知,所有算法的PSD在高信噪比时都会达到100%。随着信噪比的降低,PSD会下降,其开始下降所对应的信噪比位置被称为信噪比阈值[17]。可以看出,但使用了张量计算的算法信噪比阈值要低于ESPRIT。此外,所提算法的PSD性能在信噪比低于阈值时优于HOSVD但劣于PARAFAC。 图4 场景1非相干源条件下RMSE性能比较Fig.4 RMSE comparison in case I with non-coherent sources 图5 场景1非相干源条件下PSD性能比较Fig.5 PSD comparison in case I with non-coherent sources 图6与图7分别为所有算法在场景2、非相干源、不同信噪比条件下所提算法RMSE和PSD性能的对比。对比图4、图5中的相关曲线可知,强互耦环境下相关算法的性能均有所下降。但是本文算法的RMSE性能与PSD性能仍处于HOSVD与PARAFAC之间,但仍然远优于ESPRIT算法。考虑到本文所提算法在计算复杂度方面具有很大的优势,因而本文所提算法可获得估计精度和估计复杂度方面的折衷。 图6 场景2非相干源条件下RMSE性能比较Fig.6 RMSE comparison in case II with non-coherent sources 图7 场景2非相干源条件下PSD性能比较Fig.7 PSD comparison in case II with non-coherent sources 图8和图9分别为所有算法在在场景2、相干源、不同信噪比条件下所提算法RMSE和PSD性能的对比,其中第1个目标和第2个目标的相干度为0.99。可以看出,ESPRIT算法和PARAFAC算法均不能有效的分辨出相干源,而HOSVD算法和本文算法此时均能够有效工作。此外,本文算法在低信噪比条件下性能优于HOSVD算法,在高信噪比条件下性能与HOSVD方法非常接近。综合考虑到本文算法的复杂度低于HOSVD方法,本文算法要优于HOSVD方法。 图8 场景2相干源条件下RMSE性能比较Fig.8 RMSE comparison in case II with coherent sources 图9 场景2相干源条件下PSD性能比较Fig.9 PSD comparison in case II with coherent sources 本文提出了一种基于实值三线性分解的互耦条件下双基地MIMO雷达联合DOD与DOA估计算法。构建了接收数据的张量模型,利用均匀阵列的中心对称特性和酉变换构造实值张量数据的增广输出,并将参数估计转换为实值三线性分解问题。最后通过阵列旋转不变方法估计目标方位。所提算法能有效应对相干源,并具有较小的计算复杂度。最后,在详细分析算法性能的基础上对算法性能进行了仿真分析和比较。 [1] 何子述,韩春林,刘波,等.MIMO雷达概念及其技术特点分析[J].电子学报, 2005, 33(12): 2441-2445. HE Z S, HAN C L, LIU B, et al. MIMO radar and its technical characteristic analyses[J].ACAT Electronica Sinica, 2005, 33(12): 2441-2445. [2] 陈浩文, 黎湘,庄钊文. 一种新兴的雷达体制—MIMO雷达[J]. 电子学报, 2012, 40(6): 1190-1198. CHEN H W, LI X, ZHUANG Z W. A rising radar system-MIMO radar[J]. ACAT Electronica Sinica, 2012, 40(6): 1190-1198. [3] 王珽, 赵拥军, 胡涛.机载MIMO雷达空时自适应处理技术研究进展[J]. 雷达学报, 2015, 4(2): 136-148. WANG T, ZHAO Y J, HU T. Overview of space-time adaptive processing for airborne MIMO radar[J]. Journal of Radars, 2015, 4(2): 136-148. [4] YAN H, LI J, LIAO G. Multitarget identification and localization using bistatic MIMO radar systems[J]. EURASIP Journal on Advances in Signal Processing, 2008(1): 283483. [5] 谢荣, 刘峥. 基于多项式求根的双基地MIMO雷达多目标定位方法[J]. 电子与信息学报, 2010, 32(9):2197-2200. XIE R, LIU Z. Multi-target localization based on polynomial rooting for bistatic mimo radar[J]. Journal of Electronics & Information Technology, 2010, 32(9): 2197-2200. [6] DUOFANG C, BAIXIAO C, GUODONG Q. Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12): 770-771. [7] ZHENG Z D, ZHANG J Y. Fast method for multi-target localisation in bistatic MIMO radar[J].Electronics Letters,2011,47(2): 138-139. [8] ZHANG X, XU Z, XU L, et al. Trilinear decomposition-based transmit angle and receive angle estimation for multiple input multiple output radar[J]. IET Radar, Sonar & Navigation, 2011, 5(6):626-631. [9] LI J F, ZHOU M. Improved trilinear decomposition-based method for angle estimation in multiple input multiple output radar[J]. IET Radar, Sonar & Navigation, 2013, 7(9): 1019-1026. [10] CHENG Y, YU R, GU H, et al. Multi-SVD based subspace estimation to improve angle estimation accuracy in bistatic MIMO radar[J]. Signal Processing, 2013, 93(7): 2003-2009. [11] WEN F Q, XIONG X D, SU J, et al. Angle estimation for bistatic MIMO radar in the presence of spatial colored noise[J]. Signal Processing, 2017, 134, 261-267. [12] WEN F Q, ZHANG Z J, ZHANG G, et al. A tensor-based covariance differencing method for direction estimation in bistatic MIMO radar with unknown spatial colored noise[J]. IEEE ACCESS, 2017, 5(1): 18451-18458. [13] XU B Q, ZHAO Y B, CHENG Z F, et al. A novel unitary PARAFAC method for DOD and DOA estimation in bistatic MIMO radar[J]. Signal Processing, 2017, 138: 273-279. [14] LI J, ZHANG X. Sparse representation-based joint angle and Doppler frequency estimation for MIMO radar[J]. Multidimensional Systems and Signal Processing, 2015, 26(1):179-192. [15] 刘志国, 廖桂生. 双基地MIMO雷达互耦校正[J]. 电波科学学报, 2010, 25(4):663-667. LIU Z G, LIAO G S. Mutual coupling calibration for bistatic MIMO radar systems[J]. Chinese Journal of Radio Science, 2010, 25(4):663-667. [16] LIU X L, LIAO G S. Direction finding and mutual coupling estimation for bistatic MIMO radar[J]. Signal Processing, 2012, 92(2):517-522. [17] ZHENG Z D, ZHANG J, ZHANG J Y. Joint DOD and DOA estimation of bistatic MIMO radar in the presence of unknown mutual coupling[J].Signal Processing,2012,92(12): 3039-3048. [18] WANG X P, WANG W, LIU J, et al. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling[J]. Signal Processing, 2015, 116:152-158. [19] WEN F Q, XIONG X D, ZHANG Z J. Angle and mutual coupling estimation in Bistatic MIMO radar based on PARAFAC decomposition[J]. Digital Signal Processing, 2017, 65: 1-10. [20] WEN F Q, ZHANG Z J, WANG K. Angle estimation and mutual coupling self-calibration for ULA-based bistatic MIMO radar[J]. Signal Processing, 2018, 144: 61-67. [21] WANG X H, ZHANG G, WEN F Q, et al. Angle estimation for bistatic MIMO radar with unknown mutual coupling based on three-way compressive sensing[J]. Journal of Systems Engineering and Electronics, 2017, 28 (2):1-9. [22] KOLDA T G, BADER B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455-500. [23] DI A. Multiple source location-a matrix decomposition approach[J]. Transactions on Acoustics,Speech and Signal Processing,1985, 33(5): 1086-1091. [24] SIDIROPOULOS N D, BRO R, GIANNAKIS G B. Parallel factor analysis in sensor array processing[J]. IEEE Trans.on Signal Processing, 2000, 48(8): 2377-2388. [25] BRO R, SIDIROPOULOS N D, GIANNAKIS G B. A fast least squares algorithm for separating trilinear mixtures[J].Proc Ica’99 Aussois, 2015. [26] JIANG T, SIDIROPOULOS N D. Kruskal’s permutation lemma and the identification of CANDECOMP/PARAFAC and bilinear models with constant modulus constraints[J]. IEEE Trans.on Signal Processing, 2004, 52(9): 2625-2636.


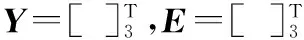
2 基于实值三线性分解的联合角度估计算法
2.1 阵列去耦合



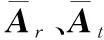
2.2 实值张量模型


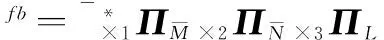
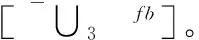
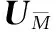

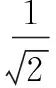

2.3 TALS


2.4 联合DOD与DOA估计




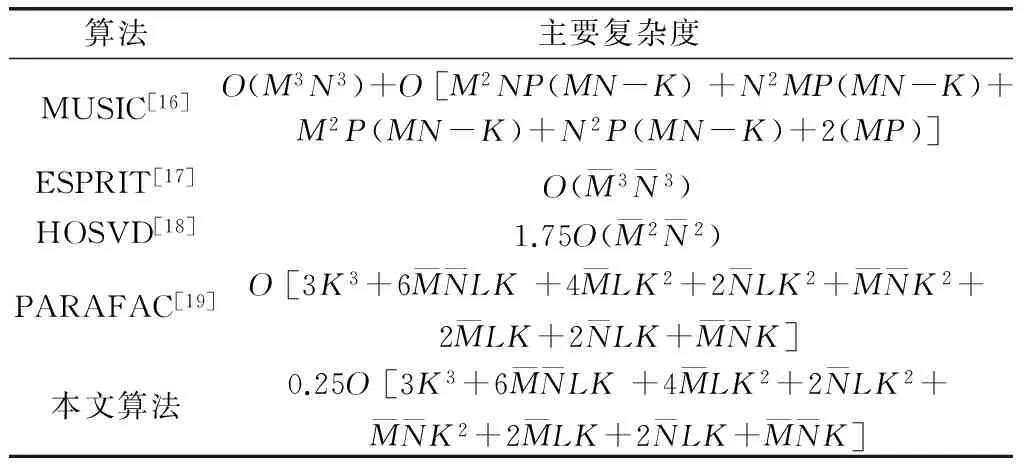
3 算法分析
3.1 复杂度分析

3.2 可辨识度分析

3.5 算法优势分析
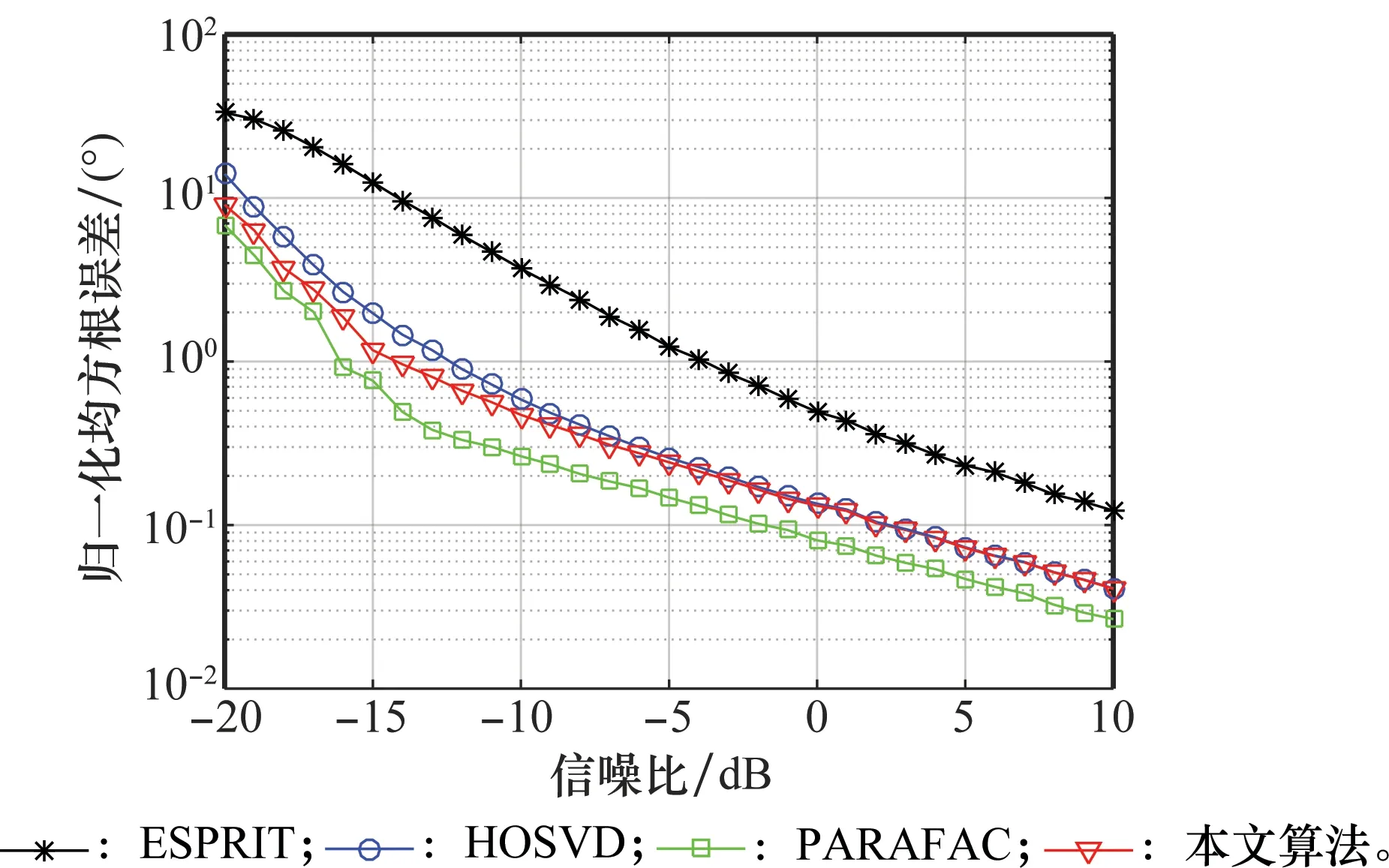
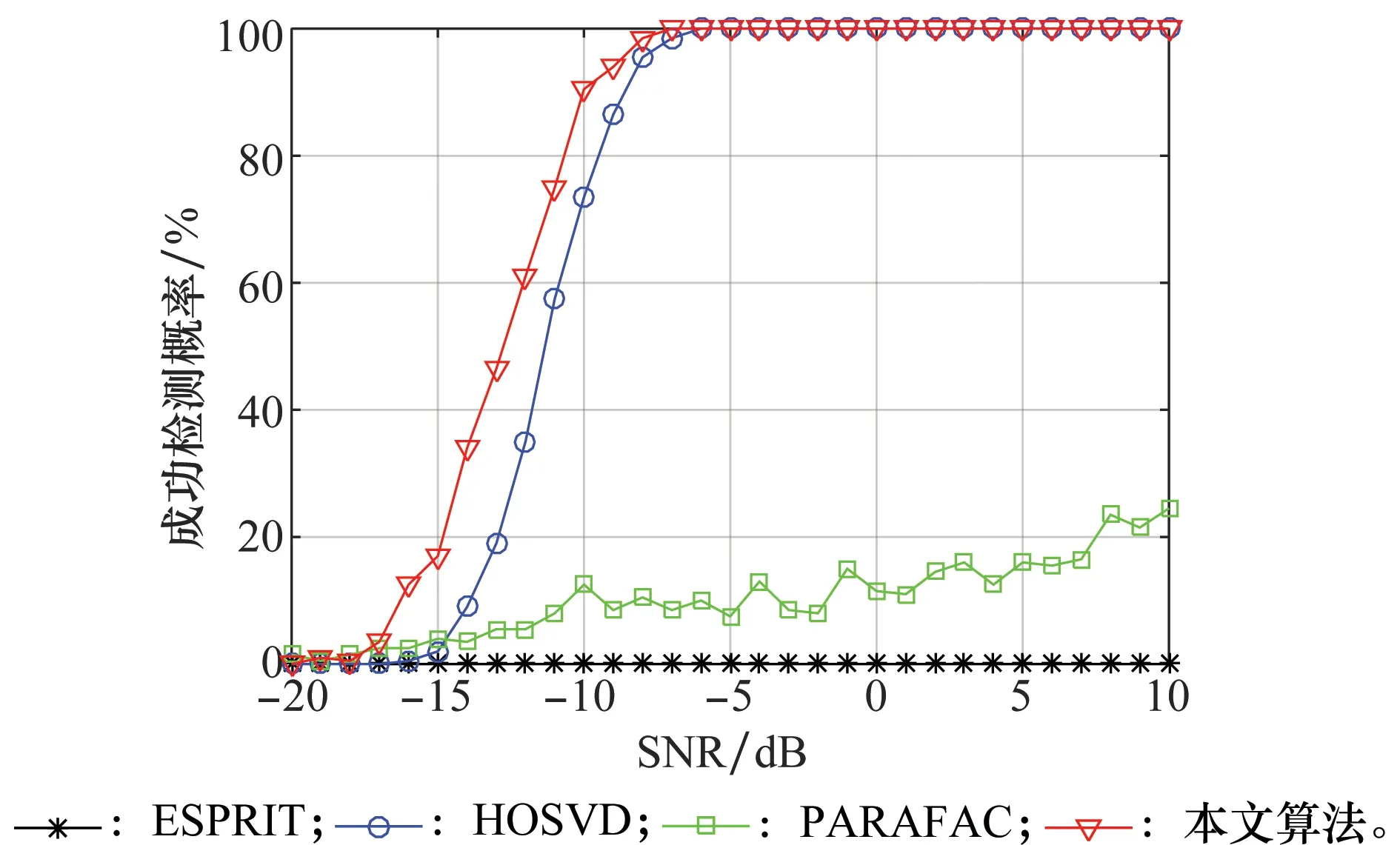
4 仿真结果及分析







5 结 论

