基于主成分约简和突变级数的舰载机出动能力综合评估方法

夏国清, 栾添添, 孙明晓, 仲伟东, 刘彦文

(1. 哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001;2. 中国船舶工业集团公司第708研究所, 上海 200011)

0 引 言

航母是现代海上作战的重要组成,随着世界各国对领海安全的重视,研究航母作战能力成为新的热点。航母作战能力主要体现为舰载机的出动能力[1-3]。研究对比不同作战方案的舰载机出动能力有利于最终作战方案的确定[4-5]。因此,评估舰载机出动能力具有重要的理论意义和应用价值。

由于影响舰载机出动能力的因素数量多且关系复杂,因此评估的重点在于权重系数的确定。通常,对于复杂系统的评估,采用主观的层次分析法(analytic hierarchy process, AHP),通过专家评分获得最终的评估结果。文献[6]提出了萤火虫算法-层次分析算法,从全局对判断矩阵的一致性进行检验,对AHP中各要素的排序权值进行全局最优求解,实现算法参数少、求解简单、收敛速度快的目的。文献[7]考虑在确定综合评价指标相对权重的过程中,采用改进的可拓层次分析法与动态加权法有机结合的方法,既能够解决同类型指标权重难以确定的问题,又能够综合考虑专家的个体差异及人为判断的柔性因素对评价结果造成的主观影响。文献[8]提出一种新的相对基偏好表示方法,在多个等级上同时刻画成对方案间的优于、劣于、无差异和不确定4种关系。文献[9]整合了层次分析法和模糊综合评价法。文献[10]利用模糊层次分析法解决了多准则决策模型问题。文献[11]基于欧洲质量管理基础提出了一种结合模糊逻辑、层次分析法和业务研究方法。然而,这些评估方法主观性和片面性较强,容易忽略较多评估指标之间的相关性和矛盾性等联系,因此难以对多元评估对象进行全面客观地评价。

由于舰载机出动能力指标较多,各个指标之间可能存在一定的相关性,而指标间相关将对评估对象产生重复信息。而主成分约简法能够从众多相关的指标中约简出相互独立的指标,并且保证约简后数据信息损失最小。文献[12]提出基于Lp-模的稀疏主成分分析降维方法,通过极大化带有稀疏正则项的Lp-模样本方差,使得其在降维的同时保证了稀疏性和鲁棒性。文献[13]根据主成分分析法的降维去噪技术和核独立成分分析法的盲源分离技术,提出了一种关于两者的融合方法。文献[14]提出一种基于互信息的主成分分析特征选择算法,该算法计算特征间的互信息,以互信息矩阵的特征值作为评价准则确定主成分的个数,并衡量主成分分析特征选择的效果。文献[15]在粒子滤波框架下,提出了一种基于概率主成分分析表观模型的视觉跟踪算法。文献[16]提出一种新的空间稀疏数据的主成分分析预测方法。文献[17]利用主成分分析法和模糊决策树解决分类问题。

突变级数法没有对指标采用权重,但它考虑了各评估指标的相对重要性,从而减少了主观性又不失科学性、合理性,而且计算简单准确。文献[18]将突变级数理论应用于矿场顶板安全分类中。文献[19]将粗糙集理论与突变级数理论相结合来分析土地生态过程。文献[20]将突变级数法和指标偏离度思想相结合提出基于突变级数法的障碍诊断模型。

本文利用主成分约简方法结合突变级数方法(principal component reduction and sudden change progression method, PCR-CPM)对舰载机出动能力进行客观评估,避免传统的评估方法主观性较强和评估过程复杂的特点,本文主要结构如下:首先,确定舰载机出动能力指标体系的层次结构;其次,利用主成分约简方法将具有相关性的原始指标转换成相互独立的主分量;然后,利用突变级数方法对相互独立的主分量进行评估计算;最后,通过与传统的评估方法进行比较,验证新的综合评估方法的有效性和可靠性。

1 舰载机出动能力指标

目前,国内对于航母的使用经验很少,作为理论研究,借鉴国外相关研究成果来指导评估指标体系的建立。利用递归层次法建立具有层次性、相关性和矛盾性的三级评估指标体系。图1总结了国外常用的舰载机出动能力评估指标[1-3]。

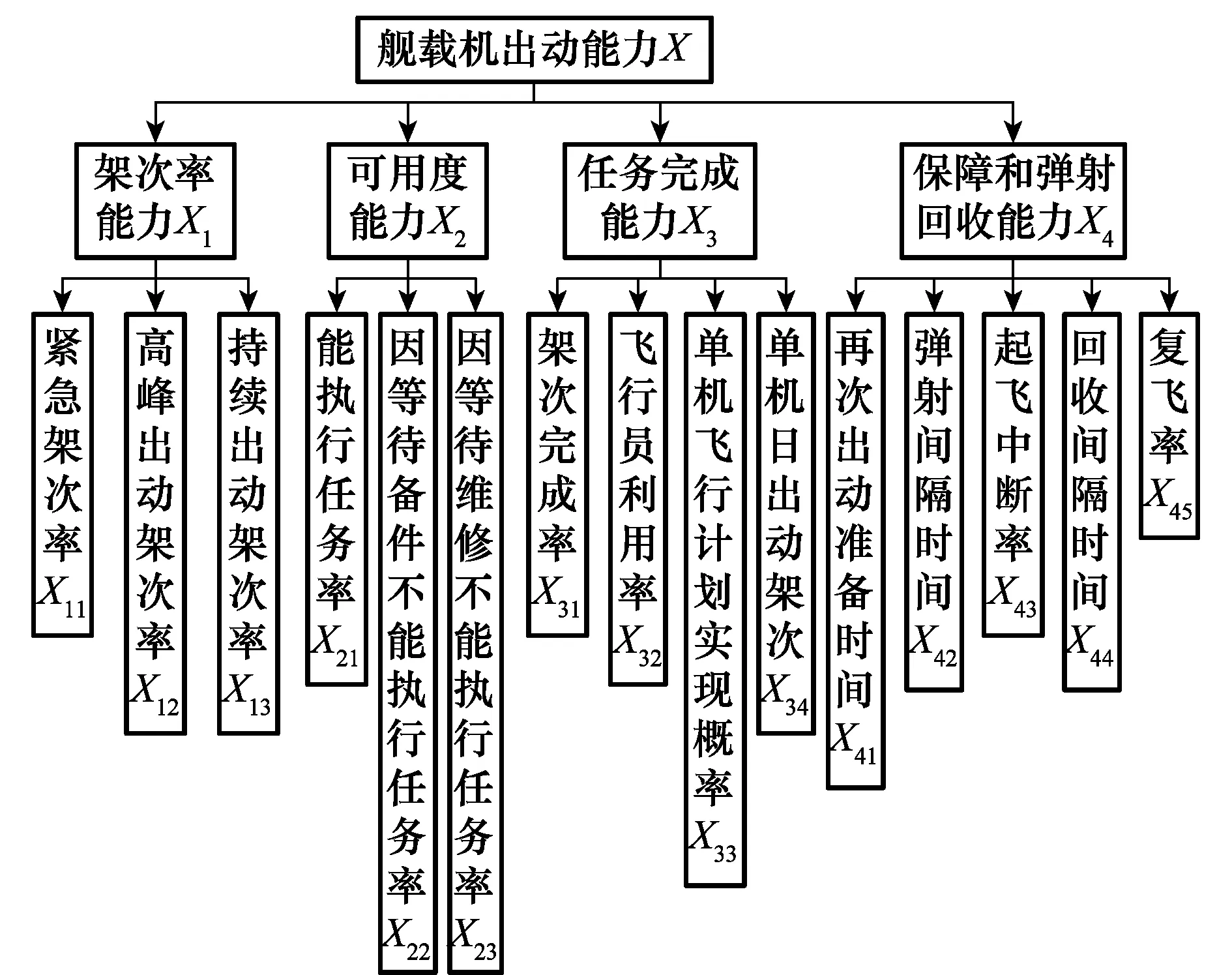
图1 指标体系Fig.1 Index system

各个指标定义如下:

(1) 紧急架次率(单位:架次):按一定的战备警戒等级,在几分钟或十几分钟内,已经准备好起飞的舰载机以最快速度能起飞的数量。

(2) 高峰出动架次率(单位:架次/天):航母在短时间内(4天)高强度出动时,平均一天出动的架次。

(3) 持续出动架次率(单位:架次/天):航母在持续作战时间内(30天),平均一天能出动的架次。

(4) 能执行任务率(单位:%):在一定的飞行计划和后勤维修供应能力条件下,舰载机至少能执行一项规定任务的时间所占的比例。

(5) 因等待备件不能执行任务率(单位:%):由于等待供给系统的备件而不能执行任务的舰载机所占的比例。

(6) 因等待维修不能执行任务率(单位:%):由于维修原因(正在维修或等待维修人员)使舰载机处于故障状态的时间所占的比例。

(7) 架次完成率(单位:%):按计划完成出动的架次占原计划出动架次的比例。

(8) 飞行员利用率(单位:次/天):指飞行员平均每天的使用次数,包括:顺利起飞的架次,备用架次,以及起飞中断的架次。

(9) 单机飞行计划实现概率(单位:%):在一定的约束条件下,在给定时间内,单架舰载机能实现飞行计划的概率。

(10) 单机日出动架次(单位:架次/天):在一定的约束条件下,单架舰载机每天为完成特定任务而起飞、飞行和着舰的架次数。

(11) 再次出动准备时间(单位:分钟):在一定资源配置条件下,舰载机降落后准备再次出动所需要的时间。

(12) 弹射间隔时间(单位:分钟):单部弹射器弹射一架飞机所需的平均时间。

(13) 起飞中断率(单位:%):起飞前因故障或其他原因终止起飞的架次占所有预飞架次的比例。

(14) 回收间隔时间(单位:分钟):回收一架舰载机所需要的平均时间。

(15) 复飞率(单位:%):进场的舰载机未能成功着舰而复飞的次数占舰载机总进场次数的比例。

2 主成分约简方法

2.1 主成分约简原理

由于舰载机出动能力指标较多,各个指标之间可能存在一定的相关性,而指标间相关将对评估对象产生重复信息。利用主成分约简法,能够从众多相关的指标中约简出相互独立的指标,并且保证约简后数据信息损失最小。

主成分约简通过比较各个指标的贡献值确定指标的重要程度。

2.2 主成分约简步骤

主成分约简步骤如图2所示。

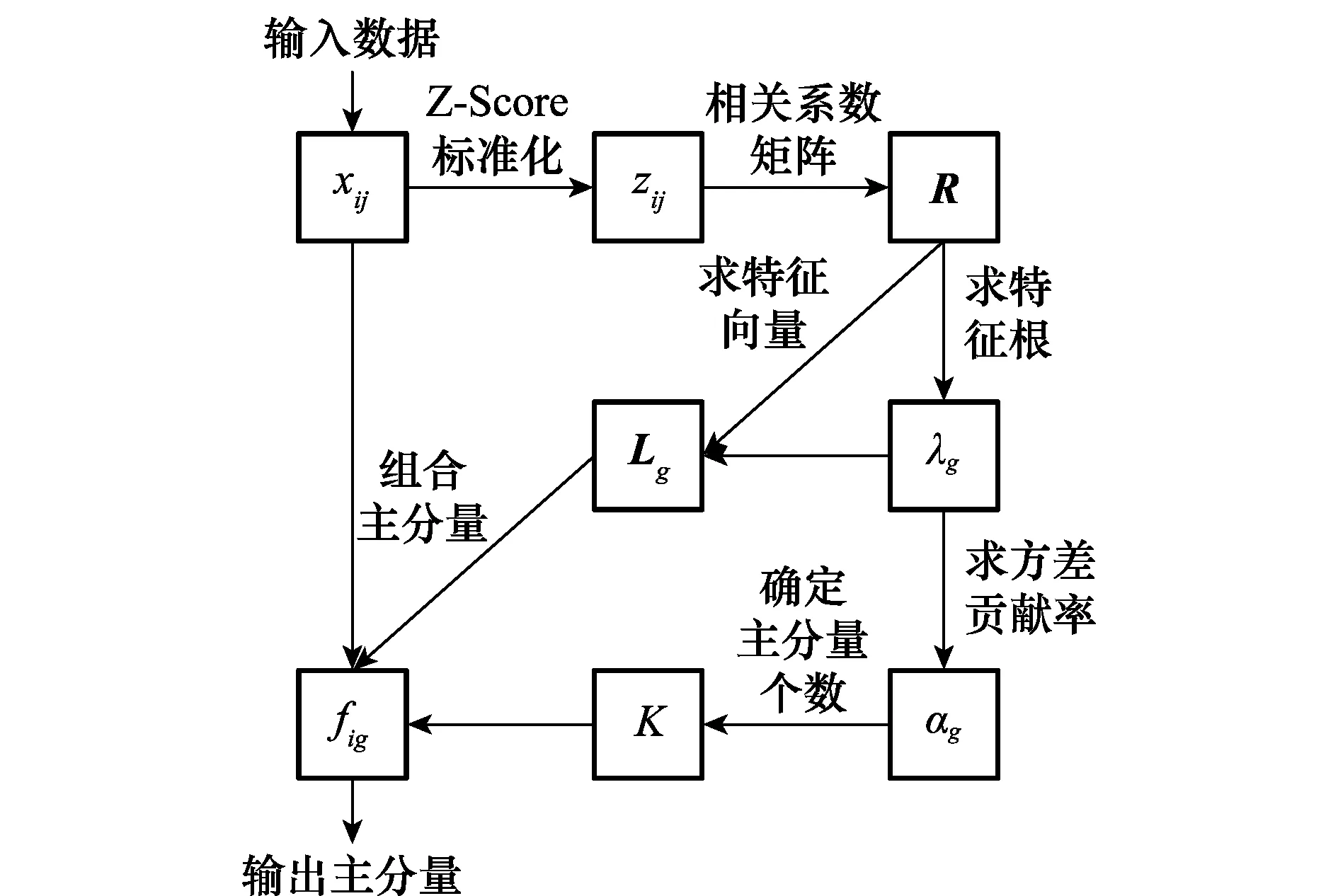
图2 约简过程Fig.2 Process of reduction

具体步骤如下:

步骤1指标参数标准化

由于各个指标的量纲不同,存在不可公度性问题,需要对各个指标进行无量纲化处理,通过数值变换来消除指标间的量纲影响。对于原始数据矩阵X=[xij]n×m,n为对象数量,m为指标数量,采用Z-Score法对指标进行标准化处理为Z=[zij]n×m:

(1)

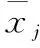
步骤2确定指标之间的相关系数矩阵R

R=[rjk]m×m,rii=1

rjk=rkj

(2)

步骤3确定R阵的特征根

R的特征方程为

|λgIm-R|=0

(3)

式中,λg(g=1,2,…,m)为特征根,表明分量的重要性。

步骤4确定R阵的特征向量

由方程组求特征向量

[λgIm-R]Lg=0

(4)

式中,L是m维实向量。

步骤5确定R阵的贡献率

αg为贡献率,其表达式为

(5)

步骤6确定主分量的个数K

将各个分量按照贡献率大小排序,如果原始个数较多,则取前K个代表所有分量。

(6)

根据α(K)≥95%确定主分量个数。

最终可以将m个相关指标约简为K个不相关的主分量fi1-fiK。

(7)

经过约简之后的指标体系如图3所示。

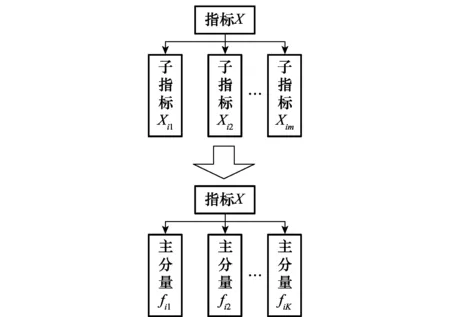
图3 约简后指标体系Fig.3 System after reduction

3 突变级数评估方法

3.1 突变级数评估描述

在制定舰载机作战方案的过程中,需要从多个备选方案中快速选出最优方案。按照突变级数法,所得突变级数化为0-1的数,突变级数越大的方案较好。

3.2 突变级数评估步骤

突变级数方法步骤如图4所示。

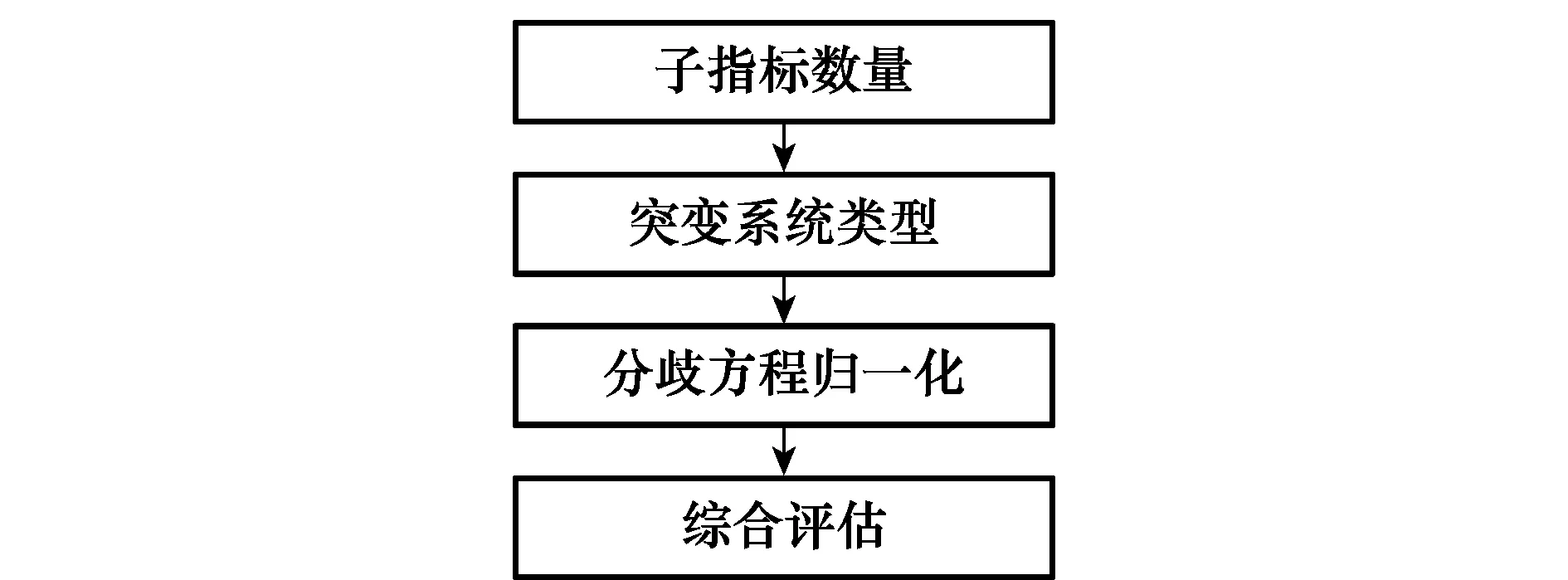
图4 突变级数评估过程Fig.4 Evaluation process with catastrophe progression method

步骤1确定突变评估指标体系的突变系统类型

根据指标的子指标数量确定突变系统模型,如表1所示。表1中势函数是7种初等突变类型的常见的3种,根据一个指标可以分解的子指标个数确定突变函数。如果可分解为2个子指标,系统可视为尖点突变系统。如果可分解为3个子指标,系统可视为燕尾突变系统。如果可分解为4个子指标,系统可视为蝴蝶突变系统。

表1 突变系统

表1中,f(x)为一个指标x的势函数;a,b,c和d为子指标,重要性从高到低。

步骤2归一公式

通过对势函数f(x)求一阶倒数得到临界点,其表达式为

f′(x)=0

(8)

通过对势函数f(x)求二阶倒数得到奇点,其表达式为

f″(x)=0

(9)

将x消掉,求出归一公式。

步骤2.1尖点突变系统分解形式的分歧点集方程为

a=-6x2,b=8x3

(10)

化为突变模糊隶属函数,即如下归一公式：

xa=a1/2,xb=b1/3

(11)

式中,xa为对应a的x值;xb为对应b的x值。

步骤2.2燕尾突变系统分解形式的分歧点集方程为

a=-6x2,b=8x3,c=-3x4

(12)

化为突变模糊隶属函数,即如下归一公式：

xa=a1/2,xb=b1/3,xc=c1/4

(13)

步骤2.3蝴蝶突变系统分解形式的分歧点集方程为

a=-10x2,b=20x3,c=-15x4,d=4x5

(14)

化为突变模糊隶属函数,即如下归一公式：

(15)

归一公式实质上是一种多维模糊隶属函数。

步骤3综合评估

当存在多种方案时,取每个方案的目标为A1,A2,…,Am,则最优结果为

C=A1∩A2∩…∩Am

(16)

相应的隶属函数为

μ(x)=μA1(x)∧μA2(x)∧…∧μAm(x)

(17)

式中,μAi(x)为Ai的隶属函数,为最小目标值。

4 舰载机出动能力评估

4.1 舰载机出动能力评估样本

选取“尼米兹”航母在1997年的高强度演习为评估对象[1],为保证主成分约简的科学性,随机抽取10个方案作为样本,数据如表2～表5所示。

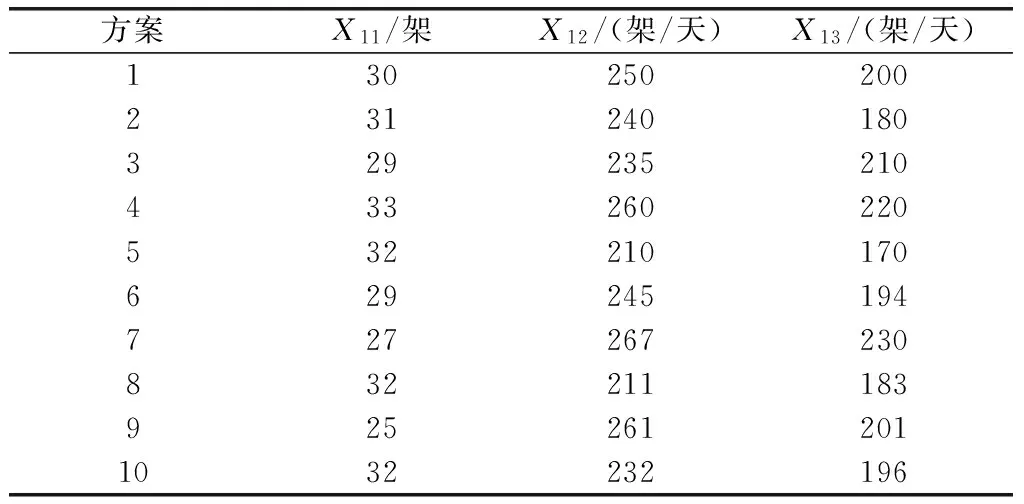
表2 架次率能力指标

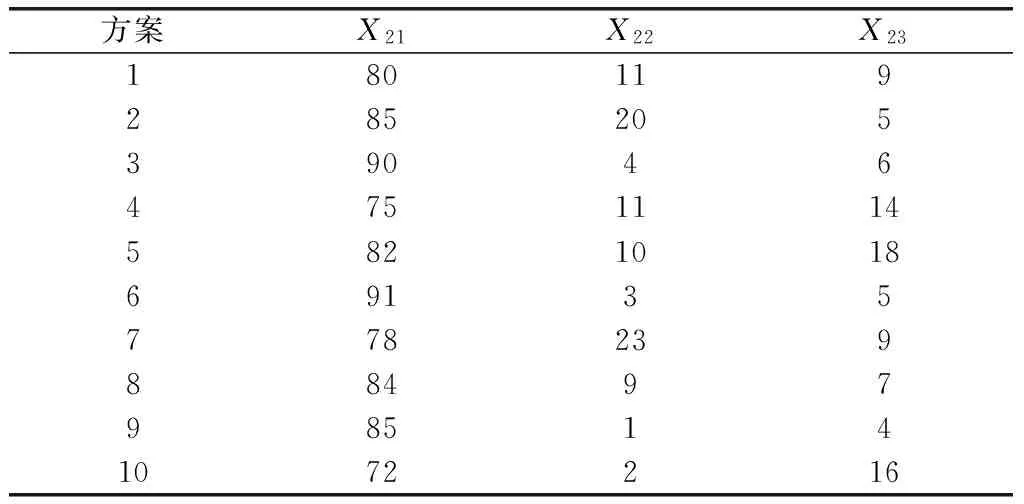
表3 舰载机可用度能力指标

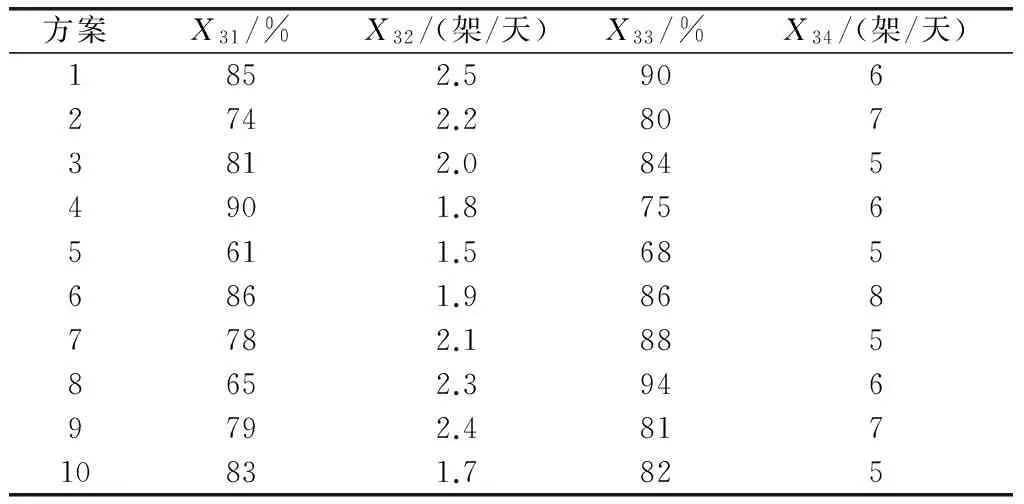
表4 任务完成能力指标

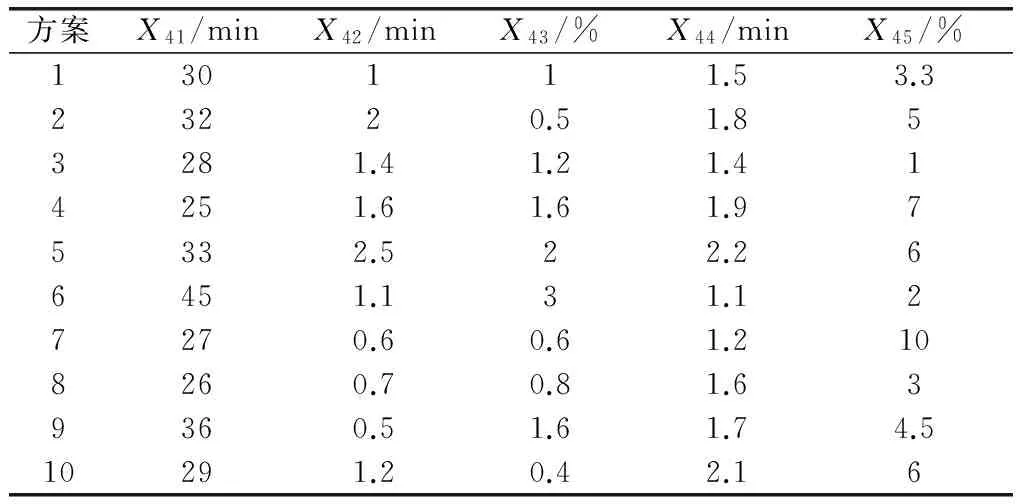
表5 保障和弹射回收能力指标

4.2 指标约简

以保障和弹射回收能力X4指标的主成分约简为例。

步骤1标准化

采用Z-Score法进行标准化,结果如图5所示。

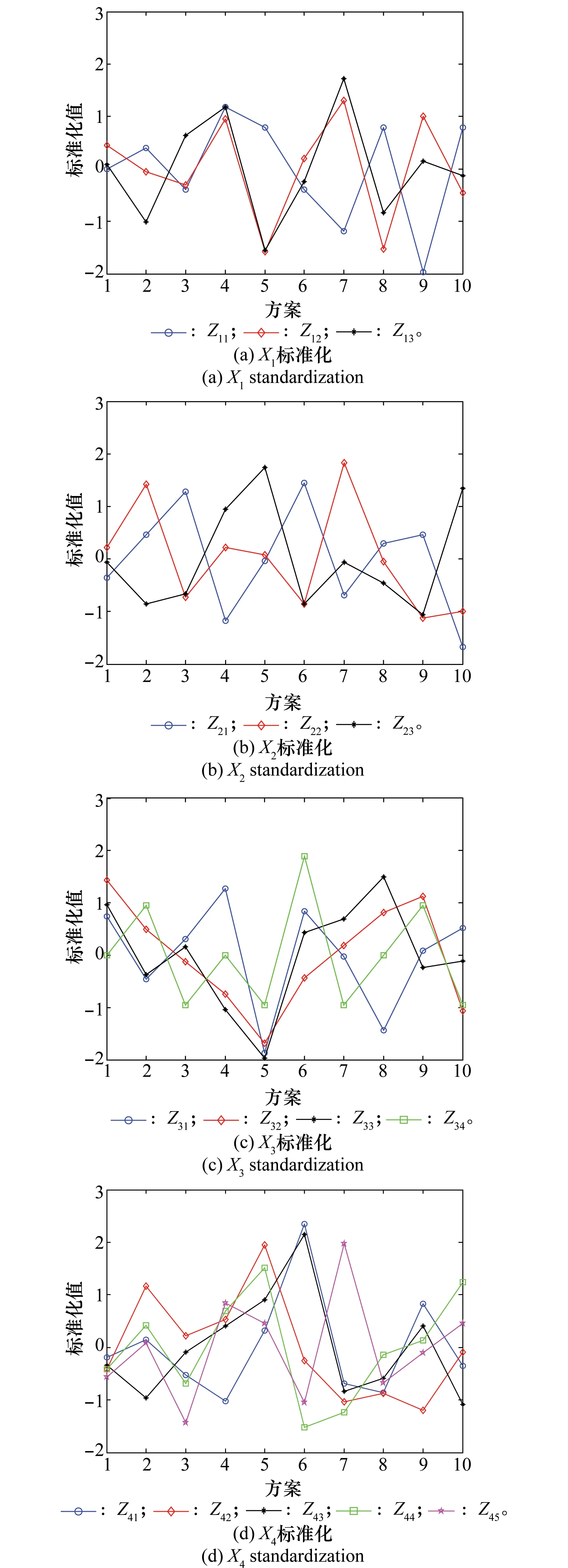
图5 X标准化Fig.5 Standardization of X

步骤2指标数据间的相关系数矩阵

R=

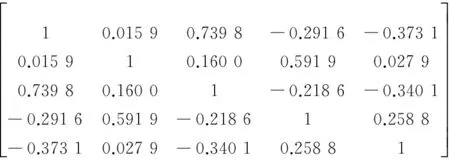
(18)

步骤3相关系数矩阵特征根

(19)

步骤4相关系数矩阵特征向量

(20)

步骤5计算贡献率

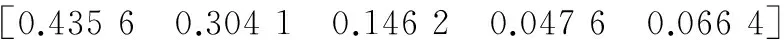
(21)

步骤6确定主分量个数

取α(K)≥95%,将α按照由大到小顺序排列:

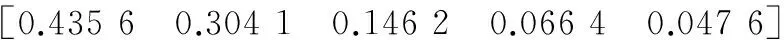
(22)

当K=4时,α(K)=95.24%≥95%。

步骤7确定约简主分量

由特征根、特征向量和主分量个数最终确定保障和弹射回收能力X4指标的约简主分量f41、f42、f43和f44:

(23)

同理,重复步骤1～步骤7,可以确定架次率能力X1指标、舰载机可用度能力X2指标和任务完成能力X3指标的约简主分量:

(24)

(25)

(26)

由式(23)～式(26)和贡献率,可得到综合得分模型:

(27)

根据式(27)可知各个子指标的重要性,权重确定图如图6所示。

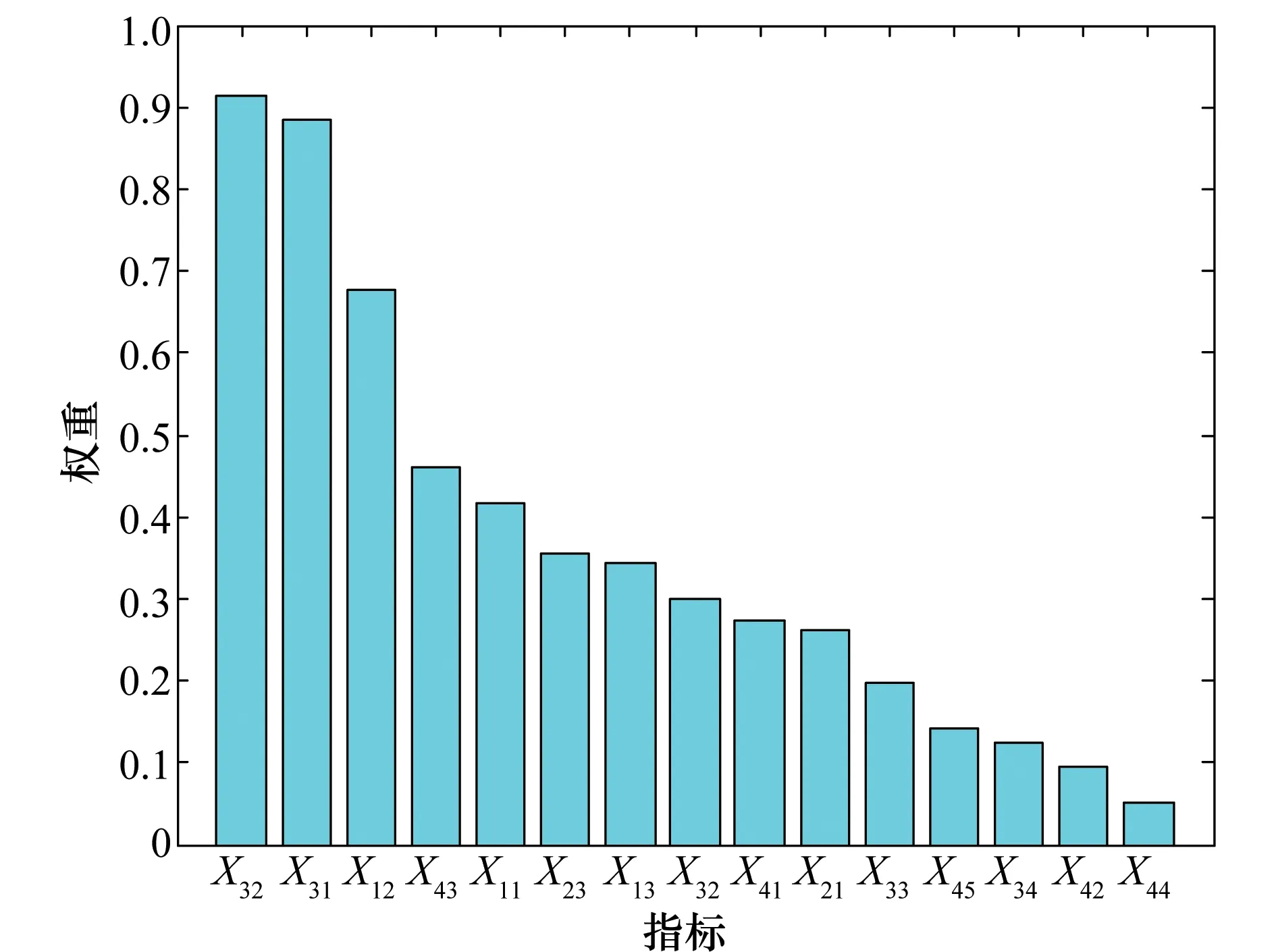
图6 主成分分析权重Fig.6 Weights of principal components

从图6中可以直观了解各个子指标的重要性的高低。同时,由图6可知,最重要的子指标为飞行员利用率和架次完成率,其指标权重远大于其他指标的权重。

4.3 突变级数评估

约简后的指标体系如图7所示。

突变级数评估步骤:

步骤1计算约简主分量评估值并归一化

以架次率能力X1指标的主分量f11,f12和f13的归一化为例,结果如表6所示。

图7 约简后指标体系Fig.7 Reduced system

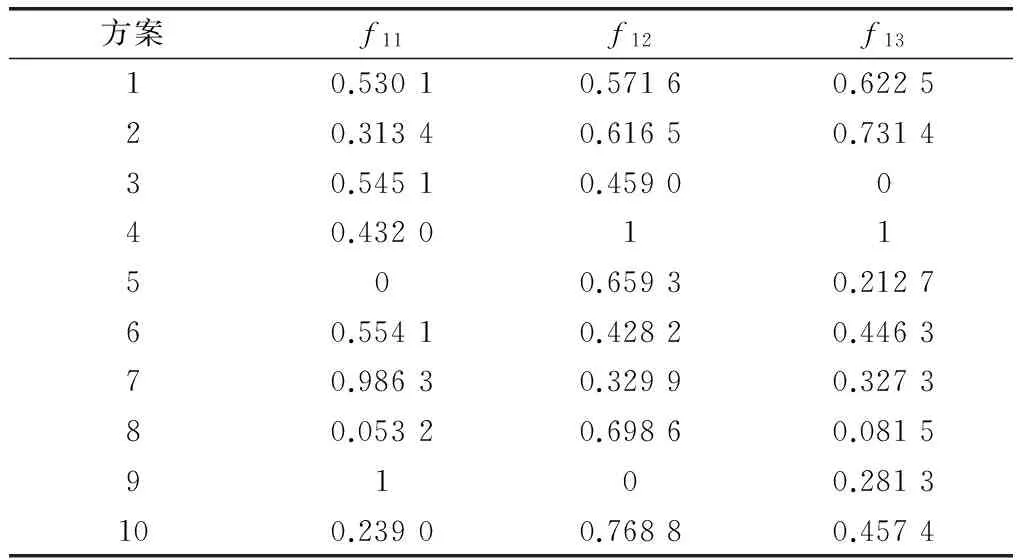
方案f11f12f1310.53010.57160.622520.31340.61650.731430.54510.4590040.432011500.65930.212760.55410.42820.446370.98630.32990.327380.05320.69860.08159100.2813100.23900.76880.4574

步骤2根据突变类型,计算评估值

计算指标X1,X2,X3和X4突变级数评估值。由于X1和X2子指标个数为3,突变类型为燕尾型。由于X3和X4子指标个数为4,突变类型为蝴蝶型。因此，计算评估值如表7所示。

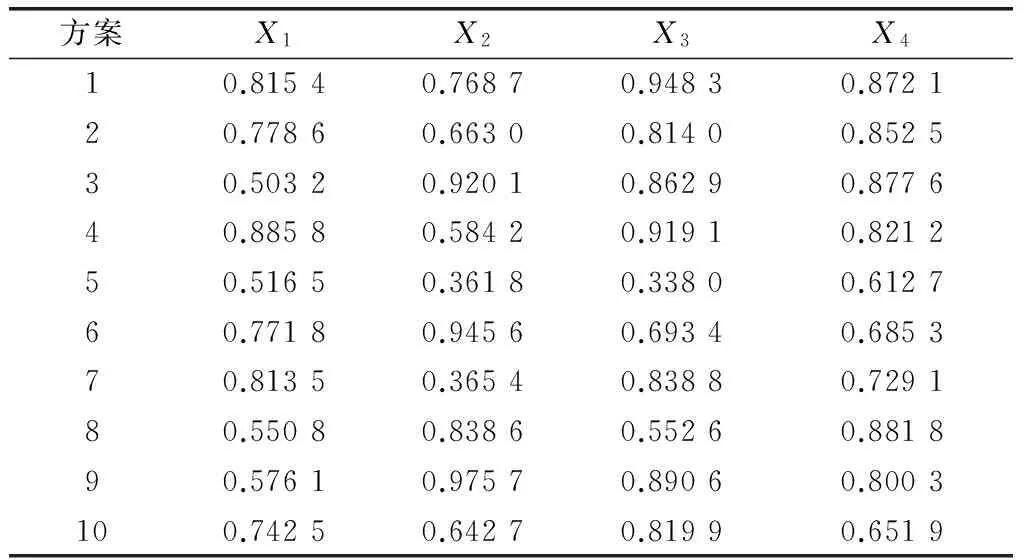
表7 指标X4突变级数评估值

步骤3计算X评估值

由于指标X子指标个数为4,突变类型为蝴蝶型,最终10个方案的评估结果如表8所示。

表8 指标X突变级数评估值

4.4 综合评估结果分析

为了验证基于主成分约简和突变级数评估方法的有效性,将本文提出的PCR-CPM评估结果与文献[10]的模糊AHP(fuzzy AHP, F-AHP)评估结果进行对比,如图8所示。两种评估结果的偏差如图9所示。

图8 评估结果对比Fig.8 Evaluation comparison

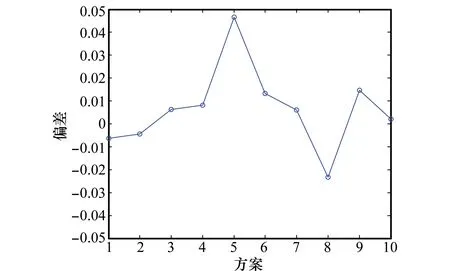
图9 评估结果的偏差Fig.9 Evaluation deviations

由图8和图9可知,基于主成分约简和突变级数评估结果与AHP评估结果基本一致,说明基于主成分约简和突变级数评估方法是有效可靠的,同时避免了AHP评估方法的依靠专家的主观赋权问题,能够较为客观地评估方案的优劣。

对于方案5的评估,AHP的评估结果为0.667 8,本文所提方法的评估结果为0.623 3,AHP的评估结果较高,而方案5中持续出动架次率为170架/天,与其他方案相比最低,因等待维修不能执行任务率为18%,与其他方案相比最高,剩余指标与其他方案相近,通过分析可知持续出动架次率和因等待维修不能执行任务率是较为重要的两个指标,因此这个方案的评估值应与其他方案的评估值差距较大,AHP的评估结果显示其与方案3的结果接近,这是由于主观赋权时只体现了指标之间哪个更为重要,但是指标之间的差距大小受主观影响可能存在与实际结果不符的情况。而本文所提方法避免了主观影响对结果造成的影响,更为客观可信。

因此,所选的10个方案的优劣可以根据综合评估值确定,结果如图10所示。

图10 方案优劣排序Fig.10 Scenarios order

由图10可知,10个方案中最好的方案为方案4,综合评估值为0.971 9,最差的方案为方案5,综合评估值为0.623 3。

因此,基于主成分约简和突变级数综合评估方法实现了对舰载机出动能力的指标重要性分析和方案排序,保证了评估的客观性、可靠性和快速性。

5 结 论

本文给出了基于主成分约简和突变级数的舰载机综合评估方法,得到以下结论:

(1) 在确定舰载机出动能力指标体系的基础上,针对指标之间的高度相关性的特点,采用主成分约简方法,将相关的指标转换成相互独立分量,消除了评估指标之间的相关关系的影响,并根据贡献度确定主分量。

(2) 利用突变级数法对约简后的主分量进行评估,方法简易,不用权重,大大减少了评估的主观性,同时,突变级数法实际上是一种多维模糊隶属函数,适合于矛盾的多目标评估决策问题,解决了传统的评估方法对矛盾的目标难以处理的问题。

(3) 利用主成分约简和突变级数法相结合的方法,实现对舰载机出动能力的两级综合评估。实现了对舰载机出动能力的指标重要性分析和方案排序,保证了评估的客观性、可靠性和快速性。当已知每个指标的实际取值范围时,可以利用本文所提方法在该范围内获得最优方案。

基于主成分约简和突变级数的评估方法可用于其他具有强相关性或矛盾性的复杂系统的评估,简化评估过程。

[1] ANGELYN J, MAUREEN A W, COLLEEN M K G, et al. USS nimitz and carrier airwing nine surge demonstration[D]. Alexandria: Center for Naval Analyses, 1998.

[2] JEWELL A. Sortie generation capacity of embarked airwings[D]. Alexandria: Center for Naval Analyses, 1997.

[3] PATTEN M P. Forecasting carrier air-wing operational availability with event step simulation[D]. Monterey: Master thesis of Naval Postgraduate School, 1999.

[4] XIA G Q, LUAN T T, SUN M X. Evaluation analysis for sortie generation of carrier aircrafts based on nonlinear fuzzy matter-element method[J]. Journal of Intelligent and Fuzzy Systems, 2016, 31(6): 3055-3066.

[5] XIA G Q, LUAN T T, SUN M X, et al. Research on modeling of parallel closed-loop support process for carrier aircraft based on system dynamics[J]. International Journal of Control and Automation, 2016, 9(11): 259-270.

[6] 范阳涛,汪民乐,文苗苗,等.基于萤火虫算法-层次分析法的弹道导弹突防效能分析[J].系统工程与电子技术,2015,37(4): 845-850.

FAN Y T, WANG M L, WEN M M, et al. Analysis of ballistic missile penetration effectiveness based on FA-AHP[J]. Systems Engineering and Electronics, 2015, 37(4): 845-850.

[7] 高炜, 张庆普, 敦晓彪, 等. 基于改进的可拓层次分析法和动态加权的航天高技术综合评价研究[J]. 系统工程与电子技术, 2016, 38(1): 102-109.

GAO W, ZHANG Q P, GUO X B, et al. Comprehensive assessment of advanced military aerospace technologies based on improved EAHP and dynamic weighting[J]. Systems Engineering and Electronics, 2016, 38(1): 102-109.

[8] 付超, 侯震. 基于多等级方案成对比较的决策方法[J]. 控制与决策, 2015, 30(10): 1828-1834.

FU C, HOU Z. Decision method based on pairwise comparison of alternatives on multiple grades[J]. Control and Decision, 2015, 30(10): 1828-1834.

[9] NGUYEN H T, DAWAL S Z M, NUKMAN Y, et al. An integrated approach of fuzzy linguistic preference based AHP and fuzzy COPRAS for machine tool evaluation[J]. Plos One, 2015, 9: 1-24.

[10] SALIMI N, REZAEI J. Multi-criteria university selection: formulation and implementation using a fuzzy AHP[J]. Journal of Systems Science & Systems Engineering, 2015, 24(3): 1-23.

[11] EZZABADI J H, SARYAZDI M D, MOSTAFAEIPOUR A. Implementing fuzzy logic and AHP into the EFQM model for performance improvement: a case study[J]. Applied Soft Computing, 2015, 36(C): 165-176.

[12] 李春娜, 陈伟杰, 邵元海. 鲁棒的稀疏Lp-模主成分分析[J]. 自动化学报, 2017, 43(1): 142-151.

LI C N, CHEN W J, SHAO Y H. Robust spare Lp-norm principle component analysis[J]. Acta Automatica Sinica, 2017, 43(1): 142-151.

[13] 梁胜杰, 张志华, 崔立林, 等. 基于主成分分析与核独立成分分析的降维方法[J]. 系统工程与电子技术, 2011, 33(9): 2144-2148.

LIANG S J, ZHANG Z J, CUI L L, et al. Dimensionality reduction method based on PCA and KICA[J]. Systems Engineering and Electronics, 2011, 33(9): 2144-2148.

[14] 范雪莉, 冯海泓, 原猛. 基于互信息的主成分分析特征选择算法[J]. 控制与决策, 2013, 28(6): 915-919.

FAN X L, FENG H H, YUAN M. PCA based on mutual information for feature selection[J]. Control and Decision, 2013, 28(6): 915-919.

[15] 张辉, 赵保军. 基于概率主成分分析表观模型的视觉跟踪[J]. 系统工程与电子技术, 2009, 31(12): 2826-2829.

ZHANG H, ZHAO B J. Visual tracking based on probabilistic PCA appearance model[J]. Systems Engineering and Electronics, 2009, 31(12): 2826-2829.

[16] JANDAROV R A, SHEPPARD L A, SAMPSON P D, et al. A novel principal component analysis for spatially misaligned multivariate air pollution data[J].Journal of the Royal Statistical Society,2016, 66(1): 3-28.

[17] VARMA K V S R P, RAO A A, MAHALAKSHMI T S, et al. A computational intelligence technique for the effective diagnosis of diabetic patients using principle component analysis(PCA) and modified fuzzy SLIQ decision tree approach[J]. Applied Soft Computing, 2016, 49: 137-145.

[18] CHEN H J, LI X B, LIU A H. Classification of stope roof safety based on catastrophe progression method and its application[C]∥Proc.of the 7th International Symposium on Rockburst and Seismicity in Mines, 2009: 195-202.

[19] CAO W, ZHOU S L, WU S H. Land-use regionalization based on landscape pattern indices using rough set theory and catastrophe progression method[J]. Environmental Earth Sciences, 2015, 73(4): 1611-1620.

[20] 陈晓红,杨立.基于突变级数法的障碍诊断模型及其在中小企业中的应用[J].系统工程与电子技术,2013,33(6):1479-1485.

CHEN X H, YANG L. Obstacle diagnosis model based on the catastrophe progression method and its applications for the small and medium-sized enterprises[J]. Systems Engineering and Electronics, 2013, 33(6): 1479-1485.