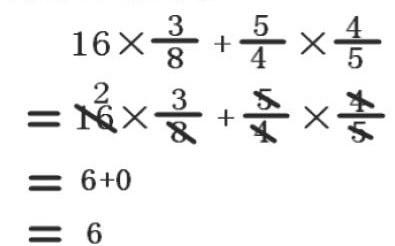教师操作演示规范的重要性

季艳秋

数学是思维的体操，小学生思维发展的基本特点是以具体形象思维为主要形式逐步过渡到抽象逻辑思维为主要形式。但是这种抽象逻辑思维在很大的程度上仍然是直接与感性经验相联系的，仍然具有很大成分的具体形象性。由于数学知识的抽象性和学生思维现状之间存在矛盾，所以我们在教学时需要为学生创设问题情境，赋予数学知识丰富的内容与形式，设计一些直观演示和操作活动，让学生动眼、动脑、动手、动口多种感官协作，通过观察、操作等方式，使物质的外部操作过渡到智力的内部认识活动，从形象到表象再到抽象，培养学生的思维能力，促使认识内化，使学生形成良好的认知结构。

在教学活动中，教师规范的操作演示对学生新知的形成起着重要的作用教师的规范操作对学生的学法起着‘点拨与‘引路”的作用，它能为学生创设在实践操作中充分发挥聪明才智的理想情境，它能以实践指导学法，调控学法的优化组合。但教学中不规范的操作会留下诸多问题，会给学生造成“错觉”，有碍于学生新知的形成，甚至会把学生引向“歧途”。因此，教师在教学中操作演示的规范与否，会直接影响到学生的学法习得，影响其概念、法则的形成。下面结合实践经验谈谈教师操作演示规范化的重要性。

一、注意操作的细致性，忌走过场

操作的细致性是指教师操作不能走过场，每一个细节都要到位，让学生的思路能跟上教师的节奏，否则学生动手操作时思维过程就会出现紊乱，对新知的形成会造成很大的障碍。

在学习“圆锥的体积”时，我听过两位老师上的课，第一位老师直接用等底等高的圆柱、圆锥倒水做演示实验，让学生观察后，得出V锥=1/3V柱。学生能记住，亦能解决一些问题，但不知其来龙去脉，很难进行知识的整合与灵活运用。第二位老师将全班同学每8人分成一组，每组准备四盆黄沙、四个圆柱、四个圆锥（等底不等高、等高不等底、等底等高、底高都不等），小组活动前进行了细致地操作指导议一议实验怎么做？工具怎么选，选择怎样的圆柱、圆锥实验？在学生自主分工合作，完成实验后，指导思考：为什么选等底等高的圆柱和圆锥进行实验？你能发现它们的体积之间有怎样的关系？在这样的小组活动中，人人参与操作体验，认真全面分析现象，主动表达自己的一些直接感受，相互合作交流，达成共识，引出规律：V锥=1/3V柱。这样的安排由于学生有了动手实践、主动探究、合作交流的亲身经历，得到的知识是充分内化的，是深刻的，容易理解，而且能举一反三，较好地解决实际问题。

二、注意操作的完整性，忌省略式

教师的操作直接影响到学生操作习惯的形成。例如一位老师在教学分数连乘时，在对连乘综合算式进行计算约分时，这样进行过程操作呈现：

由于教师省略了约分后的“1”，显然对计算结果是没有影响的，但对一些学困生来说，他们的思维能力、反应速度往往滞后与其他同学，不能与教师同步，以至于有的学生在今后的练习中会出现以下的问题：

这里，学生由于教师缺乏完整性的操作而形成了错误的表象，自以为后部分互相约分后就不存在了I结果把后半部分约分以后的结果当成了0。如果教师注意到操作的完整性，就完全能够避免这种情形的发生，同时教师注意操作完整性，同时也给学生树立榜样，有利于培养学生一丝不苟的学习习惯，提高练习的正确率。

三、注意操作的有序性，忌隨意性

教师操作的有序能体现学生认知的思维过程。操作的随意性会给学生造成认知的“错觉”。如画一个平角，有的教师先画一条直线，然后在线上点一个点，致使学生误认为平角就是一条直线。我们知道，构成角的要素有：一个顶点和从这个顶点引出的两条射线。如果教师注意了操作的有序性，先确定角的顶点，然后以角的顶点为端点，分别向相反方向画两条射线，就能避免出现认知错误。

四、注意操作的多角度性，忌单一性

这里的多角度性是指教师在操作演示让学生体会事物的本质特征时，要将操作对象置于不同的位置、角度，有目的、有计划地变更操作对象的非本质特征，而使本质特征不变。通过这样的观察、比较，有利于学生形成清晰的表象，有效克服思维定势的影响。

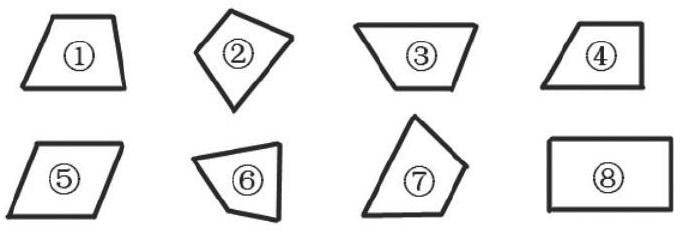
例如，一位教师在教学梯形的认识时，先给学生呈现的大多都是“标准位置”的图形，让学生把握梯形的特征。在而后巩固练习中，教师出现了不同位置放置的四边形，让学生判断哪些是梯形，哪些不是梯形。（如图）

结果图①③④学生容易辨认；图②⑦辨认困难；图⑥辨认错误。如果教师在呈现给学生看“标准位置”的梯形时，能将其中一两个的位置进行变换，让学生的思路拓宽后，再将形状、位置、大小不同的梯形放在一起让学生分辨，这样有助于学生分清图形的本质特征和非本质特征。

总之，教师规范地操作演示在数学教学中具有重要的作用。作为教师，我们应根据小学生的思维发展特点和认知规律，根据教学内容积极创造条件，在教学中细致地、完整地、有序地、多角度地进行规范操作演示，加强动作和思维的联系，引导学生参与知识的形成过程，体验成功的喜悦，从而达到培养兴趣，发展思维，提高教学质量的目的。