例谈多面体三视图的还原策略

广东省东莞中学(523005) 于涛

在高中数学的教学里,我们有两种用平面图形表示立体图形的方法—直观图和三视图.其中,三视图可明确表达立体图形的长度、高度和宽度.但是,要想反映几何体的空间结构与关系,我们则需要根据三视图推演出立体图形的直观图,同时,三视图的还原问题亦是培养学生空间想象力和逻辑思维能力的有效手段,所以,它也是高考数学的重点考查内容之一.高三复习中,学生对多面体相关的三视图还原问题较为惧怕.仅仅依靠空间想象力,很难快速并准确地解决三视图还原问题.因此,本文试图提供一种多面体三视图还原的有效方法和策略.

1.高考真题,情境再现

题目 (2014年高考全国新课标I卷理科第12题)如图1,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )

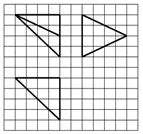
图1

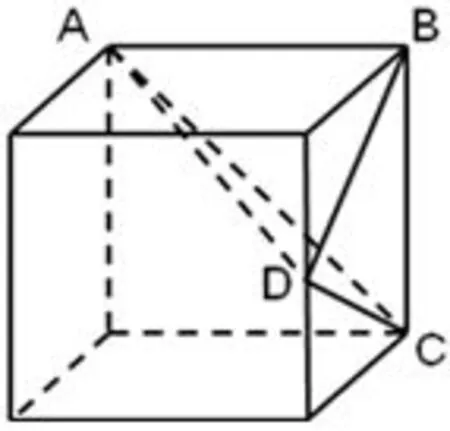
图2

这个题目的几何体是三棱锥,但是从摆放位置来看,只有一个顶点落在“底面”支撑图形.从构题角度来讲,是将原有多面体进行了巧妙地翻转,正是这一翻转增大了三视图还原的难度.

学生在完成该三视图还原时,不仅耗时长,而且准确率低.面对不是三棱锥的多面体翻转之后形成的三视图还原问题,更是难上加难,这不得不让我们要好好的思考该如何推动学生思维的发展,突破三视图还原的难点.

2.策略提炼,多维实践

2.1 三视图还原策略的整体结构

三视图是立体图形在不同方向上的投影,投影过程中遵循的对应关系均是点、线、面间的对应关系,立体图形中的每一个面并不一定真实可见.考虑到几何体的形成要素是点、线、面,类比于立体几何公理2(过不在一条直线上的三点,有且只有一个平面)及其推论确定平面的方式,要想迅速解决三视图的问题,我们把确定几何体的过程分为三大环节:

(1)通过定性分析,明确几何体落入的载体;

(2)通过定量分析,明确形成几何体的几何要素(点、线、面);

(3)成图检验.

根据三视图对几何体进行定性和定量分析的实施过程如下:通过三视图对几何体进行定性分析,判断几何体是不是锥体;若是锥体,则对锥体进行点(顶点)、面(底面)的定量分析;若不是锥体,则再次对几何体进行定性分析,明确几何体落入的最小载体或载体(载体一般以长方体、棱柱较为多见),针对最小载体,则通过在载体表面画线(棱)的方式进行定量分析;针对一般载体,则通过删除不需要的点或增加需要的点的方式进行定量分析.该实施过程体现了三视图还原的逻辑结构,如下图3所示:

图3

上述三视图还原策略的逻辑结构中,共有3种解题方法,不同方法的定量分析遵循了3种几何要素确定几何体的原则:(1)锥体可以由顶点(点)和底面(面)确定;(2)多面体可以由外表面的棱(线)确定;(3)多面体可以由各顶点(点)确定.

2.2 三视图还原策略的三种实施方法

2014年高考全国新课标I卷理科数学第12题的三视图还原问题具有典型性,解题策略中的三种方法均可解决该问题,具体过程如下.

方法1由几何要素点(顶点)、面(底面)确定锥体

定性分析:①判断几何体是不是锥体(方法1的判断结果为“是锥体”);

定量分析:②明确顶点位置及相应底面位置;

成图检验:③连接顶点与底面各顶点成图,④检验.

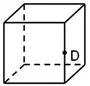
图4-1

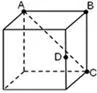
图4-2

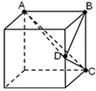
图4-3

具体实施步骤:

(1)如图1,根据俯视图和侧视图明确该几何体是锥体,明确顶点D的位置,如图4-1所示;

(2)根据正视图及侧视图明确与顶点D相对应的底面ABC的位置,如图4-2所示;

(3)分别连接 DA、DB、DC,明确几何体为锥体D-ABC,如图4-3所示;

(4)检验几何体D-ABC的三视图与题目相符.

该方法主要应用于锥体的还原,非锥体应用该方法较为困难,有一定的局限性.方法1的实施还可以由正视图和俯视图确定顶点,侧视图确定底面形成几何体.

方法2由几何要素线(棱)确定多面体

定性分析:①判断几何体是不是锥体(方法2的判断结果为“不明确是锥体”);②根据三视图中较简单的视图确定几何体落入的最小载体;

定量分析:③根据正视图前实后虚,俯视图上实下虚,侧视图左实右虚的原则在载体的前、后、上、下、左、右依次划线(线条将会自动连成封闭图形,将载体切割成几部分);

成图检验:④明确几何体并检验.

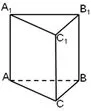
图5-1

图5-2

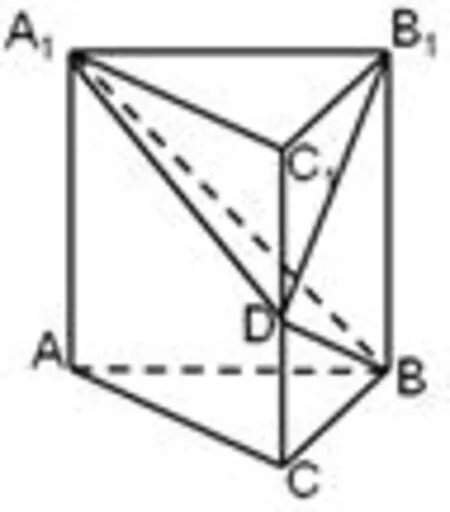
图5-3

具体实施步骤:

(1)如图1,不明确是锥体;

(2)俯视图和侧视图都较为简单,均可将几何体放入相应三棱柱,根据视角,选择拉伸俯视图,明确几何体落入的最小载体是三棱柱ABC-A1B1C1,如图5-1所示;

(3)根据正视图中的两条斜线,配合侧视图,在载体前面画线A1D、后面画线A1B,如图5-2所示;

(4)根据侧视图,配合正视图,载体左面线条与A1D重合,在右面画线B1D、BD,如图5-3所示;

(5)载体恰好被连成的封闭图形分成了三个部分,根据三视图明确几何体为中间部分的锥体D-ABC(包含检验).

方法2的实施体现了由线(棱)形成几何体的过程,实施过程中三个视图依次画线,通过用俯视图明确最小载体,用正视图和侧视图在载体上画线,进而切割载体,实现了几何体的还原.方法2还可以用侧视图确定最小载体(若用该三棱柱做最小载体,不妨用正方体衬托该三棱柱),用正视图和俯视图画线切割载体.

方法3由几何要素点(顶点)确定多面体

定性分析:①判断几何体是不是锥体(方法3的判断结果为“不明确是锥体”);②根据三视图中较简单的视图确定几何体落入的载体(可以是最小载体,也可不是);

定量分析:③依次根据正、俯、侧视图删除载体中不需要的点或增加一些需要的点;

成图检验:④连线成图并检验.

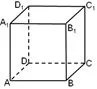
图6-1

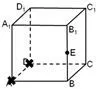
图6-2

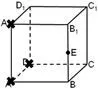
图6-3

图6-4

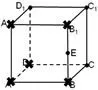
图6-5

图6-6

具体实施步骤:

(1)如图1,不明确是锥体;

(2)确定正方体ABCD-A1B1C1D1为载体,如图6-1所示;

(3)根据正视图,删除点A、D;配合俯视图和侧视图增加点E,如图6-2所示;

(4)根据俯视图,删除点A1,如图6-3所示;

(5)根据侧视图,删除点B、B1,如图6-4所示;

(6)根据前5步,明确载体上剩余的点为E、C、C1、D1,如图6-5所示;

(7)连线成图并检验,明确几何体为棱锥E-CC1D1,如图6-6所示.

方法3的实施也可以与方法2的定性分析一致,明确几何体落入的最小载体,在最小载体上进行删除点或增加点.

三种方法的应用范围与方式不同.方法1仅对锥体的还原有优势,适用范围有局限性;方法2的应用对载体要求较高,需要明确最小载体,对切割形成的几何体尤为适用;方法3的应用对载体要求不高,具备较高的普适性,当视图线条较多,不容易明确需要删除的点和增加的点时,可选择方法2.三种解题方法的有机结合形成了三视图还原一般解题策略的逻辑结构,反映了多面体三视图还原过程中思维自动化的路径,便于找到不同三视图还原题目的最优解决方式.

3.举一反三,触类旁通

三视图考查方式主要以选择填空为主,设问多为还原几何体后求体积、表面积、最大面面积、最长棱长等.不论哪种设问方式,还原几何体是核心,因此所选三个例题设问均为求体积.除了能应用三视图还原的策略,还能体现该策略中“载体”的优越性,利用载体求体积正是求体积常见方法“割形补形”中的补形.

例1已知某几何体的三视图如图7所示,则该几何体的体积为( )

A.2 B.4 C.6 D.12

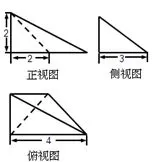
图7

图8

例2已知某几何体的三视图如图8所示,则该几何体的体积为( )

例3已知某几何体的三视图如图9所示,则该几何体的体积为( )

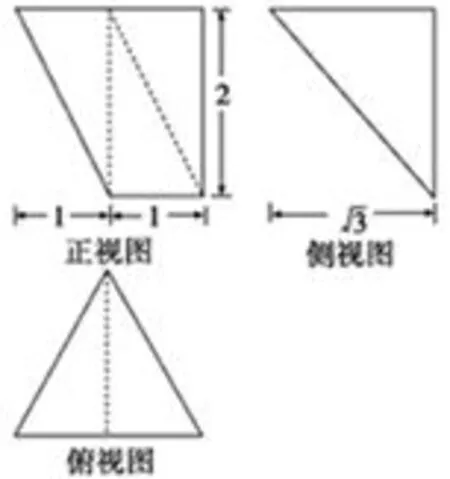
图9

观察三个例题的三视图,通过定性分析可判断例1中的几何体为锥体,应用策略中的方法1;例2、例3的几何体不明确,考虑方法2或3;根据图8三个视图都有正方形且线条较多,应用策略中的方法2;根据图9三个视图的形状,通过不同视角较容易删除不需要的点,应用策略中的方法3.

4.举重若轻,返璞归真

学生在通过学习立体几何培养空间想象能力的过程中,最先接触到的是正方体,然后便是棱柱.在应对三视图还原问题时,为了化解思维难点,以学生最为熟悉的几何体(正方体、棱柱)为载体,再进行几何要素的定量分析.这样的方式符合学生思维发展的规律,大大减少了分析三视图还原问题的思维量,提高了解题效率.无论是知识教学还是解题教学,我们需要关注学生思维发展的最近发展区,从已有知识,从最熟悉的知识出发,定能更好地帮助学生突破难点,推动学生思维的发展,实乃举重若轻,返璞归真！