基于D-S证据理论的CT/ECT图像融合实验方法

司志宁，田 沛，张立峰

（华北电力大学自动化系，河北 保定 071003）

0 引 言

现代工业监测过程中存在大量两相或多相流分布的问题，如电厂输煤管道中煤、气分布直接影响煤粉燃烧效率，石油勘探中天然气、原油和水的比例分配将直接影响开采效率。精确检测各相分布对于工业过程优化与控制有着重要意义；因此，过程层析成像技术（process tomography，PT）近些年来迅速发展起来，该技术采用非侵入的外置传感器阵列方式，在线获取封闭管道内某截面的各相分布状况[1-2]。

然而，PT技术的成像机理决定了单一模态技术的局限性，如射线层析成像技术（computed tomography，CT），其具有硬场特性，重建图像分辨率较高，但有限的几个固定角度获取的投影数据，使得重建图像趋于多边形，与实际流型分布不相符[3]；电容层析成像技术（electrical capacitance tomography，ECT）具有软场特性，使得重建图像精度较低，但其电容极板的配置和测量方式使重建图像能够较真实地反映被测流型的形状[4]。同时，欠定方程组的病态问题，以及工业过程实时监测的要求，对PT技术的硬件和图像重建算法均提出很高的要求。因此，将CT、ECT成像技术双模融合，可在短时间内以较小的代价获取单一模态无法获取的更精确的流型特征[5]。

基于D-S证据理论在不确定性、模糊性方面的优势，本文提出将D-S证据理论应用于CT/ECT图像融合，将同一流型的CT、ECT重建图像像素聚类后，运用D-S合成规则进行融合。

1 D-S证据理论

1.1 基本原理

D-S证据理论摒弃了贝叶斯理论中的统一识别框架、先验概率以及条件概率等硬性要求，通过识别框架、基本概率赋值函数、信度函数等概念对不确定性进行描述，显示了其在不确定性、模糊性方面的优势[6]。

证据理论的基础是证据的合成和信度函数的更新。识别框架Θ，是关于命题的互斥、可穷举的有限集合，幂集2Θ表示所有可能的命题集，即包含了Θ的所有子集。证据理论的基本概率分配由基本概率赋值函数（basic probability assignment function，BPAF）表示，其定义[7]如下：

定义1：识别框架Θ上的集函数m：2Θ→[0，1]满足：

1）空集（空命题）不产生任何概率，即：

2）Θ中全部命题的基本概率分配总和为1，即：

则称m为识别框架Θ上的基本概率赋值函数BPAF，也称为基本可信度分配函数或mass函数，反映了命题在某证据条件下所有可能事件的概率大小。

定义 2：设Θ为识别框架，m：2Θ→[0，1]为Θ上的基本概率赋值函数，则称由：

所定义的函数 Bel：2Θ→[0，1]为Θ上的信度函数（belief function）。

1.2 D-S合成规则

D-S合成规则是一个反映多证据之间联合作用的法则。两个或多个相互独立的置信函数可以用D-S合成规则来组合，通过计算基于不同证据来源置信度的正交得到一个新的置信函数[8]。

定义3：设Bel1和Bel2是同一识别框架Θ上的两个信度函数，其相应的基本概率赋值函数为m1和m2，焦元分别为Ai和Bj，则 D-S 合成规则[9]为

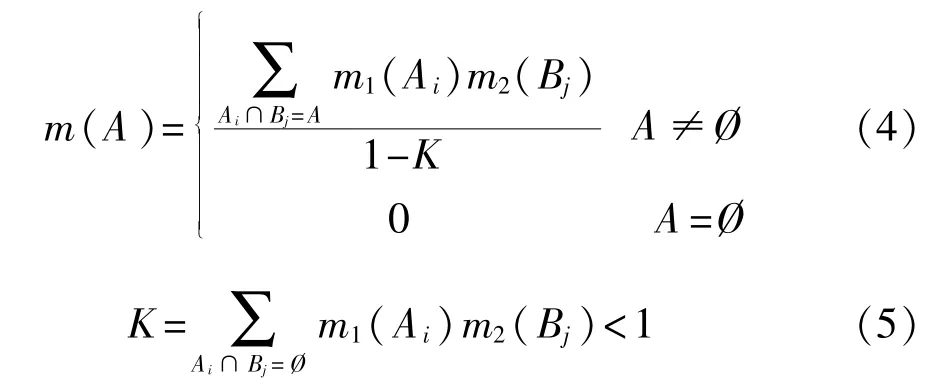
式中K反映了各个证据之间的冲突程度，系数1/（1-K）称为正则化因子。由m给定的基本概率赋值函数称为m1和m2的正交和，记为m1⊕m2。若K=1，则称m1和m2的正交和m1⊕m2不存在，不能对基本概率赋值函数合成。

2 CT/ECT图像融合

2.1 基本概率赋值的获取

D-S证据理论中合理构造基本概率赋值函数是一个与应用密切相关的问题，也是实际应用中的关键和难点，直接影响着最终融合结果的准确性和合理性[10]。

在工业油/气两相流中，理想流型的图像常为0和1的二值图像，而过程层析成像系统重建的图像为[0，1]的灰度图像。对于解决图像中像素层面的信息如何合理转化为待融合的数据信息问题，受模糊c-均值聚类算法（fuzzy c-means algorithm，FCM）[11]的启发，本文将[0，1]的灰度图像划分为油相和气相两大类，进一步说，该问题在像素层面的证据理论的命题有两个：1）代表气相的灰度值为0的像素点及其周边邻域；2）代表油相的灰度值为1的像素点及其周边邻域。这是两个完全不相容的命题，正符合D-S证据理论的要求。

进一步，需要将图像表达形式的信息转化为证据，即重建图像中，每个像素所包含的灰度信息，应当转换为对上述证据命题的置信度，即证据理论中的基本概率赋值函数。模糊聚类算法中的隶属度矩阵代表的是每个像素针对各个类别的归属情况，且单个像素在各个类中的所有隶属度之和等于1，而这正好和证据理论各个命题的置信度的意义相符，因此可以将隶属度矩阵中的元素看作是证据理论中对应命题成立的基本概率。隶属度函数[12]如下：

式中：c——类别数，c≥2；

n——像素个数；

dik——聚类中心νi与第k个像素值xk之间的欧几里德距离（Euclidean distance）；

μik——像素值xk在第i类中的隶属度，且μik是介于0，1之间的值。

由前所述，本文设定c=2，ν1=0，ν2=1。

2.2 融合过程

CT图像与ECT图像的融合过程可转化为D-S证据理论融合过程。针对同一流型，设CT和ECT重建图像像素分别是同一识别框架Θ上的两个信度函数，其相应的基本概率赋值函数为m1和m2，m则表示融合图像像素的基本概率赋值函数，焦元分别为气相A1和油相A2，且运用隶属度函数μik表示基本概率赋值函数，如表1所示。

表1 基本概率赋值函数表

由聚类中心ν1=0，ν2=1，根据隶属度函数μik可推得融合图像像素值xk：

即：

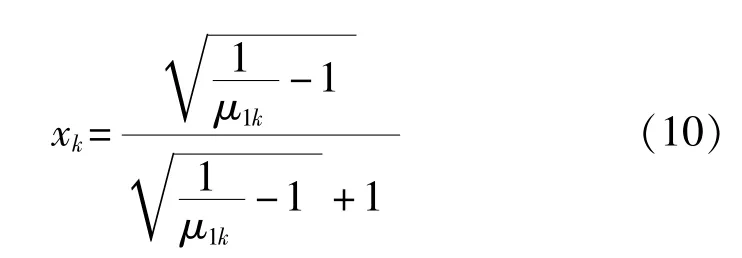
据此，完成像素-概率-像素之间的转化，即：将CT、ECT待融合图像的像素值聚类化，运用隶属度表示其基本概率分配，运用D-S证据理论融合得融合图像概率分配，即融合图像像素值隶属度，进而推得融合图像像素值，重构融合图像。CT/ECT图像融合流程图如图1所示。

3 实验及结果

图1 CT/ECT图像融合流程图

分别对3种油/气两相流流型进行图像融合实验，仿真流型如图2所示。被测管道直径为82mm。CT系统采用5源17探测器结构，通过静态实验装置测得射线投影数据；ECT系统采用16电容极板传感器阵列结构，运用COMSOL仿真软件获得电容投影数据[13]。考虑到系统实时性要求以及D-S证据理论融合效果，本文均采用线性反投影算法（linear backprojection algorithm，LBP）重建图像。LBP算法在图像重建过程中无需求解大型矩阵的逆，计算量较少，使得图像重建速度快，但其将投影域按照均匀介质分布划定，不考虑软场效应，所以导致重建图像精度较低[14]。

图2 仿真流型

为了验证D-S证据理论在CT/ECT图像融合中的有效性，分别运用平均值法、小波变换法和D-S证据理论对上述两种模态的重建图像进行融合对比；其中，小波变换采用Daubechies小波基db4进行分解，分解层数均为3层，低频系数采用平均值法融合，高频系数采用绝对值选大法融合。重建图像与融合图像对比如图3所示，图像像素灰度值均归一化至[0，1]范围内。

从图中可看出，对于CT系统，5源17探测器的结构，使得重建图像边缘呈五边形，但射线的硬场特性（射线具有直线穿透能力且不因介质分布而改变传播方向）决定了图像分辨率较高；而ECT系统，由于敏感场的软场特性（即敏感场分布受被测介质分布的影响），使得图像分辨率较低，但16电容极板的对称配置使重建图像较真实地反映仿真流型的形状；线性反投影算法重建图像质量均不高，伪影现象严重。从视觉效果上而言，3种流型融合图像对比单模态重建图像的精度均有所提高，融合图像既改善了CT图像边缘失真的缺点，也避免了ECT软场特性的干扰。

对比3种融合方法的视觉效果可以看出，基于平均值和小波变换的融合方法，由于未考虑CT、ECT图像特点以及融合目的，仅从图像本身出发，使得其在核心流和环流中对图像质量的改善并不明显，且融合图像依然存在较大伪影，未达到预期融合目的。而本文采用的基于D-S证据理论的融合方法，充分利用了CT、ECT图像的先验信息，在3种流型中融合图像均更加接近原型，提高了过程层析成像重建灰度图像的0、1信息度，融合效果最佳。同时，基于小波变换的多分辨分析方法会对系统实时性产生较大干扰，而D-S证据理论基于统计学方法，未进行复杂的频域多尺度分解，降低了对系统实时性要求的干扰。

对融合前后的图像质量评价采用均方根误差指标（root mean square error，RMSE）[15]，即：

式中：Ii（i，j）——仿真原图坐标（i，j）点像素值；

If（i，j）——融合图像对应点（i，j）点像素值；图像的大小为M×N。

RMSE越小，说明融合图像与理想图像越接近，也就是说融合效果越好。

评价结果如表2所示，平均值法与小波变换法的融合图像在层流型中误差大于CT图像，在核心流和环流型中稍有减小，而本文采用的D-S证据理论的融合图像在3种流型中的误差均明显降低，提高重建图像的准确度和信息量，客观地验证了D-S证据理论在CT/ECT图像融合中的有效性。

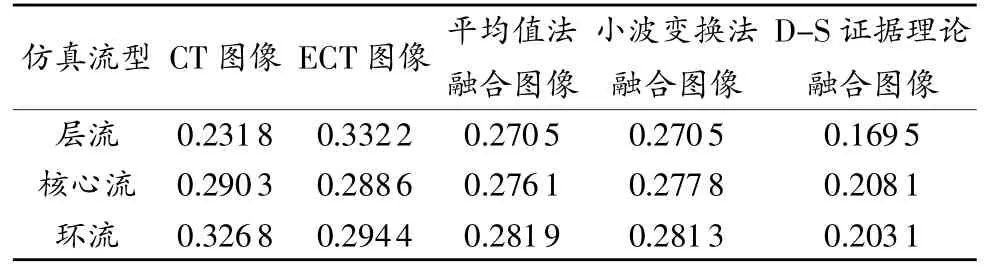
表2 图像均方根误差的比较

4 结束语

图3 重建图像与融合图像对比

本文基于D-S证据理论，运用聚类算法中的隶属度函数表示证据理论中的基本概率赋值函数，对CT、ECT重建图像进行融合，实现像素-概率-像素之间的转化。在提高单模态成像质量的同时，同其他传统像素融合算法对比，实验结果表明融合图像更加接近原流型，客观评价误差显著减小，同时对系统实时性干扰较小，验证了D-S证据理论在CT、ECT双模态融合中的有效性。

[1]谭超，董峰.多相流过程参数检测技术综述[J].自动化学报，2013，39（11）：1923-1932.

[2]马平，周晓宁，田沛.过程层析成像技术的发展及应用[J].化工自动化及仪表，2009，36（1）：1-5.

[3]薛倩.多相流CT系统成像算法研究及软件设计[D].天津：天津大学，2010.

[4]赵玉磊，郭宝龙，闫允一.电容层析成像技术的研究进展与分析[J].仪器仪表学报，2012，33（8）：1909-1920.

[5]谭超，许燕斌，董峰.多模态流动成像技术研究进展[J].仪器仪表学报，2015，36（2）：241-253.

[6]DEMPSTER A P.Upper and lower probabilities induced by A multiplicand mapping[J].Annals of Mathematical Statistics，1967（38）：325-339.

[7]SHAFER G，LOGAN R.Implementing dempster's rule for hierarchical evidence[J].Artificial Intelligence，1987（33）：271-298.

[8]谬燕子，方健，马小平，等.D-S证据理论融合技术及其应用[M].北京：电子工业出版社，2013：8-24.

[9]杨风暴，王肖霞.D-S证据理论的冲突证据合成方法[M].北京：国防工业出版，2010：15-40.

[10]王秀秀.基于证据理论的图像融合新算法及应用[D].天津：天津大学，2008.

[11]陈晓霞.基于FCM图像融合技术的研究[D].武汉：湖北工业大学，2013.

[12]RUSPINI E H.A new approach to clustering[J].Information&Control，1969，15（1）：22-32.

[13]李佳，张立峰，田沛.基于Kalman滤波的ECT图像重建算法[J].传感器与微系统，2015，34（8）：128-130.

[14]张立峰.电学层析成像激励测量模式及图像重建算法研究[D].天津：天津大学，2011.

[15]高超.图像融合评价方法的研究[J].电子测试，2011（7）：30-33.