基于加权最小二乘法的弹体转速测量方法研究

李文豪，秦 丽，刘一鸣，杨文卿

（中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051）

0 引 言

某型旋转弹，其弹体运动于高过载高旋的复杂环境下，弹体转速测量难度大进而影响了弹体的姿态准确解算，最终严重影响了炮弹的打击精度。为实现精确打击，研究弹道信息等原因，需要实时测量高旋弹药的运动状态。

微机电系统（micro-electro-mechanical system，MEMS）传感器具有体积小、质量轻、功耗低、成本低、可靠性高等优点，同时旋转弹内空间有限，所以目前弹体转速测量系统大多采用MEMS器件[1]。但是，由于大量程的MEMS惯性器件往往测量精度不高，且容易受振动、噪声等因素的影响，因此弹体转速的测量精确严重制约了弹体的姿态测量、解算以及制导。目前，国内各个领域在多传感器数据融合方面已经进行了大量的研究，并且取得了一定的成就[2-5]。本文在不改变测量所使用的传感器的前提下，通过加权最小二乘法算法将多个传感器所获取的数据进行融合处理从而得到更加精确的弹体的转速[6-7]。

1 弹体转速测量基本原理

弹体发射后轴向滚转角速率短时间内急剧增大，最高可达20r/s，但是其余两轴上的角速率却相对较小，大量程MEMS陀螺仪虽然能敏感到弹体转速，但由于精度低以及噪声、振动等原因，通常会给弹体转速测量结果造成较大的误差，以这样的数据进行弹体的姿态解算，必然带来极大的偏差[8]。

为解决弹体转速难测量这一问题，构造如图1所示的系统。光电编码器转动轴与外筒固联，出线端与内筒固联。当外筒高速旋转时，转动轴跟随外筒旋转，编码器机身跟随内筒旋转，因此可以输出内筒与外筒的相对转角。并且由于编码器自身特性，其输出角度信号的误差不随时间累积，完全由编码器本身的分辨率决定，所以只需对该相对转角进行微分，便能得到内外筒相对角速率。

图1 弹体转速测量系统结构图

外筒轴线上固联一个大量程陀螺仪G1（7200°/s）以测量外筒转速。伺服电机机身与外筒固联，转动轴与内筒以联轴器连接。电机以模拟电压形式控制，并以外筒大量程陀螺仪输出为控制信号进行反转，同时带动内筒旋转，形成一个隔转止旋的稳定平台。理论上可使内筒滚转角速率为零，但由于种种原因造成的误差，内筒依然会以较小的角速率转动，但这时内筒角速率已可以稳定在较小范围，所以内筒MIMU（微惯性测量单元）在X轴上可以采用量程为400°/s的陀螺仪G2；同时，MIMU之外，内筒X轴上还存在一个量程为900°/s的陀螺仪G3，以防止电机减旋效果不佳，内筒转速超量程。

为了获取弹体飞行过程中的转速信息，首先需要分析弹体在不同转速下，滚转轴向上的各个陀螺仪的工作状况。当弹体点火发射后极短的一段时间内速率变化极大，因为伺服电机的控制存在延迟，电机输出转矩不可能瞬间增大到带动内筒相对地面静止的状态，所以减旋效果不佳。此时内筒转速可达700°/s，内筒MIMU中的陀螺仪G2已经处于饱和状态，内筒大量程陀螺仪G3能正常工作。一段时间后电机转矩输出稳定，能有效带动内筒反旋，达到减小内筒滚转角速率的作用。此时内筒角速率一般小于100°/s。设定外筒大量程陀螺仪G1测出的转速为ω1，光电编码器测得的相对转速ω2；内筒MIMU中的陀螺仪G2输出为ω3；陀螺仪G3输出为ω4。当滚转轴线上的3个陀螺仪与光电编码器P均可正常工作，存在表达式

即外筒转速等于内筒转速与光编转速之和。因为系统中存在多个传感器对同一物理量的测量，所以为了精确复现外筒转速，并充分利用多个传感器的数据，本文通过加权最小二乘法进行数据融合，来计算外筒转速的无偏估计。

2 加权最小二乘法分析

因为外部干扰及器件精度等原因，单个传感器的测量存在一定的不确定性和局限性，其输出误差对系统的性能影响极大[9]。为了解决单个传感器测量的以上缺陷，本文利用加权最小二乘法进行多传感器数据融合，增强了系统数据的可靠性。不直接使用最小二乘法是因为各个传感器噪声不一致，可信度不同，如果不分优劣的使用这些传感器的测量值，那么精度提升并不高，所以采用加权的方法分别对待各个量进行测量[10-12]。

多个传感器对同一物理量测量时，记传感器的测量值为Z，被估计量为X，一般是无法直接测量的值，Z是X的各分量的线性组合，其随机测量噪声为V，则存在：

其中H为测量值与估计值的转换矩阵，加权最小二乘法求取准则为

式中W为正定对称加权矩阵，W的取值关乎估计量的精度。为使式（3）成立，变形可得，加权最小二乘估计量方程：

本文所述的传感器测量噪声矩阵可以认为是均值为0，方差为固定值R的白噪声，则加权最小二乘估计是无偏估计。正定对称加权矩阵W与均方误差矩阵存在

认为每个传感器之间相互独立，则噪声方差阵中非对角线上的元素为0，即协方差为0。此时噪声方差阵为对角矩阵，容易得知：

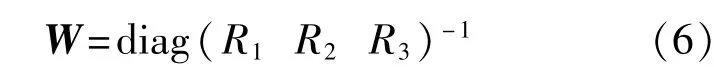
其中R1为大量程陀螺仪G1方差，通过下式求得

通过式（1）可知，内筒陀螺仪与光电编码器输出微分之和才能表示外筒转速。说明内筒两个陀螺仪的方差均不能直接参与计算，需要进一步分析。显然内筒陀螺仪输出与光电编码器输出是不相关的，所以存在：

测量值与估计值之间的转换矩阵显然为3×3的矩阵，但因为各传感器之间互不相关，且传感器输出为电压值，所以可使用下式表示：

其中Ki为第i个传感器的标度因数，单位（V/g），表征电压值与转速之间的比例系数。

设3个精度从高至低陀螺仪的测量量分别是Z1，Z2，Z3，测量误差是均值为 0，方差分别为r1，r2，r3，所以有：

马尔科夫估计的均方误差为

式（13）说明，理论上，使用加权最小二乘估计的效果比单独应用精度最高的传感器测量效果更好。

3 试验验证

为验证加权最小二乘法计算弹体转速的有效性，需要进行相应的实验。本文将通过车床实验所得的数据进行分析对比。车床实验是指将测试设备水平装载至高速精密车床上，如图2所示，并驱动车床以不同转速旋转，来模拟弹体滚转轴高速旋转时的飞行环境，但为了数据便于处理，俯仰和偏航一般保持不变。通过加权最小二乘法计算外筒转速并与车床实际转速进行对比，以算法计算结果与实际值之间的误差大小作为评判算法优劣的指标。

图2 车床实验

3.1 实验数据预处理

本文进行车床试验时，选取220，450，700，870 r/min 4个转速对测试系统进行旋转，且每个转速持续旋转并达到平稳的时间≥30s，系统采样率为5000Hz。最后将采集得到的数据通过软件Matlab进行分析计算。

需要注意的是，车床受自身精度、老化及负载质量等因素的影响，并不能保证完全精确的在上述4个转速上旋转。本文在外筒俯仰轴上添加一个加速度计，并利用其输出特性来精确测量车床转速。在平稳旋转过程中，旋转过程中加速度计轴向上敏感到的重力分量以正弦形式变化，因此正弦信号的频率即为转速。图3、图4分别为俯仰轴上加速度计在220r/min和700r/min转速下的输出信号。

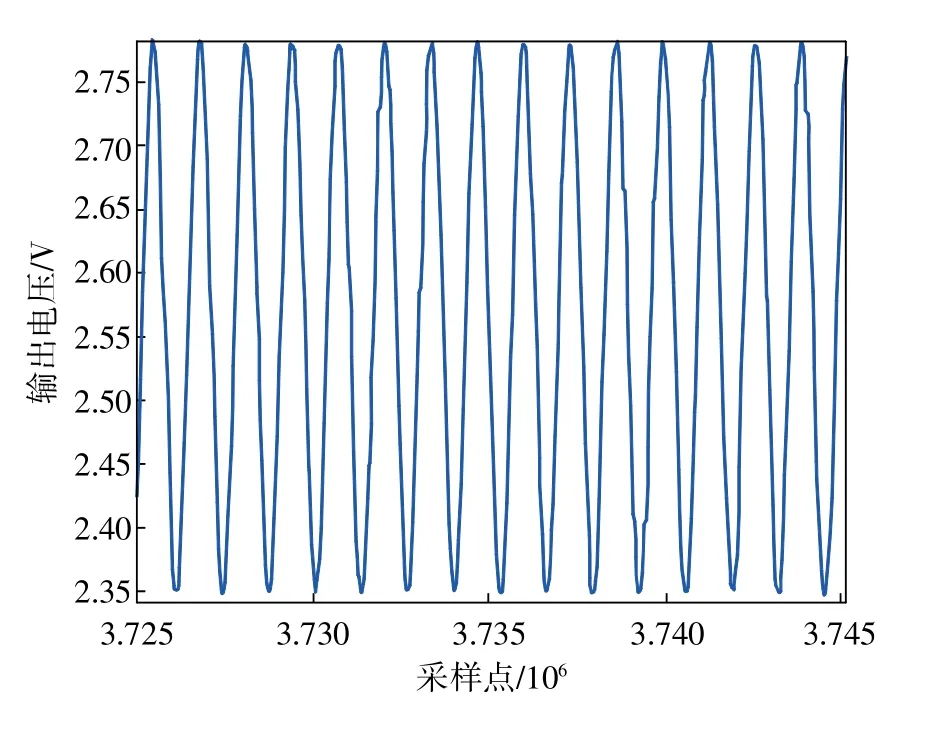
图3 220r/min时加速度计输出

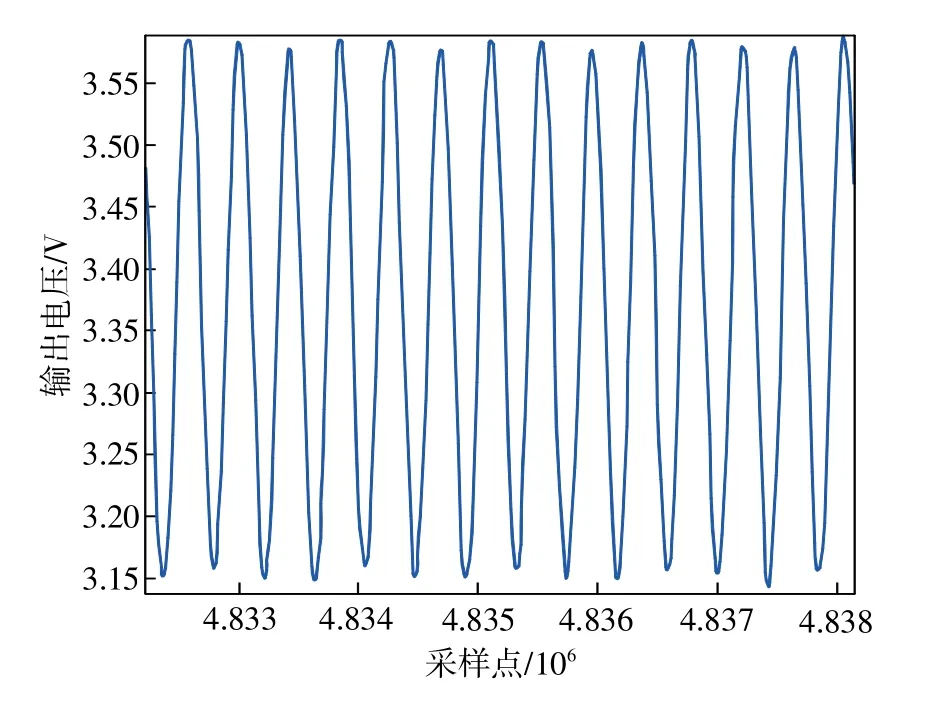
图4 700r/min时加速度计输出

3.2 融合算法有效性验证

3个陀螺仪零点输出截取数据如图5～图7所示。

图5 陀螺仪G1零位输出

表1 各陀螺仪方差与权重系数

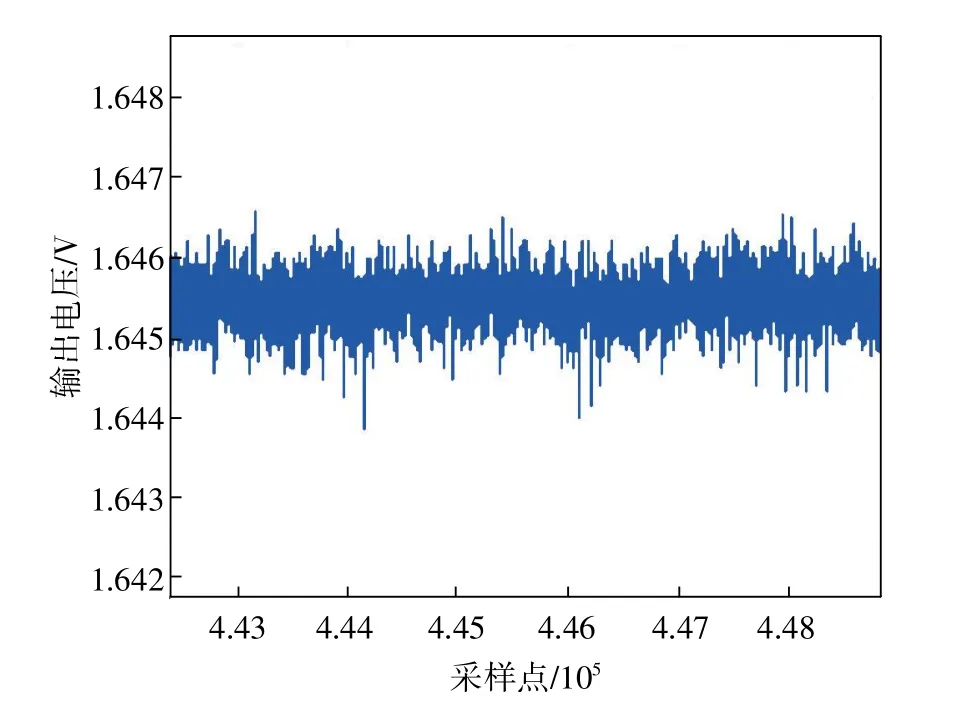
图6 陀螺仪G2零位输出

图7 陀螺仪G3零位输出

根据以上数据和式（12）求出的3个陀螺仪方差以及权重系数如表1所示。

按3.1进行车床实验，陀螺仪G1输出如图8所示。由于光电编码器输出为角度且为单圈输出模式，所以为了得到其所测量的转速，需要对原始数据进行相应处理，图9为经过拉伸并微分后得到的光电编码器输出数据。图10、图11分别为陀螺仪G2、G3输出数据。

图8 陀螺仪G1输出

图9 光电编码器P输出

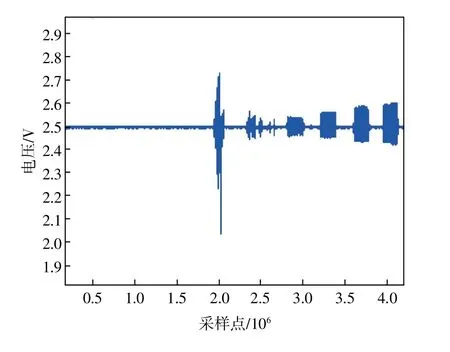
图10 陀螺仪G2输出

图11 陀螺仪G3输出

表2 各种方法所测转速对比表

进行数据融合后与3个不同量程的陀螺仪分别计算得到的转速进行对比，结果如表2所示。

从表中可以看出，单一的使用陀螺仪G1测量弹体转速，误差较大；用内筒加光电编码器的方法所测得的弹体速率虽然精度有一定提高，但是远达不到1°/s的要求；多个传感器融合后的计算结果比单独使用最高精度陀螺仪G2所求得的结果的精度要高的多，测量精度提高了一个数量级，与理论相符。

4 结束语

弹体转速的精确测量是高旋弹药实现导航制导的关键之一，由于受目前传感器测量精度的限制，很难通过大量程MEMS陀螺仪直接测量。为此设计了隔转止旋的稳定平台，并通过加权最小二乘法，将多个传感器的数据进行融合，充分利用了装置中的不同量程的陀螺仪测量数据，求得了更为准确的弹体的滚转角速率信息，最终测量精度提高了一个数量级。通过车床实验对该方法的有效性进行了验证，试验结果表明该方法可以广泛应用于各种转速测量装置，且具有一定的工程应用价值。

[1]刘俊，石云波，李杰.微惯性技术[M].北京：电子工业出版社，2005.

[2]张品，董为浩，高大冬.一种优化的贝叶斯估计多传感器数据融合方法[J].传感技术学报，2014（5）：643-648.

[3]刘永广.基于多传感器数据融合的输电杆塔健康状况监测系统设计与实现[D].太原：太原理工大学，2016.

[4]廖武.体域网中多传感器数据融合算法的研究[D].长春：吉林大学，2016.

[5]黄朝，许鑫，刘敦歌，等.基于多传感器的微弱磁异常信号提取方法研究[J].电子测量技术，2015，38（10）：91-95

[6]李杰，赵诣，刘俊，等.高旋弹药飞行姿态测量用半捷联MEMS 惯性测量装置研究 [J].兵工学报，2013，34（11）：1399-1403.

[7]LI J，LIU J，ZHANG W D.MEMS based micro inertial measurement system[J].Wseas Transactions on Circuits and Systems，2006（5）：691-696.

[8]李杰，洪惠惠，张文栋.MEMS微惯性测量组合标定技术研究[J].传感技术学报，2008（7）：1169-1173.

[9]王欣.多传感器数据融合问题的研究[D].长春：吉林大学，2006.

[10]刘严岩.多传感器数据融合中几个关键技术的研究[D].合肥：中国科学技术大学，2006.

[11]解春香.异类多传感器数据融合技术的研究[D].沈阳：沈阳理工大学，2015.

[12]岳元龙，左信，罗雄麟.提高测量可靠性的多传感器数据融合有偏估计方法[J].自动化学报，2014（9）：1843-1852.