数形结合思想在高中物理解题中的应用

杨浩哲

（湖南省长沙市明德中学，湖南长沙 410000）

引 言

在物理的学习过程中，我们会经常遇到很多物理量与物理图形，“数”意指物理量，“形”意指用图形表达变量之间的关系图。很多物理量之间的关系，不仅可以采用公式来表示，还可以运用图形来表达[1]。

一、数形结合思想在物理解题过程中的体现

数形结合思想主张在解题的具体过程中通过数据与图形之间的转换，实现解题过程的清晰化、简单化。数据可以通过图形的样式来体现，图形可以使数据变量更加形象化；图形又可以通过数据的高低多少来表达，数据能够使得图形中表达的数据更加准确，该方法能够帮助我们在解题的过程中提高解题效率[2]。

数形结合思想最大的好处就在于能帮助我们解决计算量大且烦琐的问题，用简洁明了的图形表示出来。例如：

甲乙两人在长为L=84 m的游泳池里沿直线游泳，甲的速率V1=1.4 m/s，乙的速率V2=0.6 m/s，他们同时从水池的两端出发，来回共游了时间t=25 min，如果不计转向的时间，那么在这段时间内他们共相遇了几次？若他们同时从同一端出发，那么在上述时间内，他们共相遇了几次？

设甲、乙二人从游泳池的一端游到另一端所用时间分别为 T1、T2，

则T1=L/V1=84/1.4 s=60 s=1 min，

T2=L/V2=84/0.6 s=140 s=7/3 min，

比较 T1、T2可得：7T1=3T2，

所以经14T1（或6T2）即14 min时间甲、乙第一次同时回到各自的出发点。

以甲的出发点为坐标原点：

（1）甲、乙二人同时分别从游泳池的两端出发，则甲、乙二人的s-t图线分别如图1中实线和虚线所示。

图1

在0～25 min时间内两图线交点的个数即为甲、乙二人的相遇次数。

由图像可得，在0～14 min时间内二人相遇14次，由于14 min时两人同时回到各自的出发点，故14～25 min时间内二人重复0～11 min时间内的运动，相遇11次，所以25 min时间内二人共相遇25次。

（2）若甲、乙二人同时从同一端出发，用图像法亦可求得二人在25 min时间内共相遇21次。

甲、乙二人的s-t图线分别如图2中实线和虚线所示（解答过程不再累述）。

图2

当然，数形结合也不仅限s-t图的应用，用一些巧妙的几何图形也能快速解决物理问题，介绍一个有趣的定理：等时圆。

设一个圆O，A是圆O的最高点，X是圆上任意一点，一物体从A开始，沿AX下滑到X，所用的时间是相等的，都是从A自由落体到圆最低点用的时间。例如，从A到C所用的时间等于A到D所用时间，也等于从A到B（从A开始的自由落体运动）所用时间。如图3。

反之，将圆O倒置，亦成立。

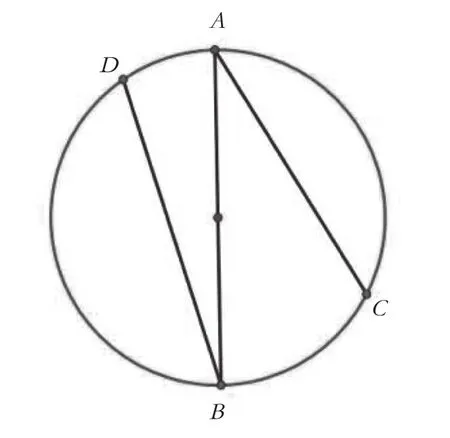
图3

有了这个性质，许多问题如比较运动时间长短之类的问题就变成了几何问题中寻找R值的问题。

例如，两光滑斜面的高度都为H，OC、OBD的总长度均为L，只是OBD由两个斜面连接而成，如图4所示，将甲、乙两个相同的小球从斜面的顶端O同时由静止释放，不计拐角的能量损失，问哪个球先到达斜面底端？

图4

本题的一般解法是用v-t图来讨论求解，但v-t图中的面积表示的是位移，而OC、OBD两斜面的长度相等，小球运动的路程相等，位移并不相等。因此要把v-t图理解为速率-时间图像。图线包围的面积表示的是路程。总之，解释起来颇费口舌。

我们可以构建如图5所示的等时圆，交OC于A点，交OB于B 点，由等时圆可知，Tob=Toa，由机械能守恒定律，有VB＞VA，VC=VD，所以VBD＞VAC，又因为两斜面的总长度相等，故XBD＜XAC，根据v=s/t得，TBD＜TAC，所以有T乙＜T甲，即乙球先到达斜面的底端。

图4

二、物理解题中采用数形结合思想对高中学生的要求

由前文可知，数形结合思想在物理解题的过程中很重要。在具体的学习过程中，例如，位移具体是指物体从最初的位置移动到第二个位置的运动，如果做出物体位移的有向线段图就能够更加直观地理解位移的概念，有向线段可以直观地呈现时间、距离、速度之间的关系。再如，在对动能定理的推导过程中，恰当的图形能够帮助学生更加直观地看出状态的改变，理解状态量与过程量之间的逻辑关系。同时，数形结合的方法还能够清晰地反映出各个矢量的方向与大小。很多结合图形来解答的题目是出题者比较青睐的对象。

结 语

在具体的解答与应用过程中，需要我们具有以下的能力：要做到会识别图形，明白图形所包含的物理意义；要学会构造图形，能够根据题目中传递的信息画出对应的图形，并且能够对图形进行转换；要会用图，能够采用图形分析具体逻辑过程，用图形解决具体的问题。在具体解答的过程中，需要我们自己去辨别，结合恰当的图形去解题。同时，还要求我们在解题的过程中有数形结合的意识。

[1] 王丹阳.数形结合思想在高中物理解题中的应用[J].科学大众(科学教育),2016,(01):22.

[2] 蔡冬莲.数形结合思想方法在数学教学中的应用分析[J].低碳世界,2016,(22):273-274.