以抽象思维发展为基点 提升数学课堂的有效性

李 建

（江西省丰城市石滩中心小学，江西丰城 331105）

引 言

在数学教学实践中，教师往往忽略了学生抽象思维能力培养，导致学生在问题分析、现实应用等方面有所欠缺。那么如何培养学生的抽象思维能力？我带领学生开展过无数次的教学探究活动，现根据自己多年的教学实践谈谈体会。

一、加强操作，手脑结合，梳理思维过程

在教学过程中，教师不但要让学生学会动脑，还要让学生学会动手。通过动手，能够让学生在操作活动中展开探究，从而找到问题的答案。因此，教师要多组织一些操作活动，带领学生从玩中学，在操作中学，借助动手操作，学生的各个感官协同参与，不但能够梳理思维过程，而且能够进一步提升抽象思维的能力[1]。

例如，在教学正方体和长方体的时候，对于小学生来说，几何图形中的立体空间过于抽象，不能建立一个具体清晰的直观印象，这就为教学带来一定的困难。尤其是正方体的展开图这个内容，学生在学习时，很难理解如何才能够“沿着虚线折叠后围成一个正方体”，学生也就不能用正方体的展开图来判断是否能够围成正方体。学生的困惑在于其对于正方体的展开图，并没有建构清晰的直观认知。也就是说，在学生的头脑当中，没有建立一个动态的形象，如果学生能够在头脑当中建立直观感知，那就有了立体空间的思维基础。此时该如何突破学生的认知困境呢？我特意引导学生展开了动手动脑的操作活动。

我将学生分成几个小组，同桌两人为一组进行合作。将一个正方体的纸盒剪开，并明确要求学生是沿着棱剪开。剪开之后就平放在桌面上。接着，我引导学生，将剪开的平面图还原成一个正方体的纸盒。学生完成了这两项操作之后，我让学生进行观察，并分组讨论。讨论的内容是：看一看展开图有什么不同，有什么相同。于是学生根据自己的操作，展开了讨论。有的学生经过讨论后发现，展开图的中间是4个，上下各是1个，但却具有不同点，那就是单独的两个有所不同，一个是对称的，另一个是错开的。根据学生的这个反馈，我进行引导，我们可以把这种上面一个，中间四个的图形叫作“141”型，并循着这个线索，继续引导学生思考，像这样的图形还可以继续分类，动手画一画，在自己的展开图上标出来。学生经过操作，能够将不同类型的展开图直观形象地呈现出来，我引导学生将这些直观图进行有序呈现、有序整理，其实也是对思维有一个有层次的梳理，学生得到了如下整理好的呈现图，如图1～6。

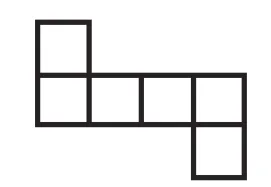
图1

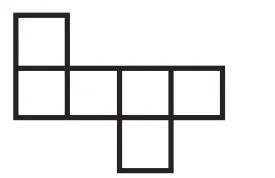
图2

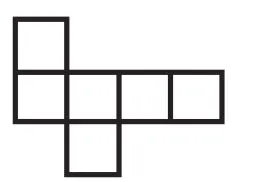
图3

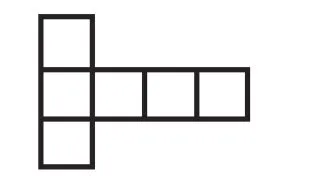
图4

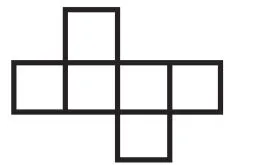
图5

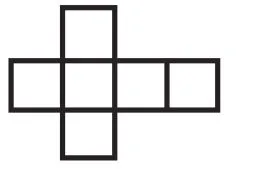
图6

我继续引导学生思考：想一想除了“141”型，还有其他的类型吗？再操作试试看。学生继续动手操作，发现还有一种类型，就是上面1个，中间3个，下边2个。学生称之为“132”型。学生自然而然地想要深入探究这种“132”型的展开图，还有哪些不同的分类。根据之前的有序探究模式，学生很快就整理好呈现图，如图7～9。

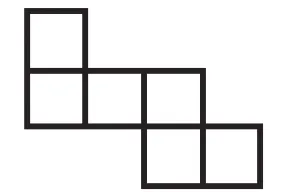
图7

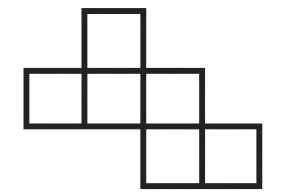
图8

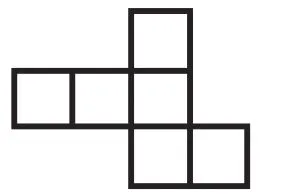
图9

还有学生通过操作很快就发现了另外一种展开图式，如图10～11，前者是“222”型，后者是“33”型。

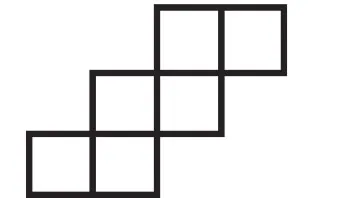
图10

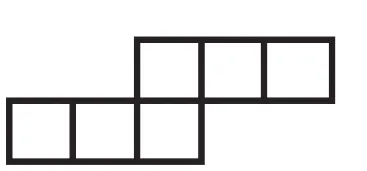
图11

在学生操作之后，我引导学生进行总结：想一想，将正方体展开，共有几种情形？这个展开的过程中，你有什么样的发现？说一说自己的思路。学生发现，正方体展开之后，共有11种图型，并且有一个规律，展开之后连成一排都不可能超过四个面。由此学生推论，如果一个图形有四个正方形可以围成一个“田”字，那么这个图形就不可能围成正方体。

以上教学环节，教师从直观形象的思维入手，借助动手操作，加强感官协作，组织学生展开探究。学生通过动手操作，在积极思考中不断梳理自己的思维过程，让抽象思维由杂乱走向有序，得到完善和发展。

二、数形结合，拓展延伸，提升思维品质

在小学数学教学中，数形结合是几何直观思维的有效体现。教师借助数形结合，能够帮助学生直观感知立体空间，由此，从具体到抽象展开延伸拓展，有效建构抽象的立体思维，提升学生的思维品质[2]。

图12

例如，在学完正方体之后，我出示了这样一道思考题：一块正方体木块六个面都涂上了颜色，现要将它切成64块大小相等的小正方体，如图12。

问：三面涂色、两面涂色、一面涂色的小正方体块分别有多少块？学生经过观察之后认为，正方体有8个顶点，所以三面涂色的就有8个；两面涂色的跟棱长有关联，所以两面涂色的有24个，一面涂色的跟长方体的面有关，所以一面涂色的有24个。在学生的直观观察之下，这个问题已经得到了解决。学生应该说已经掌握了正方体的特征。此时，我运用数形结合展开拓展延伸，对学生的抽象思维进行训练：

训练一：

如果要将这个正方体木块的每个面都均匀切上四刀，一共可以切多少个小正方体？其中，三面涂色的有多少个？一面涂色的有多少？没有涂色的有多少个？

学生在之前练习的基础上，展开解答，认为三面涂色跟顶点有关，无论怎么切，三面涂色都是8（个）；一面涂色（5-2）×（5-2）×6=54（个）；没有涂色的就是一个正方体，（5-2）³=27（个）。

训练二：

如果将正方体的木块，每个面均匀切n刀，一共可以切多少个小正方体？其中，三面涂色的有多少个？没有涂色的有多少？

根据具体数据，学生对训练二也有了解答：切n刀，每条棱上就有n+1个小正方体，三面涂色8个；没有涂色的其实形成了一个正方体，（n-1）3。

以上环节，教师借助数形结合，将抽象思维的要求难度加大，带领学生拓展延伸，从而最终实现了抽象思维的发展和提升。

三、丰富经验，结合实际，内化抽象思维

数学教学的本质，是培养学生将抽象思维内化为自己的技能，将数学思维应用在生活实践当中。这就需要教师结合实际，给学生提供机会，带领学生走出课堂，亲身经历应用数学分析问题、解决问题的实践过程，从而丰富学生的经验，内化学生的抽象思维。

例如，在教学计数单位“万”这一内容时，我结合学生的实际生活，要求学生预估图书馆藏书量，预估体育馆座位数量，在这个日常现实生活当中司空见惯的数学任务驱动下，学生不但丰富了经验，而且对“万”这个计数单位有了更深刻的认识。再如，在教学“公顷”这个概念后，我组织学生参观植物园，参观学校校园，参观周围的建筑，沿着大约一公顷面积的土地，四周走一圈。先从动态的角度，直观感知一公顷的面积大小，然后，让学生对菜农进行访问交流，了解一百平方米面积所种作物的产量和产值。通过这样的实际引导，让学生感悟到数学在现实生活当中的应用。

结 语

在数学课堂教学中，教师从学生的思维角度出发，组织操作探究活动，加强从直观到抽象的过渡，引导学生手脑并用，能够帮助学生提升抽象思维，使其更具有灵活性和逻辑性。

[1] 肖耕文.小学数学概念的教学策略与强化途径[J].江苏教育研究,2014,(23):59-61.

[2] 屠桂芳.过程与结果是数学活动的双翼[J].江苏教育研究,2016,(14):7-11,2.