螺旋离心泵内不稳定漩涡空化对出口压力的影响

邓育轩 ，纪燕飞 ，何立东 ，王灵德

（1.天华化工机械及自动化研究设计院有限公司，甘肃兰州 730050；2.北京化工大学，北京 100029）

1 前言

空化不仅对定常态的流体流动产生影响，而且空化还会影响流动的非定常特性或者动态响应特性［1～8］。对动态响应特性的改变会使流动内部出现不稳定性，这些不稳定性有漩涡空化和空化喘振等［9，10］，漩涡空化与压缩机中的旋转失速现象有些相似，空化喘振与压缩机喘振有些类似。这些不稳定特性会导致流量和压力的振荡，从而引起泵以及进出口管路的结构破坏［11～13］。

由于螺旋离心泵流道宽阔，螺旋离心泵叶轮区域发生的漩涡空化可以得到充分发展。本文以150×100LN-32型螺旋离心泵为研究对象，应用CFD软件对模型泵内的空化流动进行数值计算，分析模型泵内部漩涡空化流场气-液两相的分布规律，对充分发展的漩涡空化发展规律进行研究，捕捉完整的漩涡空化发展过程，并对数值计算结果进行试验验证，以期为深入研究漩涡空化及漩涡空化对水力机械性能的影响提供一定的理论依据。

2 几何参数

螺旋离心泵模型如图1所示，模型螺旋离心泵设计流量为160 m3/h，转速为1480 r/min，扬程为32 m。叶轮采用半开式叶轮，单叶片，叶片总包角为781°。

图1 螺旋离心泵模型示意

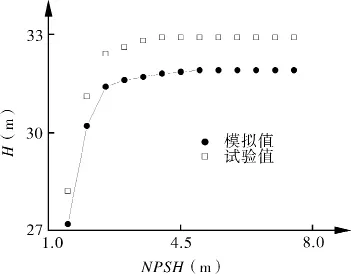
图2 螺旋离心泵空化特性曲线

3 数值模拟

采用Pro/E软件生成三维计算区域模型，如图1所示，模型由动叶轮、静止蜗壳、进口延伸段组成。采用ICEM软件对模型进行网格划分，总网格数为1203529。空化模型采用singhal等提出的完全空化模型［14］。输送介质为25℃的清水，25℃水的汽化压力为3169 Pa。近壁面处选用标准壁面函数，壁面边界条件设为绝热无滑移壁面，壁面粗糙度设为6.3 μm。进口边界条件设置为总压进口，液相体积分数为1，气相体积分数为0；出口边界条件为质量流量出口。通过调节进口压力改变进口的有效汽蚀余量，从而控制泵内部空化发生程度。先不激活空化模型进行均质两相流计算，取其结果作为空化流动计算的初始值，以提高计算的收敛速度和稳定性，各收敛残差设为10-5。叶轮每旋转3°作为一个时间步长，时间步长为0.0003375 s，计算过程叶轮旋转24个周期，每个旋转周期包含120个时间步，总计时间0.973 s，选取较为稳定的后几个周期的结果作为采样对象。

4 空化性能试验与预测

在水泵闭式试验台上对该型螺旋离心泵进行了空化试验。图2为模型泵在设计流量下的空化试验与数值模拟空化性能曲线，由图中可以看出数值模拟计算值与试验值的最大误差为4.69%，计算值与试验值曲线趋势一致，说明本文所采用的数值计算方法能够较为有效的预测螺旋离心泵的空化性能。

5 结果分析

5.1 流道内漩涡空化

螺旋离心泵叶轮与盖板之间存在间隙，由于叶轮工作面的压力大于背面，在该间隙处会有泄漏二次流产生，该二次流会在间隙附近产生漩涡，由于漩涡中心涡核处的压力较低，当旋涡中心的压力低于汽化压力时，就会发生漩涡空化。

图3为某时刻螺旋离心泵进口汽蚀余量为2.13 m时流道内空化区分布图，图中空化区的边界为空泡体积分数为0.1的等值面。

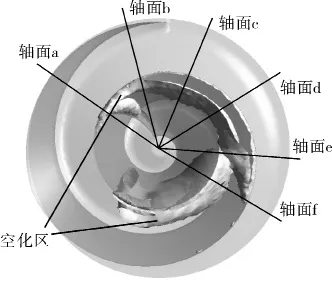
图3 不同包角对应的轴面

图4 所示为轴面a，b，c，d，e和f上的轴面流线与轴面上含气率大于0.1的空泡区分布图，如图 4（a），4（b）及 4（c）所示，随着包角的增大，由叶轮轮缘与盖板间的泄漏二次流动导致的漩涡开始出现并逐渐增大，相应的漩涡空化区逐渐增大；如图 4（d），4（e）及 4（f）所示，随着包角的进一步增大，由于泄漏二次流动的增强导致流道内出现了两个漩涡区，相应的出现了两个漩涡空化区，一个为近轮缘与盖板间隙处的漩涡空化区A，另一个为远离轮缘与盖板间隙处的漩涡空化 区B。

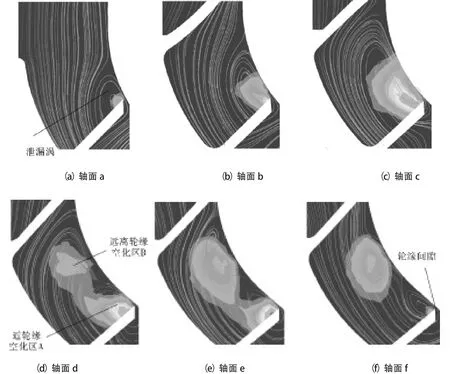
图4 不同轴面上的流线与含气率分布

图5 为一个叶轮转动周期内3个连续时刻流道内空泡体积分数为0.1的等值面图，图5（a）中空化区A，B分别为与图4（d）相对应的近轮缘空化区A、远离轮缘空化区B，空化区C为远离轮缘空化区的初生状态；由图5可以看出，随着叶轮的转动，从t1到t3时刻，远离叶轮轮缘与盖板间隙的漩涡空化区B有一个漩涡空化形成-发展-分离过程［15，16］。

图5 不同时刻流道内空泡体积分数等值面

5.2 不稳定漩涡空化对出口压力的影响

图6 为螺旋离心泵在不同工况下连续4个整周期内的泵出口压力脉动时域图。由于螺旋离心泵只有一个叶片，在叶片与隔舌的动静耦合作用下，每个周期泵出口压力波动为一个完整的正弦曲线。图6（a）为有效汽蚀余量NPSH为3.05 m时泵出口压力脉动图，此时泵叶轮区域有空化发生，但没有出现如图5所示的流道中部远离轮缘的漩涡空化区B。图6（b）为有效汽蚀余量NPSH为2.13 m时泵出口压力脉动图，由前文可知，该工况下叶轮区域会出现漩涡空化初生-发展-分离的过程；图6（b）中时刻t1和t3与图5中的时刻t1和t3相对应，叶轮转动一周所需时间为4.05×10-2s，设该时间为T，分别以t1和t3为起始点，每经过T/2标记一个点；由图6（b）可以看出，t1时刻之前，出口压力处于一个上升阶段，从t1时刻开始，出口压力开始出现下降，直到t3时刻压力又恢复上升趋势，如前文所述，从t1时刻到t3时刻有一个漩涡空化初生-发展-分离的过程，这说明发生该过程会对泵内部的流场产生扰动，从而影响到出口瞬时压力；从t1时刻起，叶轮转过半个周期之后，在t1+T/2时刻又发生了上述漩涡空化初生-发展-分离的过程，到t3+T/2时刻该过程结束，在t1+T/2时刻之前出口压力处于一个下降的阶段，对比图6（a）和图6（b）可以看出，该过程的发生会使出口压力降低到更低，即图6（b）中t3+T/2时刻所处的波谷位置要低于图6（a）中相应的波谷位置；再经过T/2时间，又会发生一次上述过程，相应的会有出口瞬时压力的降低，由图6（b）可以看出，叶轮每转过一周，该过程发生2次。

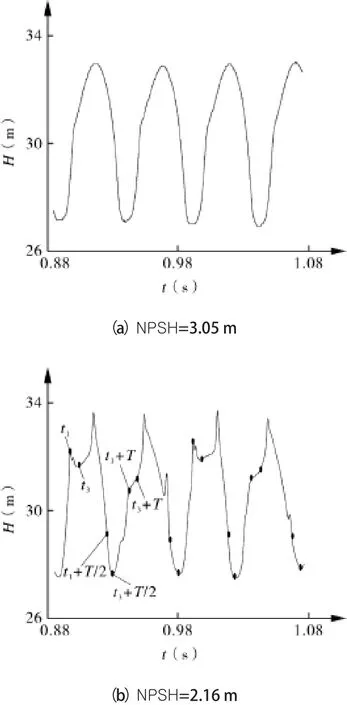
图6 螺旋离心泵出口压力波动时域图

5.3 漩涡空化的发展对扬程的影响

图7 所示为不稳定漩涡空化对应的扬程曲线。从图可见，设计工况下泵内没有空化发生；进口汽蚀余量为2.13 m时，螺旋离心泵内部远离叶轮轮缘与盖板间隙的漩涡空化区有一个漩涡空化形成-发展-分离过程，大约每隔2.024×10-2s该过程发生1次，该工况下的扬程曲线上的点状标记为每次漩涡空化形成-发展-分离过程的起始点。对比2条曲线可以看出，由于发生了漩涡空化形成-发展-分离过程，在进口汽蚀余量为2.13 m时，当漩涡空化形成-发展-分离过程起始点位于扬程曲线上升阶段时，会导致扬程曲线在上升过程中出现一个回落，当漩涡空化形成-发展-分离过程起始点位于扬程曲线下降阶段时，会导致扬程曲线的波谷位置更低，这说明该工况下的扬程曲线是漩涡空化形成-发展-分离过程特有的泵扬程波动趋势。

图7 不稳定漩涡空化对应的扬程曲线

6 结语

随着有效汽蚀余量NPSH的降低，由流经轮缘间隙的二次流引起的漩涡低压区会在轮缘附近生成空化区，由于轮缘间隙两侧的周期性压力波动，轮缘间隙附近的漩涡会发生周期性脱落，脱落的漩涡在流道中部又会导致新的空化区生成，该空化区会占据大部分流道，造成扬程大幅下降；伴随漩涡脱离，新漩涡空化的初生-发展-分离过程会使泵出口压力产生不规则的波动。

在一定工况下，螺旋离心泵叶轮区域会出现周期性的漩涡空化初生-发展-分离的过程，这意味着该泵内部漩涡空化的初生在一定程度上是可控的，并且漩涡空化的初生、发展过程会相对稳定的重复发生，所以螺旋离心泵是一个比较好的用于研究漩涡空化的平台，可以基于螺旋离心泵来进一步研究水力机械内部的漩涡空化特性及研究空化的初生、发展对水利机械性能的影响。

［1］ Adrian S，Romeo S R，Liviu E A，et al.A new approach in numerical assessment of the cavitation behaviour of centrifugal pumps［J］.International Journal of Fluid Machinery and Systerms，2011，4（1）：104-113.

［2］ Medvitz R B，Kunz R F，Boger D A，et al.Performance analysis of cavitation flow in centrifugal pumps using multiphase CFD［J］.ASME Journal of Fluids Engineering，2002，124（2）：377-383.

［3］ Rudolf B，Bernd S，Matevz D，et al.Unsteady cavitation at the tongue of the volute of a centrifugal pump［J］.Journal of Fluids Engineering，2010，132（6）：061301.

［4］ 李仁年，陈昊，韩伟，等.大颗粒下螺旋离心泵内运动特性数值模拟与分析［J］.流体机械，2016，44（7）：18-21.

［5］ 杨敏官，倪丹，李忠，等.791翼型非定常空化流动数值计算研究［J］.流体机械，2015，43（2）：17-23.

［6］ 张华，陈斌，施卫东，等.单叶片螺旋离心泵内部流场数值计算及油膜试验研究［J］.排灌机械工程学报，2016，34（5）：381-385.

［7］ 李仁年，毕祯，黎义斌，等.诱导轮偏转角对离心泵叶轮空化性能的影响［J］.排灌机械工程学报，2016，34（6）：461-469.

［8］ 吴玉珍，李龙贤，金志磊，等.数值模拟在高速泵汽蚀性能预测中的应用［J］.化工设备与管道，2015（3）：52-56.

［9］ Duplaa S，Coutier-Delgosha O，Dazin A，et al.Experimental study of a cavitating centrifugal pump fast startups［J］.Journal of Fluids Engineering，2010，132（2）：021301.

［10］ Jeanty F，Andrade J D，Asuaje M，et al.Numerical simulation of cavitation phenomena in a centrifugal pump［C］.Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting，2009：331-338.

［11］ Hydraulic Institute .Hydranlic institute standards for centrifugal，rotary & reciprocating pumps［M］.14th ed.Parsippany，NJ：Hyraulic Instite，1983.

［12］ Senocak I，Shy W.A pressure-based method for turbulent cavitating flow computations［J］.Journal of Computational Physics，2002，176（2）：363-383.

［13］ 明廷峰,郭井加,曹玉良,等.离心泵内流场空化特性的数值模拟研究［J］.机电工程,2016,33(6):643-647.

［14］ Singhal A K，Athavale M M.Mathematical basis and validation of the full cavitation model［J］.Journal of Fluids Engineering，2002，124：617-624.

［15］ 邓育轩，李仁年，韩伟，等.螺旋离心泵内非定常漩涡空化的计算与分析［J］.华中科技大学学报，2014，42（9）：118-121.

［16］ 潘中永，袁寿其.泵空化基础［M］.镇江：江苏大学出版社,2013.