基于叶轮压水室特性匹配的离心泵作透平的性能预测
黄 思,何 婧,舒亚篮,区国惟
(1.华南理工大学,广东广州 510640;2.广东省佛山水泵厂有限公司,广东佛山 528000)
1 前言
泵作透平(Pump as turbine, PAT)是将水泵反转成为水轮机模式,通过高能流体与泵的出口连接驱动转轮,带动发电机工作,实现流体能向电能的转化[1~6]。PAT是一种方便快捷的能量回收装置,在合成氨、加氢裂化、城市循环水系统和小型水力发电等工业领域有着广泛的应用;对于边远地区的小型水力发电问题,PAT也是一个较理想的解决方案。
有关PAT的选型和性能预测方面的研究,国内外学者主要是依据转轮欧拉方程的理论推导结合实验数据进行修正,得到水泵正转和反转模式的性能换算方法[7~11],这些研究未能考虑压水室(蜗壳)的水力性能尤其是转轮与压水室的匹配关系,在应用上往往受到各自条件的限制。本文从PAT的转轮和压水室特性方程出发,根据它们之间的匹配关系确定匹配工况点即最优工况点,为PAT的选型及应用提供理论依据。
2 理论分析
水泵和PAT的水力性能是由叶轮和压水室共同决定的,二者的最优匹配问题是研究泵和PAT特性的重点。以下使用下标P代表离心泵的正转模式,T代表反转模式即PAT模式。对于离心泵正转模式,叶轮进出口速度三角形如图1(a)所示,进口下标是1,出口下标是2。
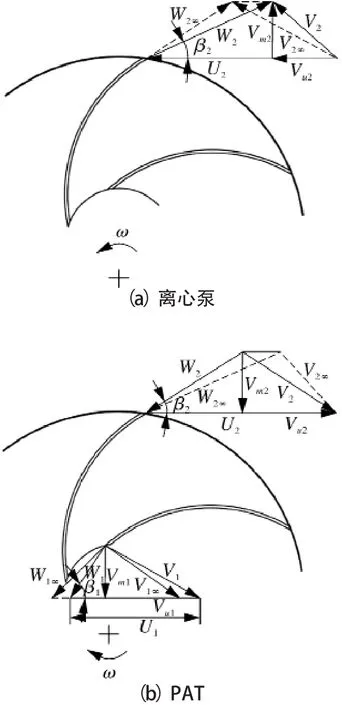
图1 离心泵正反转模式下叶轮进出口速度三角形关系
扬程系数ψ和流量系数φ的定义式为:式中 Ht——理论扬程
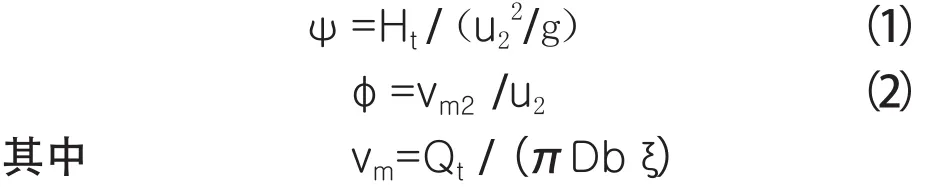
u——叶轮圆周速度
vm——轴面速度
Qt——理论流量
b——叶轮的宽度
ξ——叶片的堵塞系数
叶轮的无量纲特性方程为:
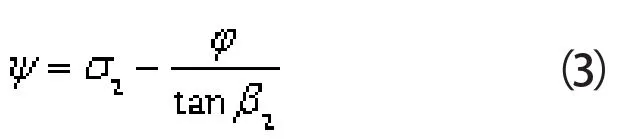
式中 σ——叶轮滑移系数
β——叶片安放角
压水室的无量纲特性方程为[12]:
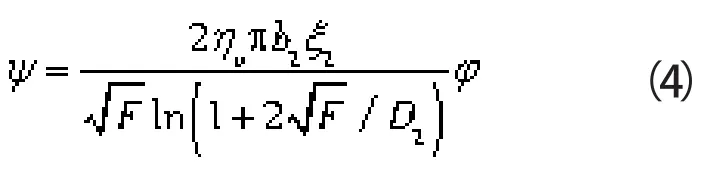
式中 ηv——水泵的容积效率
由上表可以看出,经过不同年限培养的人员,对自己预期达到党员条件的时间有明显的趋势性变化:列为入党积极分子2年以内者,一半以上(55.8%)认为自己在1~2年内就可以达到基本成熟条件;相反,列为入党积极分子5年以上者,却有50%的人认为自己需要再被培养5年以上才可以达到基本成熟条件。
F——压水室第八断面面积
离心泵叶轮与压水室的匹配工况点(图2的交点A)通过联立叶轮和压水室特性方程(3)、(4),求解得到:
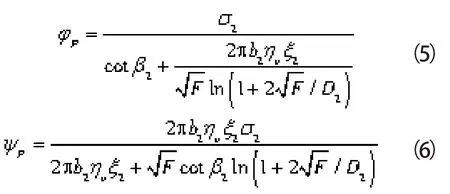
则离心泵的匹配工况点流量Qp和扬程Hp预测值由下式得到:
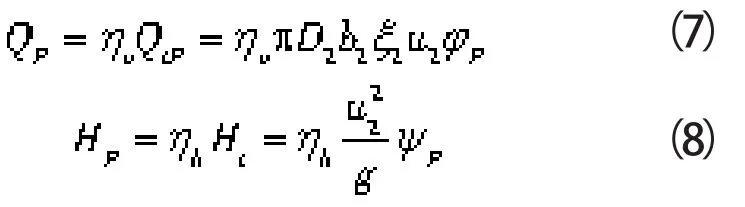
式中 ηh——水泵的水力效率

图2 离心泵正反转模式下叶轮和压水室的特性匹配
按上述方法研究图1(b)所示的PAT模式下转轮和压水室特性的匹配问题。PAT转轮的进口下标是2,出口下标是1,假设PAT的水力效率、容积效率、机械效率、蜗壳特性、滑移系数、堵塞系数与离心泵正转模式下对应的参数相同[10]。
有限叶片数下透平的理论扬程Ht为:
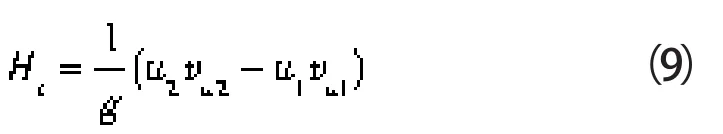
由图1可得,绝对速度的周向分量vu为:
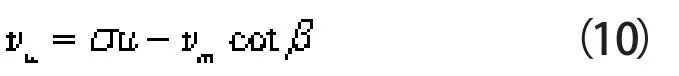
将式(1)、(2)代入式(9)、(10)中,并联立求解,得到:
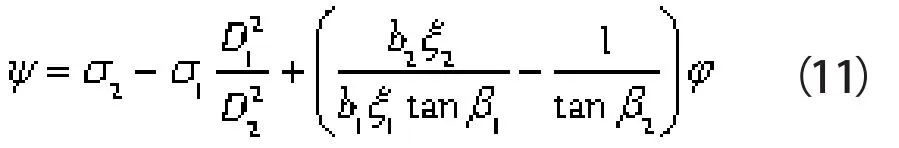
上式右侧括号内第二项相对第一项较小可忽略不计,则式(11)可简化为:

联立式(4)与式(12),求得图2中PAT匹配工况点B坐标为:
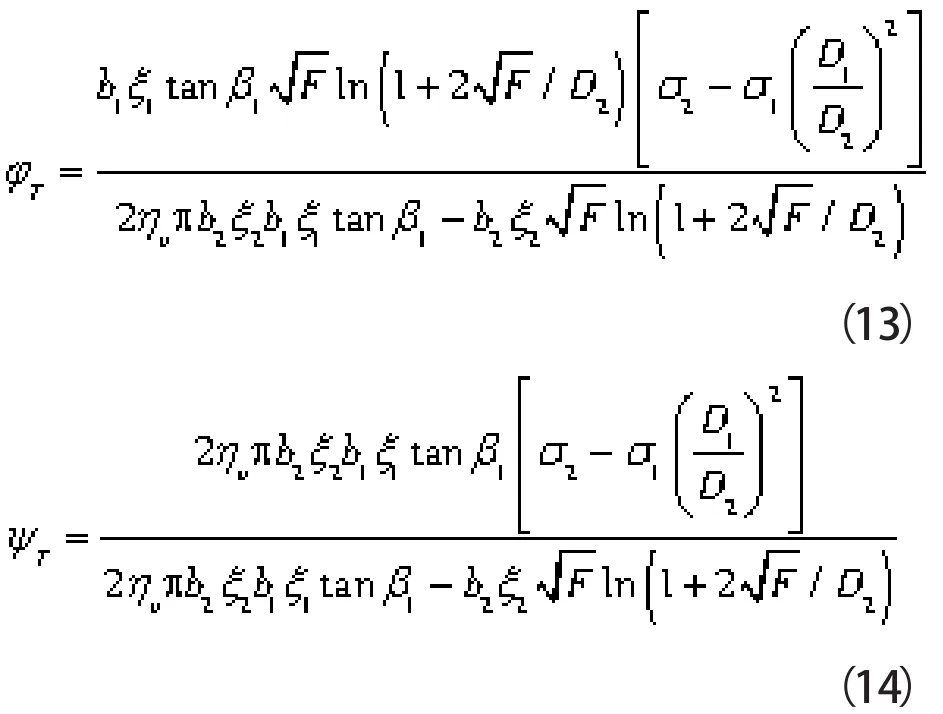
则离心泵和PAT最优工况下流量和扬程的换算系数q和h为:
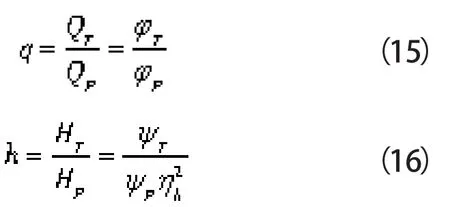
式(15)和式(16)是考虑了PAT转轮与压水室特性的匹配关系,仅需知道转轮和压水室的几何参数而不受比转速的限制,具有通用性和实用性。
3 工程案例及试验验证
为验证PAT理论预测方法的有效性,选取IS100-65-200型离心泵进行正反转模式下的试验验证,该离心泵设计工况参数为:流量Q=50 m3/h,扬程H=12.6 m,转速n=1480 r/min,比转速ns=95.2。离心泵叶轮进口直径D1=90 mm,出口直径D2=203 mm,进口宽度b1=36 mm,出口宽度b2=16 mm,叶片数z = 6,叶片进口安放角β1=25°,轴面流线与水平夹角λ1=73°,进口厚度δ1=3 mm,出口安放角β2=35°,出口圆周方向厚度Su2=9 mm,蜗壳第八断面面积为F=2417 mm2。预测计算中所涉及的参数如表1所示。

表1 离心泵及PAT性能预测涉及的参数
将上述参数代入式(5)和(6)计算得到离心泵的无量纲匹配工况点为φP=0.1163,ψP=0.5336。由式(7)、(8)转换得到离心泵最优工况点参数为QP=59.56 m3/h,HP=11.55 m。同理,由式(13)、(14)求得PAT的无量纲匹配工况点为φT=0.1538,ψT=0.7056,由式(15)、(16)转换得到PAT的最优工况点参数为QT=78.76 m3/h,HT=20.79 m。
离心泵和PAT的性能测试是在某水泵厂的试验台完成。该试验台(如图3)采用多功能参数测量仪的微机自动测试系统,各测试仪表参数如表2所示,整套系统达到国家B级精度水平。试验时PAT进口连接增压后高压水头,出口返回水池,与PAT直连的是一台负荷泵。PAT的进出口位置均有压力表读取压力值,流量值由涡轮流量计读取,转速和转矩值由转速扭矩仪测得。通过调节旁通阀和PAT出口阀门,读取同一转速下PAT的不同运行工况点参数,将其绘制成图4和图5所示的外特性曲线。
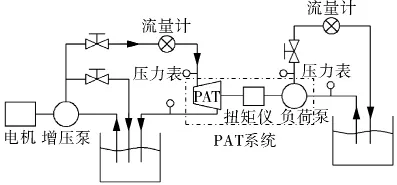
图3 离心泵—PAT测试系统
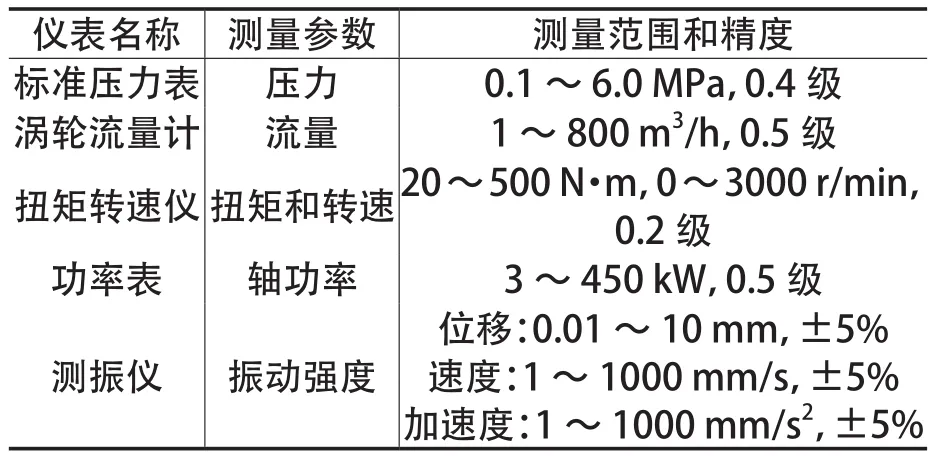
表2 水泵—PAT性能测试仪表
表3给出了理论预测的水泵及PAT匹配工况点参数与从图4和图5读取的最优工况点参数实测结果的对比情况。由表3可见,无论是水泵模式还是PAT模式,无论是流量值还是扬程值,预测结果和实测结果的误差都在工程允许的范围内,说明本文提出的性能预测方法是切实可行的。
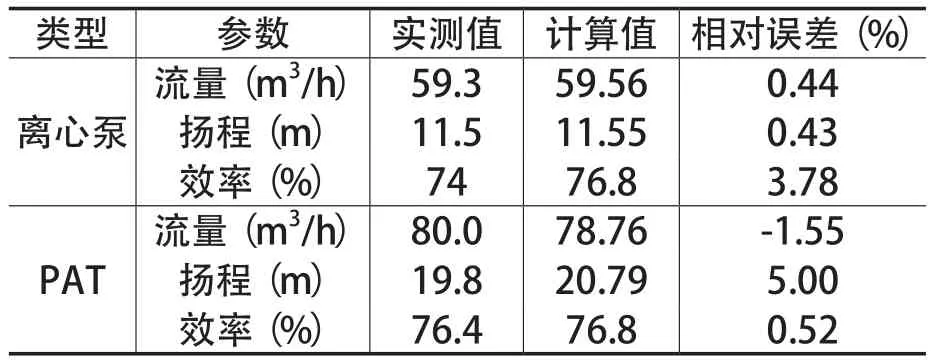
表3 离心泵及PAT最优工况点参数预测与试验结果的对比
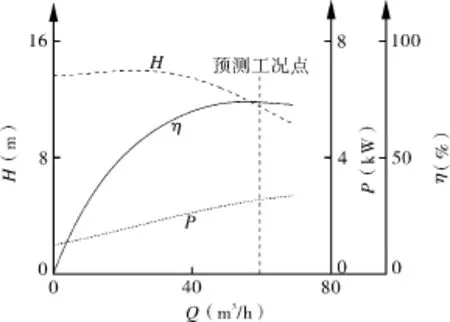
图4 离心泵实测的性能曲线
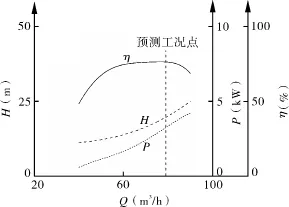
图5 PAT实测的性能曲线
4 结论
(1)本文从离心泵在反转模式(PAT)下的欧拉方程出发,根据转轮与压水室的匹配关系,预测匹配工况点即最优工况点参数,预测方法和结果得到了试验结果的验证。
(2)通过已知叶轮和蜗壳的几何参数可得到不受比转速限制的离心泵正反转模式下性能换算系数的表达式,具有通用性和实用性,这将为PAT的选型及应用提供理论依据。
[1] Jain S V, Patel R N.Investigations on pump running in turbine mode:a review of the state-of-the-art[J].Renewable and Sustainable Energy Reviews,2014,30:841-868.
[2] Williams A A.Pumps as turbines for low cost micro hydro power[J].Renewable Energy,1996,9(1): 1227-1234.
[3] 王桃,孔繁余,何玉洋,等.离心泵作透平的研究现状[J].排灌机械工程学报,2013,31(8):674-680.
[4] 杨军虎,张雪宁,王晓晖,等.能量回收液力透平的研究进展[J].化工机械,2012,38(6):655-658.
[5] 戴洪球.液力能量回收透平的性能试验[J].石油化工设备技术,1988,9(3):43-45.
[6] 黄思,陈宇,宿向辉.离心泵作水力透平起动过程的非定常流场模拟计算[J].水泵技术,2015(5):25-30.
[7] 盛树仁,房壮为.可逆式水轮机转轮水力设计的探讨[J].大电机技术,1983(5):41-48.
[8] 刘甲凡.泵作水轮机运行的特性分析[J].农业机械学报,1997,28(3):20-24.
[9] Williams A A.The turbine performance of centrifugal pumps:a comparison of prediction methods[J].Proceedings of the Institution of Mechanical Engineers,Part A:Journal of Power and Energy,1994,208(1):59-66.
[10] Derakhshan S,Nourbakhsh A.Theoretical,numerical and experimental investigation of centrifugal pumps in reverse operation[J].Experimental Thermal and Fluid Science,2008,32(8):1620-1627.
[11] 史广泰,杨军虎.离心泵用作液力透平叶轮出口滑移系数的计算方法[J].农业工程学报,2014,30(13):68-77.
[12] 关醒凡.现代泵理论与设计 [M].北京:中国宇航出版社,2011.
[13] 周林玉.偏离工况下离心泵的压力脉动和振动分析[J].流体机械,2015,43(2):52-56.
[14] 翟之平,张钊源,杨忠义,等.油田用离心泵汽蚀性能的数值分析与试验[J].流体机械,2015,43(8):1-4.
[15] 吴玉珍,李龙贤,金志磊,等.数值模拟在高速泵汽蚀性能预测中的应用[J].化工设备与管道,2015,52(3):52-56.
[16] 李伟,杨笑瑾,马东华.镍基合金换热管分段式机械胀接试验[J].压力容器,2015,32(9):75-79.
[17] Karassik I J,Messina J P,Heald C C,et al.Pump handbook[M].McGraw-Hill, 1976.
——“AABC”和“无X无X”式词语

