一种新型液体输送泵的输送性能模拟

俞翼翔，谢 令，唐黎明，陈光明

（浙江大学制冷与低温研究所，浙江省制冷与低温技术重点实验室，浙江杭州 310027）

1 前言

泵是一种以输送流体或使液体增压为目的的机械，是一种以液体为工作介质进行能量转换的装置。泵作为通用机械之一，在日常生活、工农业生产、电力、船舶、纺织、国防等部门中发挥着重要作用［1］。根据美国太平洋西北国家实验室的调查，当前泵系统耗电量大约为全球工业总用电量的20%［2］。和国外相比，我国自行生产的泵类产品效率平均低3%～5%［3］。在能源危机日益严峻，节能减排势在必行的大环境下，泵的节能研究至关重要。

近年来，国内外专家为了改善泵的节能性能提出了诸多新型泵结构并在此基础上不断改进，但是取得的效果并不是很突出［4～7］。浙江大学制冷与低温研究所提出了一种新型的液体输送泵，该输送泵通过高低配盘以及转子实现液体从低压区输送到高压区的目的［8］。本文运用CFD对这种新型液体输送泵进行建模研究，模拟测试新型液体输送泵的一些基本性能，对新型液体输送泵的试验研究以及结构改进具有重要的指导意义。

2 新型液体输送泵介绍

本文所提出的新型液体输送泵的工作原理如图1所示。

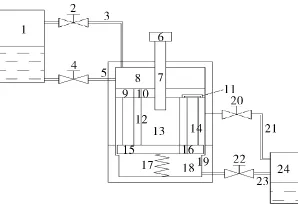
图1 新型液体输送泵工作原理示意

该液体输送泵泵体主要分为3部分：与低压腔相连的低压区、转子通道、与高压腔相连的高压区。其中，转子通道同时起着周期性隔离高低压腔压力和间歇性平衡高低压腔压力的作用，同时实现液体的输送。转子转动过程中，会交替与高低压腔对接。首先，低压液体通过低压进液管进入低压腔；当转子与低压腔对接时，转子内的气体压力与低压腔的压力进行平衡，低压腔内的液体由于重力作用进入转子通道；由于转子转动，一定量的液体进入转子通道后，转子离开与低压腔对接的位置并与低压腔隔离后逐渐与高压腔对接，转子内压力逐渐与高压腔内的压力平衡，转子内的液体通过重力自由下落至高压腔内；高压腔内的液体通过高压出液口流入高压储液罐。此为新型液体输送泵的一个工作循环，实现了液体从低压输送到高压的目的。

这种新型液体输送泵的输送原理与传统液体输送泵最大的不同在于传统液体输送泵是通过对液体加压来实现液体从低压到高压的输送，新型液体输送泵主要是通过液体的重力实现低压到高压的输送。但是新型液体输送泵需要一个外接的高压源。相比电能，高压源更为廉价，可以通过低品位热能得到，因此这种泵的原理十分值得关注。

传统液体输送泵对液体加压的过程消耗电能巨大，而新型液体输送泵的主要耗能在于转子的回转耗能，只需克服转子与高/低配盘之间的摩擦阻力，与传统液体输送泵耗能相比较，所需的电能更少，因此新型液体输送泵拥有较大的节能潜力。

3 CFD模型建立

CFD计算具有适应性强、应用面广等优点，又由于其很大程度上不受物理模型和试验模型的限制，CFD计算现在越来越成为预测和指导试验的重要手段。由于本液体输送泵属于一种新型的泵形式，在研究过程中结合CFD计算来优化结构以及指导试验方面具有较大的价值。

本文中的CFD计算采用SolidWorks进行建模，导入DM，运用ICEM的O型块划分全六面体网格，最后导入Fluent计算分析。本文模拟的过程中包含转子转动问题，因此在模拟过程中涉及动网格的生成，需要采用Fluent中的滑动网格模型。

3.1 模型假设及几何结构

为了在建模过程中简化计算同时对模拟结果影响不大的情况下，做出如下假设：

（1）转子通道与低压配流孔对接后，通道内气体的高压能够经平衡孔快速平衡，因此可以认为液体从低压配流孔输送到转子通道中的过程为等压过程；

（2）转子通道在与高压配流孔对接的时候，通道内液体由于压力的平衡能够在自身重力的作用下经高压配流孔完全地进入高压腔内，这样液体输运能力就取决于转子通道与低压配流孔的对接过程。

在以上假设下，建立的3D模型见图2。

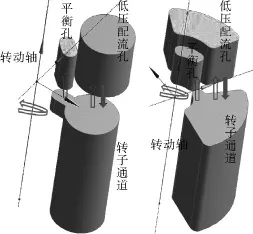
图2 转子通道和低配盘的3D模型

3.2 控制方程

计算流体力学的基础是守恒方程。在输送流体泵模型中，主要包含质量守恒方程、能量守恒方程以及动量守恒方程，其方程形式如下所示：

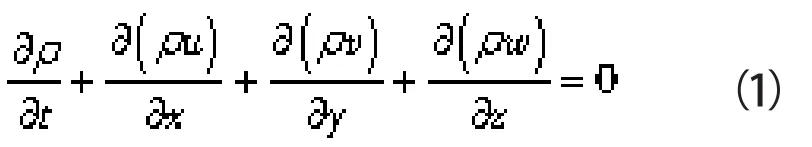
式中 ρ——流体密度

u,v,w——流体在x,y,z方向上的速度

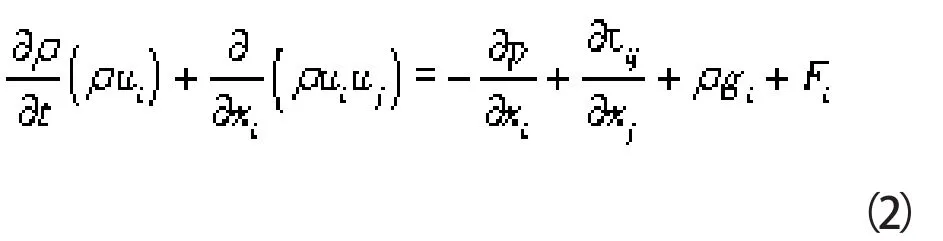
式中 p——静压

τij——应力张量

ρgi，Fi——i方向上重力及外部体积力

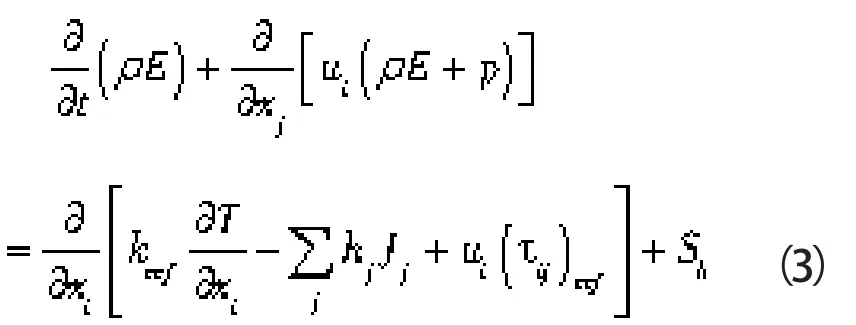
式中 keef——有效导热系数

Jj——组分j的扩散流量

Sh——化学反应热以及其他体积热源项

3.3 边界条件及计算参数

模拟过程中采用的边界条件以及计算参数介绍如下：

（1）模拟中输送的液体选用水，高压气体选用空气，水和空气之间的表面张力取0.072 n/m［9］。

（2）低压配流孔和平衡孔上表面分别与低压储液罐的上下相连，因此压力为低压压力值且数值保持不变，设此为压力入口边界；低压配流孔和平衡孔下表面在转子转动过程中与转子通道的上表面对接，实现气液交换，这3个表面皆为interface边界，其他表面均设为wall边界。

（3）初始状态下，低压配流孔、平衡孔、转子通道压力平衡，都为低压压力值，低压配流孔充满液体，转子通道以及平衡孔内充满气体。

（4）压力采用PRESTO离散格式，动量采用二阶迎风格式、体积分数则采用一阶迎风格式。

（5）质量、速度、动量及体积分数的收敛残差判别依据设为10-3。

4 模拟结果分析与讨论

根据本文以上模型，得出了对接时间对输送液体质量的影响、转子材料（亲水性、疏水性）对输送液体质量的影响以及圆形和扇形两种通道形式对输送液体的影响。

4.1 输送液体质量随对接时间的影响

圆形通道转速为85 r/min时的对接过程中，液体输送质量随时间的变化曲线如图3所示。

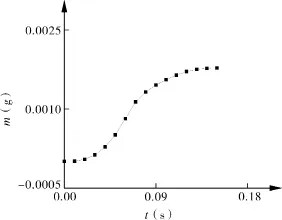
图3 输送液体质量随对接时间的影响

模拟结果显示，当转子通道与低配盘通孔刚开始对接时，液体并没有直接进入到转子通道中，这是由于液体与通道之间存在表面张力，同时，液体重力并不能完全克服表面张力，形成液塞现象，因此，转子内的液体流量为零。随着对接时间增长，对接面积逐渐增大，重力的影响逐渐超过了表面张力，液体逐渐流入通道，并且存在一个加速流入的过程。当转子通道与低配盘通孔完全对接时，液体流量达到最大值，之后随之缩小，直至为零。

由于液体输送过程中存在液塞现象，因此转子通道的尺寸有一个最小半径，当转子通道半径小于这个最小半径时，无法实现液体的输送。

4.2 同一通道形式下转子材料对输送流体质量的影响

气液交换过程起始和结束时会存在一个液塞过程，主要是由于表面张力引起的，而不同材料的转子，表面张力不同，因此不同材料对液体输送的影响不同。在模拟计算中，转子材料对输送流体质量的影响，主要是通过改变转子表面接触角（模拟中采用30°和120°），观察对接过程，得出转子输送液体质量随时间的变化。转子转速为100 r/min时的结果如图4所示。

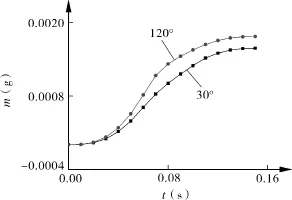
图4 不同材料圆形通道转子输送液体质量随时间变化

转子材料的不同（亲水与疏水）影响的主要是实现汽液交换与对接过程的时间差（液塞时间长短）。从图4可以发现，亲水转子的气液交换时间要早于疏水材料的气液交换过程。在图中呈现的结果就是疏水材料与亲水材料相比，克服摩擦阻力所需的时间更长。由于对接总时长相一致，亲水材料总液体输运量相较疏水材料也更多。扇形结构有类似规律。

4.3 不同通道形式对输送流体质量的影响

在此次模拟中，选用的通道形式有扇形和圆形2种，不同转子通道形式对输送液体质量的影响见图5。

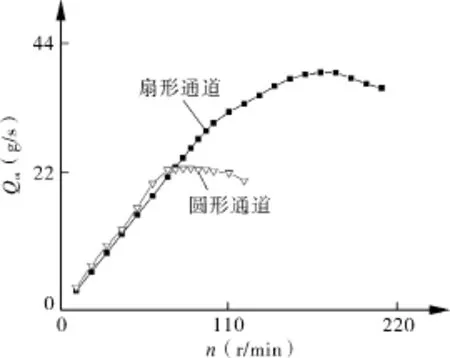
图5 不同通道形式对输送液体质量的影响

在转速较低时，扇形和圆形通道的流体输送量基本一致，可以认为在转速较低时，通道的对接时间足够长，从而可以忽略扇形通道和圆形通道不同通道形式之间对接时间的影响。而当转速提高到一定程度后，对接时间的长短会对流体流量造成较大影响，而扇形通道的无流量运输对接时间（液塞时间）比圆形短，因此，在一定的转速后，扇形通道对液体的输送量要大于圆形。同时每种通道形式达到一定转速后，每个对接过程时间过短，无法使得通道得到全部有效利用，因此流量输运达到一个极值后下降。因此每种通道形式均存在一个最佳转速。转速达到最佳前，由于通道均得到全部利用，随着转速增加，流量几乎呈线性增长；转速大于最佳转速后，继续增大转速，输送的液体流量反而减小。

5 结论

（1）液体输送周期始末存在一个明显的克服表面张力的过程，在这个过程中，液体输送量基本为0，而在克服表面张力之后会有一个明显加速下流以及一个减速下流的过程。

（2）输送的液体与转子材料的接触角对液体输送有一定的影响，表现在对接过程中克服表明张力所需时间的长短，一般接触角大于90°（相亲）的材料液体输送性能优于接触角小于90°（相疏）。

（3）新型液体输送泵转子通道形式对于液体输送质量具有十分重要的作用，同样的转子半径下，扇形通道与其他形状的通道形式相比，具有最优的液体输送效率。

［1］ 国家经贸委资源节约综合利用司.关于风机水泵节能改造的主要思路［J］.电子节能,1998(3)：5-6.

［2］ Hammerstorm D J,Ambrosio R,Brous J,et al.Pacific Northwest Grid Wise testbeddemonstration project［R］.Part I: Olympic peninsula project,Pacific Northwest Laboratory, PNNL17167,2007,5.1-5.6.

［3］ 王立.我国泵系统节能的现状及发展前景［J］. 水泵技术，2012（1）：28-30.

［4］ Van de Pol F C M,Wonnink D G J.A thermopneumaticmicropump based on micro-engineering techniques［J］.Sensors and Actuators, 1989(17):139-143.

［5］ OKAYASU KENJI. Heat Drive Pump. JpnPatentJP-63001773A［P］. 1988-01-06.

［6］ Stemme E, Stemme G. A valveless diffuser/nozzlebased fluid pump［J］. Sensors and Actuators A:physical, 1993, 39(2): 159-167.

［7］ Olsson A, Stemme G, Stemme E.A valve-less planar fluid pump with two pump chambers［J］. Sensors and Actuators A: Physical, 1995, 47(1): 549-556.

［8］ 林玮.一种新型液体输送泵的理论与实验研究［D］. 杭州：浙江大学 , 2014.［9］ 任文辉, 林智群, 彭道林. 液体表面张力系数与温度和浓度的关系［J］. 湖南农业大学学报 : 自然科学版 , 2004, 30(1): 77-79.