风圈式风量调节阀阻力特性的模拟研究

陈永平，王海桥，陈世强，田 峰

（1.湖南科技大学，湖南湘潭 411201；2.中铁隧道勘测设计院有限公司，北京 100000）

符 号

ρ——流体密度，kg/m3

ui，uj——流体的速度分量，m/s

ε——流体微元体上的压强，Pa

μ，μt——动力黏度、湍流黏度，Pa·s

k——湍流动能，m2/s2

ε——耗散率，m3/s

σk，σε——k，ε方程对应的 Prandtl数

Δp——阀门前后压差，Pa

v——管内流速，m/s

ρ——流体密度，kg/m3

a，b，c——系数

1 前言

调节阀种类繁多，不同的调节阀内部结构及阻力特性差异很大[1]。风圈式风量调节阀，通过多个重叠弧形钢片的开合控制过流通道的大小，做到对流量的无极调节，并且过流通道是圆形的[2]，见图1。利用数值模拟方法可以分析阀门的阻力系数，为优化阀门结构，减小阻力系数提供方便[3～8]。阻力系数是评价阀门性能的重要参数。阀门阻力系数的大小直接影响着管道系统的使用，是设计者和用户最关心的参数之一[9～11]。

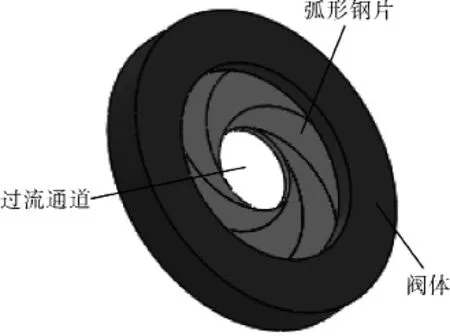
图1 风圈式风量调节阀

在气体输送等工程实际中，当自动控制子系统调节调节阀开度时，首先通过测定管道的流速形成反馈信号，然后对比当前值与预设值，得出调大或调小判断，输出调节信号，如此循环，逐步当反馈信号逼近调节信号，这种调节过程费时，管道运行参数波动大。如果自动控制逻辑程序内嵌了阻力系数与阀门开度半径的函数关系式，将可以比较精确的得到不同开度下的阻力系数，将大大节省阀门调节时间，减小对管道运行参数的影响，有利于延长自动调节阀的运行寿命。

本文将对风圈式风量调节阀建立物理模型，对该阀门的流场及阻力特性进行数值模拟研究，从压力分布图、流线分布图中详细地分析风圈式风量调节阀的流动特点，研究不同开度半径下阀门的阻力系数，研究阻力系数与阀门开度半径的函数关系，为工程应用和优化设计提供依据。

2 模型的建立和边界条件的设定

2.1 物理模型和边界条件

以DN200的风圈式风量调节阀为研究对象，按照1:1比例建立三维物理模型，计算区域长度为3600 mm，为了保证流场的稳定性，取阀门及前部管道L1=6D（D为管道直径），阀门及后部管道L2=12D。利用建模工具GAMBIT对其进行网格划分，为了保证网格质量和求解精度，对阀门附近区域处采用非结构化混合网格，并对阀门周围4D处的网格进行局部加密，而对进口4D及出口10D处管段采用结构化网格进行较为稀疏的网格划分，通过对物理模型进行多种不同网格划分，网格数量从稀疏到密集，验证网格独立无关性。最终，确定模型网格数约为60万，流动计算区域物理模型如图2所示。

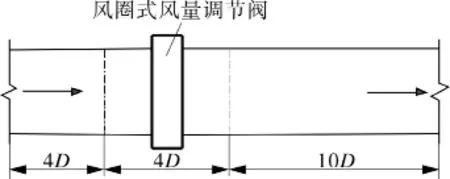
图2 物理模型

设置空气为流动介质，选择适用于工程问题的标准k-ε模型，对流项利用二阶迎风格式进行离散处理，离散方程的求解采用SIMPLE方法，收敛精度为10-4，近壁面采用标准壁面处理方式，忽略重力对流场的影响。入口边界设置为速度入口边界（velocity-inlet），选用入口速度为18 m/s，同时假设进口速度分布均匀。出口边界设置为自由出流（outflow）。

2.2 数学模型

流体流动控制方程[12,13]：

（1）不可压缩连续性方程

（2）不可压缩动量方程

（3）标准k-ε湍流模型

（4）k方程

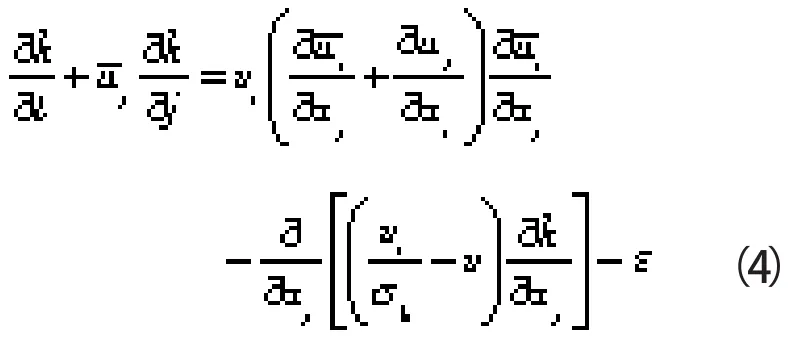
（5）ε方程

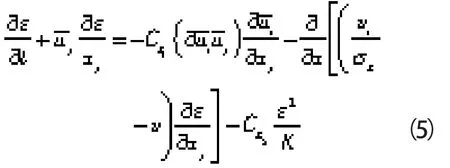
根据相关试验验证模型公式中的常数取值为Cμ=0.09，Cε1=1.44，Cε2=1.92，σk=1.0，σε=1.3。

3 模拟结果与分析

为了研究风圈式风量调节阀的流场特性，选取流场入口速度为2～20 m/s，对DN200、DN300、DN400、DN500的风圈式风量调节阀进行数值模拟研究，对DN200的阀门及入口速度为18m/s时的流场进行具体分析，由于阀门流体通道为圆形，开度即过流通道的半径R，对阀门不同开度下的模型进行了计算。并选取R=0.09 m、R=0.08 m、R=0.07 m、R=0.06 m、R=0.05 m、R=0.04 m、R=0.03 m 7组模型进行流动特性研究，现取其中4组进行具体分析。

图3 不同开度下阀门的压力云图

3.1 压力场分析

阀门前后两端压差大小对管道系统中的流体状态有着显著的影响，压强变化越缓慢，表明阀门在此时的性能越好，相反，若阀门前后压差急剧变化，将会对阀门及其后部管道产生较大的冲击，严重时将会损坏阀门及管道，为了得到阀门的流场特性，阻力特性规律，对于压力场的分析显得格外重要[14]。图3为不同开度下的阀门压力云图。

从图中可以看出，在开度R=0.09 m时，介质流过阀门时压力分布较为均匀，随着阀门开度R的减小，阀门前后压差依次增大，当开度较小时，如图3（d）所示，阀门前后的压差会急剧下降。对比图3中的4个云图，不难发现，不同开度R，阀门后部管道附近都会存在一个低压区，并且后续流场中压力逐渐趋于平稳。在阀门开度R=0.03 m时，阀门前后压差为极大，此时的阻力系数ζ高达294.78，因此，在实际工程中应该在合理的工作范围内使用该阀门，该阀门在开度R小于0.05 m时，不适宜工作。

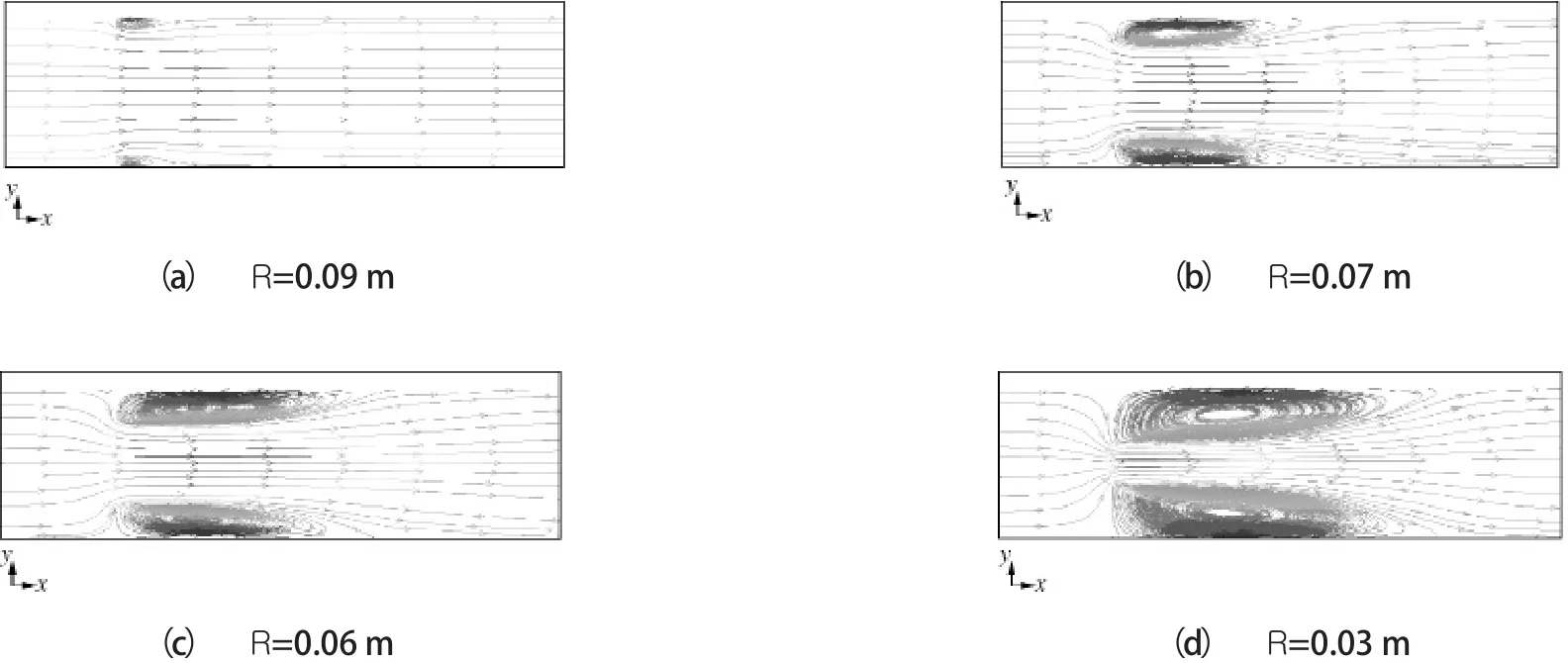
图4 不同开度下阀门的流线分布

3.2 流线分析

不同开度下阀门的流线分布如图4所示。从图4可见，不同开度下，围绕阀门下游管道会出现涡流区域，涡流区域中心压力最低，对流体的流动会产生扰动，流体的流态变的不平稳，这会造成不同程度的压力损失，造成系统能量损失。在开度较小的情况下，如图4（d）可见，流场内出现了大量的漩涡，流线紊乱，随着开度的减小，阀门下游管道涡流区域逐渐变大。当开度R=0.03 m时，涡流区域长度达2.5D。

4 阻力特性分析

阀门阻力系数计算式[15]：

根据计算得到阀门阻力系数ζ与阀门开度R及阀门过流截面积百分比的关系，见图5。

图5 阻力特性曲线

由图5可知，阻力系数与阀门开度呈指数关系，随着开度的减小，阻力系数呈指数增大趋势，在开度R小于0.05 m（开度截面积占25%）时，阻力系数变化明显，此开度下管道内流场紊乱，过快的启闭阀门对系统将形成极大的冲击；结合数值计算结果分析，当阀门开度小于0.05 m时，阀门前后压差较大，对阀门的弧形钢片及流场管道会有个极大的冲击力，同时对于管道流场的扰动也会加强，会造成大量的能量损失，因此，此时的阻力系数很大并且陡峭变化，结合表1和图5，不难发现，当开度大于0.05 m时，阀门阻力系数小并且曲线变化平缓，保持在一个较小的范围内。

通过对DN200，DN300，DN400，DN500的阀门及2～20m/s的入口速度设置边界条件并进行模拟，通过比较分析发现，阀门管径与入口速度对阻力系数的影响可忽略不计，阀门阻力系数与阀门开度有关，阀门开度不同将直接影响阀门的阻力系数，阻力系数与阀门开度都呈指数关系，对于本文研究的风圈式风量调节阀的阻力系数与阀门开度R存在如下函数关系：

以DN200风圈式风量调节阀为例，结合表1中的数据，通过拟合计算，得到DN200时的a=11794.35，b=-0.00811，c为修正系数，当阀门开度R小于0.05 m时c可忽略不计，当阀门开度R大于0.05 m时，c与阀门开度R有关，经过计算得到：

结合式（7）、（8）可计算出不同开度下的阀门阻力系数，经过数值计算与关系式计算结果对比分析，发现误差基本保持在5%之内，基本可以满足精度要求。

5 结论

（1）对DN200的阀门进行模拟计算，结果表明，当阀门开度小于0.05 m时，流场变得紊乱，阀门前后压强差及速度急剧增大；在不同开度下，阀门后部管道都会产生涡流，随着开度的减小，涡流区域逐渐变大，涡流区域中心压力最低。由于涡流的扰动作用，将会造成比较大的能量损失。

（2）对DN200的阀门阻力系数进行分析，结果表明，当开度R小于0.05 m时，阻力系数急剧增大，此时能量损失较大，不适宜阀门工作；当开度R大于0.05 m时，阻力系数小并且变化较为平缓；通过拟合计算，可以得到阻力系数与阀门开度函数关系式。（3）通过对多组不同管径、不同入口速度工况时的风圈式风量调节阀建立模型，对风圈式风量调节阀数值计算验证发现，阻力系数与阀门开度呈指数关系，并且阻力系数与阀门开度R都存在与式（7）相同的函数关系式。

（4）本文仅是通过数学建模后进行的数值计算分析，后续研究将开发风圈风量调节阀，在实验台上进一步进行对比试验。

［1］ 纪可.基于Fluent软件的大口径蝶阀流场研究［D］.沈阳：东北大学 , 2011.

［2］ 王海桥，陈永平，郝小礼，等.一种风圈式电动或气动风量调节阀［P］.中国,专利号：ZL201620697331.X，2016-07-05.

［3］ 何建慧,章永华.蝶阀内部流动特性仿真分析及结构优化［J］.机械研究与应用,2014，27(2):4-7.

［4］ 杨岩,杨恒虎,杨长辉,等.一种新型偏心蝶阀的 设 计 与 分 析［J］.流 体 机 械 ,2017,45(1)：48-54.

［5］ 宋学官 , 汪林 , 姜正浩 , 等 . 蝶阀流动特性的数值模拟及分析［J］. 流体机械 , 2008,36(5):25-29.

［6］ 崔宝玲,尚照辉,石柯,等.基于CFD的蝶板结构改进设计及数值分析［J］. 排灌机械工程学报,2013，31(6):523-527.

［7］ 官洪儿. 蝶阀与多板阀的内部流场数值模拟及结构静力分析［D］. 沈阳：东北大学 , 2010.

［8］ 何庆中 , 王渝皓 , 王佳 , 等 . 基于 CFX 的大口径蝶阀的流场分析及结构优化［J］. 流体机械 , 2016，44(5):42-46.

［9］ 诸葛伟林 , 刘光临 , 蒋劲 , 等 . 蝶阀三维分离流动的数值模拟研究［J］. 流体机械 , 2003,31(6):14-16.

［10］ 杨志贤 , 于娜 , 毛卫平 ,等 . 中心型蝶阀流场的数值模拟与流动特性分析［J］. 液压与气动,2016(1):95-99.

［11］ 张勤昭 , 刘福生 , 王宏 . 三偏心蝶阀的流场和阻力特性研究［J］. 流体机械 , 2013，41(11):1-5.

［12］ 韩占忠. FLUENT流体工程仿真计算实例与分析［M］. 北京 : 北京理工大学出版社 , 2009.

［13］ 王福军 . 计算流体力学［M］. 北京 : 清华大学出版社 , 2004.

［14］ 童成彪 . 蝶阀的优化设计和流场研究［D］. 长沙：湖南大学 , 2010.

［15］ 陆培文 . 实用阀门设计手册（第 3 版 )［M］. 北京 :机械工业出版社, 2012.