基于LES方法的壁面旋转旋流分离器内流特性的研究

徐 艳，张彦月，张井龙，闫月娟，王尊策

（1.东北石油大学，黑龙江大庆 163318；2.黑龙江省石油石化多相介质处理及污染防治重点实验室，黑龙江大庆 163318）

1 前言

旋流分离器具有体积小、结构简单及分离效率高等特点，其在应用于井下油水分离的过程中，常与螺杆泵配合使用，使壁面旋转，而壁面旋转旋流分离器流场的准确模拟存在困难。近几年采用LES方法模拟水力旋流器流场的研究越来越多，Slack等用LES方法模拟了旋风分离器，精确地预报了速度分布，同时得出：对于同一个几何模型，若采用LES方法模拟相对于雷诺应力模型需要更精密的网格［1］。De Souz和Silveira用LES方法模拟了76 mm的旋流管［2］。Delgadillo和Rajamani用LES方法模拟了Hsieh’s（1988）75mm的旋流管，研究表明LES模型虽然需要花费更大的计算费用［3］，但他们都得到了非常精确的速度分布，特别是对切向速度的预报尤为精确。

王尊策等采用标准Smagorinsky模型对28 mm Thew型旋流器内的单向流场进行了大涡模拟研究［4］，结果表明，大涡模拟在切向速度的预测较雷诺平均法有着明显的优势，但轴向速度预测精度较差。刘难生等采用大涡模拟方法，研究了绕轴旋转圆管内的湍流流动特性，与相应的直接模拟结果和试验数据进行了对比验证也得到了较好的效果［5］；崔桂香和许春晓等也通过直接模拟研究了旋转槽道湍流中旋转数对雷诺应力输运的影响［6］。而基于LES方法对壁面旋转旋流器内部流场的研究还比较缺少。

大涡模拟（LES）的基本思想是把湍流瞬时运动通过滤波函数分解成大尺度运动和小尺度运动。大尺度涡旋可以被计算网格分辨，其运动通过Navier-Stokes方程直接计算，小尺度涡尺度量级上小于网格，无法被网格分辨，通过引入亚格子尺度应力（SGS）模型来模化小尺度涡旋的运动［7～14］。本文以井下用28mm Thew型旋流器为例，基于大涡模拟方法对其绕轴旋转旋流器内部流流场进行数值模拟，通过分析不同转速情况下，各截面上的切向速度、轴向速度的分布情况，以期得到更为准确的流场分布规律。

2 数值方法与物理模型

2.1 大涡模拟方法

2.1.1 控制方程

滤波后的Navier-Stokes方程如下：

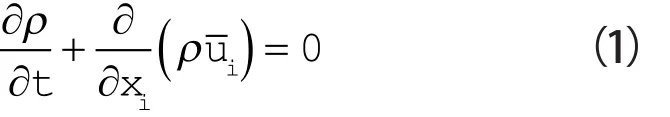
式中 ρ——流体密度

υ——流体运动黏度

根据Boussinesq假设，SGS应力计算式：

其中

2.1.2 亚格子模型

本文采用Kim和Menon等在1997年提出的湍动能输运亚格子模型（KET）［15］，它在非均衡湍流的复杂流动中应用效果良好［16］。

亚格子尺度动能计算式：

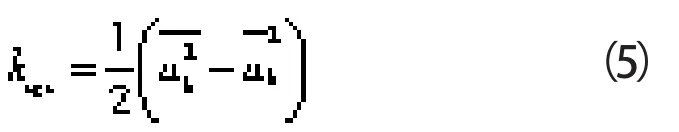
V——计算单元体积

所以，亚格子尺度应力为：

式中，2Ck和由动态属性决定，固定设为1.0。

2.2 物理模型

旋流器采用Thew提出的双锥旋流分离器结构，由2个切向入口、旋流腔、大锥段、小锥段、尾管、底流出口和溢流出口组成，D=56 mm，具体结构见图1。工作时液体由两侧切向入口流入，在旋流器内部形成强螺旋流，分离后的液体分别从底流和溢流流出，同时壁面绕轴心做旋转运动。

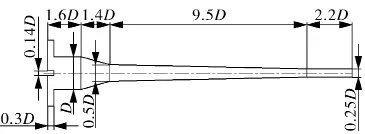
图1 绕轴旋转旋流器结构示意

2.3 网格与计算条件

2.3.1 网格划分

采用ICEM CFD作为网格划分工具，为保证LES对黏性底层求解要求，把第一层网格中心布置在黏性底层，整个计算域的网格为结构的六面体网格，网格总数为4.0×106，近壁面区网格基本满足y+=O（1），保证了计算中对流场小尺度涡的精确捕捉，其网格见图2。

图2 网格划分条件及初始条件

2.3.2 边界

入口为速度入口，入口流速为0.5 m/s，水力直径为16.6 mm；底流和溢流为自由出流，分流比分别为95%和5%；壁面采用无滑移壁面边界条件，设定壁面旋转速度。

2.3.3 控制方法

控制方程在空间上采用有限体积法进行离散，由柯朗数近似等于1，计算得到时间步长为0.005s，具体数值计算方法见表1。

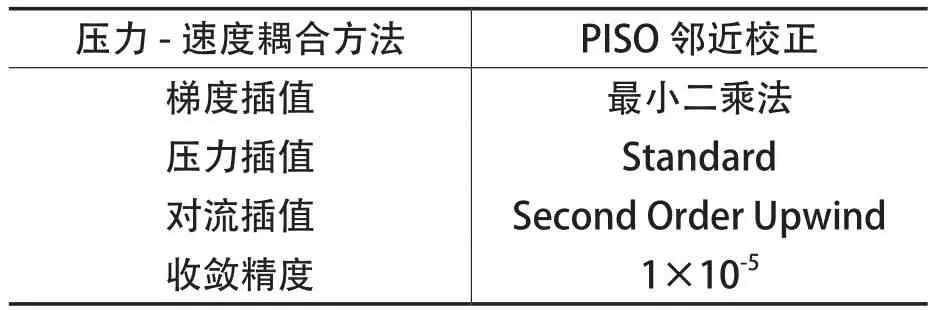
表1 离散格式与精度

3 计算方法验证

3.1 LDV测速试验

按照数值模拟所用旋流分离器的结构，1∶1比例建立流场测试工装，采用清华大学SCD-23型频移激光测速系统，对其内流场进行LDV测试。该流程由供液罐、动力泵、流量计量、压力计量、控制阀、旋流分离器、激光测速装置等组成。激光测试系统如图3所示。试验测试入口速度0.5 m/s条件下，旋流器Z=150 mm、Z=200 mm和Z=300 mm 3个截面位置的流体切向速度。

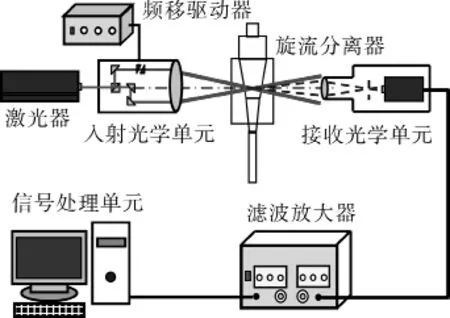
图3 激光多普勒测速系统示意

3.2 试验结果与数值计算结果的对比与分析

图4 中对比了壁面转速分别为0，300 r/min时不同截面上的切向速度分布。

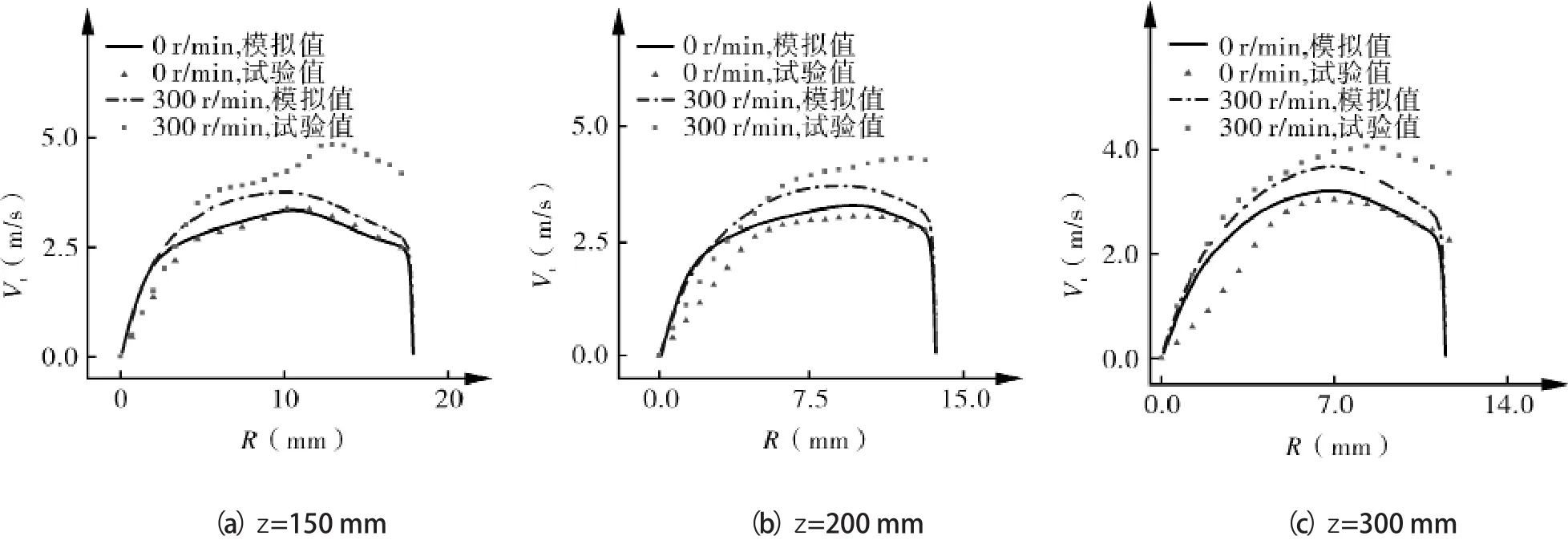
图4 切向速度对比

从图可以看出，当壁面转速为0时，模拟结果与试验结果吻合较好，当壁面转速为300 r/min时，模拟结果在轴心位置与实测结果吻合较好，在近壁区存在一定的变差，但在整体趋势基本一致，故选用的模拟方法可靠，可以从定性上描述出旋转壁面旋流分离器的流场分布规律。

4 数值模拟结果分析

由于旋流器在不同轴向位置呈现不同的变化规律，因此取z=150 mm，z=200 mm，z=300 mm位置考察速度分布。

4.1 切向速度分布

在不同壁面转速（-500，-300，0，300 和 500 r/min）情况各截面的切向速度分布如图5所示。

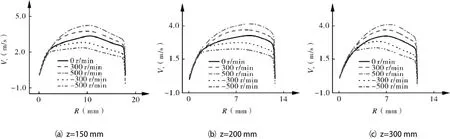
图5 不同转速下各截面切向速度分布

由图中可以看出，旋转壁面旋流器切向速度的分布与传统静态旋流器的整体分布趋势一致，速度场呈现出典型的双涡结构，内部为类似于满足刚体旋转的准强制涡，外部为准自由涡。切向速度整体上从边界开始随半径的减小逐渐增大，并存在一个最大的切向速度点，从最大的切向速度点开始，半径进一步减小时，切向速度逐渐减小，直至中心点处切向速度接近于零。比较不同转速对切向速度分布的影响可以看出，正转时，随着壁面转速的增加，外涡流区的切向速度随之增加，但增加量不随半径的减小而减小，内涡流区的切向速度增加不明显，最大切向速度点有向壁面移动的趋势，外涡流区的范围减小。反转时，影响趋势则正好相反，即随着壁面转速的增加，外涡流区的切向速度随之减小，内涡流区的切向速度减小的不明显，最大切线速度点内移，外涡流区的范围增大。反转时切向速度的减小量要大于正转时切向速度的增加量。从不同轴向位置截面的切向速度对比来看，最大切向速度值没有明显的变化。

4.2 轴向速度分布

在不同壁面转速（-500，-300，0，300 和 500 r/min）情况下各截面的轴向速度分布如图6所示。

图6 不同转速下各截面轴向速度分布

由图中可以看出，壁面旋转效应对不同轴向位置截面的影响并不相同，轴向速度有较明显的差异，正向旋转时轴向速度的分布与静止壁面旋流分离器的整体分布趋势相似。z=150 mm时，正转时，随着转速的增加，内涡流区轴向速度逐渐降低，向底流流动趋势减弱，外涡流区轴向速度逐渐增加，向底流流动趋势增强，中间存在过渡区域；反转时，内涡流区轴向速度明显减小；随着壁面转速的增加，向底流流动趋势减弱，在500 r/min时出现了负值，即流体出现回流，向溢流口流动；为了维持截面上流量的平衡，外涡流区，向底流流动趋势增加，内外涡流过渡区域轴向速度低于静止壁面。z=200 mm时，轴向速度的分布发生了变化，但壁面旋转对轴向流场产生的影响规律与z=150 mm有类似，近壁区反转时的轴向速度低于静止壁面，过渡区高于静止壁面。z=300 mm时，正转时，轴向速度的分布规律与静止壁面相似，但整体向壁面偏移，引起内涡流区速度增加，外涡流区速度减小；反转时，轴向速度整体向左偏移，内涡流区轴向速度仍然延续上面2个截面的分布规律，但没有出现负值；近壁区分布与z=200 mm时类似。

5 结论

（1）基于KET大涡模型，压力-速度耦合采用PISO邻近校正，梯度差值采用最小二乘法，压力差值采用Standard格式，对流差值采用Second Order Upwind，建立了旋转壁面旋流分离器数值计算模型，并通过LDV测试结果验证了模型的可靠性。

（2）对壁面旋转旋流分离器内流场进行LES模拟，正转时，外涡流区的切向速度逐渐增加，增加量基本不随半径的减小而衰减，内涡流区切向速度增加不明显，反转时，影响趋势则正好相反，但反转的切向速度减小量大于正转时切向速度的增加量。增大了轴向速度的变化梯度；反转时，则正好相反。

（3）壁面旋转效应对不同轴向位置截面的影响并不相同，轴向速度有较明显的差异。正转时，轴向速度的分布与静止壁面旋流器的整体分布趋势相似，整体有向右偏移趋势；反转时，内涡流区轴向速度明显减小，在转速为500 r/min出现了回流现象。

［1］ Slack M D，Prasad R O，Bakker A，et al.Advance in cyclone modeling using unstructured grids［J］.Transactions of the Institution of Chemical Egineers，2000，78（A11）：1098-1104.

［2］ De Souza J，Silveira A.Preliminary results of large eddy simulations of a hydrocyclone［J］.Therm.Eng，2004，3（2）：168-173.

［3］ Delgadillo J A，Rajamani R K.A comparative study of three turbulence-closure models for the hydrocyclone problem［J］.Int.J.Miner.Process，2005，77（4）：217-230.

［4］ 张井龙，王尊策，吴卓，等.液-液旋流分离器内流动特性的大涡模拟［J］.化工机械，2013（3）：335-339.

［5］ 刘难生，仲峰泉，陆夕云，等.旋转圆管湍流的大涡模拟数值研究［J］.力学学报，2002（6）：833-846.

［6］ 杨子轩，崔桂香，许春晓，等.旋转槽道中Taylor-Gortler涡对雷诺应力输运方程的影响［J］.中国科学：物理学 力学 天文学，2010（6）：781-790.

［7］ 王福军.计算流体动力学分析：CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［8］ 张兆顺，崔桂香，许春晓.湍流大涡模拟的理论和应用［M］.北京：清华大学出社，2008.

［9］ 刘杨，王振波.水力旋流器分离效率影响因素的研究进展［J］.流体机械，2016，44（2）：39-42.

［10］ 赵宇，赵立新，徐保蕊，等.基于正交法的一体化二次分离旋流器结构参数优选［J］.流体机械，2016，44（3）：29-33.

［11］ 刘丽艳，冯家祥，吴皓，等.换热器管束排列角对流体力的影响研究［J］.压力容器，2016，33（12）：13-19.

［12］ Cui G，Zhou H，Zhang Z，et al.A new dynamic subgrid eddy viscosity model with application to turbulent channel flow［J］.Phys Fluids，2004，16（8）：2835-2842.

［13］ Lee Y.A study and improvement of large eddy simulation for practical applications［D］.Ph.D dissertation，Texas A&M University，USA，1992.

［14］ 王春林，司艳雷，赵佰通,等.旋流自吸泵内部湍流场大涡模拟［J］.农业机械学报，2009（9）：68-72.

［15］ Kim W，Menon S.Application of the localized dynamic subgrid-scale model to turbulent wall-bounded flows［R］.Technical Report AIAA-97-0210.35th Aerospace Sciences Meeting，Reno，NVAmerican Institute of Aeronautics and Astronautics.January 1997.

［16］ 周磊，解茂昭，贾明.不同亚网格尺度应力模型在燃油喷雾大涡模拟中的应用［J］.内燃机学报，2011，29（1）：30-32.