涡轮增压压气机叶轮的气动优化设计

叶 涛，陈 飞

（武汉理工大学，湖北 武汉 430070）

1 前言

随着节能环保要求的日益增高，涡轮增压器越来越广泛地使用在汽车上。对于相同排量的发动机，采用涡轮增压可显著提高发动机的功率和扭矩，提高燃油利用率，降低排放。压气机作为涡轮增压器的核心部件，其性能的好坏对增压效果有重要影响。近年来，汽车向小排量发展，这对压气机气动性能提出了更高的要求。对压气机进行气动优化，进而设计出高效率高压比的满足实际需要的压气机成为研究学者研究的一个方向。

近年来，随着计算机技术和计算流体力学的发展，数值模拟广泛应用于压气机的气动优化设计中。Xiaomin Liu等采用响应面法和多目标遗传算法分别对离心压气机进行优化，优化后压气机的绝热效率分别提高1.0%和3.0%，结果表明在对压气机进行优化时，多目标遗传算法优于响应面法［1］。Hildebrandt等利用多目标优化法，分别对离心压气机弯道和回流器叶片进行优化，优化后，损失系数减小［2］。冀春俊等对某型压气机进行优化，优化后压气机的内部流场得到很大改善，压气机整机效率提高4.09%，而且在设计转速下的稳定工作范围得到提高［3］。刘波等采用人工神经网络结合遗传算法对带有分流叶片的离心压气机进行优化，优化后设计点等熵效率提高3.68%，压比提高0.506%，综合稳定裕度增大，流动损失减少［4］。陶胜等提出在三维环境下进行二维叶型优化设计，通过改进能量方程中的粘性耗散项形成新的流场计算模块，并结合并行遗传算法寻优模块，分别对离心叶轮和斜流叶轮进行优化设计，优化后的叶轮效率明显提高［5］。

本研究以某型小型压气机为对象，采用逆向工程技术中的三维扫描的方法反求压气机叶轮，建立叶轮的几何模型，在此基础上，利用参数化拟合对叶轮进行参数化建模，进而利用人工神经网络和遗传算法对叶轮进行气动优化设计。

2 几何模型的建立

目前采用逆向工程技术对叶轮进行测量建模主要包括接触式和非接触式，前者使用三坐标测量机，后者使用三维扫描仪［6～13］。本研究采用三维扫描仪对压气机叶轮进行扫描，获取叶轮的点云数据。所研究的叶轮的基本数据如表1所示。采用精度为0.01 mm的扫描仪，对叶轮进行扫描，在扫描获取叶轮点云数据之后，采用点云后处理软件Geomagic Studio对叶轮的点云数据进行前期处理，包括去除偏离主点云的数据点，删除体外孤点，通过压缩点云数据带减少噪声点，通过统一采样去除重叠点，减少点云的数量。在对点云进行前期处理后，采用imageware软件分别对叶轮模型的轮毂、轮缘、吸力面和压力面进行重构，然后在pro/E中对模型进行组合，最终建立的三维模型如图1所示。

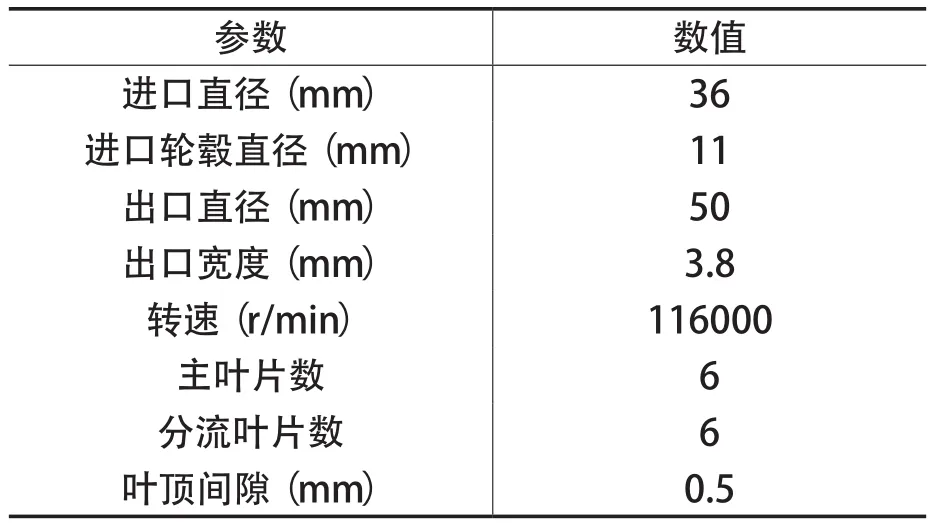
表1 叶轮的基本数据

图1 叶轮的三维模型

3 原模型的数值模拟

采用NUMECA公司的Fine/Turbo软件包对叶轮进行流场计算，得出流场的计算结果，为进一步对叶轮进行气动优化作准备。

具体过程为：（1）生成几何文件：将反求获得的几何模型导入到IGG模块中，并提取所需的几何型线和面，然后根据所提取的几何数据在AutoGrid4模块中生成最终所需的*.geomTurbo几何文件。（2）网格的划分：采用自动结构化网格模块AutoGrid5对叶轮进行网格划分，采取O4H网格拓扑，叶片采用蝶型网格，壁面第一层网格宽度为3×10-5m，网格总数为138.8万，最小正交角为16.4°，划分好的网格如图2所示。（3）数值计算：控制方程为湍流纳维-斯托克斯方程，湍流模型为S-A模型，采用轴向进气，进口压力为99.1 kPa，进口温度为298 K，出口给定平均静压，计算转速为116000 r/min，采用二阶中心差分格式进行空间离散，四阶龙格-库塔进行时间离散，同时采用多重网格技术和隐式残差法加速收敛。

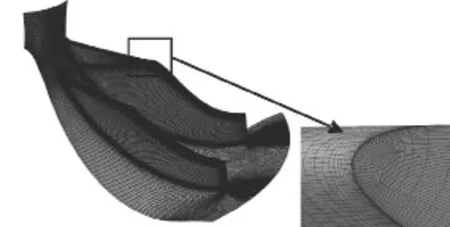
图2 网格

4 叶轮的优化

采用Fine/Design3D优化平台对叶轮进行气动优化，其基本优化思想是应用原始叶型所获得的知识库来加速新叶型的设计。该平台主要的优化方法是采用人工神经网络（ANN）结合遗传算法的方法，优化的精度取决于神经网络的知识库，优化的目的是要找到使用简化分析模型的目标函数的最小值。Fine/Design3D软件主要由模拟向导模块CFD_Screending、数据库生成和管理模块Database_Generation和优化模块Optimization三个模块组成。叶轮的优化流程如图3所示。

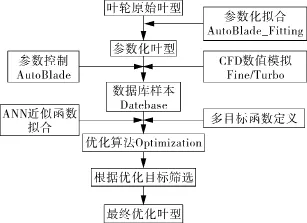
图3 叶轮的优化流程

4.1 叶型参数化

叶轮进行优化前，需要对叶型进行参数化拟合，基本要求就是用一系列多项式曲线准确描述叶轮的叶型数据。此过程在AutoBlade_Fitting模块中完成。轮毂线和轮缘线采用B样条曲线进行参数化拟合，控制点数均为8个。

三维叶片是根据叶高方向上各截面叶型按指定的积叠方式积叠而成。本文所研究的叶轮的积叠点选为叶型前缘点，积叠线采用直线。叶型型线采用中弧线加厚度分布的方式定义，叶型厚度沿中弧线对称分布，中弧线采用B样条曲线拟合，控制点为4个，叶型型线采用Bezier曲线拟合，控制点为3个，前缘采用圆头，后缘采用钝头处理，叶型参数化方法如图4所示。

图4 叶型参数化方法

参数化拟合时，先进行粗拟合，根据拟合结果调整部分参数的值，再进行精确拟合，通过多次拟合提高叶型拟合的精度。拟合时，叶轮各型线所对应的拟合参数个数如表2所示。

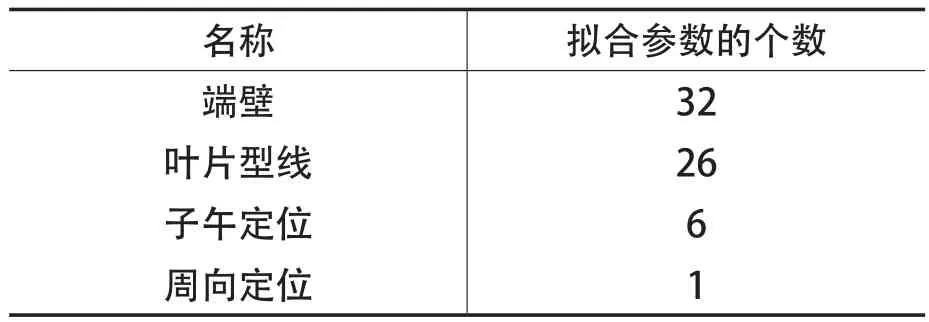
表2 拟合参数

4.2 优化

在流量为0.09 kg/s工况下，对叶轮进行优化，以效率和压比为优化目标。为了实现优化目标，需将约束项转化为罚函数项。由罚函数构造的目标函数为：

式中 W1——质量流量

W2——压比

W3——等熵效率的加权因子

Qimp——质量流量给定值

Qref——质量流量参考值

Q——质量流量计算值

πimp，πref——给定压比、参考压比

π，η——压比、效率计算值

Design3D优化是基于近似函数方法以及优化算法展开的，因此在优化之前需要为优化过程提供有限数量的样本，样本数要足够多，以覆盖优化参数的整个变化范围，保证得到全局最优解，同时样本数要尽量少，以减小计算量，本次优化用于人工神经网络学习的样本数为30个。优化算法为遗传算法，初始种群设定为50，遗传代数为80，迭代次数为40。

5 优化结果分析

优化后，在优化点，叶轮等熵效率为87.13%，总压压比为1.84，效率比原模型提高了2.01%，压比比原模型提高了0.12。优化前后叶轮的流量-效率，流量-压比特性曲线如图5如示。从图可见，优化后，叶轮的效率和压比都得到提高，综合稳定裕度也提高了。

图5 特性曲线

5.1 几何型线对比分析

图6 叶片截面几何型线对比

优化前后叶片截面几何型线如图6所示，从图可见，优化后的叶型与原叶型的形状基本相同，但是在叶根处，优化后叶片前缘叶片角略微增大，尾缘叶片角有所减小，叶片型线增体向尾缘偏移，叶片弦长保持不变；在叶尖处，主叶片基本与原叶片一致，而分流叶片叶型变化较大，叶型分别向前缘尾缘延伸，叶片弦长有所增加。

5.2 流场结果对比分析

以上流场计算结果已经显示优化后叶轮的效率和压比都比原叶轮高。为了进一步研究影响叶轮效率和压比的原因，本文将主要对比分析叶轮内部流场的压力，叶轮叶片前缘、尾缘以及叶尖等部位的流动状况。图7为主叶片和分流叶片在10%、50%和90%叶高处叶片表面的静压。

图7 10%，5%，90%叶高处叶片表面静压

从图可见，叶片表面压力沿弧长逐渐增加，且优化后叶片表面压力得到提高。由于叶片压力升高，叶轮出口压力也相应增大，因此叶轮的压比得到提高。在90%叶高处，叶片表面静压分布不均，出现波动，这一现象在主叶片上表现得更为明显。这是因为90%叶高处靠近叶尖，受叶尖泄漏涡的冲击，叶片表面压力出现波动。

图8为在优化前后叶片前缘的压力沿展向的分布情况。从图可见，分流叶片前缘压力大于主叶片前缘压力；优化前，主叶片和分流叶片前缘压力分布不均，波动幅度大，优化后前缘压力分布均匀。这是因为优化后叶片前缘叶片角得到调整，从而获得合理的气流冲角，使压力分布均匀，减少冲击损失。在靠近叶尖处，优化前后，主叶片和分流叶片的前缘压力都急剧下降，这是因为叶尖存在泄漏。

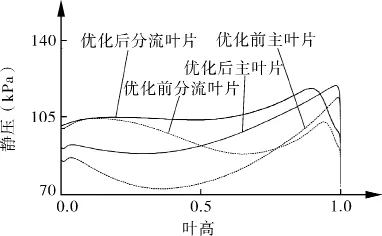
图8 前缘静压沿展向分布

图9 为叶轮出口处S3流面的相对马赫数。

图9 叶轮出口处S3流面的相对马赫数

图中结果显示：在图的左上角，也就是叶片吸力面侧靠近轮缘附近，有一个明显的低马赫数区，这是由于叶尖泄漏气流冲击主流道气流，形成局部漩涡，这些漩涡会导致气流滞留，引起流道阻塞，造成能量损失，影响压力机的效率和压比。优化后，低马赫数区的马赫数得到提高，最小马赫数从0.118提高到0.2，阻塞现象得到改善，气流能量损失减小。

6 结论

（1）采用B样条曲线和Bezier曲线实现了对叶轮端壁和叶片的参数化拟合，用最少的控制点实现了对轮毂、轮缘和叶片的建模与控制，且拟合精度高。

（2）利用人工神经网络和遗传算法实现了对叶轮的优化。优化后，叶轮的气动性能得到很大提高，在优化点叶轮的效率比原模型提高了2.01%，压比比原模型提高了0.12，综合稳定裕度也提高了。

（3）对比分析优化前后的计算结果，得出：优化后，叶片前缘叶片角增大，尾缘叶片角减小，叶片载荷提高了，叶片前缘的压力分布变得均匀了，叶轮出口处的流动得到改善，流动损失减小。

［1］ Xiaomin Liu, Wenbin Zhang. Two Schemes of Multiobjective Aerodynamic Optimization for Centrifugal Impeller Using Response Surface Modal and Genetic Algorithm［R］. ASME 2010-GT-50262.

［2］ Hildebrandt A. Aerodynamic Optimization of a Centrifugal Compressor Return Channel and U-turn with Genetic Algorithms［R］. ASME 2011-GT-50262.

［3］ 冀春俊,李晓庆,余道刚.增压器压气机流动分析与全工况优化［J］.流体机械 ,2012,40（1）:26-30+21.

［4］ 刘波,杨晰琼,曹志远,等.带分流叶片离心压气机优化设计［J］.推进技术 ,2014,35（11）:1461-1468.

［5］ 陶胜,周正贵,严欣,等.三维环境下离心/斜流压气机二维叶型优化设计［J］. 航空动力报,2014（12）:2965-2972.

［6］ 黄国权,杨显惠. 采用逆向工程技术对叶轮建模的研究［J］. 机械设计与制造 ,2010（2）:227-229.

［7］ 张伟,赖喜德,宋威,等.基于激光扫描的离心泵闭式叶轮反求技术［J］.热能动力工程,2014,29（5）:539-543.

［8］ 刘力歌，冯文卓，高欢，等.一种新型网壳储罐的支座结构及其优化［J］.压力容器，2016，33（2）：30-74.

［9］ 李强，王磊，马国顺，等.核电站主蒸汽超级管道热挤压管设计优化［J］.压力容器，2015，32（8）：40-43.

［10］ 王天宇，王霄，刘会霞，等.发动机冷却风扇性能的优化设计研究［J］.机电工程，2015，32（6）：744-749.

［11］ 何立博，姜涛，李志锋，等.多翼离心风机叶轮的正交设计与试验分析［J］.流体机械，2016，44（9）：7-11.

［12］ 刘希昌，莫秋云，李帅，等.小型垂直轴风力发电机的气动噪声数值模拟与试验验证［J］.流体机械，2016，44（6）：11-16.

［13］ 潘为民,叶欣,孔宁宁,等.基于三坐标测量机的精密叶轮测量路径规划研究［J］. 机床与液压,2016,44（7）:14-17.