基于改进ELM的撑杆跳起跳过杆轨迹模型研究

，，，

(浙江理工大学，a.信息学院；b.体育部，杭州 310018)

0 引 言

在撑杆跳高运动中，起跳、团身、过杆是几个比较重要的基础技术[1]。要想成功越过横杆，运动员必须通过助跑起跳获得一定的动能，在团身阶段完成空中动作以致过杆。我国撑杆跳高运动成绩目前提高较快，但整体水平一直落后于世界，在亚洲的成绩排名也不理想。所以提升起跳、团身、过杆技术成为了提高撑杆跳高成绩非常重要的方面。

Fukushima等[2]利用撑杆跳高机器人，论证了在杆上更积极主动地团身，能改善撑杆跳高成绩。Liu等[3]提出了通过动力学优化控制模型，结合测量的相关参数，来对撑杆跳高运动员的表现做分析，发现握杆高度、起跳角度以及撑杆的柔性度与撑杆跳高成绩的关系。Nishikawa等[4]利用机器人论证了撑杆跳高过程中恰当的摆体时机能提高撑杆跳高的运动成绩。李北玉[5]通过分析文献资料，指出决定撑杆跳高成绩的主要因素有运动员握杆的高度、起跳时的速度和腾起的高度。上述对撑杆跳高的研究要么只考虑了运动的某一个环节，忽略了其他环节间的相互影响和人体在杆上具体的动作形态；要么只是根据数理统计方法得出影响运动成绩的因素，而没有给出帮助运动员提升日常训练的手段。针对上述问题，本文在分析了原始极限学习机(Extreme learning machine，ELM)隐层节点参数选择方法的基础上，通过正则化理论以及差分进化算法(Differential evolution algorithm，DE)对ELM进行参数寻优，提出了DE-RELM起跳过杆模型。该模型充分考虑了运动员起跳、团身、过杆三个环节，并提取相应特征作为此次起跳过杆轨迹的特征，以此来判定过杆成功与否。同时对过杆成功与失败时提取的特征进行对比分析，以帮助运动员提升日常训练，实现对起跳过杆过程的指导。

1 起跳过杆模型算法原理

1.1 ELM算法原理

由Huang等[6-7]提出的ELM算法，是一种快速的单隐层神经网络训练算法，可用于进行分类和回归预测分析[8]。它的特点是在网络参数训练过程中，隐层参数随机选取，外权的求解化归成求解一个矩阵的Moore-Penrose广义逆问题。

ELM算法的网络结构如图1所示，可以看出，它是一个简单的SLFN(单隐藏层前馈神经网络)。

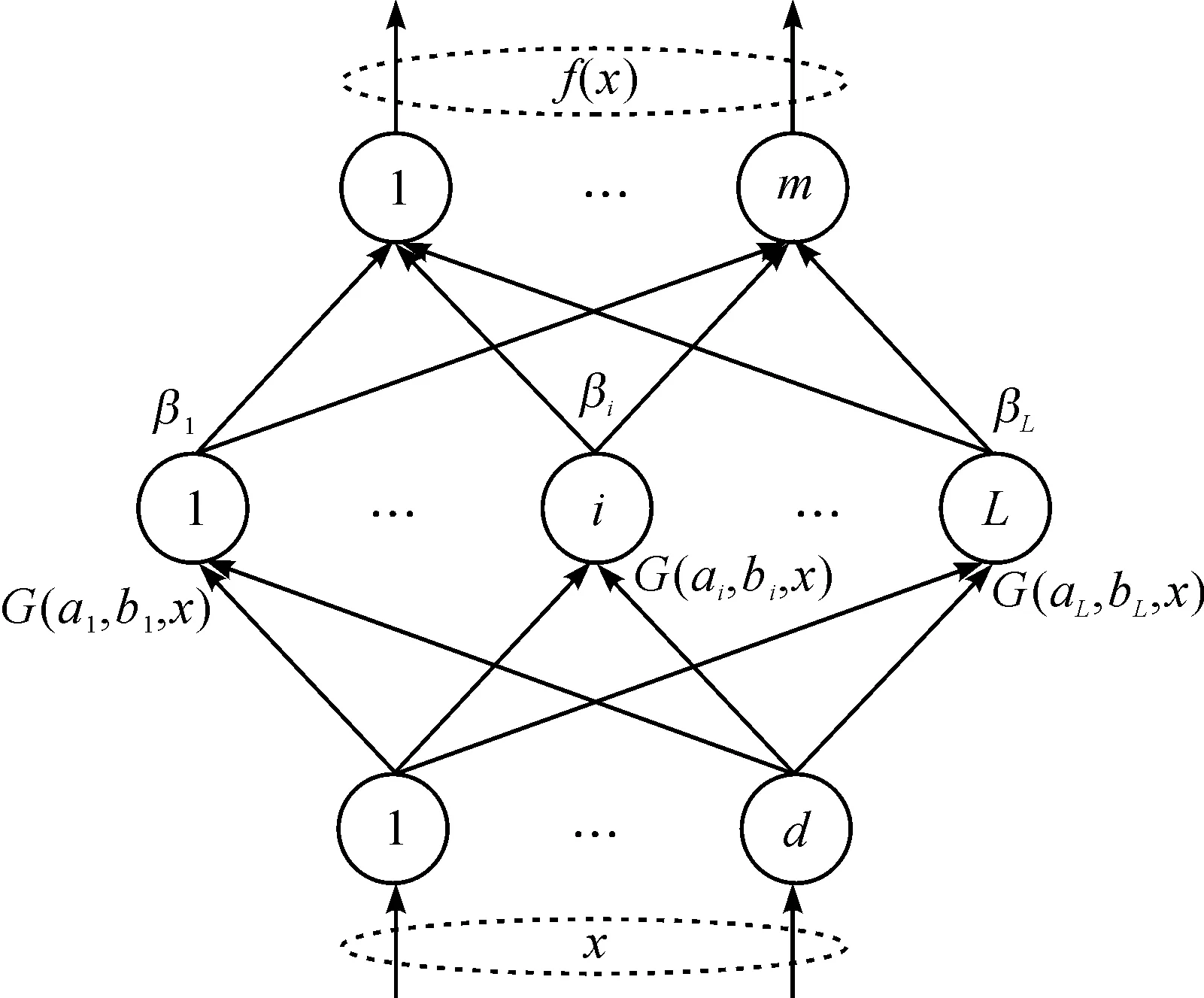
图1 ELM网络结构

图1中ai和bi为隐层节点参数，βi表示第i个隐层节点和网络输出之间的连接权值向量，G(ai，bi，x)表示第i个隐层节点对应于样本x的隐层节点输出，隐层节点的激活函数可以是RBF、Sigmoid或Sine函数等。对于具有L个隐层节点的单隐层神经网络的输出表达式如式(1)所示：

(1)

式(1)可以简记为式(2)：

Hβ=T

(2)

其中H如式(3)所示：

H(a1，…，aL，b1，…，bL，x1，…，xN)=

(3)

β和T分别如式(4)和式(5)所示：

(4)

(5)

设代价函数E(W)表示网络输出和样本的实际值间的误差平方和，所以问题求解就是寻找最优全值W=(a，b，β)使E(W)最小，其数学模型如式(6)所示：

(6)

其中ej是第j个样本的实际值和网络输出间的误差。

1.2 正则化的ELM

由统计学理论可知，实际风险应当由经验风险和置信范围两部分组成[9]。虽然ELM泛化能力强，但其只考虑了经验风险，没有考虑置信范围，可能会导致过拟合问题，所以本文把结构风险最小化理论引入到ELM中，提出正则化的ELM(Regularized ELM，RELM)。通过参数λ来调节两种风险的比例，并取得最佳的折中。RELM数学模型如式(7)所示：

(7)

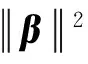
(8)

其中α=[α1，…，αN]，表示拉格朗日乘子。

1.3 差分进化算法原理

差分进化算法(Differential evolution algorithm， DE)[10]是一种高效的基于种群迭代的群智能优化算法。该算法作为一种新的进化计算技术，具有结构简单、待定参数少、不易陷入局部最优、收敛速度快等优点，在智能计算领域成为了一个研究热点。DE算法的具体操作如下：

a) 初始化。NP个个体组成的初始种群xi(0)，维数为D，xi(0)可随机生成，如式(9)所示：

j=1，2，…，D}

(9)

其中xj，i(0)如式(10)所示：

(10)

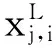
b) 变异。变异操作在差异演化中十分重要，是从种群中随机选择3个个体：xk1、xk2和xk3，且k1≠k2≠k3≠i，则变异操作如式(11)所示：

vi(g+1)=xk1(g)+F·(xk2(g)-xk3(g))

(11)

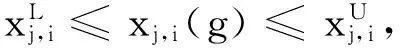
c) 交叉。为了添加种群的多样性，进行交叉操作，如式(12)所示：

(12)

其中CR∈[0，1]为交叉概率，jrand为[1，2，…，D]上的随机数。

d) 选择。为选择进入下一代种群的个体，DE算法用适应度函数f对向量ui(g+1)和xi(g)进行比较来生成g+1代种群，如式(13)所示：

(13)

e)g=g+1。反复执行步骤b)到步骤e)，直到满足所要求的收敛精度或达到最大的进化代数。

1.4 改进的RELM

虽然RELM考虑了结构风险，且在网络参数的确定过程中，隐节点的参数是随机选取的，可以提高算法的学习速度，但相对于输入数据而言这些参数并不是最优的选择，精度也有待提高。在实际应用中，为使得ELM有较好的性能，往往会增加隐层节点的个数，这样做会带来过拟合的风险，同时也会增加算法的复杂性。为提高算法的精度，减少隐层的节点数，本文利用差分进化算法的全局寻优能力，为正则化的极限学习机寻找合适的网络参数，并将其作为训练DE算法的适应度指标，以获得最佳网络。最后将优化的ELM应用到数据的分类处理当中[11-12]。

利用差分进化优化的正则化极限学习机(DE-RELM)流程如图2所示，基本步骤如下：

给定一个训练样本集S={(xi，ti)|xi∈Rn，ti∈Rm，i=1，2，…，N}，激励函数g(x)，最大迭代次数Gmax以及隐层节点的个数k。其中，每个样本表示一次起跳过杆的特征向量和是否成功过杆。

a) 采用经验值估计法初始化参数NP、F、CR，并随机生成一组初始种群QNP×D，每种种群Q(t)={a11，a12，…，a1l，a21，a22，…，a2l，…，an1，an2，…，anl，b1，b2，…，bl}。

b)对于每个种群，计算隐层输出矩阵得到输出权值，并求出其相应的均方根误差作为适应度指标，具体如式(14)所示：

(14)

c)种群中的个体根据DE算法，先进行变异得到个体Vi(g+1)，再进行交叉获得新个体Ui(g+1)，然后选取有竞争力的个体进入下一代种群的个体，选取过程如式(15)所示：

(15)

其中，J(•)代表其适应度指标。

d)根据迭代次数判断程序是否继续进行。若在迭代次数范围内则重复步骤b)和步骤c)，直至目标完成，否则直接进入步骤e)。

e) 输出权值β。

f) 程序结束。

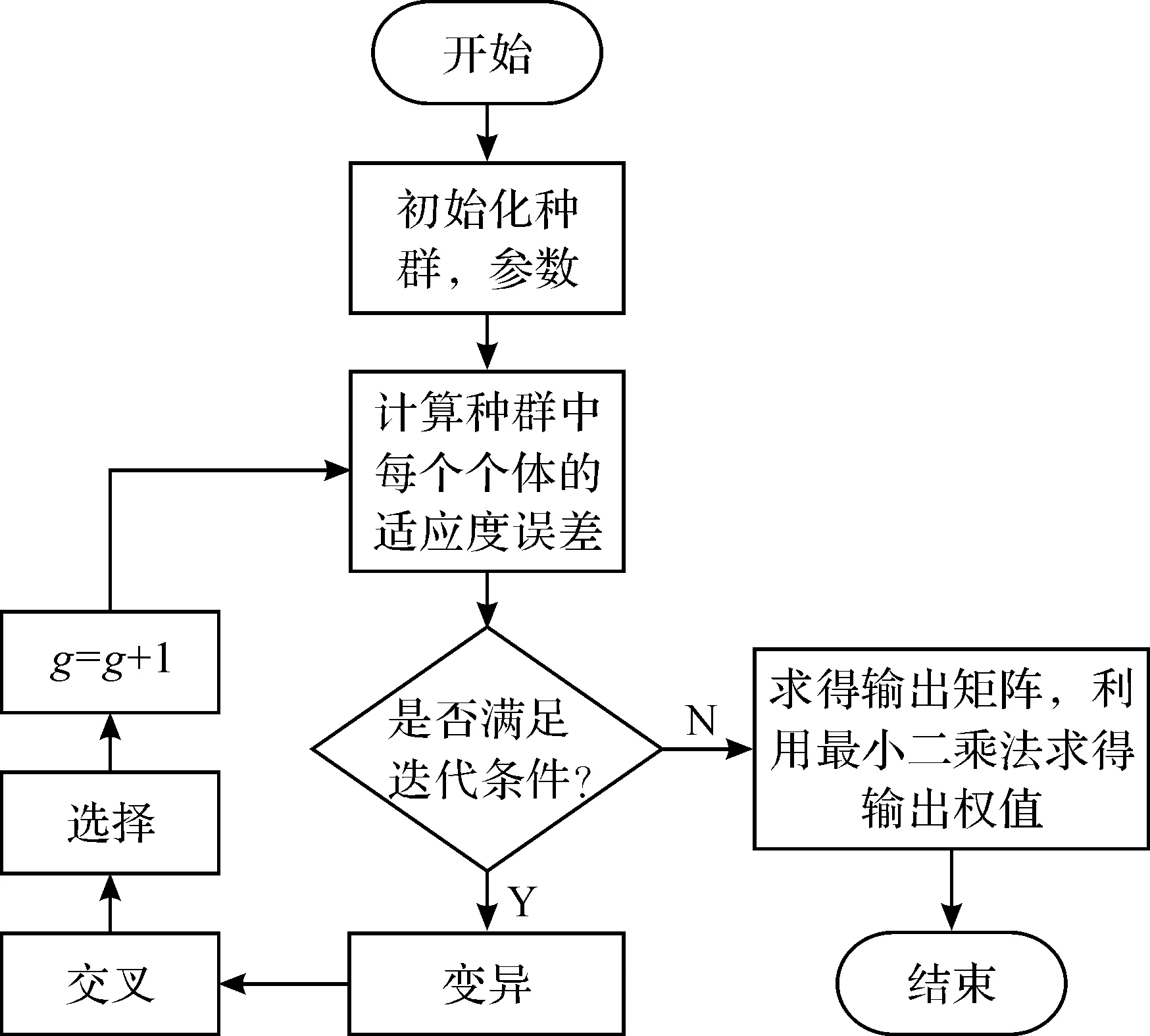
图2 DE-RELM算法流程

2 仿真实验和分析

2.1 三维红外运动捕捉系统

OptiTrack三维红外运动捕捉系统通过在人体或其他物体上布置标记点，由高速相机接受标记点反射的红外光，然后识别标记点来认知人体，从而实时捕获人体的运动姿态和在空间坐标系中位置信息。图3(a)为附着标记点的人体。

图3 带有标记点的人体

本文使用的高速相机为12台Prime13(简称p13)，其最高帧速为240 fps，分辨率达到1280*1024，视场角为56°，处理延迟为4.2 ms，最远工作距离为14 m。为了避免标记点越出高速相机的捕捉范围，导致检测数据可能出现的空白，应尽可能扩大捕捉范围，防止出现错误。

2.2 实验数据采集

本实验的研究对象是撑杆跳过程中的起跳过杆，即起跳、团身、过杆，这是撑杆跳运动中三个重要的阶段。实验要求运动员在保证最大过杆率的情况下，尽可能越过高的横杆，取得好的成绩。实验开始前，告知运动员实验目的和注意事项，运动员有5 min用于热身。整个实验过程中运动的质量和结果不反馈给运动员。为了更好地研究运动员撑杆跳的完成情况，在运动员的两髋、左脚踝、左膝盖附着标记点，如图3(b)所示。左脚踝和左膝盖处的标记点的位置信息用来描述运动员在团身即后仰举腿阶段，双腿的弯曲程度以及与身体的距离。由于在运动过程中可能会发生身体重心标记点被遮挡的现象，无法对重心直接进行跟踪，所以本文选择标记两髋，用其连线的中点近似人体重心。采集样本的过程中，如果没有完成过杆动作或是横杆被触碰落地，认为是过杆失败；否则记为成功过杆。每次的撑杆跳结果按序记录于文件中，且结果、质量不向运动员进行反馈。实验共采集200组数据样本，其中成功过杆153次，过杆失败47次。随机选取115组成功过杆的样本和35组过杆失败的样本，共150组构成一个训练集用于训练，剩余50组用于测试，并反复进行10次，共构成10组实验数据集。图4所示为一组实验数据集的数据构成。实验全程使用同一个撑杆、横杆。

图4 样本数据统计

2.3 ELM网络参数设置

2.3.1 输入向量和输出向量

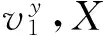
(16)

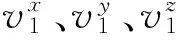
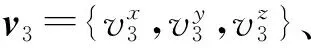
(17)

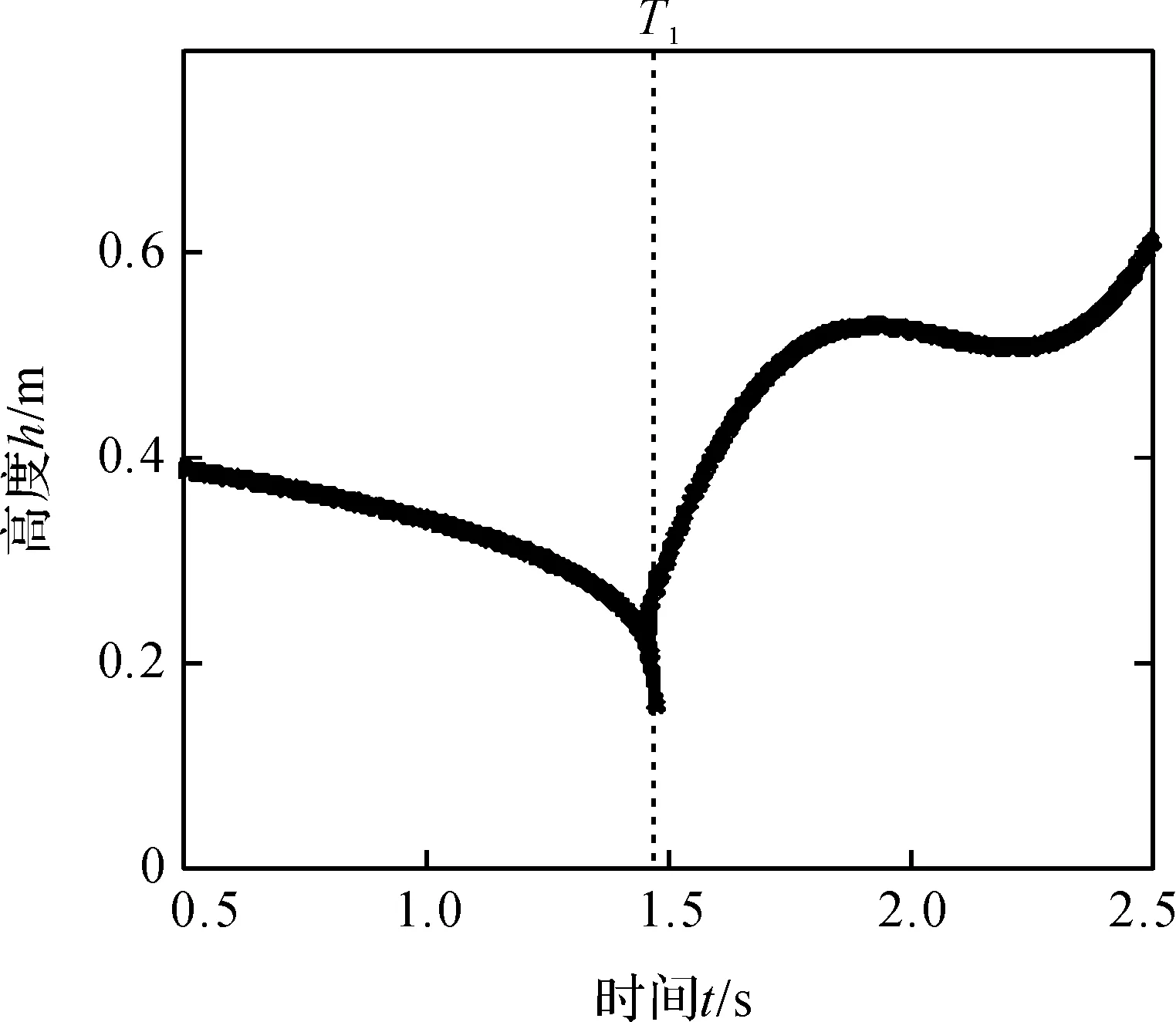
图5 助跑最后阶段到摆体前脚踝Y轴轨迹

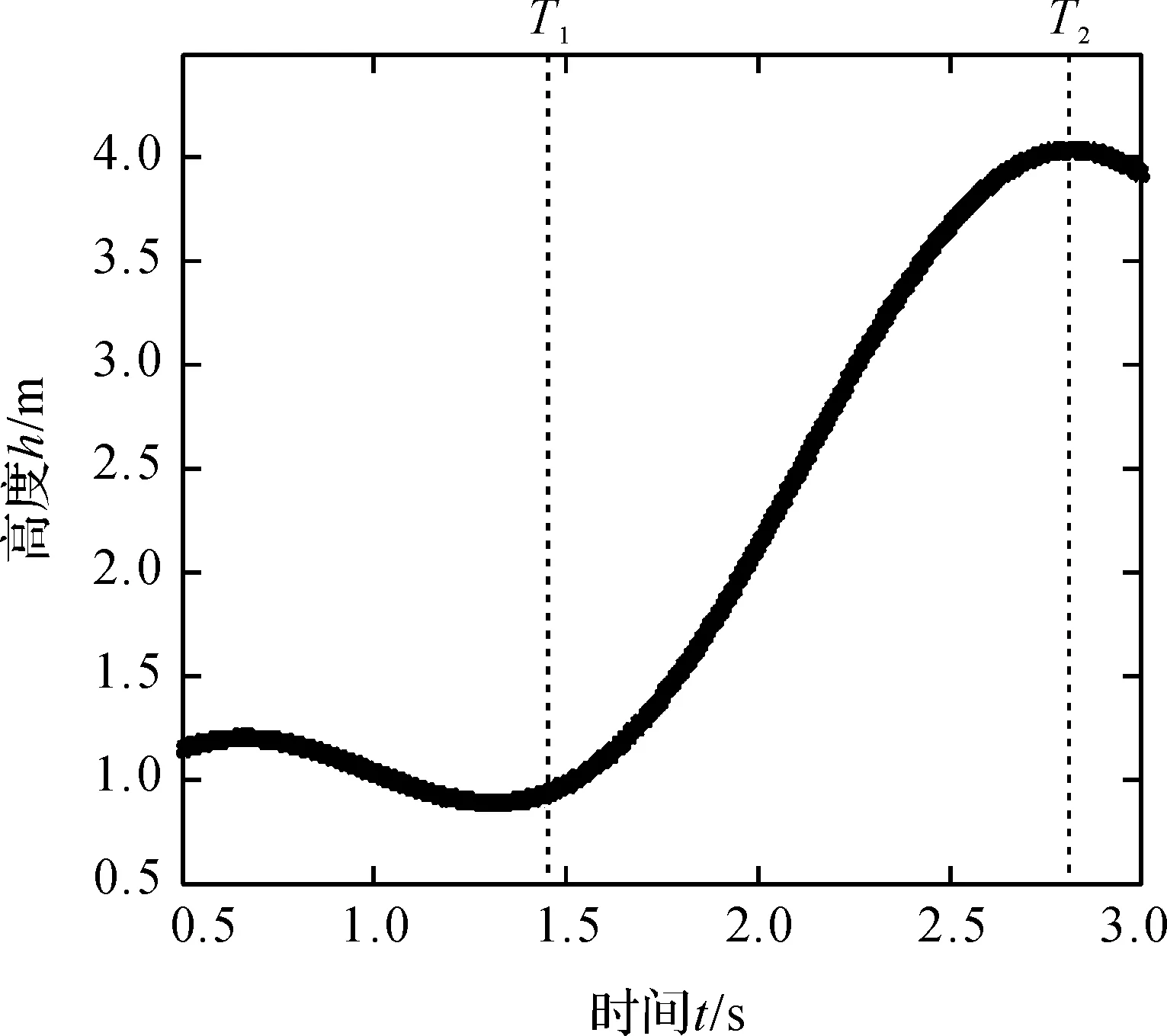
图6 身体重心Y轴轨迹

根据上述记录的信息，最终构成特征向量X={v1，θ1，v2，θ2，p20，v3，ly0，lx0}，所以模型的输入向量是一个16维的向量。对实验样本进行特征提取形成样本数据T={(Xi，Yi)}，i=1，2，…，200，其中输入向量Xi∈R16为第i组实验样本的提取的特征，输出向量为Yi∈{-1，1}，当Xi是成功过杆提取的特征时，Yi取1，否则取-1。

2.4 实验结果与分析

本文在Intel Xeon(R) E5-2620 v3 CPU 2.40 GHz，32.0 GB内存的机器上采用Matlab R2012a，实现了DE-RELM起跳过杆模型。本实验是在10组实验数据集下完成的以提高算法说服力。为方便讨论，本实验将DE算法中CR、F、NP以及迭代次数固定。经过大量实验最终本文选取CR=0.6，F=0.8。虽然搜索到全局最优解的概率会随着种群规模的增加而变大，但所需的计算量和计算时间也会随之增加，一般取100～300，本文取NP=200。在不影响算法性能的前提下，算法的最大迭代次数设为500。

隐层节点数对算法的影响见表1。从表2中可以看出，当迭代次数一定时，随着隐层节点数的增加，算法误差逐渐减低。当隐层节点数为10时，DE-RELM的误差率远小于ELM，当隐层节点数为15时，算法误差率虽有减小但变化不大，为减少算法计算量，选择隐层节点数为10的DE-RELM分类器与传统ELM和SVM支持向量机进行对比。为了提高算法的说服力，每个算法都执行10次，并记录平均值。

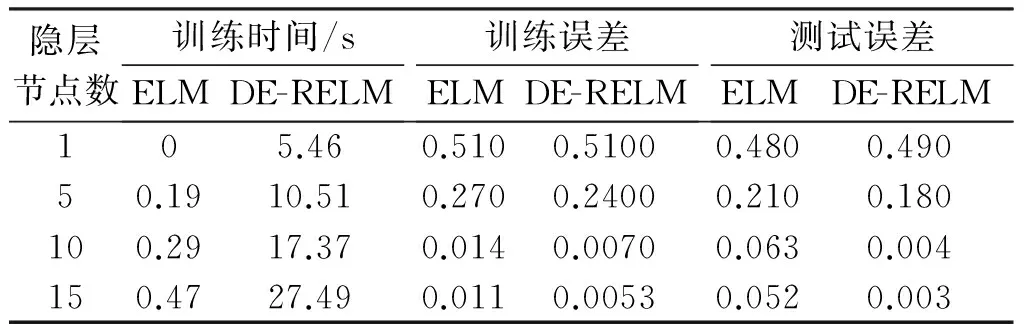
表1 隐层节点数对算法的影响

注：迭代次数为500次。

对10组实验数据集进行实验的结果见表2。可以看出，在迭代次数和隐层节点数一定时，DE-RELM算法的误差率更低，实验结果理想。

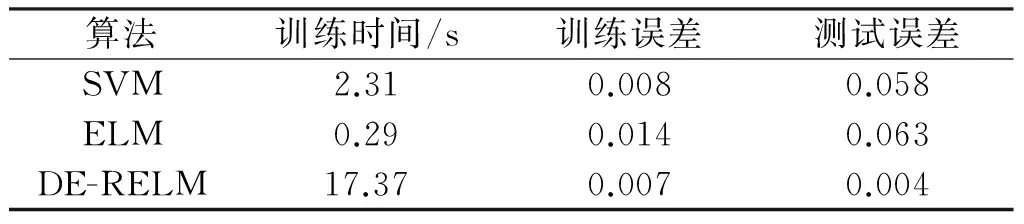
表2 三种算法性能对比

对50组测试样本分别使用ELM、SVM、DE-RELM三种算法进行分类，分类结果对比如图7所示。从各算法分类正确率可以看出每个分类器的分类效果。

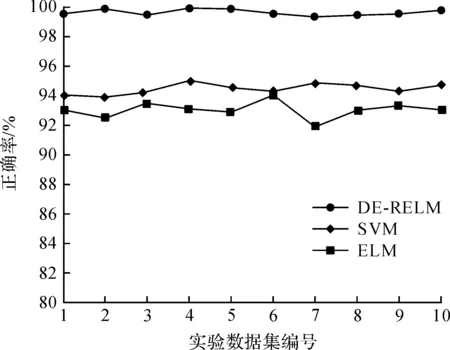
图7 各分类算法分类结果对比

10组实验数据集下不同测试样本数的平均分类准确率如图8所示。其中，横坐标为测试样本数，纵坐标为分类算法的正确率。

图8 各分类算法正确率分布

从图8可以看出三种分类算法对测试样本的分类情况。随着测试样本数量的增加，SVM和ELM的分类准确率都较高，泛化能力也都还好。但比较而言，DE-RELM的性能更佳，泛化能力更强，其分类准确率达到了99.61%，达到了实验预期的结果。

上述结果表明，本文提出的DE-RELM算法能够对撑杆跳高运动员是否成功过杆进行准确的分类、预测，且效果明显优于ELM、SVM算法。达到相同或更高的精度时，DE-RELM网络结构更优，泛化能力更好。

3 结 语

本文提出的DE-RELM模型能帮助提高撑杆跳高运动员起跳过杆技术。通过分析起跳过杆时提取的特征向量，并以此为参考依据进行训练。为提高模型的泛化能力，提升算法的性能，本文将差分进化算法和正则化的极限学习机进行了有机结合。实验表明，基于DE-RELM的起跳过杆模型性能远远优于ELM，具有很好的预测的能力，达到了预期目标，可以对运动员进行有效训练的指导。由仿真实验结果可知，本文提出的基于DE-RELM的撑杆跳起跳过杆模型有效。

[1] 陈庆杰，单吉谭.中国优秀女子撑竿跳高运动员技术研究现状[J].辽宁体育科技，2005，27(3):70-71.

[2] Fukushima T， Nishikawa S， Kuniyoshi Y. Active bending motion of pole vault robot to improve reachable height[C]//2014 IEEE International Conference on Robotics and Automation(ICRA). IEEE，2014:4208-4214.

[3] Liu G， Nguang S K， Zhang Y. Pole vault performance for anthropometric variability via a dynamical optimal control model[J]. Journal of Biomechanics，2011，44(3):436-441.

[4] Nishikawa S， Fukushima T， Kuniyoshi Y. Effective timing of swing-up motion by a pole-vaulting robot[C]//International Conference on Advanced Robotics. IEEE，2013:1-6.

[5] 李北玉.对影响撑竿跳高运动成绩的主要因素探讨[J].首都体育学院学报，2001，13(1):61-63.

[6] Huang G B， Zhu Q Y， Siew C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]//IEEE International Joint Conference on Neural Networks，2004. Proceedings. IEEE，2004，2:985-990.

[7] Huang G B， Zhu Q Y， Siew C K. Extreme learning machine: Theory and applications[J]. Neurocomputing，2006，70(1-3):489-501.

[8] 邓万宇，郑庆华，陈琳，等.神经网络极速学习方法研究[J].计算机学报，2010，33(2):279-287.

[9] 吴登国，李晓明.基于极限学习机的配电网重构[J].电力自动化设备，2013，33(2):47-51.

[10] Storn R， Price K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization，1997，11(4):341-359.

[11] 徐涛，郭威，吕宗磊，等.基于快速极限学习机和差分进化的机场噪声预测模型[J].电子与信息学报，2016，38(6):1512-1518.

[12] Chen S， Wu M， Zhao S. Analog circuit fault diagnosis based on DE OS-ELM[C]//Seventh International Symposium on Computational Intelligence and Design. IEEE，2014:509-513.

[13] 张智敏，孙南，张曼，等.撑杆跳高“自由起跳”技术评价的运动学参数分析[J].体育科技文献通报，2012，20(12):25-28.

[14] 陈庆杰，吕季东.我国优秀女子撑竿跳高运动员悬垂摆体技术的运动学特征[J].成都体育学院学报，2007，33(1):66-69.