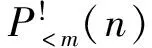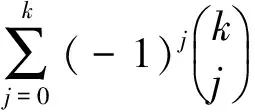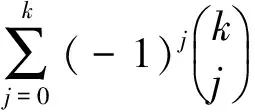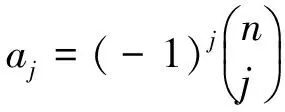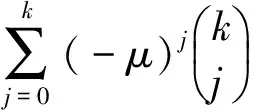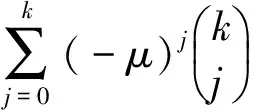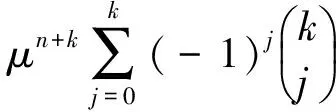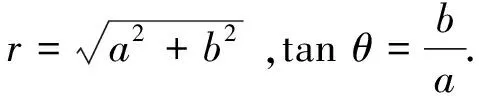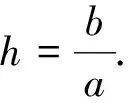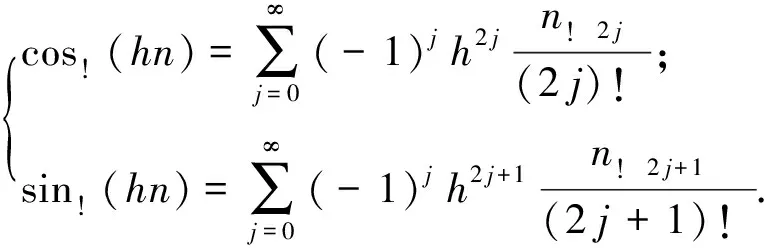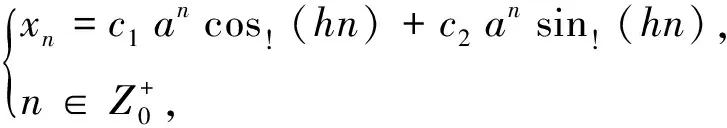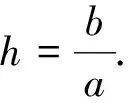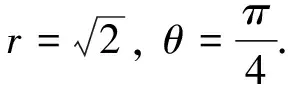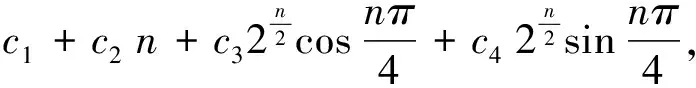解简单差分方程的方法及其改进

孙建新

(绍兴文理学院 数理信息学院，浙江 绍兴 312000)

文献[1]研究了拟初等函数，文献[2]研究了函数展开为阶乘幂级数的方法.下面可以看到，上述两种研究成果，可得到差分方程求解的新方法.因为新方法建议在差分方程中将所有的普通幂转换成阶乘幂，所以可以称新方法为“阶乘幂方法”.事实上，普通幂转换成阶乘幂，又相当于函数转换成拟初等函数，所以，新方法也可以称为“拟初等函数法”.

1 差分方程的两种形式

离散函数有两种表示方法.一种是函数法，即表示成自变量为非负整数的函数：

另一种是数列法，即下标法：

xn,yn,zn,n=0,1,2,….

差分方程也有两种表示形式，一种是仅使用向前(向后)差分算子 Δ()的方程形式，以线性差分方程为例，k阶差分方程可以表示为：

Δkxn+p1(n)Δk-1xn+…+

pk-1(n)Δxn+pk(n)xn=q(n);

pk-1(n)xn+pk(n)xn=q(n).

另一种是移位算子E的方程形式：

Ekxn+p1(n)Ek-1xn+…+

pk-1(n)Exn+pk(n)xn=q(n).

记I为恒等算子，则差分算子与移位算子满足如下关系：

Δ=E-I=E，

=I-E-1=E-1Δ；

E=I+Δ，

E-1=I-.

当系数pj(n)=aj(j=1,…,k)都与n无关时，就称其为常系数的；当q(n)=0时，就称其为齐次的.对于常系数的齐次线性差分方程的两种形式：

Δkxn+a1Δk-1xn+…+

ak-1Δxn+akxn=0;

(1)

Ekxn+b1Ek-1xn+…+

bk-1Exn+bkxn=0.

(2)

它们之间存在较简单的关系，即有如下定理：

定理1.1 设方程(1)的特征根为λj(j=1,…,k),方程(2)的特征根为μj(j=1,…,k)，则有

μj=λj+1,(j=1,2,…,k) .

证明方程(1)可以改写成

(Δk+a1Δk-1+…+ak-1Δ+akI)xn=0;

即

Δk+a1Δk-1+…+ak-1Δ+akI=0;

(Δ-λ1I)(Δ-λ2I)…(Δ-λkI)=0，

其中λj(j=1,…,k)为方程(1)的特征根，于是有

……

由Δ=E-I，方程(1)可化为

(E-I-λ1I)(E-I-λ2I)…

(E-I-λkI)=0;

(E-(1+λ1)I)(E-(1+λ2)I)…

(E-(1+λk)I)=0.

(3)

另一方面，由方程(2)可得

(Ek+b1Ek-1+…+bk-1E+bkI)xn=0;

Ek+b1Ek-1+…+bk-1E+bkI=0;

(E-μ1I)(E-μ2I)…(E-μkI)=0，

(4)

μj(j=1,…,k)

为方程(2)的特征根.于是有

……

比较式(3)和式(4)即得，证毕.

2 一阶差分方程

2.1 较简单的一阶差分方程

方程xn+1=axn+b，其中a，b为常数.

(ⅰ)当a=1时

xn+1=xn+b.

⑸

则有

可知满足方程的离散函数就是等差数列.

(ⅱ)当a≠1，b=0时

xn+1=axn,

(6)

则有

可知满足方程的离散函数就是等比数列.

(ⅲ)当a≠1，b≠0时

xn+1=axn+b,(a≠1，b≠0).

若记

(7)

x*称为差分方程的平衡点(或不动点).令

yn=xn-x*,

则有

yn+1=ayn.

(8)

比较式(6)与式(8)，可得

即

综合以上结果可得如下定理：

定理2.1 一阶差分方程

xn+1=axn+b, (a≠1).

2.2 一般的变系数一阶差分方程

仅考虑两个特例.

例1)xn+1=an2xn.

该差分方程的通解为

例2)xn+1=axn+bn+c.

定理2.2 一阶常系数非齐次线性差分方程

xn+1=axn+bn+c

的解为

其中

证明若a=1,则递推可得

xn=xn-1+b(n-1)+c=

xn-2+b(n-2)+b(n-1)+2c=…=

若a≠1,则

xn+1+A(n+1)+B=

axn+(bn+c)+An+A+B=

axn+(A+b)n+(A+B+c).

令

(A+b)n+(A+B+c)=a(An+B),

解得

此与定理2.2结果等价，命题获证.

例3)xn+1=3xn+2n+1,求差分方程的解.

解：由a=3,b=2,c=1, 即得A=1,B=1.于是

xn+1+(n+1)+1=3xn+2n+1+(n+2).

xn+1+(n+1)+1=3(xn+n+1).

令yn=xn+n+1.可得yn+1=3yn.则

yn=xn+n+1=3ny0=3n(x0+1),

解得

xn=yn-n-1=3n(x0+1)-n-1.

解：原方程可化为

(n+1)xn+1=2nxn.

令yn=nxn,则有

yn+1=2yn.

于是

yn=2ny0=2n(nx0).

解得

xn=2nx0.

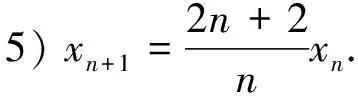
解：原方程可化为

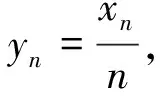
yn+1=2yn.

于是

yn=2n-1y1=2n-1x1.

解得

xn=n2n-1x1,n=1,2,….

3 常系数齐次线性差分方程的通解

对于常系数齐次线性差分方程来说，由定理1.1可知，存在差分形式(1)与移位算子形式(2).形式(2)又等价于：

xn+k+b1xn+k-1+…+bk-1xn+1+bkxn=0.

(9)

当q(n)≠0时，下面的方程

xn+k+b1xn+k-1+…+

bk-1xn+1+bkxn=q(n).

(10)

称为k阶常系数非齐次线性差分方程.式(9)称为与式(10)对应的齐次方程.

不妨设μ1，μ2，…，μk为方程(9)所对应的特征方程

μk+b1μk-1+…+bk-1μ+bk=0.

(11)

的特征根.下面是关于齐次方程(9)的通解的几个定理.

定理3.1 当特征根μ1，μ2，…，μk为k个互不相同的实根时，齐次方程(9)的通解为

(12)

证明考虑齐次线性差分方程的E形式(2),不妨设xn=μn, 则

Exn=Eμn=μn+1=μ·μn=μ·xn,

进而有

Ejxn=μj·xn,j=2,3,…,k.

于是方程(2)等价于

μkxn+b1μk-1xn+…+bk-1μxn+bkxn=0.

若xn=0，显然包括在通解(12)中(只要取c1=c2=…=ck=0)；若xn≠0，则必有特征方程(11)式成立.即齐次线性差分方程(2)的非零解,形如xn=μn(μ≠0).

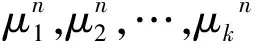
定理3.2 当特征根μ1，μ2，…，μk为k个相同的实根μ(即为k重实根)时，齐次方程(9)的通解为

xn=c1μn+c2nμn+…+

(13)

其中P

证明首先，由差分恒等式

可知

其中

cmn!0， (n!0=1).

其中S1(m,j)与S2(m,j)分别是第一类与第二类stirling数[5].于是

ΔkP

特别地，对于P

Δknm=(E-I)knm=

(m

(14)

其次，当μ是差分方程(2)的k重特征根时，有

当m

(E-μI)k(nmxn)=

(m

这就证明了nmxn(m=0,1,…,k-1)都是齐次方程(9)的解, 并且是线性无关的. 由于方程(9)是k阶常系数齐次线性差分方程，满足可加性，所以这些线性无关解的线性组合便是含k个参数的通解.(获证)

定理3.3 齐次方程

xn+2-2axn+1+(a2+b2)xn=0

的通解为

(15)

(16)

证明易知μ1=a+bi，μ2=a-bi 为方程的共轭复根，故齐次方程

xn+2-2axn+1+(a2+b2)xn=0

的通解可写成

令

则rncos(nθ)与rnsin(nθ)是两个线性无关的实离散函数，通解可以表示为两者的线性组合，即式(15)成立.

另一方面，齐次方程

xn+2-2axn+1+(a2+b2)xn=0

的通解也可写成

xn=c1(a+bi)n+c2(a-bi)n=

c1an(1+hi)n+c2an(1-hi)n,

由二项公式

利用定义(见式(16))

即得特征值为共轭复根时的通解的等价形式为

值得指出的是，尽管通解有两种形式，后面将发现：在确定非齐次差分方程的特解时，使用第二种形式(即拟初等函数形式)会给计算带来方便.

例6)求差分方程

xn+2-5xn+1+6xn=0

的通解.

解：对应特征方程为

μ2-5μ+6=0，

解得

μ1=2，

μ2=3≠μ1.

由定理3.1知通解为

例7)求差分方程

xn+2+6xn+1+9xn=0

的通解.

解：对应特征方程为

μ2+6μ+9=0，

解得

μ1=μ2=-3.

由定理3.2知通解为

xn=c1(-3)n+c2n(-3)n=

例8)求差分方程

xn+2-2xn+1+2xn=0

的通解.

解：对应特征方程为

μ2-2μ+2=0，

解得

μ1=1+i，

μ2=1-i.

a=b=1,

由定理3.3知通解为

即

例9)求差分方程

Δ4xn+Δ2xn=0

的通解.

解法1：差分算子对应的特征方程为

λ4+λ2=0.

即

λ2(λ2+1)=0.

解得

λ1=λ2=0，

λ3=i,

λ4=-i.

于是方程的通解为

xn=(c1+c2n)(1+0)n+

A3(1+i)n+A4(1-i)n=

解法2：差分方程Δ4xn+Δ2xn=0可以分两种情况：

或者 Δ2xn=0，此时更有 Δ4xn=0.可见 Δ2xn=0的解都是原方程的解.利用差分的逆运算“和分”[4]可得

xn=Δ-2(0)=P<2(n)=c1+c2n.

或者Δ2xn≠0，此时必有Δ2xn+xn=0. 可见Δ2xn=-xn的解也是原方程的解.考虑到拟初等函数满足[1]

Δ2cos!(n)=-cos!(n),

Δ2sin!(n)=- sin!(n),

可知cos!(n)与 sin!(n)是方程Δ2xn=-xn的两个线性无关解.于是方程Δ2xn=-xn的通解为

最后得到原方程的通解为

xn=c1+c2n+c3cos!(n)+c4sin!(n)=

其中

(17)

[1]孙建新.拟初等函数的差分性质及其应用[J].绍兴文理学院学报,2015,35(9):31-36.

[2]孙建新.函数展开为阶乘幂级数的方法[J].绍兴文理学院学报,2016,36(7):29-34.

[3]孙建新,胡金杰.阶乘幂的差分算子及其逆[J].绍兴文理学院学报,2005,25(7):22-25.

[4]孙建新.阶乘幂多项式及其基本恒等式[J].绍兴文理学院学报,2004,24(7):34-37.

[5]孙建新.stirling数的一个计算公式[J].绍兴师专学报,1986(2):46-51.