错位角对管内双螺旋扭带层流换热特性的影响
胡少永, 王宗勇, 谢文超, 王舒婷
(沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142)
由于煤、石油、天然气等不可再生资源储量有限,而能源的需求不断增长,能源短缺日益严重,节能降耗己经成为现代工业发展中的一个中心主题,同时也成为缓解当前能源危机的一个重要途径.换热器是工业生产中应用广泛的一种通用能源设备.采用各种强化传热手段的新型高效换热器可以大幅度降低设备投资和能耗,能够在同等功耗下获得更大的传热效率,是一种极其有效的节能降耗途径.管内插入扭带是一种简单实用且应用广泛的强化传热技术,由于它具有结构简单、性能稳定、装拆和维修方便等优点,国内外学者做了大量研究.传统扭带可以明显提高管内传热效果,但同时存在着很大的压降.为了克服传统扭带的缺点,增强换热效果并减小流动阻力,提高换热设备的综合换热性能,国内外众多研究者开发了多种新型结构扭带,如间断扭带[1-4]、中空扭带[5]、窄边扭带[6-8]、交替轴中空扭带[9]、打孔扭带[10]、多扭旋叶片[11-14]、偏心螺旋扭带[15]等.大量的研究结果表明这些新型扭带在提高对流传热系数同时,流动阻力也往往相应增加,综合换热性能提高非常有限,在某些条件下甚至会下降.
静态混合器由于混合效果好、维护费用低、能够实现连续生产工艺等优点,近年来在化工、制药、石油、造纸等领域得到了越来越广泛的应用.在众多静态混合器中Kenics混合器是工业化应用最广泛的一种类型,其混合元件(Kenics元件)是由一系列首尾相连并且在连接处相互垂直的螺旋短扭带构成.管内流体在Kenics元件的作用下在两个半圆形流道内螺旋流动,在进入下一元件时每个流道内的流体被一分为二,各取二分之一汇入同一流道螺旋流动,这样周而复始经过多个螺旋元件后,流体的均匀性得到显著提高,同时管内流体的对流传热性能也得到明显强化.
Kenics元件的混合和传热强化机理存在着较大的关联性,混合效果的好坏直接影响管内主流区流体均匀性和温度均匀性,进而影响管内流体的传热效果.Kenics型混合器实现混合主要存在三种方式,分别为反复分割和汇合的分布混合、径向对流混合及拉伸混合.在低雷诺数下,由于流体的流速较低或流体黏度较大,径向对流混合相对较弱,分布混合及拉伸混合特别是分布混合在流体的整个混合效果中起到决定性作用.多数研究者认为Kenics混合器的混合效果由混合元件个数决定,物料每流过混合元件一次,流束就被分割为原来的2倍,一直分割下去,最终达到要求的混合效果.实际上被混合物料的体积流量比对于一定混合长度所能取得的混合效果同样具有较大影响.对于混合元件结构一定的混合器而言,体积流量比越接近1越容易混合,混合效果越好,反之越差.大量的实验及工程应用结果表明,Kenics混合器在低雷诺数或物料流量比远离1的工况下,单位管长所能取得的混合效果较差,同时管内传热性能也下降.
管内物料的混合效果和传热性能对于磺化、硝化等强放热反应能否实现管式连续反应有着决定性的影响,因为这些强放热反应极其剧烈,反应过程释放出的大量反应热,必须及时快速地移出,才能保证反应的正常进行.同时,这类反应还有一个特点就是反应的停留时间比较长,通常在50 min以上,反应物料在管式反应器(混合器)内必须缓慢流动以尽可能降低反应管长度.物料低速流动往往会导致反应物料混合不充分,反应效果变差,同时传热系数降低,采用传统Kenics混合器作为强放热反应器很难满足管式连续反应工艺要求,为此本研究团队提出了一种新型的旋流式混合器——双螺旋扭带混合器.该混合器的混合元件是利用Kenics元件的混合机理改进得到,其结构是由一系列双螺旋扭带单元构成,相邻单元错开一定角度,每个单元内的两个扭带保持一定间距并且处处平行.物料进入到该混合器后,在双螺旋扭带作用下一分为三,每经过一个混合单元分割的层数扩大3倍.与其它类型扰流元件相比,主流区域流体混合更加均匀,传热效果更好.初步研究结果表明:在低雷诺数下,双螺旋扭带混合器及Kenics混合器在均采用6个混合单元、相邻单元错位角为90°的情况下,前者的混合效果相对于后者提高约30 %,传热系数提高10 %左右.
尽管初步研究表明双螺旋扭带具有良好的混合及传热效果,但其结构对传热性能的影响仍有待进一步研究.为了进一步确定错位角对双螺旋扭带传热性能及流动特性的影响,更好地指导双螺旋扭带反应器的结构设计,拓展其在强放热反应领域的工业化应用,本文采用数值模拟方法,对不同交错角下的双螺旋扭带的层流换热特性进行研究,旨在更深入地了解双螺旋扭带传热强化机理.
1 数值模拟方法
1.1 模拟对象与方法
双螺旋扭带是由一系列首尾相连、旋向相同的双螺旋单元构成.每个双螺旋单元具有两片相互平行且保持一定间距的短螺旋扭带,在一个单元长度范围双螺旋扭带相对扭转180°,将管内空间分割成三个独立的螺旋通道.相邻单元错开一定角度,该角度称为错位角(θ),几何模型如图1所示.

图1 双螺旋扭带的几何模型
双扭带厚度均为1 mm,圆管内径D=20 mm,长度L=80 mm,扭带与圆管内壁贴合没有间隙,宽度取决于两平行板间距.双扭带的长径比(定义为双螺旋单元的长度H与圆管内径D之比)为2.0,间隙比(定义为双扭带间距C与圆管D之比)为0.15,相邻单元的错位角θ分别取0°、30°、45°、60°和90°.
采用Fluent6.3.26进行数值模拟.管壁为恒热流边界(热流密度为6 000 W/m2),管子进出口采用周期性边界条件.工作介质为水,给定质量流量,保证Re的范围为100~1200,采用管内径为雷诺数的特征尺寸,初始温度为300 K.压力和速度的藕合采用SIMPLE算法,残差控制在10-6以下.
1.2 数据处理方法
在对强化传热技术进行性能评价时,综合考虑换热能力(Nu)和流动阻力系数(f),采用传热强化比PEC对强化管和光管在相同功耗下的换热效果进行比较.当PEC>1时,表明在同样的输送功耗下,强化管比光管具有更好的热-水力学综合性能;反之,光管的热-水力学综合性能更好.换热能力(Nu)、流动阻力系数(f)和传热强化比PEC分别定义如下:

(1)
式中:h—流体的对流传热系数,W/(m2·K);D—管子的内径,m;λ—流体的导热系数,W/(m·K);q—热流密度,W/m2;Tw—管壁面温度,K;Tf—管内流体温度,K.

(2)
式中:Δp—压力降,Pa;ρ—流体的密度,kg/m3;v—流体平均速度,m/s;L—管子的长度,m.

(3)
式中:Nu—内置扭带圆管的Nusselt数;f—内置扭带圆管的阻力系数;Nu0—光管对应的Nusselt数;f0—光管的阻力系数.
由于采用恒热流边界条件,且流动状态为层流,因此,Nu0和f0分别为:
Nu0=4.36
(4)

(5)
1.3 模拟方法验证
为保证模拟方法的可靠性,用相同条件下的光管进行了数值模拟,将不同Re数下的努塞尔数和阻力系数的模拟值与理论值进行了对比分析,结果表明两者的误差均在1 %以内(如图2所示),验证了模拟方法是正确可靠的.

图2 光管模拟值与理论值比较
1.4 网格无关化验证
计算模型采用四面体网格,在雷诺数及螺旋元件结构参数一定的条件下,通过改变网格尺寸考察其对努塞尔数和阻力系数的影响来确定网格无关性.在Re=400,中间间隙比为0.15和长径比为2.0时,网格大小分别设置为1.3、1.0、0.75、0.65,分别对应69 692、136 488、286 988和512 106个网格数.由图3可以看出:当网格数从286 988变至512 106时,随着网格数的增加,努塞尔数Nu和阻力系数f变化很小,表明网格大小对计算结果可以忽略不计,因此,计算网格大小采用0.75是合适的.

图3 网格数与Nu和f的关系
2 结果与分析
2.1 错位角对传热及流动阻力的影响
相邻螺旋单元之间的错位角主要影响前一单元内流体进入下一单元的流体分配和速度分布,进而形成不同的传热特性和流动阻力.为了确定错位角对传热特性和流动阻力的影响规律,在Re=100~1 200范围内对不同错位角下的Nusselt数、阻力系数及传热强化比PEC进行了计算.
由图4可以看出:当Reynolds数较低时(Re≤400),错位角为0°的双螺旋扭带即连续螺旋扭带的Nu数高于其它错位角扭带,其它错位角扭带之间Nu数差别不大.在Re=200时,连续扭带的Nu数比其它错位扭带高11.0 %~22.5 %.随着雷诺数的增大,当Re=500~1 200时,连续扭带与错位扭带之间的关系发生了逆转,所有的错位扭带的Nu数均高于未错位的连续扭带,并且从图中还可看到在该雷诺数范围内最高Nu数的错位角为60°,与连续扭带相比Nu数提高2 %~12 %,雷诺数越大提高幅度越明显,这与工程上应用最为广泛的Kenics型螺旋元件的90°错位角存在明显的差别,值得引起研发设计人员的注意并进行更为深入的研究.
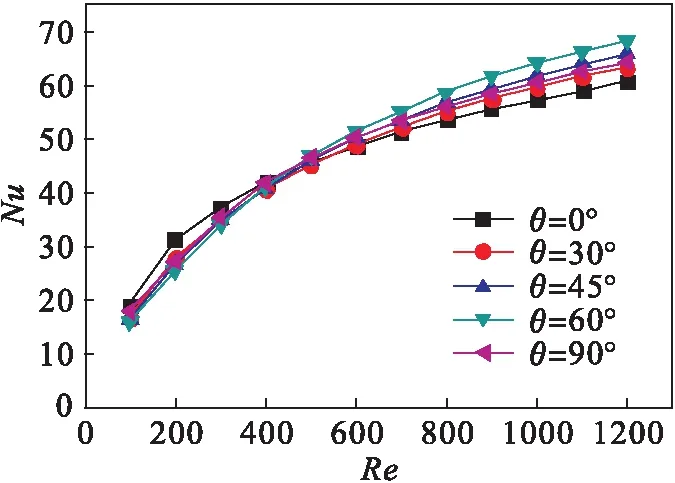
图4 内置双螺旋扭带的圆管内Nu随Re的变化规律
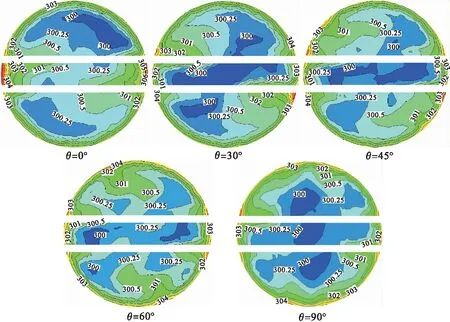
形成图4所示的传热强化状况还应从螺旋扭带的传热强化机理角度进行分析:错位角为0°的连续扭带,其传热强化主要是扭带迫使流体整体螺旋流动的同时增强了流体的径向流动,即形成了螺旋涡流,使传热边界层内的流体得到扰动和更新,这种强化作用随着雷诺数的增大而增强;由图4可以看出Nu数是随着雷诺数增大逐渐增大的;而具有一定错位角的交错扭带除了具有上述旋流传热强化作用之外还有对流体的切割作用,切割作用对传热强化具有两面性,首先,切割会使上一螺旋单元形成的螺旋涡流破裂为两个螺旋涡流,由于扭带的阻碍在一定的长度范围涡流强度会有所削弱,对传热实际起到了弱化作用,这种弱化作用在低雷诺数下表现得更为明显;其次,扭带将上一流道内的流体切割开来的同时使其进入到了下一螺旋单元的不同流道,实现了流体的分布混合,提高了核心区和边界层内流体的温度均匀度,对传热实际起到了强化作用,这种强化作用在较高雷诺数下作用显著.扭带的这种弱化和强化作用在图中均已表现出来,在较低的Reynolds数(Re≤400)下,交错扭带弱化了旋流强度,所有非0°错位角扭带的Nu数均低于传统连续扭带;而较高雷诺数(Re>500)下扭带的分布强化作用起到主导作用,致使交错扭带的Nu数均高于连续扭带;在400 不同错位角的各扭带传热强化差异主要是由各流道的速度分布决定的,即取决于各流道内螺旋涡流的位置和强度.而流道的速度分布除了与错位角相关之外,还与双螺旋扭带的间隙比和长径比存在着必然联系,在本文的结构参数下,60°错位角在较高雷诺数下传热效果最佳,但这并不代表在其他结构参数下也得到相同结论. 螺旋扭带在强化传热的同时也会使流动阻力增加,特别是双螺旋扭带相比于传统螺旋扭带增大了流体接触面积,摩擦阻力势必会增大,因此,很有必要对其流动阻力特性进行分析.由图5可见:各种错位角下螺旋扭带的阻力系数随Re变化的规律是相同的,任何交错扭带的阻力系数均高于连续扭带,并且随着错位角的增大阻力系数也相应增大.交错扭带的流动阻力大于连续扭带的原因比较简单,相邻螺旋单元错开一定角度后,除了原有的流体摩擦阻力之外,后面单元的螺旋片对流体的分割阻挡形成了形体阻力,两者叠加的结果必然导致交错扭带的阻力大于连续扭带.错位角增大流动阻力相应增大是由于双螺旋扭带所形成的三个流道是轴对称的,对称轴通过管中心并与螺旋片垂直,各流道由于这种对称关系在雷诺数不是很高的情况下,流动中心(最大轴向速度位置)必然位于对称轴上,当错位为90°时,下游螺旋片恰好位于上游螺旋流道的速度中心,在这种情况下螺旋片的形体最大,当错位角减小,下游的螺旋片逐渐偏离速度中心,相应的形体阻力也会逐渐减小,因此,形成了错位角增大流动阻力相应增大的这种变化规律. 图5 内置双螺旋扭带的圆管内f随Re的变化规律 交错扭带在一定的雷诺数范围内能够提高对流传热性能,但同时也增大流动阻力,从能效角度很有必要对其进行综合考虑.PEC传热性能评价准则(公式3)也可称为传热强化比,利用该指标来分析双螺旋扭带的综合传热强化性能,其结果如图6所示.由图6可知:双螺旋扭带的PEC最小值为1.62,最大可达5.0以上,均高于1.0;当Re≤900时,错位角为0°的双螺旋扭带(连续扭带)综合性能最好;Re=900~1 200时,60°错位角对应的PEC值最高,说明在较高雷诺数的层流状态下60°错位角的双螺旋扭带可以获得最佳的综合传热性能.由图6还可看出:Re>500情况下,90°错位角的双螺旋扭带的综合传热性能最差,而在将交错扭带用于混合强化时,90°错位角往往是最佳的,在工程应用当中应根据使用目的的不同采用不同的错位角. 图6 内置双螺旋扭带的圆管内PEC随Re的变化规律 双螺旋扭带的传热特性实际取决于管内流体的流动特性,即与管内流体的速度分布密不可分.为了深入解释错位角对螺旋扭带的强化换热效果的影响,在Re=1 000的情况下,选取L=80 mm横截面的速度场和温度场为研究对象,利用其分布规律分析形成上述传热特性的机理. 由图7可见:连续扭带两侧的弓形流道的速度中心靠近流动方向右侧的角点附近,流动速度较大,而中间的近似矩形流道的速度中心位于形心位置,这种现象说明两侧流道流体的旋流强度较大,而中间流道相对较小,这与中间流道宽度较窄边壁摩擦阻力大有关;随着错位角的增大,两侧流道速度中心逐渐向逆时针方向偏移,高速区域范围扩大,错位角达到60°时,两侧流道出现三个高速流动区域,随着错位角的进一步增大,两侧流道的高速区域发生合并,右侧角点附近的高速区域消失,左侧角度附近的高速区域的速度增大.对于中间流道而言,错位角增大提高了流道的流动速度.当错位角达到60°时,中间流道流速达到最大,靠近圆管壁面两侧形成两个高速区域.形成这种流动现象的原因是下游双螺旋扭带错开一定角度后,将两侧流道的高速流体分割开来,迫使其进入流速较低的中间流道或下游两侧流道的低速位置,这样使圆管内整个横截面内的流速得到均布.当错位角达到60°时,速度分布最为均匀,这就从流体速度分布角度说明了60°错位角传热Nu数最高的原因. 图7 Re=1 000时内置双螺旋扭带的圆管横截面轴向速度场 Re=1 000时内置双螺旋扭带的圆管横截面温度场如图8所示. 图8 Re=1 000时内置双螺旋扭带的圆管横截面温度场 由图8可知:连续扭带的中间流道靠近圆管壁厚处的温度梯度较小,低温流体集中在流道中心附近;但随着错位角的增大,中间流道低温区域扩大,靠近圆管壁面的温度梯度显著增大.对于两侧流道而言,错位角增大对其内部的温度分布的影响规律性不是十分明显,但仔细观察也可看到错位角为60°和45°时两侧流道的温度均匀性较好,而其它的错位角的温度均匀性较差.这从温度分布角度说明了在该雷诺数下,60°错位角的螺旋扭带的传热效果最好. 图7和图8的分析结果表明:增大核心流体的温度和速度均匀性能够提高螺旋扭带的传热强化能力,双螺旋扭带的结构设计必须保证这一点才能具有工程应用价值. 在基于管内双螺旋扭带间隙比和长径比不变的基础上,对不同错位角的双螺旋扭带在Re=100~1 200的层流换热特性进行了数值模拟和比较分析. (1) 当Reynolds数较低时(Re≤400),错位的双螺旋扭带的换热效果(Nu)要比未错位的连续扭带差;但在较高Reynolds数时(Re=500~1 200),错位的双螺旋扭带的换热效果要比未错位的情况好很多,相比未错位扭带的换热性能可以提高2 %~12 %. (2) 阻力系数f随扭带错位角的增大而增大,但是随着错位角度的增大,阻力的增加的幅度越来越小. (3) 传热强化比PEC随扭带错位角的变化趋势与Nu不大相同,当Re≤900时,未错位扭带综合性能最好;Re=1 000~1 200时,60°错位角对应的扭带综合性能最好;Re>500情况下,90°错位角的双螺旋扭带的综合传热性能最差. (4) 在较低Re下采用未错位双螺旋扭带能获得优良的传热及流动综合性能;而较高Re下,错位角为60°所对应的扭带的综合性能最好. [1] SAHA S K,GAITONDE U N,DATE A W.Heat Transfer and Pressure Drop Characteristics of Laminar Flow in a Circular Tube Fitted with Regularly Spaced Twisted-tape Elements[J].Experimental Thermal and Fluid Science,1989,2(3):310-322. [2] EIAMSA-ARD S,THIANPONG C,PROMVONGE P.Experimental Investigation of Heat Transfer and Flow Friction in a Circular Tube Fitted with Regularly Spaced Twisted Tape Elements[J].International Communications in Heat Mass Transfer,2006,33(10):1225-1233. [3] SAHA S K,DUTTA A,DHAL S K.Friction and Heat Transfer Characteristics of Laminar Swirl Flow through a Circular Tube Fitted with Regularly Spaced Twisted-tape Elements[J].International Journal of Heat and Mass Transfer,2001,44(22):4211-4223. [4] JAISANKAR S,RADHAKRISHNAN T K,SHEEBA K N.Experimental Studies on Heat Transfer and Friction Factor Characteristics of Thermosyphon Solar Water Heater System Fitted with Spacer at the Trailing Edge of Twisted Tapes[J].Applied Thermal Engineering,2009,29(5/6):1224-1231. [5] GUO J,FAN A W,ZHANG X Y,et al.A Numerical Study on Heat Transfer and Friction Factor Characteristics of Laminar Flow in a Circular Tube Fitted with Center-cleared Twisted Tape[J].International Journal of Thermal Sciences,2011,50(7):1263-1270. [6] AYUB Z H,Al-FAHED S F.The Effect of Gap Width between Horizontal Tube and Twisted Tape on the Pressure Drop in Turbulent Water Flow[J].International Journal of Heat and Fluid Flow,1993,14(1):64-67. [7] EIAMSA-ARD S,WONGCHAREE K,SRIPATTANAPIPAT S.3-D Numerical Simulation of Swirling Flow and Convective Heat Transfer in a Circular Tube Induced by Means of Loose-fit Twisted Tapes[J].International Communications in Heat and Mass Transfer,2009,36(9):947-955. [8] LIU W,YANG K,LIU Z C,et al.Mechanism of Heat Transfer Enhancement in the Core Flow of a Tube and Its Numerical Simulation[J].The Open Transport Phenomena Journal,2010,2(1):9-15. [9] 王特,王飞龙,范爱武,等.内置交替轴扭带的管内层流换热特性[J].化工学报,2014,65(S1):316-322. [10] RAHIMI M,SHABANIAN S R,ALSAIRAFI A A.Experimental and CFD Studies on Heat Transfer and Friction Factor Characteristics of a Tube Equipped with Modified Twisted Tape Inserts[J].Chemical Engineering and Processing,2009,48(3):762-770. [11] 张静,康铁鑫,龚斌,等.双扭旋叶片组合形式对管内湍流换热性能的影响[J].化工学报,2011,62(S2):52-60. [12] 龚斌,张静,张春梅,等.扭旋叶片组合对静态混合器流场特性影响[J].北京化工大学学报(自然科学版),2008,35(3):84-88. [13] 张静,吴剑华,龚斌.扭旋叶片组合方式对静态混合器湍流传热性能的模拟分析[J].机械工程师,2012(2):50-52. [14] 吴剑华,张静,张春梅,等.四叶片组合静态混合器湍流传热性能的数值模拟分析[J].过程工程学报,2009,9(1):7-11. [15] 王宗勇,朱军,田瑞,等.内置偏心螺旋扭带的管内层流流动特性[J].北京化工大学学报(自然科学版),2015,42(1):50-56.

2.2 速度场和温度场分析

3 结 论

