一种求解旅行商问题的改进粒子群算法
罗金炎
(闽江学院 数学系, 福建 福州 350108)
旅行商问题(TSP)是组合优化领域中经典的NP难问题[1],具有很强的现实意义.由于在许多领域都有广泛的应用,如计算机网络设计、通信节点设置、集成电路布线、物流配送等,因而一直以来是研究热点,为解决实际问题,广大研究者提出了许多求解算法(精确式或启发式).精确式算法能够得到问题最优解,但是需要与问题维数成指数级增长的时间成本,所能够求解的问题规模非常有限.启发式算法也称作近似算法,它以牺牲找到最优解的保证为代价,在合理的时间内找到近似解甚至最优解,其求解复杂度多是多项式阶数的.随着人工智能的发展,许多智能优化算法应用于TSP问题的求解,取得了较好结果.比如神经网络算法[2]、模拟退火算法[3]、禁忌搜索算法[4]、遗传算法[5]、蚁群算法[6]、粒子群算法[7]等.这些智能优化算法求解TSP问题,大多采用二进制编码求解0-1整数规划问题的思路进行寻优.本文利用等式约束规划问题K-T点的一个充分条件,将TSP问题的线性等式约束非线性规划进行降维使之转化为无约束极大极小优化问题.并基于基因调节原理运用外推技巧来改进粒子群算法,新的算法通过利用不同位置粒子的差异来引导外推方向,采用满足有限平方和准则的动态调节因子并在速度项中添加高斯扰动,来提高算法的寻优效率.数值实验结果验证了本文提出算法的有效性并具有较好的收敛效率.
1 等式约束规划问题K-T点的一个充分条件
规划问题
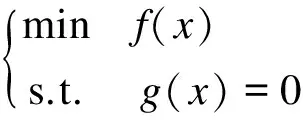
(1)



定理1[9]: 若x*∈Rn是方程组
的解,且M(x*)非奇异,则x*是上述规划问题(1)的K-T点.即
其中λ=-[M(x*)]TQ(x*).
2 TSP问题模型分析
TSP问题一般性描述为:给定n个城市以及任意两个城市之间的距离,寻求一条经过所有城市的最短访问路径,每个城市必须访问且只能访问一次.其图论描述为:给定图G=(V,A),其中V为顶点集,A为各顶点相互连接组成的弧集,已知各个顶点连接距离,要求一条长度最短的Hamilton回路.设dij为城市i与j之间的距离,即弧(i,j)的长度 (i≠j),当i=j时cij为足够大的数.引入决策变量
那么TSP问题的数学模型可表示为[7]:

(2)
其中上述模型可进一步松弛为如下连续问题[8]:
(3)
因是线性规划模型,线性规划的可行解集是一个凸集,最优解通常在边界上取得,即在x=0或x=1上取得,所以式(3)等价于式(2).为便于分析,上述模型可以进一步整理为如下线性等式约束的非线性规划问题的矩阵形式:
(4)
其中:CT=(c11,c12,…,c1n,c21,c22,…,c2n,…,cn1,cn1,…,cnn),x=(x11,x12,…,x1n,x21,x22,…,x2n,…,xn1,xn1,…,xnn).
令m=2n,k=n2,则
f:Rk→R,
p=k-m.
这里g(x)=Ax-b,则有g(x)=(Ax-b)=A.文献[9]中指出约束函数g(x)在点x*的frechet导数g(x*)需要有一个m阶子块是非奇异的(即秩A=m),记
根据定理1,可将上述求解等式约束规划问题(4)转化为求解非线性方程组:
或
(5)
应用无约束优化方法求解非线性方程组(5)时,通常可以将其转换为求解:
(6)
当p=2时,此为非线性最小二乘问题;当p=∞ 时,此为无约束极大极小优化问题:
(7)
极大极小问题(7)为非光滑优化问题,应用PSO算法可以有效求解此类问题[10],可以不必构造可微光滑函数,以式(7)为粒子的适应度函数,函数值越小表示适应度越高.
3 改进的粒子群算法设计
3.1 粒子群算法[11]
粒子群算法与其他进化类算法相似, 采用“群体”与“进化”的概念, 同时依据个体的适应值大小进行操作. 不同的是, 粒子群算法不像其他进化算法那样对于个体使用进化算子, 而是将每个个体看作是在搜索空间中的一个没有质量和体积的粒子, 并在搜索空间中以一定的速度飞行.每个粒子的飞行速度由其本身的飞行经验和群体的飞行经验调整.经典粒子群算法根据公式(8)进行迭代更新,粒子在解空间内不断跟踪个体极值和邻域极值进行搜索, 直到满足迭代停止条件, 即达到规定的迭代次数或满足规定的误差标准.

(8)
(9)
其中:w为惯性权重; rand()为均匀分布在(0,1)之间的随机数;c1和c2为学习因子.粒子的速度vi被最大速度Vmax所限制,即若vi>Vmax,则令vi=Vmax,而若vi<-Vmax,也令vi=Vmax.
3.2 粒子群算法位置更新公式的改进
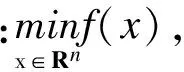
x3i=x1i+α(x1i-x2i)
(10)
其中α为调节因子,它决定调节的幅度,一般不能过大取大于零的小正数,来确保f(x3) 利用不同位置粒子的差异来引导外推方向.在由粒子群算法产生新位置时,再依据算法位置更新公式(9)产生另一个虚拟位置(在粒子尚未达到最优点时,对连续函数来说在附件存在更优的点): (11) 其中rand()为[0,1]内服从均匀分布的随机数. 根据外推技巧由式(10)和式(11)有: (12) 一般地,在起初阶段距离最优解较远,调节幅度较大有利于加速进化,而在后期距离最优解较近时,调节幅度应较小些.对多变量优化问题,由于每个粒子的位置分量较多,容易出现某些分量非常接近甚至相同的两个粒子,对此外推技巧将不起作用,在具体操作中需要在式(12)加上一个微小扰动.基于此(上述两点),调节因子采用动态递减满足随机递推算法[13]的数列因子,并在算法中的速度项部分添加高斯扰动.最后得到的位置公式为: (13) 步骤1:确定矩阵M和N,进一步确定矩阵P和Q,利用式(7)作为适应值函数; 步骤2:初始化种群N的粒子群,包括每个粒子的位置和速度,计算适应值函数,并记录粒子的个体历史最优位置和种群全局最优位置; 步骤3:根据式(8)和式(13)分别更新粒子的速度和位置,计算位置更新后的适应值函数,并与其个体历史最优值相比较,若更优,则更新粒子的个体历史最优位置,否则不变; 步骤4:将粒子的个体历史最优与种群的全局最优进行比较,若更优,则更新种群全局最优位置,否则不变; 步骤5:如果满足算法的终止条件|xk-xk-1|<ε,则输出全局最优解,否则转到步骤3继续执行. 为确保产生整数解,继续下面的步骤: (14) 步骤9:如果m (15) 步骤10:计算最优路径结果值,记录迄今为止的最优解.检查是否达到最大迭代步数,若是则结束,否则转步骤3. 为了验证算法的效果性能,先采用10节点的小样本TSP问题对算法的有效性进行验证,其节点位置如图1所示. 图1 10城市节点位置 算法进行了50次实验,最大迭代次数100,均能得到最优解,最快迭代次数为16次,得到的连续最优解矩阵为: 图2 算法搜寻到的最优路径 为进一步比较算法的性能,从TSPLIB标准库(http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95)中选取部分经典实例,使用Matlab 6.5编程,在CPU为AMD1.65 GHz内存为2 GB的计算机上进行仿真实验.最大迭代次数为1 000,实验测试100次.分别与PSO[14]、改进的FOA[15]进行比较,实验结果如表1和表2所示,OPT是已知最优值. 表1 本文算法求解TSP算例的仿真结果 表2 算法求解不同TSP算例的比较结果 从表2最优值和平均值的对比可以看出:本文算法对于不同规模的TSP问题均能寻优搜索到最优路径,充分反映了本文算法寻优的有效性.本文算法的偏差均比其他2个算法小,表明本文算法具有良好的全局收敛能力,这是因为算法速度项部分添加高斯扰动能够较好地避免算法陷入局部最优而早熟;从平均迭代次数指标上表明本文算法寻优速度具明显优势,这是因为算法的动态调节因子序列满足有限平方和准则,其选取策略对于迭代序列的收敛行为起着关键作用.通过程序的仿真实验,本文算法解决部分实例的最优路径如图3~图5所示. 图3 Bays29的最优路径 图4 Berlin52的最优路径 图5 Gr96的最优路径 利用等式约束问题K-T点的一个充分条件,将TSP问题的线性等式约束非线性规划进行降维使之转化为无约束极大极小优化问题,并基于基因调节原理运用外推技巧来改进粒子群算法,新的算法通过加强对进化方向的引导,采用满足有限平方和准则的动态递减调节因子,并在速度项中添加高斯扰动,提高了算法的寻优效率,数值实验结果验证了本文提出算法的有效性并具有较好的收敛效果. [1] GRECO F.Travelling Salesman Problem[M].Croatia:In-Teh,2008:36-39. [2] LI M L,YI Z,ZHU M.Solving TSP by Using Lotka-Volterra Neural Networks[J].Neurocomputing,2009,72(16):3873-3880. [3] 张盛意,蔡之华,占志刚,等.基于改进模拟退火的遗传算法求解0-1背包问题[J].微电子与计算机,2011,28(2):61-64. [4] GLOVER F.Future Paths for Integer Programming and Links to Artifical Intelligence[J].Computers and Operations Research,1986,13(5) :533-549. [5] 于莹莹,陈燕,李桃迎,等.改进的遗传算法求解旅行商问题[J].控制与决策,2014,29(8):1483-1488. [7] HOPFIELD J J,TANK D W.“Neural” Computation of Decisions in Optimization Problems[J].Biological Cybernetics,1985,52(3):141-152. [8] DANG C Y,XU L.A Lagrange Multiplier and Hopfield-Type Barrier Function Method for the Traveling Salesman Problem[J].Neural Computation,2001,14(2):303-324. [9] 李泽民.最优化问题的一种新途径[J].重庆建筑工程学院学报,1990,12(1):49-55. [10] 张建科,李立峰,周畅,等.一类非线性极小极大问题的改进粒子群算法[J].计算机应用,2008,28(5):1194-1196. [11] 曾建潮,介倩,崔志华,等.微粒群算法[M].北京:科学出版社,2004:7-8. [12] 王湘中,喻寿益,贺素良,等.一种强引导进化型遗传算法[J].控制与决策,2004,19(7):705-798. [13] 聂赞坎,徐宗本.随机逼近及自适应算法[M].北京:科学出版社,2003:23-28. [14] MARINAKI S Y,MARINAKI M.A Hybrid Multi-Swarm Particle Swarm Optimization Algorithm for the Probabilistic Traveling Salesman Problem[J].Comput Oper Res,2010,37(3):432-442. [15] 段艳明,肖辉辉.求解TSP问题的改进果蝇优化算法[J].计算机工程与应用,2016,52(6):144-149.

3.3 求解TSP的改进粒子群算法具体步骤



4 仿真实验
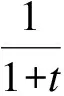
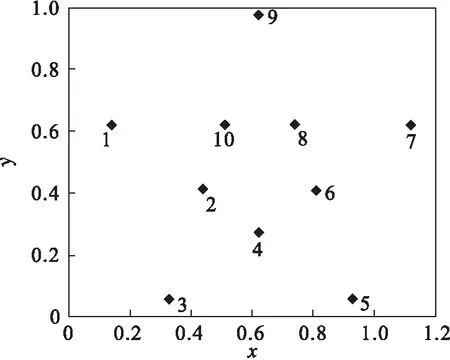
4.1 算法有效性测试,10个城市的旅行商问题

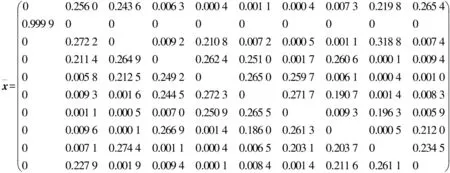



4.2 算法性能比较


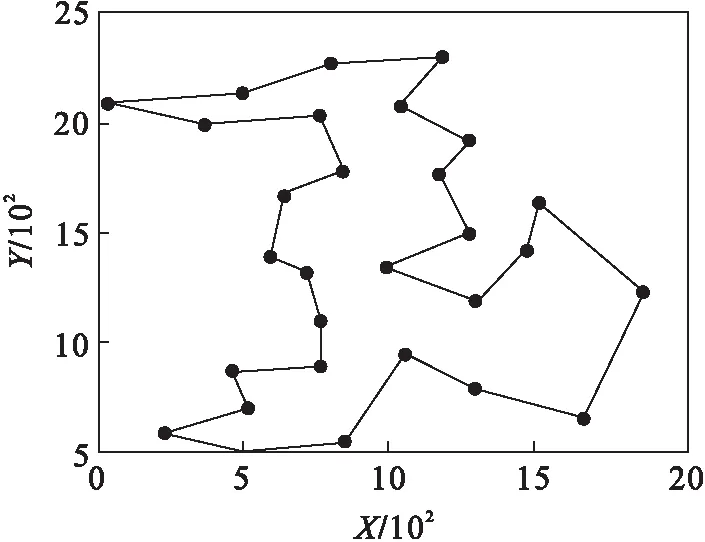


5 结 论

