核正交局部保持投影算法及应用仿真研究

郭金玉， 韩建斌， 李 元

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

随着生产力的发展，化工过程变得日趋集成化和复杂化.及时而有效地检测出故障对于保证产品质量、生产安全都有着至关重要的作用.近年来，多变量统计学作为一种有效的数据驱动方法，已成功应用于化工过程检测与监视，并成为工业界和学术界的研究热点[1].多变量统计过程监视的本质是将过程数据压缩以提取出有用的信息用于故障检测和诊断.以PCA和PLS为代表的多元统计方法在过程监视中受到了广泛关注，通过构造统计量即可实现对生产过程的在线监视.由PCA和PLS拓展出来的一些算法也取得了一定的发展[2-4].

随着化工过程日趋复杂化，化工连续生产过程的非线性特征越来越显著，使得当今对故障检测技术的要求越来越高.因此如何通过算法挖掘数据的高维非线性结构，提取原始数据中更多有用的信息，成为故障诊断研究的一个重要方面.为了提取数据的非线性特征，运用核技巧或核函数技术，将传统的线性技术进行核化.邓晓刚等[5]提出一种基于KPCA的非线性故障诊断方法.MENG Yafeng等[6]提出一种基于核PCA的模糊支持向量机算法，并将其成功应用于雷达发射信号的分类中.许洁等[7]将核主元分析和多重核学习支持向量机算法相结合，提出一种基于KPCA和MKL-SVM的非线性过程监控与故障诊断算法，提高了故障检测和故障诊断的速度.ZHAO Xiaoqiang等[8]提出了一种改进的FVS-KPCA用于TE过程的故障检测算法，降低了运算复杂度，提高了故障检测性能.但是这些算法在对TE过程数据进行特征映射时都是全局投影，丢失了数据的局部拓扑结构信息.

近几年，作为一种新的线性降维算法，局部保持投影(Locality Preserving Projections，LPP)被提出用来挖掘潜在的数据流形结构[9].LPP的基本思路是找到一个最优投影方向从而使在这个方向上的投影能保留原始数据的近邻结构.LPP秉承了数据局部结构保持的特点，已被成功应用于间歇过程的故障诊断中[10].值得注意的是，LPP所获取的投影向量是非正交的，因而增加了数据误差重构方面的难度.CAI Deng等[11]又提出正交局部保持投影(Orthogonal Locality Preserving Projections，OLPP)，在LPP的基础上增加一个正交化的约束条件，通过迭代计算得到相互正交的投影方向.经实验验证，OLPP比LPP具有更好的局部保持特性.

MIAO Aimin等[12]尝试将核函数技术和正交邻域保持嵌入技术相结合运用到连续过程中进行统计过程监视，算法显示出一定的优越性.本文尝试将核函数技术和投影向量间正交性原理融入局部保持投影算法中，提出了一种新的核正交局部保持投影(Kernel Orthogonal Locality Preserving Projections，KOLPP)用于工业统计过程故障诊断的非线性算法.

1 核正交局部保持投影算法

通常，输入空间的非线性数据在高维非线性投影之后很可能被线性可分.针对这种情况，借用核函数技术来拓展OLPP算法，称之为KOLPP.在KOLPP算法中，原始数据被投影到高维特征空间后，新的数据集具有线性关系并且易于计算处理，即KOLPP算法能够获取线性算法OLPP丢失的非线性结构.

KOLPP是以LPP为基础的，因此，引入LPP代价函数，在这个代价函数中引入线性变换矩阵，得到非线性特征.利用满足Mercer定理的核函数隐式在高维特征空间求解.

设输入训练样本集X={xi},i=1,2,…,N,X∈Rm×N.KOLPP算法如下：

(1) 选择非线性映射φ:Rm→F，将输入空间Rm映射到高维特征空间F，得到φ：φ(X)=[φ(x1),φ(x2),…,φ(xN)]，从而在特征空间进行Y=ATφ(X)的降维变换，将他们映射为l(l≪N)维空间中的新样本数据点，其中A=[a1,a2,…,al].因为A是由φ：φ(X)=[φ(x1),φ(x2),…,φ(xN)]张成的，因此存在一组系数a，使得

(1)

LPP代价函数可以转化成：

2ATφ(X)Lφ(X)A

(2)

其中

(3)

通过代入(1)和K(xi,xj)=〈φ(xi),φ(xj)〉可以得到：

(4)

(2) 考虑约束条件：aTKDKa=1，其中a是向量，K和D是矩阵.a与a1都表示的是向量.向量a可以取不同的值.核空间LPP可以转化成求解如下广义方程的最小特征值所对应的特征向量：

KLKTa=λKDKTa

(5)

其中：D是对角矩阵；L是拉普拉斯矩阵，L=D-W,Dii=∑jWij.

(6)

(3) 计算正交基函数，正交基为A=[a1,a2,…,al]，令A(l-1)=[a1,a2，…,al-1]，Γ(l-1)=[A(l-1)]T(KDKT)-1A(l-1).

① 取正交基矩阵A的一个向量，其中a1是矩阵A中的一个向量.a1由广义特征方程KLKTa=λKDKTa的最小特征值所对应的特征向量得到：

(7)

② KOLPP的第l个特征值对应的特征向量al由式(8)得到：

alTKDKTal=1

(8)

利用Lagrange乘数，以上最小化问题可以转化为如下方程：

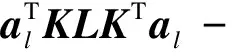
(9)

通过求解以上方程，al为以下方程的最小特征值对应的特征向量求得：

{I-(XDXT)-1A(l-1)[Γ(l-1)]-1·

[A(l-1)]Τ}(KDKT)-1KLKTal=λal

(10)

(4)对于输入样本X：φ(xi)→yi=ATφ(xi)，其中A=[a1,a2…,al].

2 基于核正交局部保持投影的故障诊断

基于KOLPP的离线建模过程如下：

(4) 利用训练集计算Q统计量.

(5) 采用KDE确定Q统计量的控制限.

基于KOLPP的在线检测和诊断过程如下：

(1) 对新来样本数据Xnew，根据训练集的均值和方差进行标准化.

(4) 计算待测样本的Q统计量.

(5) 比较待测样本的Q统计量与控制限，判断统计量是否超出控制限.

(6) 计算出每个过程变量对Q统计量的贡献，绘成直方图可以得到该统计量的贡献图.在第n个采样时刻，第i个样本的变量j对Q的贡献为：

(11)

根据贡献率的高低判断哪个变量发生了故障.

3 仿真结果与分析

3.1 TE过程

Eastman 化学公司开发的Tennessee Esatman(田纳西-伊斯曼过程)过程模拟器提供了一个实际的工业过程仿真平台，近年来已经被广泛用于验证各种故障检测与诊断方法，现已成为一种国际上通用的标准仿真模型[13-16].这个过程模型首先是以FORTRAN源代码的形式提供给过程控制学术界，主要描述了装置、物料和能量之间的非线性关系.TE过程包括5个主要操作单元、4种气体进料、2个气液放热反应生成的2种主产品、2个衍生放热反应生成的2种副产品等，过程机理复杂性极高，变量较多.具体模型流程如图1所示.

TE过程在仿真数据集中包含了所有41个测量变量和11个控制变量(不包含反应器的搅拌速度)，总共有52个观测变量.TE过程数据包含正常状态和21种不同的故障状态，每种状态分为训练数据和测试数据两部分.训练数据为480个样本，而测试数据为960个样本.在故障测试数据中，每3 min采样1次，过程仿真时间为48 h，故障出现在第9 h开始的时候，即从第161个采样时刻开始引入故障.

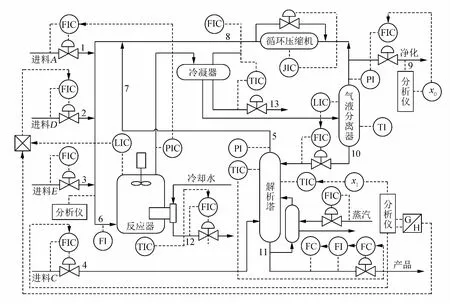
图1 TE过程工艺流程

3.2 仿真结果与分析

将核正交局部保持投影应用到TE过程中，并与KPCA和OLPP算法进行比较.3种算法潜变量的个数都选择为20个，KOLPP和KPCA的核参数β为3 500.本文选取TE数据的故障1、2、7和14来验证算法的有效性.

图2～图5分别为故障1、2、7和14的检测图.图中的虚线和实线分别对应Q统计量95 %和99 %的控制限.

图2 故障1的检测图

图3 故障2的检测图

从图2～图5可知，前150个时刻KPCA算法都有明显的超过控制限的情况，说明KPCA算法的误报率最高.在图2、图3和图4中OLPP算法也有一定的误报率.KOLPP算法在前150个时刻基本没有超过控制限的情况.

3种算法的具体检测结果如表1所示.运用误报率、漏报率及2个指标的和(错误率)来衡量算法的好坏，3种指标分别用FA、MA和ER表示.

图4 故障7的检测图

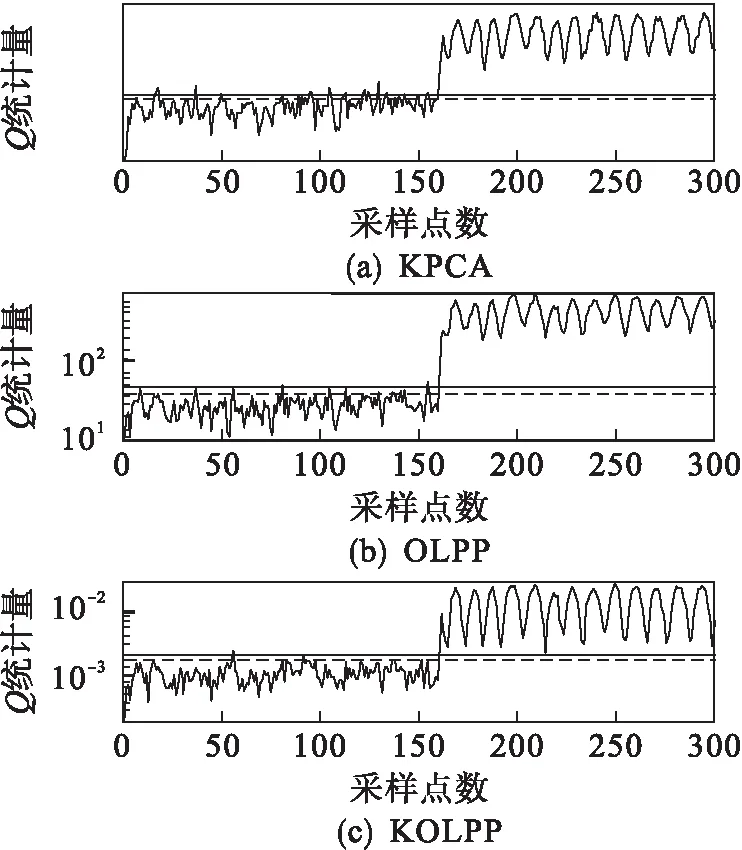
图5 故障14的检测图

表1 3种算法的故障检测结果

由表1可以看出：对4个故障进行检测，KOLPP算法能保证在最低的误报率下，有较好的检测效果.与KPCA、OLPP算法相比，KOLPP的错误率指标ER最低，故障检测效果最好，验证了该算法的有效性.

运用KOLPP算法，计算4种故障在第161个采样时刻Q统计量的贡献率，如图6所示，根据贡献率的高低判断哪个变量发生了故障.从图6可以看出，引起4种故障的主要变量分别是变量21、变量13、变量4和变量51.

表2是在Matlab7.1平台下KPCA、OLPP和KOLPP 3种算法故障检测所需的CPU时间(CPU：Pentium Dual-core 2.93 GHz RAM:1.96 GB).由表2可以看出：OLPP算法运行时间最短，这是由于OLPP是线性算法.KPCA和KOLPP算法的运行时间较长，因为测试样本在向低维空间上投影时，需要计算核矩阵.本文算法在错误率较低的情况下，运行时间相对较短.

图6 各故障的Q统计量贡献图

表2 3种算法Q统计量故障检测的CPU时间对比

4 结束语

提出一种基于核正交局部保持投影的连续过程故障诊断算法.利用核函数技术将其投影到高维的非线性空间中，提取工业过程数据中的非线性信息.在保证投影矩阵中各向量正交的同时，通过局部保持投影算法进行线性映射.最后，将KOLPP算法用于工业过程的统计监视.TE过程的仿真结果表明，该算法在错误率较低的情况下，运行时间相对较短.

[1] 周东华,李钢,李元.数据驱动的工业过程故障诊断技术：基于主元分析与偏最小二乘的方法[M].北京:科学出版社,2011:1-76.

[2] LI Y,ZHANG X M.Diffusion Maps Basedk-nearest-neighbor Rule Technique for Semiconductor Manufacturing Process Fault Detection[J].Chemometrics and Intelligent Laboratory Systems,2014,136:47-57.

[3] 郭金玉,齐蕾蕾,李元.基于DMOLPP的间歇过程在线故障检测[J].仪器仪表学报,2015,36(1):134-142.

[4] 郭小萍,李婷,李元.基于鲁棒测地线距离的复杂间歇过程故障检测[J].仪器仪表学报,2014,35(12):2681-2689.

[5] 邓晓刚,田学民.一种基于KPCA的非线性故障诊断方法[J].山东大学学报(工学版),2005，35(3):103-106.

[6] MENG Y F,REN M Q,Cai J Y,et al.Research on Radar Emitters Classification with Fuzzy Support Vector Machines[C]//IEEE.Proceedings of the International Forum on Information Technology and Applications.Washing,DC:IEEE Computer Society,2009:161-164.

[7] 许洁,胡寿松.基于KPCA和MKL-SVM的非线性过程监控与故障诊断[J].仪器仪表学报,2010,31(11):2428-2433.

[8] ZHAO X Q,WANG X M,YANG W,et al.An Improved FVS-KPCA Method of Fault Detection on TE Process[C]//IEEE.2012 Third International Conference on Digital Manufacturing and Automation.Washing,DC:IEEE Computer Society,2012:186-189.

[9] HE X F,NIYOGI P.Locality Preserving Projections(LPP)[J].Advances in Neural Information Processing Systems,2002,16(1):186-197.

[10] HU K L,YANG J Q.Multivariate Statistical Process Control Based on Multiway Locality Preserving Projections[J].Journal of Process Control,2008,18(7/8):797-807.

[11] CAI D,HE X,HAN J,et al.Orthogonal Laplacianfaces for Face Recognition[J].IEEE Transactions on Image Processing,2006,15(11):3608-3614.

[12] MIAO A M,SONG Z H,WEN Q J,et al.Process Monitoring Based on Generalized Orthogonal Neighborhood Preserving Embedding[J].IFAC Proceedings Volumes,2012,45(15):148-153.

[13] DOWNS J J,VOGEL E F.A Plant-Wide Industrial Process Control Problem[J].Computers and Chemical Engineering,1993,17(3):245-255.

[14] MCAVOY T J,YE N.Base Control for the Tennessee Eastman Problem[J].Computers and Chemical Engineering,1994,18(5):383-413.

[15] LEE G,HAN C H,YOON E S.Multiple-Fault Diagnosis of the Tennessee Eastman Process Based on System Decomposition and Dynamic PLS[J].Industrial and Engineering Chemistry Research,2004,43(25):8037-8048.

[16] YIN S,DING S X,HAGHANI A,et al.A Comparison Study of Basic Data-Driven Fault Diagnosis and Process Monitoring Methods on the Benchmark Tennessee Eastman Process[J].Journal of Process Control,2012,22(9):1567-1581.