数形结合思想在三角函数教学中的运用

江苏省射阳县高级中学 王翠霞

由于三角函数具有抽象性的特点，学生往往学习起来会感到比较困难，因此，要想让学生能比较轻松地学习三角函数，让学生对三角函数的知识点有直观的认识是关键。数形结合可以将抽象的数学问题更加直观地展示出来，因此通过运用“数形结合”的思想，可以很好地帮助学生学习三角函数。本文将浅谈数形结合在三角函数中的应用。

一、利用图象，记牢函数性质

在整个函数学习中，由于三角函数的函数性质主要有定义域、值域、周期性、单调性和奇偶性，内容较多，学生们对三角函数的一些知识点不能记牢，而三角函数的函数性质是历年考试的重点。为了克服这些困难，可以利用图象，运用数形结合的思想，记牢函数性质。

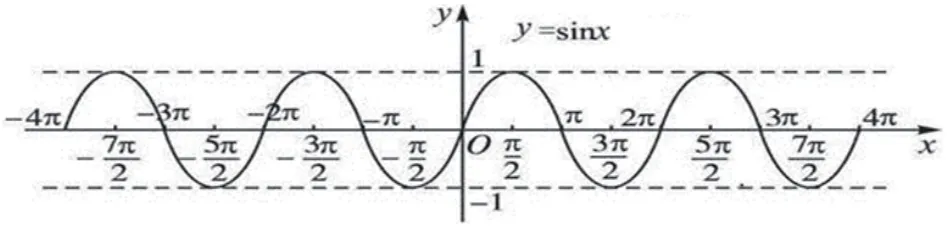
为1，最小值为-1，图象在[-1,1]之间，因此可以确定其值域为[-1,1]。图象在上是一样的，这就可以推断出其为周期函数，而周期为图象整体有增有减，是没有单调性的,但是细看图象在上是单调递增的，在上是单调递减的，因此我们可以从中发现规律，推出其单调增区间为单调减区间为其图象关于原点对称，因此可以得出该函数是奇函数。通过函数图象，我们可以更加生动、直观地看出并得到其函数性质。

二、利用图象，确定函数值正负

许多三角函数的题目需要确定函数值的正负，而且函数值的正负确定是解决一个题目的基础。许多同学在做题目的时候经常不能很清楚地确定函数值的正负，其实出现这些问题的原因有二:一是学生在演算时由于粗心大意而出现的失误，二是学生根本就不知道怎么确定函数值的正负。其实以上两种原因都可以通过画出函数图象来解决。

利用函数图象，我们只需把自变量的范围在图象上标注出来，即可确定函数值的正负，这样不仅可以避免学生在演算时由于粗心大意而出现失误，而且能更直观地向学生们展示如何确定正负号。

三、利用图象，比较函数值大小

学生在做题时经常会遇到这样一类题目：给出角度的范围，比较三角函数值大小。可能有些学生在解答的时候会带入特殊值，从而比较函数值的大小，其实运用特值的思想是可以的，但是其实这并不是出题者的本意，而且有些题目是无法用特值来解答的。当遇到比较函数值大小的题目时，画出图象，利用数形结合的思想，才是出题者的意图和解答本类题目的关键。

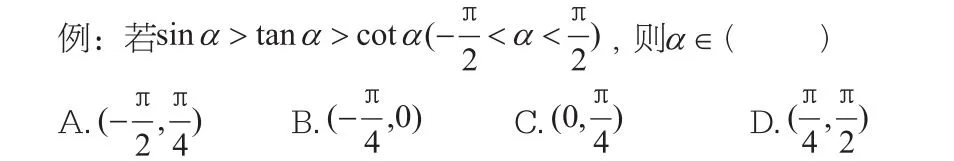
解析：可能许多学生拿到这个题目的时候，就不知道怎么去做了，因为不能用特值了。其实本题目运用到了数形结合的思想，通过画出单位圆来进行解题。从已知条件：再根据的函数性质，可以得出再根据可以得画出图形，可以得出,从而确定是

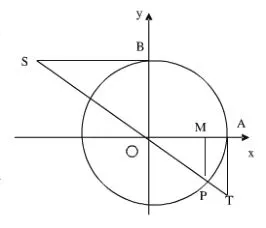
如果单纯从数出发，不仅比较抽象，难以让人理解，而且会容易引起计算的错误。通过运用数形结合的思想画出图象，可以快速地将题目解答出来，不仅条理清晰，而且可以避免对函数值的正负判断错误。

综上所述，通过运用数形结合的思想画出函数图象，可以将抽象的三角函数问题转化成比较直观的几何图形，这样不仅可以帮助学生更容易地学习三角函数，还可以激发学生的学习兴趣。