探究方法 寻求规律 发掘背景——记一道解析几何题的讲评

江苏省常熟中学 朱 震

在一次复习解析几何的单元测试中有一道题目，学生的答题情况不尽人意。在讲评课上，笔者带领学生共同探讨了其解答方法。

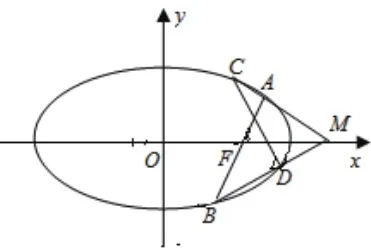
一、原题呈现

思路一：C随A动，D随B动，所以CD的斜率必与AB有关。因此可以考虑用A、B两点坐标表示C、D两点坐标，进而用k来表示CD的斜率k1。

解：直线AM方程为：与椭圆方程联立消去y整理得该方程的两个根为

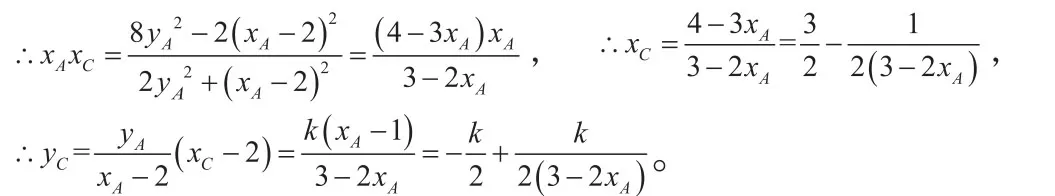
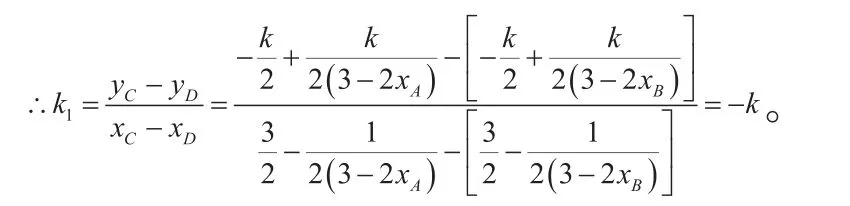
这是大多数解出此题的学生使用的方法。想法自然，处理得当。

二、探究方法

笔者在批阅时还发现了如下思路，在课上与同学们探究。

思路二：类比抛物线问题，用弦的端点坐标来表示弦所在直线方程。

∴直线AB方程为：

∵AB过F（1,0）

学生做到这里卡住了，放弃了用这一思路进行下去。笔者鼓励全体学生一起思考，看看能不能帮她一起走出来。

学生集思广益，很快得到了一个可行的方案：消元！

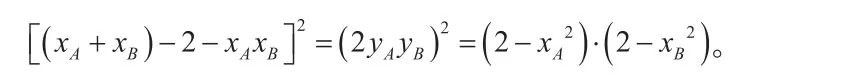
整理得：

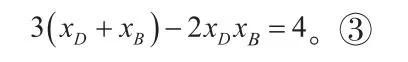
由①②得 ，由①③得 。

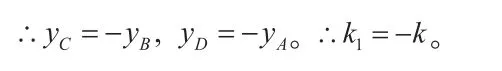
笔者：H同学尝试将研究抛物线的常用方法迁移到椭圆中，做法很好。虽然这样的迁移不一定简单，甚至不一定有效，但这是我们研究问题的常用策略。下面请同学们一起看一下使用这一思路得到的结果，我们能发现什么？

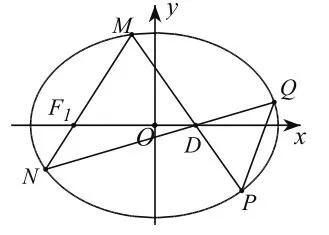
学生：点A与点D，点B和点C都关于x轴对称，所以CD应该也经过F点，题目所给的图画错了。

笔者：对的！如果图画对了（如图），大家就容易猜到答案了。除了看到图画错了，我们还能发现什么呢？

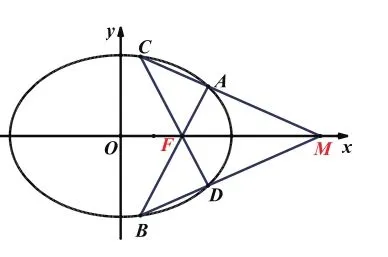
学生：①②③式的形式一样，都是对称式。但是①式是通过AB经过F点得到的，②③式是通过直线经过M点得到的，居然会有相同的结果。

笔者：然后呢？是不是只要通过x轴上一定点，就会有这样的结果？还是这两点必须满足某种关系，才会有相同的结果？

学生：必须满足某种关系！根据我的经验，我猜是：横坐标之积为2。

笔者：那好，我们一起来验证一下你的这个猜想。

三、寻求规律

为了得到对称式，学生很快给出了如下解答：

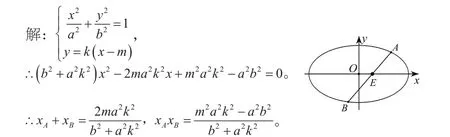
设存在常数λ，使得对任意满足条件的k，恒为常数，

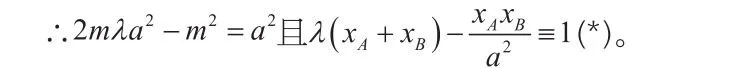
∴点E的横坐标为方程的根。

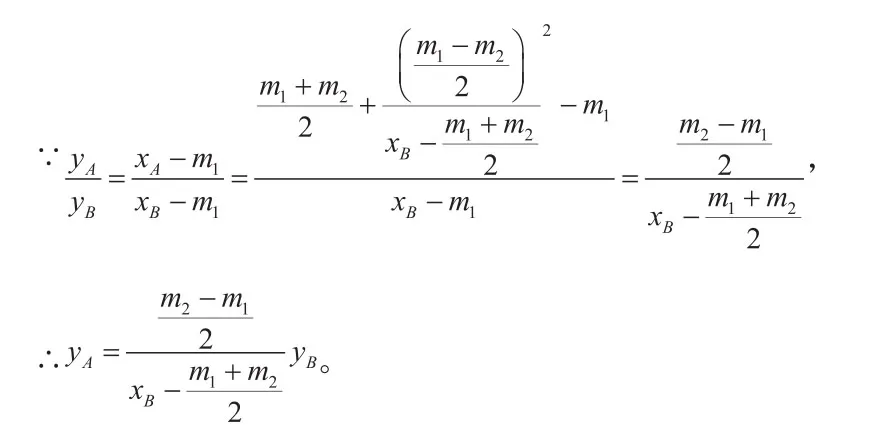
笔者：猜想正确！如果在解题之前我们就知道这一结论，就可以直接联立椭圆和直线方程，用韦达定理凑得两交点横坐标之间的关系，从而简化运算。下面我们再一起来看看能不能得到更有价值的结论。

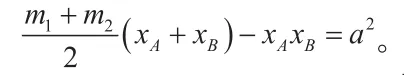
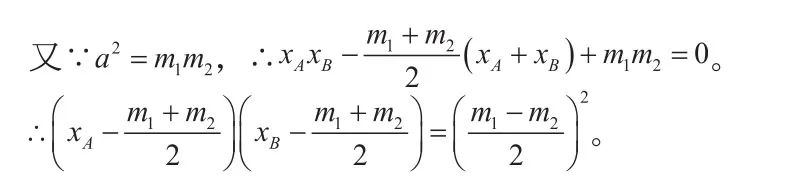
这样，原题中两交点的横坐标之间的关系就明确了！

笔者：那么两交点的纵坐标之间有何关系呢？

记E点对应的m为，则：

接着，笔者找出如下习题，供学生练习。

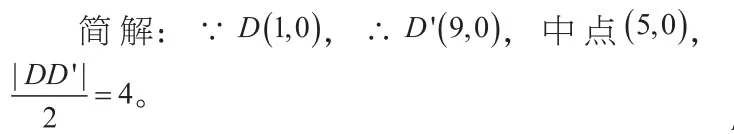
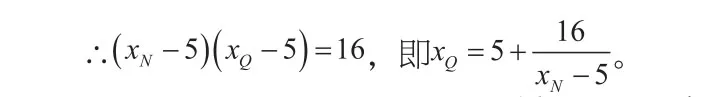
通过上述探究过程，我们得到一个一般性规律，即：若经过x轴上一定点的直线与椭圆交于A、B两点，则有：

①A、B两点的横坐标之间满足：

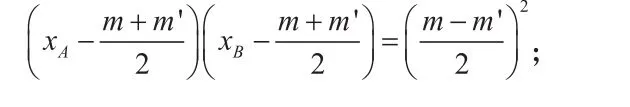
②A、B两点的横坐标之间满足：其中，

而得到上述规律的常用方法，就是韦达定理结合待定系数法。今后我们在遇到类似条件时，就可以有的放矢。

四、发掘背景

笔者感到上述结论是优美的，似乎存在着某种必然的联系。课后，笔者继续深挖，在圆中挖掘本题的背景。

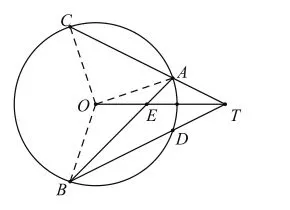
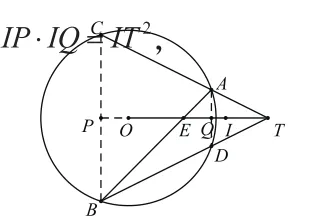
如图，点E是半径为R的圆O内一点，点T在射线OE上，满足过E的直线交圆O于A、B两点，TA、TB分别交圆O于点C、D。求证AD⊥OE，BC⊥OE。

同理，∠OBE=∠OTB。

另外，由BC⊥OE且AD⊥OE可得AD∥BC，

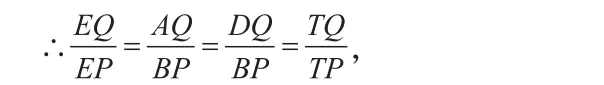
如图，取ET中点I，由调和点列相关性质得

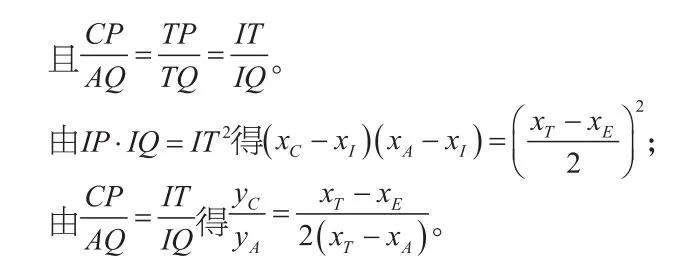
椭圆可以由圆经过伸压变换得到，而伸压变换保持同一直线上各线段比例关系不变，将上述圆进行纵向伸压得到椭圆之后，水平直径所在直线上各线段比例关系不变。

五、反思总结

波利亚指出：“教师最重要的任务之一是帮助他的学生。这个任务并不容易，它需要时间、实践、奉献和正确的原则。学生应当获得尽可能多的独立工作经验。但是，如果把问题留给他一人而不给他任何帮助，或者帮助不足，那么他可能根本得不到提高。而如果教师的帮助太多，就没有什么工作留给学生了。”数学教师几乎每天都要批改作业，常常会在学生的作业中看到不同的解法，有些学生能够顺利解出答案，有些学生会卡在某一步。我们不能仅满足于判断学生作业的对错，更应花时间帮助卡住的同学走出来，这个任务也不容易，也需要时间、实践、奉献和正确的原则。对于使用特殊方法而不成功的学生，应给予个别辅导，指出学生错误之处，引导学生深入思考，帮助学生规避弯路。对于有价值的方法，可带领全班同学共同探究，进行推广，做到举一反三，多题一解。

教师常比学生有更敏锐的洞察力，比学生有更多的时间进行钻研，当我们发现某一规律时，常可寻其背景，这是下一步命题的源泉。笔者根据上述背景进一步研究，命制了一系列新的习题，在苏州市高中数学命题研究会议上，作了题为《推陈出新之心路历程》的报告，获得了一致好评。