向量组线性相关性解题方法探究

贺电鹏

(郑州工商学院 公共基础课教学部,河南 郑州 451400)

向量组线性相关性解题方法探究

贺电鹏

(郑州工商学院 公共基础课教学部,河南 郑州 451400)

在解决向量组的线性相关性的问题时，方法的选择是一个必然的过程，不同的题目选择最优的解决方案，会使得解题达到事半功倍的效果.理清思路，抓住重点，总结出解决向量组线性相关性题目的多种方法，可以更深地认识向量组的线性相关性，解决该类问题的难点.

向量组；线性相关；线性无关；矩阵；秩；数学归纳法

1 向量组线性相关性的地位和作用

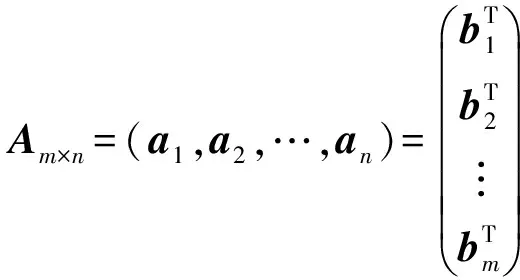
基于向量组的线性相关性的特殊和重要的地位，研究向量组的线性相关性的解题方法就显得尤为重要，向量组的线性相关性的解题策略可以帮助我们更好地理解向量组线性相关性的内涵，更好地使用线性相关性学习其他知识，解决其他问题.本文结合不同的题型，尽可能多的给出各种向量组线性相关和线性无关的解题方法，力求在在向量组的线性相关性解题方法上做一个尽可能完整的总结.

2 向量组线性相关性解法研究

2.1 定义法

定义1[2]给定向量组A:a1,a2,…,am，如果存在不全为零的数k1,k2,…,km，使k1a1+k2a2+…+kmam=0,则称向量组A是线性相关的，否则称它线性无关.

说明定义1中的“否则称它线性无关”，即若当且仅当k1=k2=…=km=0时，k1a1+k2a2+…+kmam=0才成立，则称向量组A:a1,a2,…,am线性无关.

例1[2]已知向量组a1,a2,a3线性无关，b1=a1+a2,b2=2a2+3a3,b3=5a1+3a2，试证向量组b1,b2,b3线性无关.

证明设有x1,x2,x3，使x1b1+x2b2+x3b3=0，即x1(a1+a2)+x2(2a2+3a3)+x3(5a1+3a2)=0，亦即(x1+5x3)a1+(2x2+3x3)a2+3x2a3=0，因a1,a2,a3线性无关，故有

解得方程组只有零解x1=x2=x3=0，所以，由定义1可知，向量组b1,b2,b3线性无关.

例2[2]设b1=a1+a2,b2=a2+a3,b3=a3+a4,b4=a4+a1，试证向量组b1,b2,b3,b4线性相关.

证明取k1=1,k2=-1,k3=1,k4=-1，则k1,k2,k3,k4不全为零，且k1b1+k2b2+k3b3+k4b4=b1-b2+b3-b4=(a1+a2)-(a2+a3)+(a3+a4)-(a4+a1)=0,因此，由定义1可知，向量组b1,b2,b3,b4线性相关.

2.2 定义的等价命题法

2.2.1 等价命题一[2]

设向量组A:a1,a2,…,am构成矩阵A=(a1,a2,…,am)，则由定义1知，判断向量组A:a1,a2,…,am线性相关性只需要判断表达式k1a1+k2a2+…+kmam=0的系数k1,k2,…,km全为零和不全为零即可，即有如下等价命题.

1)向量组A:a1,a2,…,am线性相关⟺齐次线性方程组Ax=0有非零解；

2)向量组A:a1,a2,…,am线性无关⟺齐次线性方程组Ax=0只有零解.

例3已知向量组a1,a2,a3线性无关，b1=a1+2a2+3a3,b2=2a1+2a2+4a3,b3=3a1+a2+3a3，试证向量组b1,b2,b3线性无关.

2.2.2 矩阵的秩法

定理1[2]向量组A:a1,a2,…,am线性相关的充分必要条件是它所构成的矩阵A=(a1,a2,…,am)的秩小于向量个数m；向量组A线性无关的充分必要条件是R(A)=m.

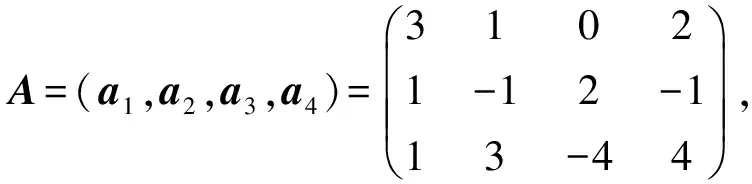
说明当向量组的维数小于向量组的向量个数时，向量组一定线性相关.

例5前面例3还可以依据矩阵的秩法进行证明.

2.3 向量组等价法

定理2[2]向量组A:a1,a2,…,am与向量组B:b1,b2,…,bl等价的充分必要条件是R(A)=R(B)=R(A,B)，其中A和B是向量组A和B所构成的矩阵.

说明①当m=l时，向量组A和B同时线性相关或线性无关;②当ml时，若向量组A线性无关，则向量组B也线性无关.

例6同前面例1.

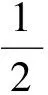
2.4 反证法[3]

反证法是数学中常用的证明方法，即先假设命题的否命题为真，推出结果与已知矛盾，从而原命题成立.反证法可以给我们提供另外一种说明线性相关性的思路.

例7设b1=a1,b2=a1+a2,…,br=a1+a2+…+ar且向量组a1,a2,…,ar线性无关，证明向量组b1,b2,…,br线性无关.

例8[4]证明：若向量组a1+a2,a2+a3,a3+a1线性无关，则必有向量组a1,a2,a3线性无关.

证明(用反证法)假设a1,a2,a3线性相关，则R(a1,a2,a3)≤2，由于a1+a2,a2+a3,a3+a1可由a1,a2,a3线性表出，则R(a1+a2,a2+a3,a3+a1)≤2，由此得到向量组a1+a2,a2+a3,a3+a1线性相关，这与题设向量组a1+a2,a2+a3,a3+a1线性无关矛盾，故必有向量组a1,a2,a3线性无关.

2.5 数学归纳法

第一数学归纳法设P(n)是关于自然数n的命题，若①P(n)在n=1时成立；②在P(k)(k是任意自然数)成立的假定下，可以推出P(k+1)成立，则P(n)对一切自然数n都成立.

第二数学归纳法设P(n)是关于自然数n的命题，若①P(n)在n=1时成立；②在P(k)(1≤n≤k,其中k是任意自然数)成立的假定下，可以推出P(k+1)成立，则P(n) 对一切自然数n都成立.

例9[5]设线性无关的向量组

a1,a2,…,am

(1)

可由向量组

b1,b2,…,bt

(2)

线性表示，且m≤t. 则可从(2)中选出(t-m)个向量组成的向量组bj1,bj2,…,bj(t-m)，使得向量组a1,a2,…,am,bj1,bj2,…,bj(t-m)与向量组(2)等价.

证明用第一数学归纳法证明.

因此，当m=s时，即s≤t，向量组a1,a2,…,as-1,as,bj,s+1,…,bj,t与向量组(2)等价. 于是，由数学归纳法可知，结论得证.

向量组的线性相关性，在线性代数的知识点的联结上有至关重要的作用. 求解向量组的线性相关性有很多种方法，很多问题会出现一道题目多种解法，但往往是殊途同归，都能达到证明向量组线性相关性的目的. 在学习向量组的线性相关性的时候，应该及时总结，分析各个知识点的联系，达到多种方法融会贯通，深层次理解向量组线性相关性的概念.

[1] 彭司萍,龙正平.线性代数教学主线研究[J].高师理科学刊,2016,36(6):75-79.

[2] 同济大学数学系.线性代数[M].6版.北京:高等教育出版社,2014:81-96.

[3] 朱宝骧,郭金勇.反证法在高等代数中的应用[J].柳州师专学报,2015,30(3):110-112.

[4] 钱志强.最新线性代数教与学参考[M].北京:中国致公出版社,2001:309-341.

[5] 栾召平.证明向量组线性相关性的几种方法[J].山东电大学报,2002(2):61-62.

ResearchonSolutionofLinearCorrelationofVectorGroup

HE Dianpeng

(DepartmentofGeneralEducation,ZhengzhouTechnologyandBusinessUniversity,Zhengzhou451400,China)

In solving the problem of linear correlation of vector groups, the choice of method is a necessary process. Choosing the best solution will make linear correlation problems much easier. It is possible to understand the linear correlation of vector groups and solve the problem by clearing thinking, grasping key points, and summarizing the various methods of the problem.

vector groups; linear correlation; linear independence; matrix; rank; mathematical induction

2017-05-03

郑州工商学院教育教学改革研究重点项目“应用型民办本科高校数学课程体系改革的研究与实践” (GSJG2017005)成果之一

贺电鹏(1988—)，男，河南郑州人，郑州工商学院公共基础教学部讲师.

10.3969/j.issn.1007-0834.2017.04.012

O151.24

A

1007-0834(2017)04-0051-04