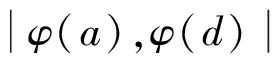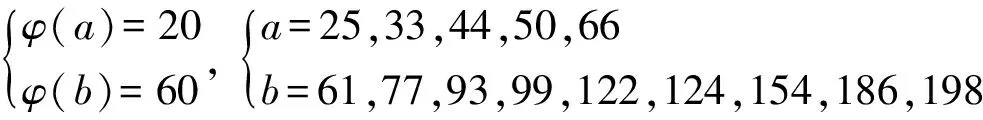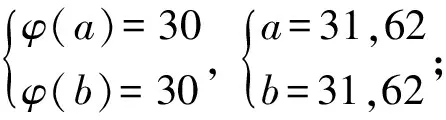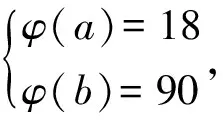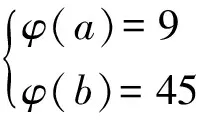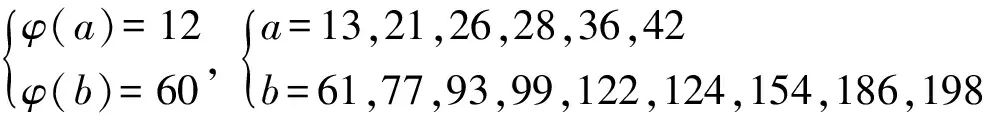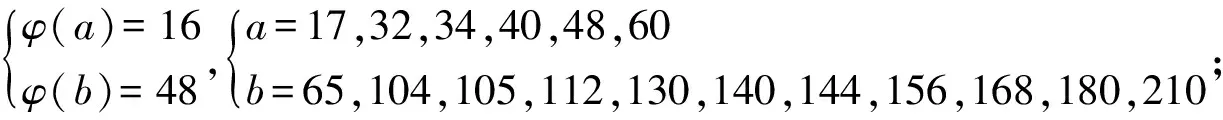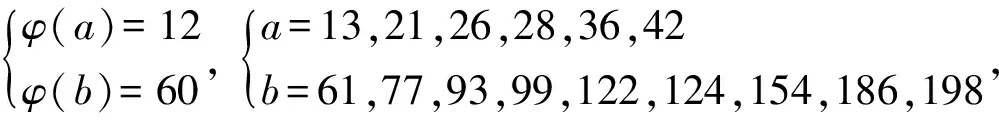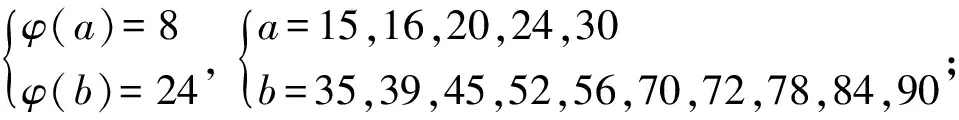欧拉函数方程φ(ab)=15(φ(a)+φ(b))的正整数解
袁合才, 宋倩倩, 贾媛媛
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
欧拉函数方程φ(ab)=15(φ(a)+φ(b))的正整数解
袁合才, 宋倩倩, 贾媛媛
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
讨论了欧拉函数方程φ(ab)=15(φ(a)+φ(b)),其中a,b为不小于2的正整数.利用初等数论方法,得到该方程所有234组正整数解.
欧拉函数;丢番图方程;正整数解
设φ(n)为欧拉函数,其值为在1,2,…,n-1中与n互素的正整数的个数.近年来,含有欧拉函数φ(n)的丢番图方程吸引了国内外越来越多学者的关注.1960年,MAKOWSKI[1]研究了方程φ(m+k)=φ(m)+φ(k),得出结论:对于任意k,方程φ(m+k)=2φ(n)至少有一个解;BROWKIN[1]证明了若k=3,则方程φ(m+k)=φ(m)+φ(k)没有正整数解x<37 182 142.2000年EL-KASSAR[2]研究了方程kφ(n)=φ(n+1)及方程kφ(n+1)=φ(n)的整数解.对于欧拉函数方程φ(ab)=k(φ(a)+φ(b)),2010年孙翠芳等[3]研究了当k为素数时方程的可解性问题,给出了当k=2时该方程的全部正整数解;最近,文献[4-9]分别得到了当k=4,5,6,7,8,9时该方程的全部正整数解.本文将研究欧拉函数方程φ(ab)=k(φ(a)+φ(b))当k=15时的可解性问题,利用初等数论方法给出了该方程的所有正整数解.
1 若干引理
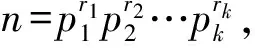

引理3当n≥2时,有φ(n) 定理1欧拉函数方程φ(ab)=15(φ(a)+φ(b))共有234组正整数解,即为下述正整数解及其对称形式: (17,241),(17,287),(17,305),(17,325),(17,369),(17,385),(17,429),(17,465),(17,482), (17,488),(17,495),(17,496),(17,525),(17,572),(17,574),(17,610),(17,616),(17,620), (17,650),(17,700),(17,732),(17,744),(17,770),(17,792),(17,858),(17,900),(17,924), (17,930),(17,990),(17,1 050),(32,241),(32,287),(32,305),(32,325),(32,369),(32,385), (32,429),(32,465),(32,495),(32,525),(34,241),(34,287),(34,305),(34,369),(34,385), (34,429),(34,465),(34,495),(34,525),(40,241),(40,287),(40,369),(40,429),(48,241), (48,287),(48,305),(48,325),(48,385),(60,241),(60,287),(16,286),(16,310),(16,350), (16,366),(16,450),(16,462),(20,286),(20,366),(20,462),(24,286),(24,350),(30,244), (30,248),(30,286),(30,308),(22,62),(26,44),(26,50),(26,66),(28,50),(28,66), (36,50),(42,44),(42,50),(21,93),(21,99),(21,186),(21,198),(36,93),(42,93), (42,99),(16,244),(16,308),(16,372),(16,396),(20,244),(20,308),(20,372),(20,396), (20,248),(24,244),(24,308),(28,44),(36,44),(40,65),(40,105),(60,65),(60,105), (35,45),(35,90),(45,70),(16,248),(24,248),(36,99),(20,70),(20,90),(30,70). 证明考虑欧拉函数方程 φ(ab)=15(φ(a)+φ(b)), (1) φ(a)=q1φ(d),φ(b)=q2φ(d), 由引理2 (2) 由(1)、(2)式整理得 φ(ab)=15(φ(a)+φ(b))=15(q1φ(d)+q2φ(d))=dq1q2φ(d) , 即 (3) 又d=1,φ(d)=1,得 又由gcd(a,b)=d=1,可得此时方程(1)的正整数解为 (17,241),(17,287),(17,305),(17,325),(17,369),(17,385),(17,429),(17,465),(17,482), (17,488),(17,495),(17,496),(17,525),(17,572),(17,574),(17,610),(17,616),(17,620), (17,650),(17,700),(17,732),(17,744),(17,770),(17,792),(17,858),(17,900),(17,924), (17,930),(17,990),(17,1 050),(32,241),(32,287),(32,305),(32,325),(32,369),(32,385), (32,429),(32,465),(32,495),(32,525),(34,241),(34,287),(34,305),(34,369),(34,385), (34,429),(34,465),(34,495),(34,525),(40,241),(40,287),(40,369),(40,429),(48,241), (48,287),(48,305),(48,325),(48,385),(60,241),(60,287). 又d=2,φ(d)=1,得 又由gcd(a,b)=d=2,可得此时方程(1)的正整数解为 (16,286),(16,310),(16,350),(16,366),(16,450),(16,462),(20,286),(20,366),(20,462), (24,286),(24,350),(30,244),(30,248),(30,286),(30,308),(22,62),(26,44),(26,50), (26,66),(28,50),(28,66),(36,50),(42,44),(42,50). 又由 gcd(a,b)=d=3,可得此时方程(1)的正整数解(21,93),(21,99),(21,186),(21,198),(36,93),(42,93),(42,99). 又由gcd(a,b)=d=4,可得此时方程(1)的正整数解(16,244),(16,308),(16,372),(16,396),(20,244),(20,308),(20,372),(20,396),(20,248),(24,244)(24,308),(28,44),(36,44). 又由gcd(a,b)=d=5,可得此时方程(1)的正整数解(40,65),(40,105),(60,65),(60,105),(35,45),(35,90),(45,70). 又由gcd(a,b)=d=6,此时方程(1)无正整数解. 又由gcd(a,b)=d=8,此时方程(1)正整数解(16,248),(24,248). 又由gcd(a,b)=d=9,此时方程(1)正整数解(36,99). 又由gcd(a,b)=d=10,此时方程(1)正整数解(20,70),(20,90),(30,70). 又由gcd(a,b)=d=15,此时方程(1)无正整数解. 又由gcd(a,b)=d=16,此时方程(1)无正整数解. 又由gcd(a,b)=d=20,此时方程(1)无正整数解. 综合上述讨论并根据欧拉函数方程(1)的解的对称形式可知,方程(1)共有234组正整数解. [1] GUY R. Unsolved Problems in Number Theory[M].3rd ED.Beijing:Science Press,2004. [2] EL-KASSAR. On the equationskφ(n)=φ(n+1) andkφ(n+1)=φ(n)[C]//Number theory and related topics. Seoul:Yonsei University Institute of Mathematics Science, 2000:95-109. [3] 孙翠芳,程智. Some kind of equation involving Euler function[J].Journal of Mathematical Study,2010,43(4) :364-369. [4] 张四保.有关Euler函数φ(n)的方程的正整数解[J].数学的实践与认识,2014,44(20):302-305. [5] 孙树东.一个与Euler函数φ(n)有关的方程的正整数解[J].北华大学学报(自然科学版),2015,16(2):161-164. [6] 管春梅,张四保.与Euler函数φ(n)有关的方程的两个方程[J].数学的实践与认识,2016,46(9):221-225. [7] 鲁伟阳,高丽,王曦浛.有关Euler函数φ(n)的方程的可解性问题[J].江西科学,2016,34(1):15-16. [8] 郭瑞,赵西卿,张利霞,等.关于欧拉函数方程φ(mn)=3k(φ(m)+φ(n))的正整数解[J].江西科学,2016,34(2):154-157. [9] 张四保,席小忠.有关方程φ(ab)=k(φ(a)+φ(b))的正整数解[J].南京师大学报(自然科学版),2016,39(1):41-47. PositiveIntegerSolutionsofEulerFunctionEquationφ(ab)=15(φ(a)+φ(b)) YUAN Hecai, SONG Qianqian, JIA Yuanyuan (SchoolofMathematicsandStatistics,NorthChinaUniversityofWaterResourceandElectricPower,Zhengzhou450046,China) Discussed the positive integer solutions of Euler function equationφ(ab)=15(φ(a)+φ(b)), wherea,bare positive integers not less than 2. By using the method of elementary number theory, we obtained a total of 234 positive integer solutions. Euler function; Diophantine equation; positive integer solutions 2017-08-30 华北水利水电大学创新创业项目 袁合才(1978—),男,河南兰考人,华北水利水电大学数学与统计学院副教授,主要研究方向:微分方程数学建模、丢番图方程. 10.3969/j.issn.1007-0834.2017.04.001 O156 A 1007-0834(2017)04-0001-05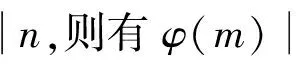
2 主要结论及其证明