河南四地区56年降水周期及空间分布研究
彭高辉, 李 斐, 杨 茜, 王金鹏
(1.华北水利水电大学 数学与统计学院,河南 郑州 450046;2.河南省水利第一工程局,河南 郑州 450000)
河南四地区56年降水周期及空间分布研究
彭高辉1, 李 斐1, 杨 茜1, 王金鹏2
(1.华北水利水电大学 数学与统计学院,河南 郑州 450046;2.河南省水利第一工程局,河南 郑州 450000)
依据河南新乡、卢氏、郑州、开封四地区1955—2010年近56年的年降水资料,采用线性倾向估计、小波分析和Z指数方法,对河南四地区趋势性、相关性、周期性及旱涝情况进行了研究.结果表明:河南四地区的空间区域降水量总体呈现西少东多、南少北多的特点;降水第一主周期趋势基本保持一致,平均周期为18 a左右,随着时间尺度的变化,区域地理差异也随着小周期的波动逐渐凸显出来.
周期性;小波分析;线性趋势分析;旱涝分析;Z指数
0 引言
降水作为影响气候变化的一个重要因素,一直受到各界广泛关注,对降水演化规律的研究也一直是水文、气象等领域的研究热点.河南省位于中国中东部、黄河中下游,地处南北气候过渡带,地形复杂,涵盖山地、丘陵、平原、盆地等多种地貌类型,降水空间分布存在差异.因此,研究河南省区域降水具有一定的现实和指导意义.
目前,国内已有不少学者对此进行了相应研究.张丽等[1]采用线性倾向估计、5 a滑动平均、Mann-Kendall突变检测、滑动t-检验等方法分析了郑州市1951—2011年降水及气温的变化特征;王跃民等[2]采用Z指数、旱涝指数、降水距平百分率方法研究旱涝等级;郝秀平等[3]采用标准降水指数方法研究河南省干旱时空演变规律.
本文依据中国气象数据共享网[4]提供的河南省新乡、卢氏、郑州、开封四地区1955—2010年年降水资料,采用线性倾向估计、Morlet小波分析和Z指数方法对新乡、卢氏、郑州、开封四地区的降水情况进行研究,旨在利用降水演化规律为农业生产提供参考,同时对研究河南省整体的气候变化有一定程度的参考意义.

表1 河南四地区经纬度及降水分布Tab.1 Four regions latitude and longitude and precipitation distribution of Henan
1 河南四地区年降水量总体分析
表1为河南四地区的经纬度坐标及1955—2010年的年均降水量,图1为依据表1中的数据绘制的河南四地区降水分布图.由图1可知,河南四地区的降水量自北向南,由西向东呈现逐渐增多趋势.以新乡作为比较对象,采用Pearson相关性分析降水量情况,结果显示与卢氏、郑州、开封的相关系数分别为0.375、0.625、0.629,表明在一定程度上降水与地理分布有一定相关性.
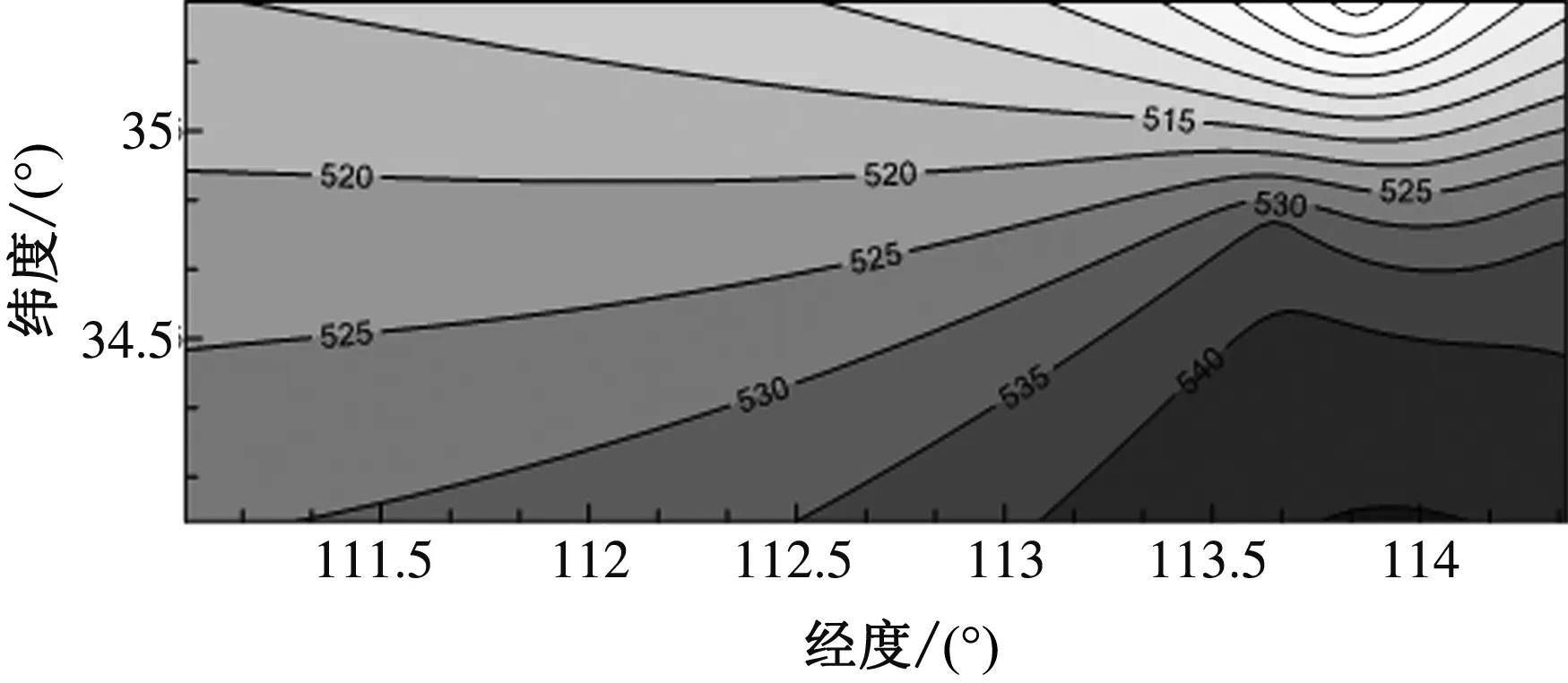
图1 河南四地区降水分布图Fig.1 Distribution of precipitation in four areas of Henan Province注:色阶颜色越深,降水量越多.
2 降水周期分析
采用Morlet小波对河南四地区的降水资料进行剖析,依次对四个地区的年均降水序列进行连续小波变换[5],通过尺度a的伸缩和时间轴b上的平移构造连续小波ψa,b(t)(a,b∈R,a≠0),得到给定函数f(t)∈L2(R)的小波变换系数Wf(a,b),揭示降水序列在不同尺度下的丰—枯变换情况;进一步将时间域上关于a的所有小波系数Wf(a,b)的平方积分,得到小波方差Var(a),确定序列的主周期;最后通过主周期趋势图判断各站点的降水周期,从而解决非平稳序列在不同时间尺度下的周期问题.
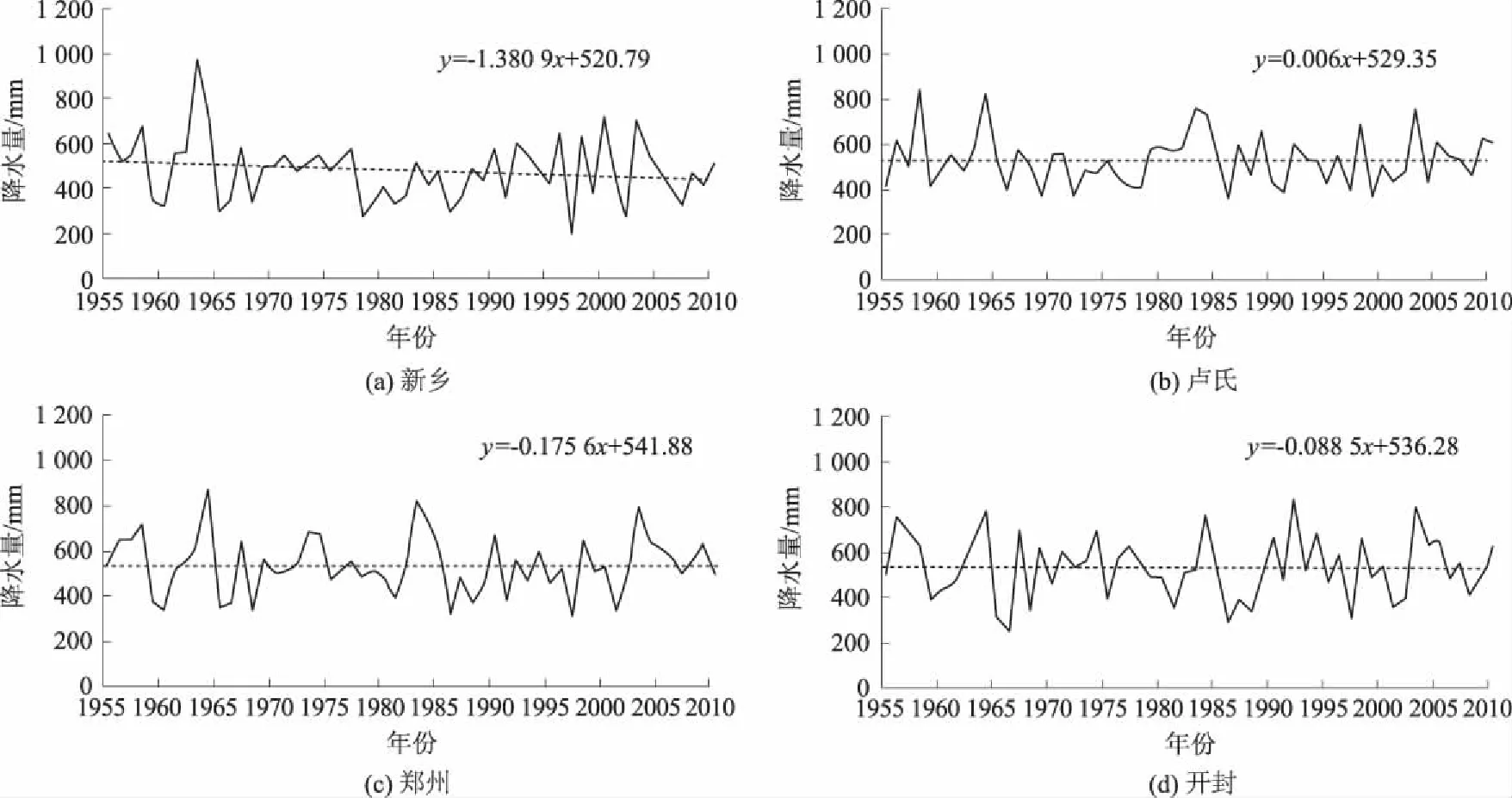
图2 河南四地区1955—2010年降水量趋势图Fig.2 Trends of precipitation from 1955 to 2010 in four areas of Henan Province
2.1 小波系数
由于小波系数实部等值线图反映降水序列不同时间尺度下的周期变化及其在相应时间域中的分布,图3为河南四地区年降水量的Morlet小波变换实部时频分布,显示不同时间尺度下降水的变化趋势,存在明显的年代和年际变化.由于不同时间尺度对应不同的降水结构,以新乡地区为例,图3(a)显示其降水序列存在较为明显的23~31 a、12~20 a、7~12 a尺度的周期震荡.在23~31 a时间尺度里,新乡年降水周期震荡非常显著,初步判断此时间尺度域存在主周期,而12~20 a和7~12 a有更多的相对多雨期和少雨期的循环交替,降水突变点增多.图3(b)~(d)的分析亦同,卢氏存在18~25 a、13~18 a、6~12 a、3~7 a的4类尺度的周期变化规律;郑州存在20~28 a、13~19 a、7~11 a、4~6 a的4类尺度的周期变化规律;开封存在25~32 a、12~18 a、8~11 a、3~7 a的4类尺度的周期变化规律.
2.2 小波方差检验
通过小波系数积分得到小波方差,根据方差[6]值越大,对应时间尺度下的周期震荡越强,检验通过小波系数分析得到的降水周期.
图4为河南四地区不同时间尺度[7]下的小波方差图.以新乡地区为例,由图4(a)知,新乡降水小波方差有3个峰值,分别对应9 a、15 a、28 a的时间尺度,其中最大峰值对应28 a时间尺度,此时周期震荡最强,为第一主周期;第二、三主周期依次对应15 a、9 a时间尺度.图4(b)~(d)的分析亦同,均存在4个峰值,分别对应不同的时间尺度,通过存在的不同周期进而调节降水在整个时间域内的变化特征.
根据小波方差结果绘制出控制降水演变的第一~三主周期趋势图如图5~7,从主周期趋势图分析不同时间尺度下降水序列中存在的平均周期及丰—枯变化.

图3 河南四地区1955—2010年降水Morlet小波变换实部时频分布Fig.3 Time-frequency distribution of precipitation Morlet wavelet transform from 1955 to 2010 in four areas of Henan Province注:图3(a)~(d)中的等值曲线为小波系数实部值.当小波系数实部值为正时,代表降水丰水期;为负时,表示降水枯水期
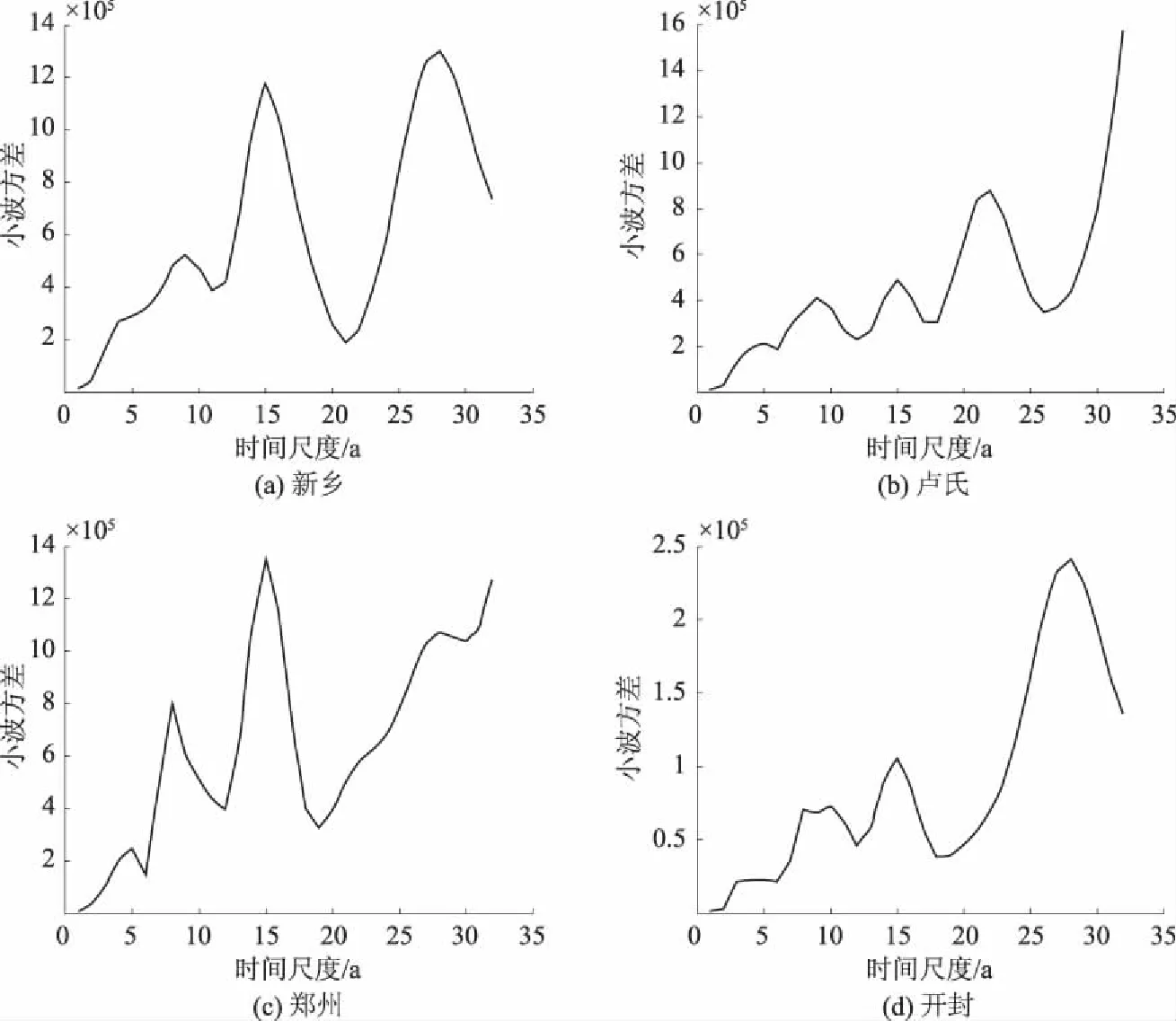
图4 河南四地区1955—2010年年均降水量序列的小波方差变化Fig.4 Wavelet variance variation of precipitation sequence from 1955 to 2010 in four areas of Henan Province注:图4(a)~(d)中横坐标为时间尺度,纵坐标为小波方差
由图5可知,河南四地区降水第一主周期趋势基本保持一致,但地理位置的差异性决定其周期变化的不同.新乡在时间尺度为28 a时的平均变化周期约为18 a,大约3.1个周期的丰—枯变化;卢氏在时间尺度为23 a时的平均变化周期约为14 a,大约4个周期的丰—枯变化;郑州在时间尺度为15 a时的平均变化周期约为10 a,大约5.6个周期的丰—枯变化;开封在时间尺度为28 a时的平均变化周期为18 a左右,大约3.1个周期的丰—枯变化.这说明在不同尺度下,流域降水的平均周期及丰—枯变化特征是不尽相同的.
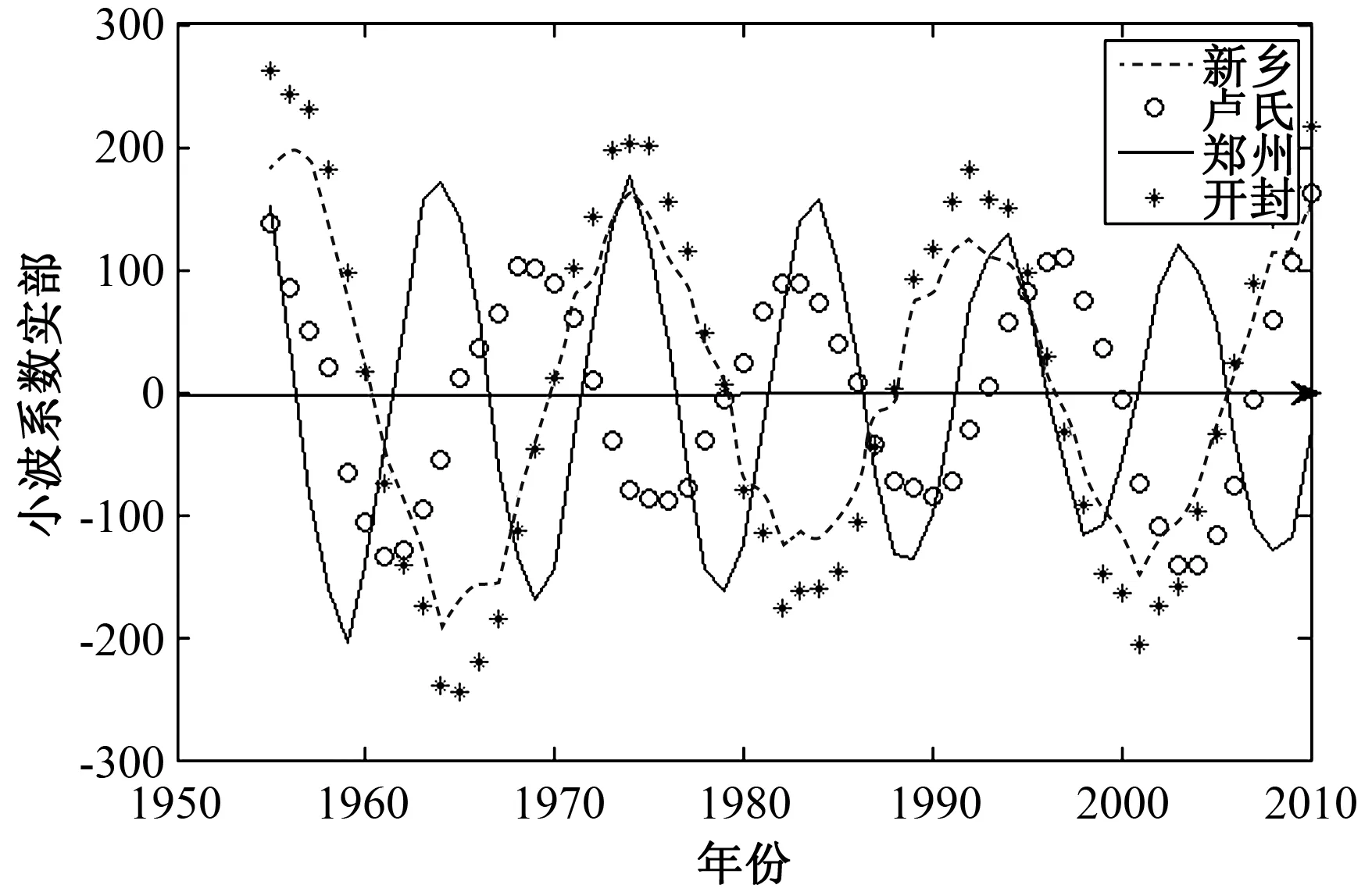
图5 第一主周期趋势图Fig.5 First main cycle trend graph
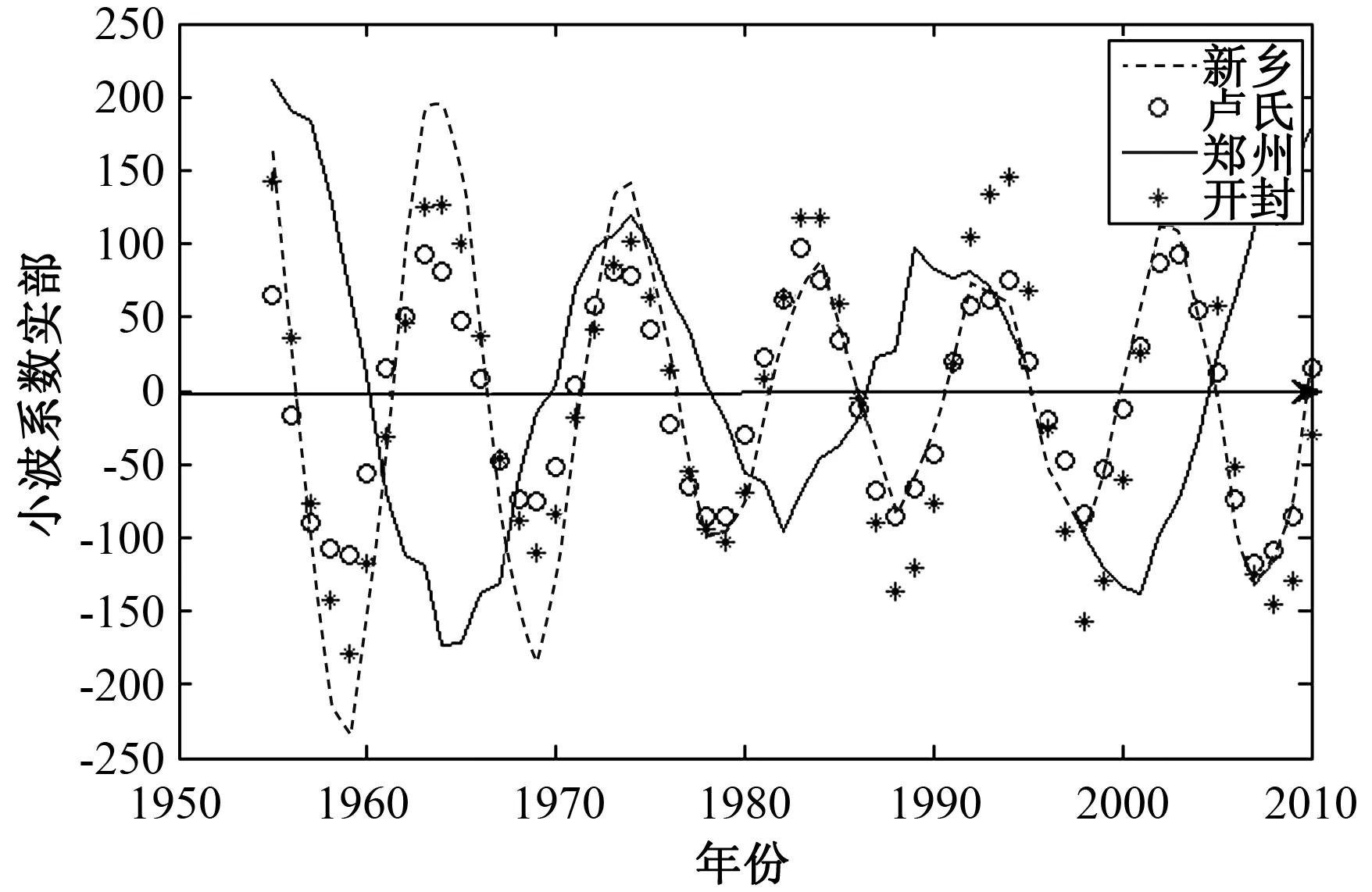
图6 第二主周期趋势图Fig.6 Second main cycle trend graph
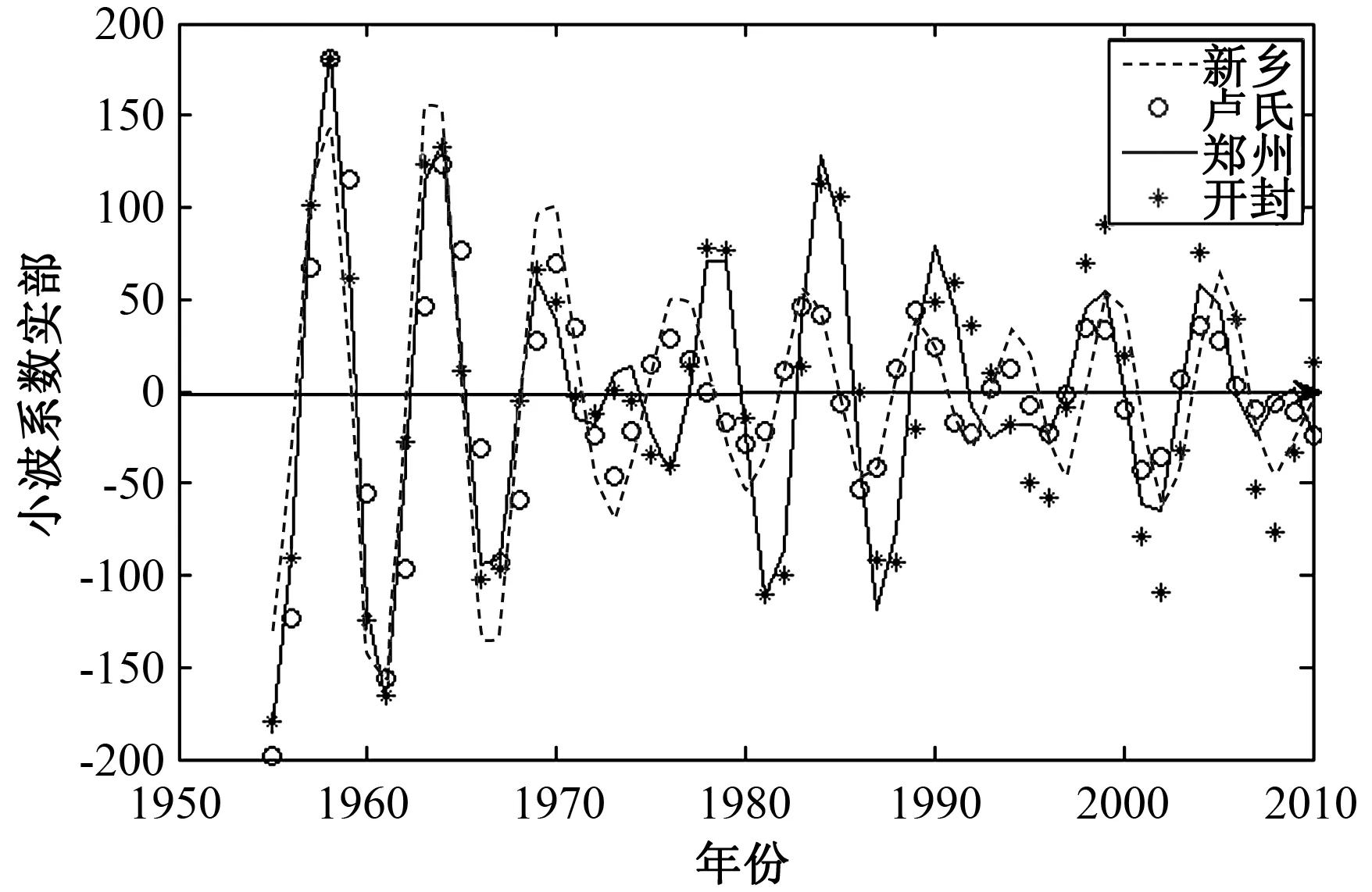
图7 第三主周期趋势图Fig.7 Third main cycle trend graph
综合图5~7的主周期趋势图得出:上述四地区降水第一主周期趋势基本保持一致,平均周期为18 a左右,随着时间尺度的变化以及地理位置、季节等因素的影响,区域地理差异随着小周期的波动而逐渐凸显出来.
3 Z指数分析
由于某一时段的降水量一般不服从正态分布, 现假设降水量服从Person-Ⅲ型分布[8],对降水序列进行正态化处理,计算公式为
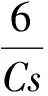
(1)
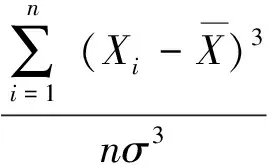
(2)
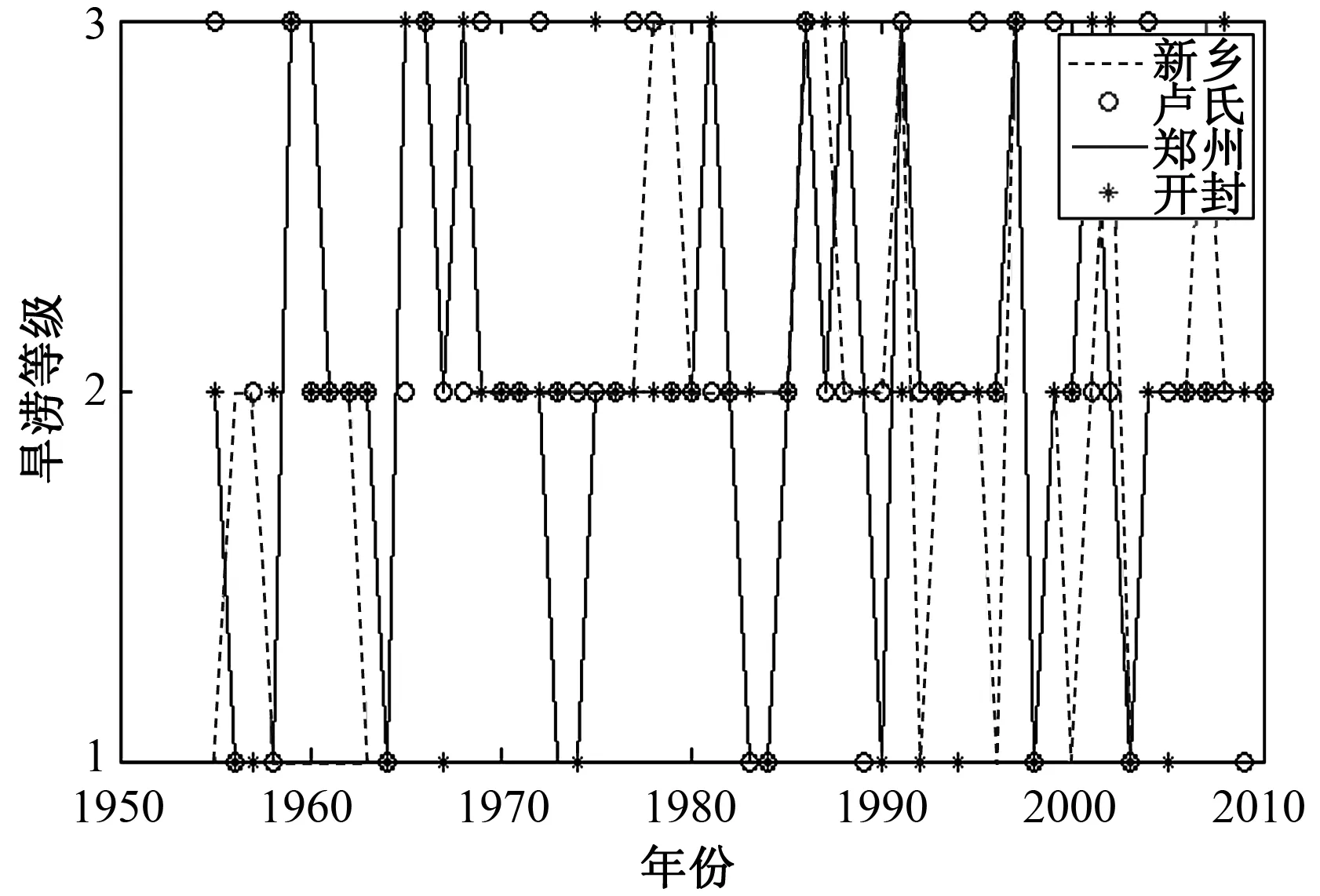
图8 河南四地区1955—2010年旱涝等级图Fig.8 Three levels of drought and flood from 1955 to 2010 in four areas of Henan Province注:1-涝,2-正常,3-旱
(3)
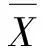
依据文献[7]中的旱涝指标,计算出河南四地区56年的指数值并统计出对应的旱涝等级,结果如图8.从图8可以看出,河南四地区1959—1960年、1966—1968年、1985—1990年、1997年为旱,1956—1958年、1963—1964年、1983—1984年、1998年、2003年为涝,其余旱涝等级显示为正常.通过对比得出,河南四地区的旱涝等级虽然不尽相同,但旱涝走势基本保持一致,这对河南省整体的旱涝规律有一定的研究意义.
由表2可知,56年中这四地区出现旱年次数最多的是新乡,占总体的25.00%;出现涝年次数最多的是开封,占21.43%;总体来说,新乡、卢氏、郑州、开封四地的降水情况大体上还是维持在正常年水平.

表2 旱涝对应发生频率/%Tab.2 Correspondence frequency of drought and flood/%
4 结论
1)河南四地区的区域降水量基本在200~800 mm之间波动,其中新乡降水变化倾向率为-13.809 mm/(10 a),呈弱下降趋势,而卢氏、郑州、开封的降水变化趋势基本不明显.总体上,河南区域降水量由北向南、从西到东逐渐增多.
2)河南四地区的年降水量具有一定的多时间尺度结构及多主周期变化规律.由Morlet小波分析,可知河南四地区降水第一主周期趋势基本保持一致,随着时间尺度的变化,区域地理差异随着小周期的波动而逐渐凸显出来,存在不同降水周期进而调节整个时间域内的变化特征,平均周期为18 a左右.
3)由相关系数结合地理位置判断郑州、新乡、开封降水相关程度明显高于卢氏,据此反映出地理位置与降水之间存在一定的相关性.
4)局部地区的旱涝年交替出现,1959—1960年、1966—1968年、1985—1990年、1997年为旱,1956—1958年、1963—1964年、1983—1984年、1998年、2003年为涝,其余年份的旱涝等级显示为正常.
[1] 张丽,胡娟萍,李宝玉.郑州市1951—2011年降水及气温的变化特征分析[J].华北水利水电大学学报(自然科学版), 2014, 35(3):19-23.
[2] 王跃民,鲁慧霞,刘璟瑜,等. 3个不同旱涝指标划分旱涝等级的比较研究[J].现代农业科技, 2011(7):326-327.
[3] 郝秀平,张振伟,马建琴,等.基于标准降水指数的河南省干旱时空演变规律分析[J].水电能源科学, 2013,31(9):4-7.
[4] 国家气象信息中心.国家气象科学数据共享服务平台[DB/OL]. [2017-10-25].http://data.cma.cn/site/index.html.
[5] 邵晓梅,许月卿,严昌荣.黄河流域降水序列变化的小波分析[J].北京大学学报(自然科学版), 2006, 42(4):503-509.
[6] 潘雅婧,王仰麟,彭建,等.基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J]. 地理研究, 2012, 31(5):811-820.
[7] 孙燕,朱明月. 1961—2011年江苏夏季分级雨日的气候特征[J]. 气象科学,2014,34(2):200-205.
[8] 鞠笑生,杨贤为,陈丽娟,等.我国单站旱涝指标确定和区域旱涝级别划分的研究[J].应用气象学报,1997,8(1):27-34.
StudyonPrecipitationCycleandSpatialDistributionofFourAreasinHenanProvinceof56Years
PENG Gaohui1, LI Fei1, YANG Qian1, WANG Jinpeng2
(1.SchoolofMathematicsandStatistics,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450046,China;2.FirstEngineeringBureallofHenanWaterConservancy,Zhengzhou450000,China)
Based on the annual precipitation data of four areas in Henan Province such as Xinxiang, Lushi, Zhengzhou and Kaifeng, during 1955—2010, using linear inclination estimation, wavelet analysis,Zindex and other methods, the characteristics of precipitation in four regions of Henan: trend, correlation, periodicity, drought and flood conditions were studied. The results showed that the spatial precipitation in the four regions of Henan Province is gradually increased from west to east, and gradually increased from south to north. The overall trend of the first main period remained the same, the average cycle is about 18 years, along with change of time scale, regional geographic differences is with small periodic fluctuations gradually highlighted.
periodicity; wavelet analysis; linear tendency analysis; drought-flood analysis;Zindex
2017-10-08
河南省高校科技创新人才支持计划资助(15HASTIT046);河南省科技攻关项目资助(152102110095);河南省高等学校重点科研项目资助(15A570008);华北水利水电大学大学生创新创业训练计划项目(2016XB135)
彭高辉(1978—),男,河南新乡人,华北水利水电大学数学与统计学院副教授,主要研究方向:数据分析与算法实现、水文分析等.
10.3969/j.issn.1007-0834.2017.04.004
TV213.4
A
1007-0834(2017)04-0017-05

