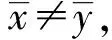关于强T-拟凸函数的几点注记
胡 芳
(武汉生物工程学院 计算机与信息工程系,湖北 武汉 430415)
关于强T-拟凸函数的几点注记
胡 芳
(武汉生物工程学院 计算机与信息工程系,湖北 武汉 430415)
主要讨论了强T-拟凸函数的判定方法,得到某些新的结论,推广了文献中的主要结论.
拟凸函数;T-拟凸函数;强T-拟凸函数
0 引言
T-拟凸函数是一类非常重要的广义凸函数,已有大量的文献对此进行了研究.2007年,宁刚在文献[1]中讨论了T-凸函数与T-拟凸函数的等价条件;2009年,钟超瑾给出了T-凸集上的函数的半连续性与T-拟凸性之间的关系[2];2011年,韦丽兰等人在文献[3]中讨论了在上(下)半连续的假设条件下,T-凸函数与T-拟凸函数的等价条件。随着凸性研究的深入,T-拟凸函数,强T-拟凸函数及严格T-拟凸函数越来越成为更加重要的广义凸函数,然而,对于强T-拟凸函数的研究非常有限.本文主要讨论强T-拟凸函数的判定方法,得到了某些新的结论,推广了文献中的主要结论.
1 定义
定义1[1]设D⊂Rn,f是定义在D上的n元实值函数,若存在映射T:Rn→Rn使得D为T-凸集,且对∀x,y∈D,及任意实数λ∈[0,1],恒有
f[λT(x)+(1-λ)T(y)]≤max{f(T(x)),f(T(y))},
(1)
则称f是D上的T-拟凸函数.如果-f是D上的T-拟凸函数,则称f是D上的T-拟凹函数.
定义2[4]设D⊂Rn,f是定义在D上的n元实值函数,映射T:Rn→Rn使得D为T-凸集且T(D)为凸集,若对∀x,y∈D,x≠y,以及任意实数λ∈[0,1],有
f[λT(x)+(1-λ)T(y)] (2) 则称f是D上的强T-拟凸函数. 定义3[4]设D⊂Rn,f是定义在D上的n元实值函数,映射T:Rn→Rn使得D为T-凸集且T(D)为凸集,对∀x,y∈D,f(T(x))≠f(T(y)),以及任意实数λ∈[0,1],有 f[λT(x)+(1-λ)T(y)] (3) 则称f是D上的严格T-拟凸函数. 引理[2]设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的n元实值下半连续函数,且存在λ∈(0,1)使得 f[λT(x)+(1-λ)T(y)]≤max{f(T(x)),f(T(y)),∀x,y∈D}, (4) 则f是D上的T-拟凸函数. 定理1设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的n元实值下半连续函数,则f是D上的强T-拟凸函数的充要条件是对于∀x,y∈D,x≠y,存在λ∈(0,1),λ依赖x,y,使得 f[λT(x)+(1-λ)T(y)] (5) 证明1)(充分条件)显然成立. 2)(必要条件)反证法.假设f不是强T-拟凸函数,则∃x1,x2∈D,x1≠x2及 ∂0∈(0,1),有 f[∂0T(x1)+(1-∂0)T(x2)]≥max{f(T(x1)),f(T(x2))}, (6) 由假设及条件,可根据引理知f是D上的T-拟凸函数,即有 f[∂0T(x1)+(1-∂0)T(x2)]≤max{f(T(x1)),f(T(x2))}, (7) 由(6)、(7)可知 f[∂0T(x1)+(1-∂0)T(x2)]=max{f(T(x1)),f(T(x2))}, (8) 不妨设f(T(x1))≥f(T(x2)),令T(z)=∂0T(x1)+(1-∂0)T(x2). a)若f(T(x2))>f(T(x1)),则(8)可简化为 f(T(z))=max{f(T(x1)),f(T(x2))}=f(T(x2))>f(T(x1)), (9) 对z,x2,由条件可得,存在λ0∈(0,1),有 f[λ0T(z)+(1-λ0)T(x2)] (10) 记(T(z),T(x2))={λT(z)+(1-λ)T(x2)|λ∈(0,1)},又由D是T-凸集且T(D)是凸集,则存在z1,使得T(z1)=λ0T(z)+(1-λ0)T(x2),显然,T(z1)∈(T(z),T(x2)),则(10)可简化为 f(T(z1)) (11) 显然,T(z)∈(T(x1),T(z1)).又,f是D上的T-拟凸函数,对x1,z1,∀λ∈(0,1),有 f(T(z))=f(λT(x1)+(1-λ)T(z1))≤max{f(T(x1)),f(T(z1))}, (12) 由(9)、(11)、(12)可知矛盾,故假设不成立. b)若f(T(x2))=f(T(x1)),(8)式化简为 f(T(z))=max{f(T(x1)),f(T(x2))}=f(T(x1))=f(T(x2)), (13) 对x1,z用条件知,∃λ1∈(0,1)有 f(λ1T(x1)+(1-λ1)T(z)) (14) 对x2,z用条件知,∃λ2∈(0,1)有 f(λ2T(x2)+(1-λ2)T(z)) (15) 令T(y1)=λ1T(x1)+(1-λ1)T(z),T(y2)=λ2T(x2)+(1-λ2)T(z),则T(z)∈(T(y1),T(y2)). 结合(13)式,化简(14), (15)分别为 f(T(y1)) (16) f(T(y2)) (17) 又,f是D上的T-拟凸函数,对y1,y2,∀λ∈(0,1),有 f(T(z))≤max{f(T(y1)),f(T(y2))}, (18) 显然(16), (17), (18)式矛盾. 综上所述,假设不成立,即定理的必要条件成立. 推论1设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的n元实值下半连续函数, 若存在λ∈(0,1),对于∀x,y∈D,x≠y,有 f[λT(x)+(1-λ)T(y)] (19) 则f是D上的强T-拟凸函数. 推论2设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的T-拟凸函数, 若对∀x,y∈D,x≠y,当f(T(x))=f(T(y))时,∃λ∈(0,1),有 f[λT(x)+(1-λ)T(y)] (20) 则f是D上的强T-拟凸函数. 定理2设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的严格T-拟凸函数, 且对∀x,y∈D,x≠y,当f(T(x))=f(T(y))时, ∃λ∈(0,1),有 f[λT(x)+(1-λ)T(y)] (21) 则f是D上的强T-拟凸函数. 证明反证法. 设f不是D上的强T-拟凸函数,则∃x1,x2∈D,x1≠x2,λ1∈(0,1),使得 f[λ1T(x1)+(1-λ1)T(x2)]≥max{f(T(x1)),f(T(x2))}, (22) D是T-凸集且T(D)是凸集,则∃z0∈D,使得T(z0)=λ1T(x1)+(1-λ1)T(x2),则有 f(T(z0))≥max{f(T(x1)),f(T(x2))}. (23) 1)若f(T(x1))>f(T(x2)),由f是定义在D上的严格T-拟凸函数,对于x1,x2∈D,λ1∈(0,1),有 f[λ1T(x1)+(1-λ1)T(x2)] (24) 即f(T(z0)) 2)若f(T(x1))=f(T(x2)),由条件可知,∃λ0∈(0,1),使得 f[λ0T(x1)+(1-λ0)T(x2)] (25) D是T-凸集且T(D)是凸集,则∃z1∈D,使得T(z1)=λ0T(x1)+(1-λ0)T(x2). (25)式化简为 f(T(z1)) (26) T(z1)≠T(z2),则T(z1)∈(T(x1),T(z0))或T(z1)∈(T(z0),T(x2)). 若T(z1)∈(T(x1),T(z0)),则T(z0)∈(T(z1),T(x2)). 由f(T(z1))≠f(T(x2)),又f是严格T-拟凸函数,对于z1,x2∈D,有 f(T(z0)) (27) 与(23)式矛盾. 若T(z1)∈(T(z0),T(x2)),则T(z0)∈(T(x1),T(z1)). 由f(T(x1))≠f(T(z1)),又f是严格T-拟凸函数,对于z1,x1∈D,有 f(T(z0)) (28) 与(23)式矛盾. 综上所述,假设不成立. 定理3设D⊂Rn,若存在映射T:Rn→Rn使得D是T-凸集且T(D)是凸集,f是定义在D上的T-拟凸函数, ∃∂0∈(0,1)对∀x,y∈D,当x≠y时,有 f[∂0T(x)+(1-∂0)T(y)] (29) 则f是D上的强T-拟凸函数. 证明假设f不是D上的强T-拟凸函数.∃x,y∈D,λ0∈(0,1),虽有x≠y,但 f[λ0T(x)+(1-λ0)T(y)]≥max{f(T(x)),f(T(y))}. (30) 令T(z)=λ0T(x)+(1-λ0)T(y),(30)式简化为 f(T(z))≥max{f(T(x)),f(T(y))}. (31) 由f是定义在D上的T-拟凸函数,则∀x,y∈D,均有 f(T(z))≤max{f(T(x)),f(T(y))}, (32) 由(31),(32)可知 f(T(z))=max{f(T(x)),f(T(y))}. (33) (34) (35) (36) 由(34), (35), (36)可知 f(T(z)) (37) 显然(37)和(33)矛盾,则假设不成立. [1] 宁刚.E-凸函数的若干性质[J]. 运筹学学报,2007,11(1):121-126. [2] 钟超瑾.E-凸集上的函数的半连续性与E-拟凸性[J]. 广东教育学院学报,2009,29(3):48-51. [3] 韦丽兰,黄雪燕.E-凸函数和E-拟凸函数的等价条件[J].数学的实践与认识,2011,41(15):191-197. [4] 邢志栋,王双虎. 拟凸函数的一个充分条件[J]. 纯粹数学与应用数学,1990,2(6):76-79. SomeNotesonStrongT-QuasiConvexFunction HU Fang (DepartmentofComputerandInformationEngineering,WuhanInstituteofBioengineering,Wuhan430415,China) Mainly discusses the determination method of strongT-quasi convex function, and obtains some new conclusions, and generalizes the main conclusions in the literatures. quasi-convex function;T-quasi-convex function; strongT-quasi convex function 2017-08-03 胡 芳(1984—),女,湖北武汉人,武汉生物工程学院计算机与信息工程系副教授,主要研究方向:高等数学教学、凸分析. 10.3969/j.issn.1007-0834.2017.04.005 O13 A 1007-0834(2017)04-0022-032 主要结论