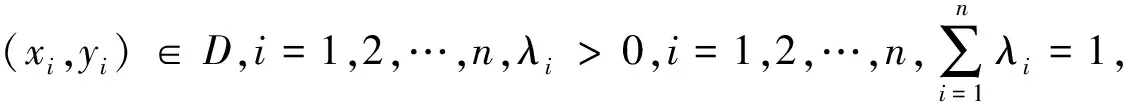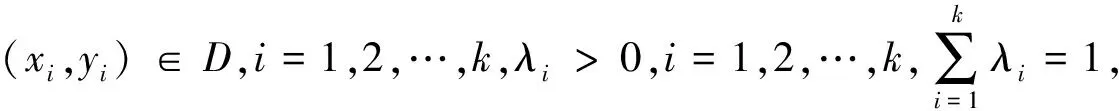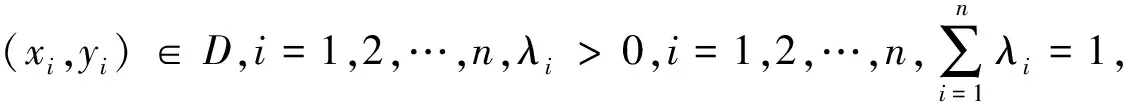多元凸函数及其Jensen不等式
成凯歌
(浙江旅游职业学院 基础部,浙江 杭州 311231)
多元凸函数及其Jensen不等式
成凯歌
(浙江旅游职业学院 基础部,浙江 杭州 311231)
凸函数是一类性质特殊的函数,一些重要性质有着广泛的应用,凸集和凸函数在泛函分析、最优化理论、数理经济学等领域占据着重要地位. 借助一维凸集和凸函数概念,介绍了多元凸函数的概念、判断、复合运算和多元凸函数的Jensen不等式.
凸集;凸函数;复合运算;Jensen不等式
函数的凹凸性反映函数图像的弯曲方向,掌握函数的凹凸性是准确把握函数性态、描绘函数图像的重要手段,另外,凸函数作为一类重要的函数,其具有的重要性质,在函数极值、不等式研究、数学规划、逼近论、对策论等领域有着广泛的应用.目前对于一元凸函数的性质及其应用已经有了广泛的研究,取得了丰富的成果[1-10]. 但对于涉及多元凸函数的讨论,已经取得的结果并不多,本文在给出多元凸函数概念的基础上,对多元凸函数的判断,多元凸函数的复合运算及其Jensen不等式进行了研究,并获得了一些成果.
1 预备知识
定义1[11]某集合称为凸集, 是指连接该集合中的任何两点的连接直线段上的点都在该集合中.
定义2[11]设X是一个线性空间,x1,x2∈X为任意两点,称
[x1,x2]={x|x=λx1+(1-λ)x2,λ∈[0,1]}
为连接点x1,x2的闭线段.
定义3[11]设X是一个线性空间, 子集A⊂X称为凸集,是指对x1,x2∈A及λ∈[0,1],有
λx1+(1-λ)x2∈A
或者
[x1,x2]∈A.
定义4[12]设f(x)在区间I上有定义, 如果对于任意x1,x2∈I和λ∈(0,1),有
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),
(1)
则称f(x)为区间I上的凸函数,如果(1)中不等号改为严格不等号,则称f(x)为区间I上的严格凸函数.
定义5[12]设f(x)在区间I上有定义, 如果对于任意x1,x2∈I和λ∈(0,1),有
f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),
(2)
则称f(x)为区间I上的凹函数,如果(2)中不等号改为严格不等号,则称f(x)为区间I上的严格凹函数.
定义6[13]设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,如果对∀λ∈(0,1),以及∀(x1,y1),(x2,y2)∈D,有
f(λx1+(1-λ)x2,λy1+(1-λ)y2)≤λf(x1,y1)+(1-λ)f(x2,y2),
(3)
则称f(x,y)为区域D上的凸函数,如果(3)中不等号改为严格不等号,则称f(x,y)为区域D上的严格凸函数.
定义7[13]设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,如果对∀λ∈(0,1),以及∀(x1,y1),(x2,y2)∈D,有
f(λx1+(1-λ)x2,λy1+(1-λ)y2)≥λf(x1,y1)+(1-λ)f(x2,y2),
(4)
则称f(x,y)为区域D上的凹函数,如果(4)中不等号改为严格不等号,则称f(x,y)为区域D上的严格凹函数.
定义8设D⊂R2是平面上的一个点集,函数f(x,y)在D上有定义,对∀(x1,y1),(x2,y2)∈D,如果当x1 f(x1,y1)≤f(x2,y2), (5) 则称f(x,y)为区域D上的增函数,如果(5)中不等号改为严格不等号,则称f(x,y)为区域D上的严格增函数. 定义9设D⊂R2是平面上的一个点集,函数f(x,y)在D上有定义,对∀(x1,y1),(x2,y2)∈D,如果当x1 f(x1,y1)≥f(x2,y2), (6) 则称f(x,y)为区域D上的减函数,如果(6)中不等号改为严格不等号,则称f(x,y)为区域D上的严格减函数. 对于许多函数而言,从定义出发判定它是否为凸函数往往是非常困难的,所以,寻求凸函数更为简洁的判定方法,是最为感兴趣的问题.此外,函数的复合运算是函数运算的重要内容之一,也是构造新函数的重要手段之一,在复合运算过程中,令人非常感兴趣的是原来函数的性质在通过复合运算得到的新函数里能否继续保持下来, 以下先讨论这两个方面的问题. 2.1 多元凸函数的判断 定理1设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,且fx(x,y)和fy(x,y)在D上的每一点都存在. 假如对D中任意两点(x1,y1),(x2,y2),有 f(x2,y2)≥f(x1,y1)+fx(x1,y1)(x2-x1)+fy(x1,y1)(y2-y1), (7) 则f(x,y)为区域D上的凸函数. 证明设(x1,y1),(x2,y2)为D上的任意两点,对任意λ∈(0,1),令 x3=λx1+(1-λ)x2,y3=λy1+(1-λ)y2, 则有 x1-x3=(1-λ)(x1-x2),y1-y3=(1-λ)(y1-y2), x2-x3=λ(x2-x1),y2-y3=λ(y2-y1). 根据(7)式,有 f(x1,y1)≥f(x3,y3)+(1-λ)fx(x3,y3)(x1-x2)+(1-λ)fy(x3,y3)(y1-y2), f(x2,y2)≥f(x3,y3)+λfx(x3,y3)(x2-x1)+λfy(x3,y3)(y2-y1). 分别用λ和1-λ乘以上述两式并相加,得 λf(x1,y1)+(1-λ)f(x2,y2)≥f(x3,y3)=f(λx1+(1-λ)x2,λy1+(1-λ)y2). 所以,f(x,y)为区域D上的凸函数. 注定理1表明,如果曲面z=f(x,y)总是在它每一点切平面的上方,则f(x,y)为区域D上的凸函数. 定理2设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,且f(x,y)在D上存在所有的二阶连续偏导数. 如果对D中任意一点(x,y),有 fxx(x,y)≥0,fxy(x,y)≥0,fyy(x,y)≥0, (8) 则f(x,y)为区域D上的凸函数. 证明设(x1,y1),(x2,y2)为D上的任意两点,由多元函数的Taylor公式,存在θ∈(0,1),使得 (9) 根据条件(8),有 (10) 由(9)和(10)式,即得(7)式成立,从而,由定理1得f(x,y)为区域D上的凸函数. 2.2 一元凸函数和二元凸函数的复合运算 设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,则有以下定理3. 定理3假设f(x,y)为区域D上的凸函数,g(x)为区间J⊃f(D)上的凸增函数,则g∘f(x,y)为区域D上的凸函数. 证明对∀λ∈(0,1),以及∀(x1,y1),(x2,y2)∈D,有 f(λx1+(1-λ)x2,λy1+(1-λ)y2)≤λf(x1,y1)+(1-λ)f(x2,y2), 结合g(x)的递增性及凸性,得 g∘f(λx1+(1-λ)x2,λy1+(1-λ)y2)=g(f(λx1+(1-λ)x2,λy1+(1-λ)y2))≤ g(λf(x1,y1)+(1-λ)f(x2,y2))=λg(f(x1,y1))+(1-λ)g(f(x2,y2))= λg∘f(x1,y1)+(1-λ)g∘f(x2,y2), 所以,g∘f(x,y)为区间D上的凸函数. 类似上述的讨论,即可得以下结论. 定理4假设f(x,y)为区域D上的凸函数,g(x)为区间J⊃f(D)上的凹减函数,则g∘f(x,y)为区域D上的凹函数. 定理5假设f(x,y)为区域D上的凹函数,g(x)为区间J⊃f(D)上的凹增函数,则g∘f(x,y)为区域D上的凹函数. 定理6假设f(x,y)为区域D上的凹函数,g(x)为区间J⊃f(D)上的凸减函数,则g∘f(x,y)为区域D上的凸函数. 设D⊂R2是平面上的一个凸集,函数f(x,y)定义在区域D⊂J×J上,g(x)定义在区间J上,对∀(x,y)∈D,有(g(x),g(y))∈D,则有以下定理. 定理7假设g(x)为区间J上的凸函数,f(x,y)为区域D上的凸增函数,则F(x,y)=f(g(x),g(y))为区域D上的凸函数. 证明对∀λ∈(0,1),以及∀(x1,y1),(x2,y2)∈D,由g(x)的凸性,得 g(λx1+(1-λ)x2)≤λg(x1)+(1-λ)g(x2), g(λy1+(1-λ)y2)≤λg(y1)+(1-λ)g(y2), 结合f(x,y)的递增性以及凸性,得 F(λx1+(1-λ)x2,λy1+(1-λ)y2)=f(g(λx1+(1-λ)x2),g(λy1+(1-λ)y2))≤ f(λg(x1)+(1-λ)g(x2),λg(y1)+(1-λ)g(y2))≤ λf(g(x1),g(y1))+(1-λ)f(g(x2),g(y2))=λF(x1,y1)+(1-λ)F(x2,y2), 所以,g∘f(x,y)为区域D上的凸函数. 类似上述的讨论,即可得以下结论. 定理8假设g(x)为区间J上的凸函数,f(x,y)为区域D上的凹减函数,则F(x,y)=f(g(x),g(y))为区域D上的凹函数. 定理9假设g(x)为区间J上的凹函数,f(x,y)为区域D上的凹增函数,则F(x,y)=f(g(x),g(y))为区域D上的凹函数. 定理10假设g(x)为区间J上的凹函数,f(x,y)为区域D上的凸减函数,则F(x,y)=f(g(x),g(y))为区域D上的凸函数. 2.3 二元凸函数和二元凸函数的复合运算 设D1,D2⊂R2都是平面上的凸集,函数g(x,y)在D2上有定义,f1(x,y)和f2(x,y)都在D1上有定义,且满足{(f1(x,y),f2(x,y))|(x,y)∈D1}⊂D2. 定理11假设f1(x,y)和f2(x,y)都是D1上的凸函数,g(x,y)为区域D2上的凸增函数,则F(x,y)=g(f1(x,y),f2(x,y))为区域D1上的凸函数. 证明对∀λ∈(0,1),以及∀(x1,y1),(x2,y2)∈D1,由f1(x,y),f2(x,y)的凸性,得 f1(λx1+(1-λ)x2,λy1+(1-λ)y2)≤λf1(x1,y1)+(1-λ)f1(x2,y2), f2(λx1+(1-λ)x2,λy1+(1-λ)y2)≤λf2(x1,y1)+(1-λ)f2(x2,y2), 结合g(x,y)的递增性和凸性,得 F(λx1+(1-λ)x2,λy1+(1-λ)y2)= g(f1(λx1+(1-λ)x2,λy1+(1-λ)y2),f2(λx1+(1-λ)x2,λy1+(1-λ)y2))≤ g(λf1(x1,y1)+(1-λ)f1(x2,y2),λf2(x1,y1)+(1-λ)f2(x2,y2))≤ λg(f1(x1,y1),f2(x1,y1))+(1-λ)g(f1(x2,y2),f2(x2,y2))= λF(x1,y1)+(1-λ)F(x2,y2), 所以,F(x,y)=g(f1(x,y),f2(x,y))为区域D1上的凸函数. 类似上述的讨论,即可得以下结论. 定理12假设f1(x,y)和f2(x,y)都是D1上的凸函数,g(x,y)为区域D2上的凹减函数,则F(x,y)=g(f1(x,y),f2(x,y))为区域D1上的凹函数. 定理13假设f1(x,y)和f2(x,y)都是D1上的凹函数,g(x,y)为区域D2上的凹增函数,则F(x,y)=g(f1(x,y),f2(x,y))为区域D1上的凹函数. 定理14假设f1(x,y)和f2(x,y)都是D1上的凹函数,g(x,y)为区域D2上的凸减函数,则F(x,y)=g(f1(x,y),f2(x,y))为区域D1上的凸函数. 由以上讨论可得:在凸函数的复合过程中,在内函数是凸函数的条件下,当外函数是凸增函数时,复合函数是凸函数,而当外函数是凹减函数时,复合函数是凹函数;在内函数是凹函数的条件下,当外函数是凸减函数时,复合函数是凸函数,而当外函数是凹增函数时,复合函数是凹函数. 2.4 Jensen不等式 设D⊂R2是平面上的一个凸集,函数f(x,y)在D上有定义,则有 (11) 设(xi,yi)∈D,i=1,2,…,k,k+1,及 这就证明了对任意给定正整数n≥2,凸函数f(x,y)总有不等式(11)成立. 上述讨论的定理15表明,对于多元凸函数Jensen不等式依然成立. 由定义7及定理15的证明即可得定理16. (12) [1] 何敏藩,胡诗国.凹凸函数的两个定义的等价性证明及应用[J].广东第二师范学院学报,2017,37(3):50-53. [2] 韩艳娜.关于函数凹凸性的教学探讨[J].佳木斯职业学院学报,2016,162(5):282-283. [3] 张亚楠,刘长剑.关于凸函数单侧导数的连续性[J].大学数学,2015,31(4):53-54. [4] 时统业,谢井,李鼎.关于凸函数的新不等式[J].高等数学研究,2016,19(1):51-53. [5] 吴善和.平方凸函数与琴生型不等式[J].首都师范大学学报(自然科学版),2005,26(1):16-21. [6] 赵宇,黄金莹,王希圆.数学分析中的条件极值问题[J].大学数学,2013,29(2):102-106. [7] 赵秀.谈谈凸函数及其应用[J].数学教学与研究,2017(7):56-57. [8] 张鑑,顾春,石焕南.凸函数的两个性质的控制证明[J].高等数学研究,2016,19(4):32-33. [9] 曹泽龙.凸函数与不等式[J].中学数学月刊,2017(6):64-66. [10] 李德奎.一元函数凹凸性的一个充分条件[J].辽宁大学学报(自然科学版),2017,44(2):114-117. [11] 尚亚东,游淑军.凸函数及其在不等式证明中的应用[J].广州大学学报(自然科学版),2005,4(1):1-6. [12] 华东师范大学数学系.数学分析:上册[M].4版.北京:高等教育出版社,2010:151-156. [13] 廖俊俊,吴洁.关于凸性的一些探讨[J].大学数学,2016,32(6):91-95. MultivariateConvexFunctionandJensenInequalities CHENG Kaige (DepartmentofBasic,TourismCollegeofZhejiang,Hangzhou311231,China) The convex function is a function with the special properties, and some of its important properties are used widely. Convex sets and convex functions play the important roles in functional analysis, optimization theory, mathematical economics, etc. With the help of the concepts of convex sets and convex functions in one-dimension, introduces the concept of multivariate convex function, judgment, composite operation, and Jensen inequality operation of the multivariate convex function. convex set; convex function; compound operation; Jensen inequality 2017-09-24 浙江旅游职业学院优质课程资助项目(2017ZLY012) 成凯歌(1968—),男,浙江杭州人,浙江旅游职业学院基础部讲师. 10.3969/j.issn.1007-0834.2017.04.002 O174.6 A 1007-0834(2017)04-0006-052 主要结果