把握问题关联,衔接拓展促解
杨振


[摘 要] 衔接生长性几何题是近几年中考的常见题型,问题设置具有层次性、递进性和衔接性. 由于问题的条件、结论存在紧密的关联,所以求解时需要充分利用问题的关联性进行思维的递进思考. 本文结合中考题对生长性几何问题进行深度剖析,并开展解后反思,提出相应的教学建议,与读者交流、探讨.
[关键词] 几何;正方形;生长;衔接
真题解析,解法点评
考题1 (2017年安徽中考)已知一正方形ABCD,边AB的中点为M.
(1)如图1,点G为线段CM上一点,且∠AGB=90°,连接AG,BG,并延长,分别交边BC,CD于点E和点F.
①试证明:BE=CF;
②试证明:BE2=BC·CE.
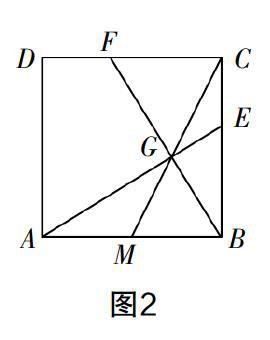
(2)如图2,在边BC上取一点E,使其满足条件BE2=BC·CE,连接AE,交CM于点G,再连接BG并延长后交CD于点F,试求tan∠CBF的值.
分析 (1)①要证BE=CF,可以将其放在Rt△ABE和Rt△BCF中,通过证明三角形全等来获得. ②由于涉及边之间的乘积关系,所以可尝试通过三角形相似以及等角代换来证明,即先证明△CEG与△CGB相似,根据相似性质得CG2=CE·CB,然后结合CG=BE完成证明.
点评 本题为涉及正方形的几何综合题,主要考查正方形的性质,全等三角形,相似三角形的判定与性质,以及黄金分割点等知识. 本题有两个小问,两者之间有着紧密的联系. 第(2)问是对第(1)问的拓展生长,即后一问的条件是在前一问结论上的变式拓展,问题设计具有鲜明的层次性和递进性. 在问题的求解过程中,均是基于不同的条件进行问题转化,将待求结论放在基础图形中利用三角形全等或相似的性质来求解,尤其是第(2)问,巧妙地将第(1)问线段的等量关系转化为数学上的黄金分割点,利用其线段的比例关系实现三角形正切的求值. 对于中考具有拔高生长性的问题,在求解后一问时需要充分利用前一问结论和解题思路的启示作用,基于问题情境进行转化,实现问题条件的衔接性思考,对待求结论进行拓展性分析.
考题衔接,题型再析
近几年中考几何综合题特别注重设问的层次性和递进性,初始问题起点较低,平淡中蕴含几何规律,之后的问题是对前者的衔接与拓展,可利用前一问题的结论逐步引导学生进行思维的深层探索,充分挖掘结论的一般性. 题型的设置呈现“低起点,高产出”的特点,下面笔者对同类型的几何综合题进行深度剖析.
考题2 (2015年四川甘孜、阿坝中考)现有一正方形ABCD,点E,F分别位于正方形的边BC,CD上,且AF与DE相交于点G,当点E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立. 试探究下列问题:
(1)如图4,如果点E不为BC的中点,点F不为CD的中点,且CE=DF,试探究上述结论①②是否依然成立,并说明理由.
(2)如图5,如果点E,F分别在CB,DC的延长线上,且CE=DF,试判断上述结论①②是否依然成立. 如果成立,请写出具体的证明过程;如果不成立,请说明理由.
(3)如图6,在(2)成立的基础上,连接AE和EF,如果点M,N,P,Q分别为AE,EF,FD,AD的中点,试判断四边形MNPQ是“矩形”“菱形”“正方形”中的哪一种,并证明结论.
分析 (1)证明结论①②,可以将其放在三角形中,通过证明三角形全等来获得证明条件,如证明△ADF≌△DCE. 利用全等性质可得AF=DE,∠DAF=∠CDE,通过角度的代换可得∠ADG+∠DAF=90°,从而∠AGD=90°,于是AF⊥DE.
(2)同(1)的证明思路和步骤一样,此处不赘述.
评析 本题的设问采用“移步换景”的变换方式,对结论的探究从特殊到一般逐层递进,最终利用所证结论求证了后者的拓展性问题. 与考题1所不同的是,设问关系存在差异,考题1的设问主要是对条件与结论的转化,而考题2的设问则是对一般规律的逐步探索,以“求证—应用”的模式完成题型设置,总体来说均是对衔接、生长性问题设计的充分体现.
解后之思,教学之思
1. 学习衔接问题,提升解题思维
上述所解析的两道几何综合题均是衔接生长性的典型题,具有低起点、高产出的鲜明特点,问题的设置层层递进、环环相扣,逐步引导学生进行深层次的思维活动. 每一问的条件、结论、解题策略均不是独立存在的,对于后面的问题探索均有重要的启示作用. 该类题型的设计是对复杂问题的简化变形,其不仅可以充分调动学生的知识经验,还对学生的思维有一定的引导作用. 在实际教学中,教师可以合理地编排练习题,引导学生对问题的结论和条件进行变式、拓展,以提升学生思维的开放性、连续性和递进性,从而形成独立的解题思维.
2. 掌握基础知识,系统归纳整理
几何综合题一般来说涉及的知识点多、图形复杂、问题抽象,求解过程需要不断地对问题进行转化、变形,逐步建立起条件与结论之间的联系. 但无论问题的复杂程度如何,最终都需要利用几何基本性质和定理来求解. 以上述考题为例,解题过程涉及正方形的性质、全等三角形和相似三角形的性质及判定、三角形中線、三角函数等知识,因此基础知识的掌握程度直接影响着学生的解题效率. 教学中,我们要立足教材基础内容,引导学生掌握最基本的知识、技能、思想,并对基础知识进行系统整理,提升知识运用的灵活度.
3. 解读概念定义,提炼基本图形
图形几何作为初中数学的重要内容,中考基于该内容主要考查学生的思维能力和推理能力,尤其体现在具有衔接生长性的问题之中. 对该类问题的求解离不开对问题信息条件的整合、转化,以及对复合图形的提炼、分离. 对图形语言的表达、理解,以及对基本图形的提炼,都将影响解题思路的探索过程. 因此,在教学中,教师有必要对教材的概念、定理进行语言符号的相互转化,以帮助学生深度理解其本质内涵,同时需要结合直观的基本图形对公式、定理进行释义、解读,以促进学生对图形特征和性质的理解,从而有效提升学生提炼基本图形的能力.
结束语
具有衔接、生长性的几何综合题在问题设计上具有紧密的关联性,该类题不仅对学生的解题思路具有一定的引导作用,对学生的解题思维也具有拓展作用. 求解时,需要紧密把握问题之间的关联信息,有效利用已有条件、结论和思路进行思维深层拓展. 教学中,需要教师立足教材内容,扎实学生基础;开展概念、定义的语言互化,结合基本图形加深学生对公式、定理的理解,提升学生基本图形的提炼能力;适当地对习题进行变式、拓展,使学生形成独立的解题思维. 总之,初中教学是知识内容与推理思维的双重活动,结合考题进行实践教学可以提升教学的实效性.

