治“练习课”亦如烹小鲜

邓芸芸

摘  要：练习课是小学数学重要课型，而实际教学中普遍效率不高。教师应选用合适的材料和方法，创设数学情境、传递数学思想、注重数形结合，激发学生学习兴趣，激励学生挑战自我，从而提高练习课的实效。

关键词：小学数学;练习课;有效教学

练习课是小学数学教学的主要课型之一，约占总课时数的一半左右。它是一种有目的、有计划、有指导的训练活动，是学生巩固知识、形成技能、培养能力的重要途径。然而，实际教学中却时常听到教师们说“上练习课时学生学习劲头不足， 教学效率不高”;有的则认为练习课教学内容往往平淡无味，学生兴致不高也是正常的。老子云：“治大国如烹小鲜”，笔者认为，治“练习课”亦如烹小鲜。教师上课恰似厨师做菜，除了选取合适的“素材”，还要凭借高超的技艺，将“油盐酱醋”搭配合理，才能将练习课也上得“色香味”俱全，让学生食欲大开、欲罢不能。

一、情境似“油”，润泽童心

生动有趣的情境能牢牢抓住儿童的心，激发学生的学习兴趣，犹如滴滴香油滋润着食材。和新授课一样，练习课的教学也同样要注重情境的创设。

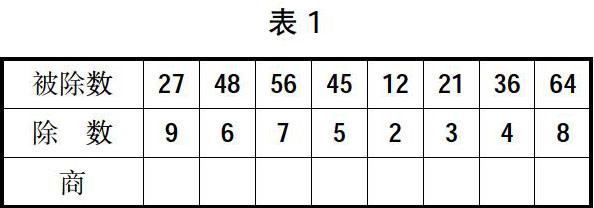
案例1：“捉逃兵”（表1）

在學生顺利地完成教材上的这道题后，笔者创设了一个“捉逃兵”的游戏情境。将已经填好的表格中的一些数字擦去，得到了表2。

师：不好！有些调皮的数字娃娃当“逃兵”了，离开了自己的岗位，请小朋友们来当小警察，赶紧把逃兵捉回来！

生1：我会捉逃兵，第一列的逃兵是9。

师：你是怎么知道的？

生1：我记得刚才第一列的除数就是9，而且根据口诀“三九二十七”，也能知道一定是9。

生2：第二列的逃兵是48，因为只有48除以6才等于8。

生3：还可以用6乘8来算，也是48。

……

在活动中，学生个个兴致高昂，纷纷抢着去抓“逃兵”，并为自己成功捉到了“逃兵”而兴奋不已。而在此过程中，学生不仅巩固了除法计算，还对乘除法之间的联系、除法各部分之间的关系有了初步的理解，思维也得到了更进一步的锻炼，可谓一举多得。

二、智慧如“盐”，拒绝平淡

数学是思维的体操，数学思想正如菜肴中的“盐”。没有盐的菜平淡无味，没有智慧的数学课可谓味同嚼蜡。教师应该深入挖掘练习中所蕴藏的各种数学思想去引领学生，让学生在探索中获得感悟，让智慧之花在课堂尽情绽放。

案例2：“有趣的数阵”（一）（图1）

师：先计算，再比较上下两道算式，看看你有什么发现。

（学生很快便有了发现。）

生1：上下两题得数相等。

生2：上面的算式都是单数从小到大依次相加，下面算式的两个乘数都相同。

生3：我觉得从“1”开始有几个单数相加，就等于几乘几。比如有3个单数相加就等于3乘3。

师：再写几组，看看是不是跟刚才的发现相符。

生：1+3+5+7+9=25，5×5=25。1+3+5+7+9+11=36，6×6=36。……的确都相符。

师：这只是一个巧合呢，还是其中藏着什么奥秘？

（沉思了片刻后，有几个学生举手。）

生：不是巧合。我们可以把加法算式通过变形得到几个相同加数相加的算式。比如“1+3+5+7+9”中，“9”给“1”4个1，“7”给“3”2个1，它们就都可以变成5，也就是说1+3+5+7+9=5+5+5+5+5=5×5。

（其他学生也纷纷点头赞同。）

在上述案例的教学中，学生不仅进行了观察发现，学会了归纳概括，还展开了深入的分析，找到了现象背后的原因，并在此过程中应用了“移多补少”“转化”等数学思想方法，体会到了数学独有的严谨性、深刻性。

三、以“图”作“酱”，色香俱全

形象的内容总能吸引儿童，精美的画面也总能感染儿童。图形与空间的一些内容以及数形结合的思想，常常能带给儿童美的享受与震撼，就像给菜肴带来色、味双重变化的“酱”。教师在练习中合理使用各种“图”，不仅能帮助学生理解相关内容，还能让学生体会到“数”与“形”之间的内在联系，感受到数学独特的美。

案例3：“有趣的数阵”（二）

1+3=2×2

1+3+5=3×3

1+3+5+7=4×4

1+3+5+7+9=5×5

1+3+5+7+9+11=6×6

……

师：刚才大家的发现还可以用一个有趣的图形来表示（先出示塔状图），只要将图中的点子巧妙地移一移，就可以变形成为一个方阵。谁来试一试？（再引导学生逐步变形成为右边的方阵图）（图2）

生1：左边的点子是横着排的，右边的点子是拐弯排的。

生2：其实每排的点子是一样多的，所以总数相等。

生3：左边好像是金字塔，右边好像是正方形。

生4：还可以一直继续排下去。

生5：真神奇呀！

……

一句“真神奇呀！”是学生内心由衷的感叹。他们为数学之神奇久久折服，被数学之美深深感动，而这种感动必然成为学生进一步学习和探索的不竭动力。

四、挑战似“醋”，增进食欲

好似“醋”能开胃，使人食欲增强，富有挑战性的学习内容也对儿童有着独特的吸引力，能强烈地激发学生的求知欲和成就感。所以，练习不仅要紧扣基础，还要做到层层递进、逐步提升，让学生在不断地挑战中提高能力、获得自信，求知欲望越来越强。

案例4：“做蛋糕”（图3）

师：看，有几个美味的大蛋糕正等着我们来享用！我们吃蛋糕是按什么顺序吃的？

生：从上往下。

师：请你按照从上往下的顺序来完成每组计算，再想一想一个大蛋糕里的三层算式有什么联系。

生1：最下面一层算式的计算过程和上面两层一样。

生2：把上面两层的算式合起来就是最下面一层的算式。

师：是的，两步计算的算式就是由两道一步计算的算式组合而成的。刚才我们吃过了美味的蛋糕，还发现了蛋糕中的“秘密”。现在请你来“挑蛋糕”，看看选用哪些小蛋糕能做成3层的大蛋糕。（出示以下几组算式，如图4）

生：2×4和8×9两个小蛋糕可以合成一个大蛋糕2×4×9。24÷4和6×3可以合成24÷4×3。6×3和18÷2还可以合成6×3÷2。

师：为什么不选7×5这个算式？选的时候要注意什么？

生：7×5这个算式跟其他算式没有关系。只有这个算式里的一个数是另一个算式的得数时，这两个算式才能合成一道算式。

师：的确如此。那你们能自己独立做一个三层的大蛋糕吗？

生：能。……

从“吃蛋糕”到“挑蛋糕”，再到“做蛋糕”，要求层层递进却又很有趣，挑战不断出现但并不繁难。学生的学习热情始终高涨，对这类两步计算题的运算顺序、结构特点的认知也逐步深入。更可贵的是，他们在挑战中发挥了潜能、获得了自信，在自我构建中加速成长。

实践证明，这样的教学设计在落实了双基的同时，更加凸显了学生的主体地位，更加关注了学生的情感态度，帮助学生更好地积累了数学活动的经验，而且也促进了学生对数学思想的感悟。子曰：“好之者不如乐之者。”如此“色香味”俱全的数学大餐，怎能不让学生如痴如醉、乐在其中！