一道教材例题的变式教学

曾妙云

（广东省惠州市惠阳区第四中学）

一道教材例题的变式教学

曾妙云

（广东省惠州市惠阳区第四中学）

变式教学是我国教学研究者提出的一种教学方法，变式教学不单是解决一个问题，还能解决一类问题，为学生的知识经验及思想方法迁移提供了良好的活动平台.人教版《义务教育教科书·数学》中，三角形的角平分线是用全等三角形知识研究的第一类几何图形，其例题设置具有典型性，它与全等三角形、角平分线、内心等内容相关联，进行变式教学，对建立知识之间的联系，改善后续学习，具有实践意义.

角平分线；变式教学；知识经验

一、源题分析

1.源题

选自人教版《义务教育教科书·数学》八年级上册“12.3角的平分线的性质”第50页的例题.

题目如图1,△ABC的角平分线BM，CN相交于点P.求证：点P到三边AB，BC，CA的距离相等.

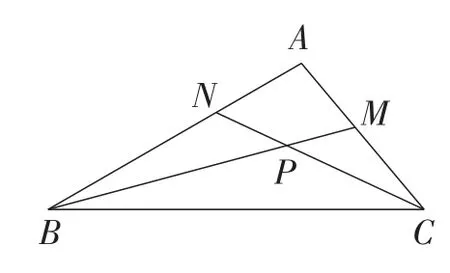
图1

图2

证明：如图2，过点P作PD，PE，PF分别垂直于AB，BC，CA，垂足分别为点D，E，F.

因为BM是△ABC的角平分线，点P在BM上，

所以PD=PE.

同理，PE=PF.

所以PD=PE=PF，

即点P到三边AB，BC，CA的距离相等.

2.源题考查目标

（1）应用角平分线的性质解决问题，当问题中涉及角的平分线时，就相当于已知一组线段（角平分线上的点到角两边的垂线段）相等，这也为证明线段相等提供了一种途径；（2）等式的传递性；（3）作辅助线的方法.

3.知识关联

此题有承上启下的作用，它既是对上一章“三角形的三条角平分线交于一点”的进一步阐述，为下一章学习垂直平分线提供方法指导，又是对九年级三角形内心知识的提前渗透，其中辅助线的作法也是解决角平分线问题的关键.

二、变式题及点评

1.设置新的问题情境，活用巧用

变式1：三条公路把A，B，C三个小区连成一个三角形区域，淡水城区决定在这个三角形区域内修建一个超市，要使超市到三条公路的距离相等，则这个超市应该建在（）.

（A）在AC，BC两边高线的交点处

（B）在AC，BC两边中线的交点处

（C）在∠A，∠B两内角平分线的交点处

（D）在AC，BC两边垂直平分线的交点处

【点评】变式1选取了学生最易接受的现实情境，变远离现实为回归生活，目的是让学生明白数学源于生活，又应用于生活的理念，很好地激发学生学习的兴趣与热情.

2.条件与结论的“变”与“不变”

变式2：如图3，△ABC的角平分线BM，CN相交于点P，求证：点P在∠A的平分线上.

图3

【点评】条件不变，结论变换为求证点P在∠A的平分线上.实际上变式2是比源题深入一步，要求学生进一步应用角平分线的判定，解题思路与源题如出一辄，让学生进一步思考三角形三条角平分线的特征及与三角形三边的关系.

变式3：如图4，已知△ABC的∠ABC的平分线BM和∠BCA的外角平分线CN相交于点P，求证：点P到三边AB，BC，CA所在直线的距离相等.

【点评】变换条件，结论不变.条件从两条内角平分线变为一条内角平分线，另一条为外角平分线，如此改变会不会改变角平分线交点到三边所在直线的距离关系呢？引起学生进一步思索与探讨.

变式4：如图5，已知△ABC的外角∠CBD和∠BCE的平分线相交于点P，求证：点P在∠BAC的平分线上．

【点评】条件变换，结论变换.条件从两条内角平分线变为两条外角平分线，结论变为求点P在∠BAC的平分线上.题设与结论都改变，但解题方式与思想大同小异，作辅助线的方法是解决角平分线问题时常用的方法.此种方法学生应做到举一反三、熟练掌握.

3.变式的巧妙

变式5：如图6，△ABC的角平分线BM，CN相交于点P，且AB，BC，CA三边的长分别为7，10，6.

（1）求证：点P到三边AB，BC，CA的距离相等.

图4

图5

图6

（2）连接AP，则S△ABP∶S△BCP∶S△CAP等于多少？

【点评】赋以数值，给予线段量化，通过推导形象得出“三条角平分线把一个三角形分成三个三角形的面积比与其底边成正比”这一重要结论.

变式6：（2012年广东·珠海卷）如图7，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．

（1）用尺规作图方法，作∠ADC的平分线DN（保留作图痕迹，不写作法和证明）；

（2）设DN与AM交于点F，判断△ADF的形状（只写结果）．

【点评】条件衍变，结论呈新.变式考查了尺规作图，培养了学生的动手操作能力.结合三角形的三线合一形成“一内角一外角”的角平分线，与源题有异曲同工之妙，类型比源题更具有开放性，考查方向多样化.

图7

三、对变式教学的思考

通过对教材例题的变式，从设置真实的生活情境开始，让学生产生对数学的学习兴趣.相同内容，不同形式的转换，考查类似的内容，让学生做到举一反三，熟练掌握角平分线的性质，体会辅助线的妙用.通过运用类比、转化、数形结合等数学思想，让学生明白知识的获得，是用已知的方法去探究未知的世界的过程.数学课堂上的变式教学是连接“四基”与创新的纽带.通过变式教学，有意识地引导学生从“变”的现象中发现“不变”的本质，从“不变”的本质中探求“变”的规律，使知识点融会贯通，逐步培养学生灵活多变的思维品质，增强其应变能力，让学生的变式发散思维得以拓展.

［1］钱德春.类比教学，我们应该关注什么？［J］.中学数学教学参考（中旬），2015（8）：14-16.

［2］张惠添.变式教学在初中数学教学中的应用探究［D］.广州：广州大学，2012.

［3］王宝仓，高庆军.点评：渗透分类讨论感悟类比思想［J］.中学数学教学参考，2015（5）：23-25.

2017—09—12

曾妙云（1982—），女，中学一级教师，主要从事中学数学基础教育方面的研究.