一课三磨，磨出课堂精彩——“平均数”教学实践与反思

何勇明

（浙江省杭州市余杭区安吉路良渚实验学校）

一课三磨，磨出课堂精彩
——“平均数”教学实践与反思

何勇明

（浙江省杭州市余杭区安吉路良渚实验学校）

通过一课三磨，教师设计出匹配当下学生学情的学习素材，以及不断改进课堂教法，从而调动学生学习的积极性.同时，帮助学生掌握平均数的计算方法和理解“权”的意义，使学生真正理解统计的思想方法.

平均数；教学反思；课堂精彩

笔者曾有幸承担了初中数学一节校级公开课，执教浙教版《义务教育教科书·数学》八年级下册“3.1平均数”.回望这一段历程，从备课、磨课，到不断改进教学，上完公开课，收获颇多.文章以“平均数”一节的三次课堂教学实践为线索，对学习素材的改进、教法的改进，以及学生学习积极性的激发等方面进行实践和反思.

教学目标：

（1）理解平均数和加权平均数的概念；

（2）会计算平均数和加权平均数；

（3）会用样本的平均数来估计总体的平均数.

重点：加权平均数的计算.

难点：对“权重”的理解对学生来说有一定的难度.

一、第一次试教

环节1：引出新知.

师：同学们，今天我们将要学习新的知识，先看看下面的问题.

题目某果农种植的100棵苹果树即将收获，果品公司需要对总产量进行估计.

（1）果农随机摘下20个苹果，称得这20个苹果的总重量为4千克，这20个苹果平均重量是多少？

（2）果农从100棵苹果树中随机选出10棵苹果树，数出树上苹果的个数，得到以下数据（单位：个）：154，150，155，155，159，150，152，155，153，157.你能估计出平均每棵树苹果的个数吗？

（3）根据（1）（2）你能估计出这100棵苹果树的苹果总产量吗？

环节2：巩固概念.

练一练：统计一名射击运动员在某次训练中10次射击的中靶数，获得如下数据（单位：环）：7，9，10，9，10，7，9，8，9，10，求这次训练中运动员射击的平均成绩.

环节3：例题学习.

例某校在一次广播操比赛中，801班、802班、803班的各项得分（满分100分）如表1所示.

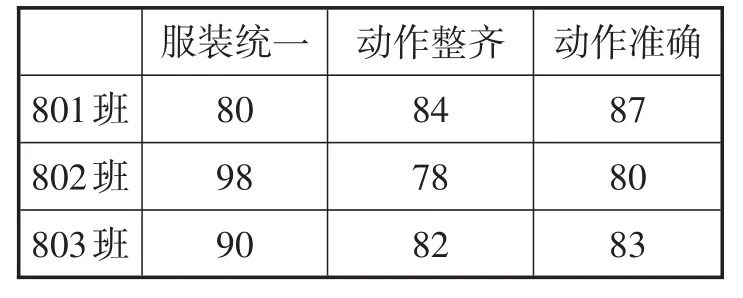
表1

（1）如果根据三项得分的平均分从高到低确定名次，那么三个班的排名顺序是怎样的？

（2）如果学校认为这三个项目的重要程度有所不同，而给予“服装统一”“动作整体”“动作准确”三个项目在总分中占的百分比分别是15%，35%，50%，那三个班的排名顺序又怎样？

环节4：课堂小结.

略.

师生反馈

师1:“平均数”这节课小学已经学过，内容上是否有重叠，小学与初中知识衔接点在哪里？

师2：课堂的气氛太沉闷了，教师讲得太多，学生的积极性好像没有被真正调动起来.

师3：引入部分时间太长，数据太复杂，最好选用是学生熟悉的素材引入.

生1：好像那个“权”不太懂.

生2：平均数以前学过的，很多不用讲.

执教者反思

教师和学生的反馈如当头一棒，令笔者羞愧难当.主要是以下几个方面的问题.

第一，教学观念陈旧.一直以为教师只要把知识点讲清楚就算是不错的课了，总是把方方面面预设好教给学生就好了，却忽视了对学生学习积极性的调动和兴趣的培养.

第二，对重、难点没有突破.这节课的重、难点是加权平均数的求法，以及对“权”的理解，在教材中有这样一个结论，“权”越大，对平均数的影响就越大，这个难点如何去突破？

第三，没有把握好学情.在小学学生已经学过平均数，新课要放在增量知识上，特别是教师要设计好的学习素材去突破难点.

二、第二次试教

环节1：引出新知.

师：同学们，我们来看这样一个问题.

题目眼下正是桔子丰收的季节，某果农种了100棵桔子树，他想要估计今年的总产量，先从100棵桔子树上随机选出10棵桔子树，数出树上的桔子，得到以下数据（单位：个）：208，195，210，210，218，195，208，210，206，210，试帮忙计算这10棵桔子树平均每棵树结桔子的个数.快速计算一下.

【设计意图】第一，引例中的苹果树这里的学生不熟悉，宜改为学生较熟悉的桔子树，而且眼下正是桔子丰收期，更接学生“地气”；第二，10棵苹果树上苹果个数的数据在某个数波动不明显，对“基准法”求平均数学生不易发现，故对试教题目中苹果个数数据进行重新设计.

环节2：巩固概念.

练一练：统计一名射击运动员在某次训练中10次射击的中靶数，获得如下数据（单位：环）：7，9，10，9，10，7,9，8，9，10.求这次训练中运动员射击的平均成绩.

变式1：上题中运动员的中靶数如表2所示，怎样求这次训练中运动员射击的平均成绩？

表2

变式2：若该运动员重新射击10次的中靶数如表3所示，求该运动员这10次射击的平均成绩.

表3

【设计意图】在第一次试教中是没有变式的，这里“权”指的是每发成绩（环）出现的次数，变式1将数据进行表格化处理，考查学生知识的迁移能力，变式2改变“权”的大小，可以让学生初步理解“权重”.

环节3：例题学习.

例学校招聘校园广播台播音员，对A，B，C三名候选人进行了三项素质测试，成绩如表4所示.

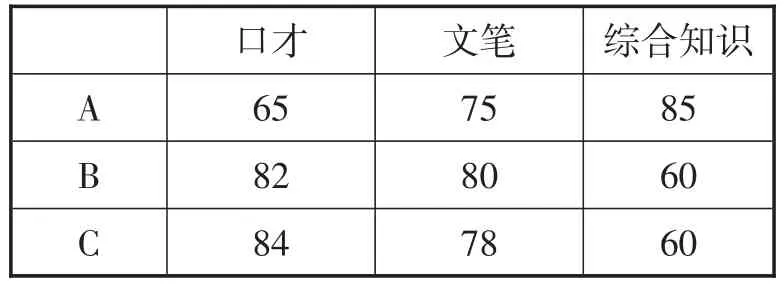
表4

（1）方案1：如果按照平均成绩录取，会录取谁？如果你是负责招聘的老师，此方案你满意吗？为什么？

（2）方案2：校团支书把口才、文笔、综合知识得分按照50%，30%，20%的比例进行排序，会录取谁？为什么？

【设计意图】笔者取材学生身边的资源，重新设计了例题，在第一次试教中例题的第（1）小题只是纯粹计算平均数，没有考虑到平均数一致的情况下谁更优秀.这样的问题设计，学生可以更好地对“权重”进行理解.

专家反馈

第二次试教后，有教师提出质疑，这是一节概率统计中的平均数新课，许多教师把概率统计中的课上成了计算课，只是培养了学生的计算能力，没有真正落实概率统计的思想方法.另外，学生对教学难点“权”的理解还不够清楚，要进一步分解难点.省教研员提出，一堂好课要有知识的增量，课堂教学要把学生的学习积极性调动起来，培养学生的学习兴趣，要去研究学生如何学.

三、公开课教学

环节1：创设情境引出新知.

师：同学们，今天我们的课题是什么？

教师课前放映幻灯片，展示课题“平均数”.

生：平均数.

师：平均数以前学过吗？

生：学过.

师：以前学的平均数是怎么样的？

生1：平均数就是将一堆东西平均分配给几个人.

师：平均数怎么计算的？

生2：用总量除以个数.

师：很好，那么今天又要学习平均数，猜猜看会哪里不一样？

生3：可能计算平均数的方法不一样.

生4：是不是有平均数的应用题？

师：好，带着这样的疑问，我们走进今天的课堂，先来看下面这道题目.

题目学校食堂新鲜的桔子来自某果园，某果农种了100棵桔子树，他想要估计这100棵桔子树的总产量.你能帮他想个办法吗？

生5：先取一些桔子称一下，得到每个桔子有多重，然后找几棵树，数出上面的桔子数，再去估算一下.

师：那么这些桔子怎么取，树又怎么找有要求吗？

生5：要随机取.

师：为什么要随机取？

生5：因为不同地方会有不一样桔子.

师：不错，要保证公平，班里小慧同学是这样估算的：她随机取了20个桔子，称得总质量为2千克.又从100棵桔子树上随机选出10棵桔子树，数出树上的桔子，得到以下数据（单位：个）：208，195，210，210，218，195，208，210，206，210.你能帮她估计总产量吗？

环节2：同上.

环节3：拓展提升.

合作探究：“十一”期间，联华超市为了满足不同顾客的需求，现把单价为15元/千克的甲种糖果和单价为10元/千克的乙种糖果混合销售.表5是几种混合方案.

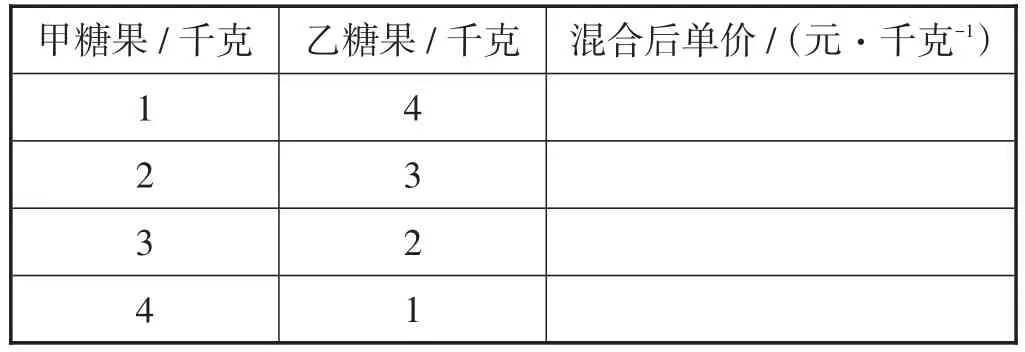
表5

（1）试计算混合后的单价.

（2）观察混合后单价变化和甲、乙糖果数量变化，你发现了什么？

（3）“权”对平均数有什么影响？

【设计意图】为了分化权越大对平均数的影响就越大这一新知难点，增设环节3的合作探究题.通过小组合作学习，学生最后发现糖果的千克数就是“权重”，权越大，对平均数的影响也越大，从而让学生进一步理解“权重”对平均数的影响.

环节4：例题学习.

例题同第一次执教，增加第（3）小题：如果你是负责录取的老师，既要突出口才，又要把文笔和综合知识放在同等重要的地位，如何修改方案？

【设计意图】这样设问一下子把学生的思维打开了，不仅让学生再次体验权重对平均数的影响，而且我们可以赋予权新的意义，真正活学活用了统计思想方法.

四、教后反思

通过三次教学，笔者认为教师上好一堂课应从如下几个方面去修炼.

第一，要理解教材，精准把握教材中的重、难点.新课的重、难点是整节课的主心骨，不能偏离，而教材只是知识的载体，教师要会处理和加工教材，设计出符合自己学生学情的学习素材.例如，“平均数”教学中引例和例题的设计，以及对权重、难点知识的设计，要会创设合适情境和搭梯子去分化难点知识.教师还要重视教材的整体性作用，特别是初小衔接.在“平均数”这节课中，在小学学生基本掌握平均数的计算方法，初中又学平均数，知识的增量要放在加权平均数，以及对“权”的理解上.教师还要注重教学中数学思想方法的落实，“平均数”一课从表面看就是计算，但从本质看是对统计思想的渗透，所以教师要善于引导学生感悟题目背后的数学思想方法，真正把握数学的本质.

第二，要理解学生.课前教师要了解学生知识的起点在哪里，要在这个基础上再去设计课堂，可以充分提高课堂的效率.另外，教师要知晓学生感兴趣的是什么，在课堂上教师要设计出学生感兴趣的问题，因势利导，激发其学习的积极性.

第三，教师要改进教法.过去，教师总是站在自己的角度研究怎么教，而忽视了学生怎么学.《义务教育数学课程标准（2011年版）》明确指出，学习要以生为本、以学促教，培养学生的学习兴趣.所以，教师要改变固有的观念，多去研究如何去引导学生更好的学.

一课三磨，不是简单的一种教学反思，它是教师一个再创造的过程，它“磨”出的是教师的专业成长，“磨”出的是教师的智慧.教师只有对课堂不断的实践和反思，才会绽放真正的课堂精彩.

［1］刘军.浅谈如何上好一节课［J］.教改教法,2014（2）：30-31.

2017—09—08

何勇明（1978—），男，中学一级教师，国家二级心理咨询师，主要从事初中数学教学研究.