多角度探究2017年天津市中考网格作图题

贯忠喜，陈健

（天津市东丽区教师进修学校；天津市河东区教育中心）

多角度探究2017年天津市中考网格作图题

贯忠喜，陈健

（天津市东丽区教师进修学校；天津市河东区教育中心）

文章从“寻源头，深挖教材得真题”“探解法，不同思维求发展”“思内涵，潜在功能助教学”等方面对2017年天津市中考“网格作图题”予以探究，意在将类似问题的思考从更多方面与同行探讨与交流，以引起大家的思考，更好地为学生发展服务.

网格作图；尺规作图；解法研究

题目（2017年天津卷第18题）如图1，在每个小正方形的边长为1的网格中，A，B，C均为格点.

（1）AB的长度等于____；

（2）在△ABC内部有一点P，满足S△PAB∶S△PBC∶S△PCA=1∶2∶3，试在如图1所示的网格中，借助无刻度的直尺画出点P，并简要说明你是怎么画出来的.

从以往天津市中考网格作图题来看，历年来的天津市中考网格作图题都独树一帜，题目虽小但却蕴含着巨大的思维和研究空间，为教师日后教学和研究提供了极好的素材.2017年天津市中考网格作图题，题目仍然保持了内涵深刻、形式简洁、立意深远的特点，下面从不同角度对该题进行探究.

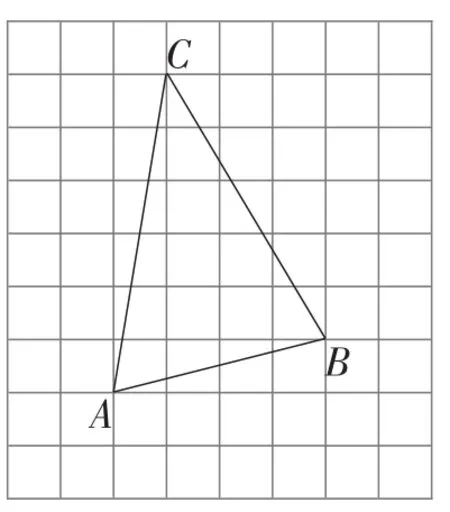
图1

一、寻源头，深挖教材得真题

人教版《义务教育教科书·数学》八年级下册第50页练习第7题：如图2，直线l1∥l2，△ABC与△DBC的面积相等吗？为什么？你还能画出一些与△ABC面积相等的三角形吗？

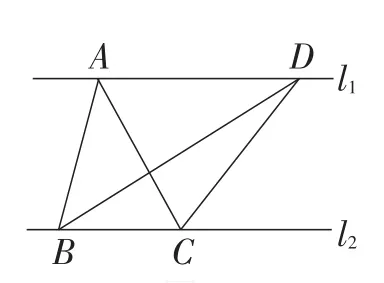
图2

显然，△ABC与△DBC的面积是相等的，理由是：我们可以设l1与l2之间的距离为h，并设BC=a，则△ABC与△DBC的面积都等于同时，若在直线l1上任意取一点P，然后连接PB，PC，那么△PBC的面积永远等于△ABC的面积.因为点P是直线l1上的任意一点，所以我们可以画出无数个与△ABC面积相等的三角形.

从教材原题的呈现形式看，它只是一个“同底等高的三角形面积相等”原理的简单运用问题，但当我们认真体会问题的本质，以及它与中考试题之间的内在联系时，会觉得一下子寻找到了“2017年天津市中考网格作图题”的源头活水，“蓦然回首，那人却在，灯火阑珊处”，其解题思路也会因此展开.

二、探解法，不同思维求发展

策略1：设点P满足题意，即点P为分别与△ABC两条边平行的直线的交点，根据条件画出这两条直线即可.

为叙述方便，我们给出下面的命题.

命题1：如图3，点D，E分别在边AB，AC上，DE∥BC，点P在DE上，若BD∶BA=a∶b，则S△PBC∶S△ABC=a∶b.

运用相似三角形性质和三角形面积公式容易证明该命题是真命题，这里不加赘述.

分析1：如图4，设AC分别与网格线HR，TY相交于点D，E，取格点F，连接FB并延长，得点M，N，连接EM，DN，EM与DN相交于点P，点P即为所求.

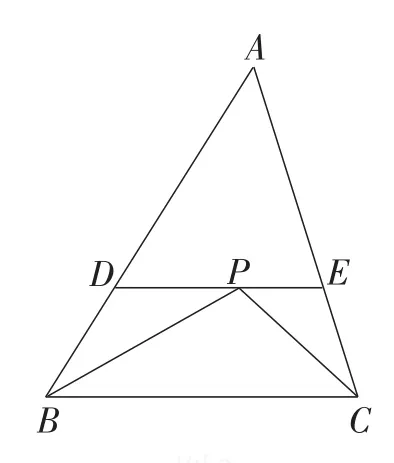
图3

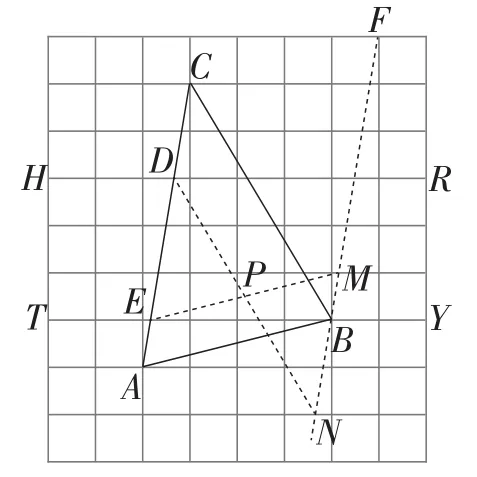
图4

解法1：由作图知FB∥AC.

因为横向网格线与纵向网格线都是各自平行的，

有MB=AE，CD=BN.

所以四边形AEMB，DCBN都是平行四边形.

所以EM∥AB，DN∥BC.

故此时点P满足条件.

分析2：如图5，取格点E，F，T，H，连接EF交BC于点G，连接TH，交AB于点R，AC与网格线相交于点D，AB与网格线相交于点N，连接DR，GN，它们相交于点P，点P即为所求.

解法2：由作图知，CE=BF.

又因为CE∥BF，

所以G为BC的中点.

由条件知，N为AB的中点.

故NG为△ABC的中位线.

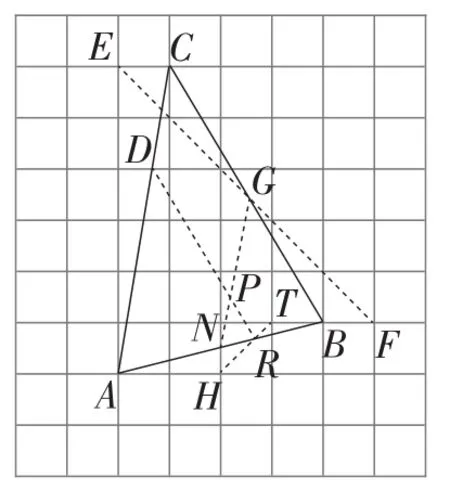
图5

所以点P一定在线段NG上.

因为TB∥AH，

所以DR∥AB.

所以点P一定在线段DR上.

故线段DR，GN的交点P即为所求.

分析3：如图6，取格点D，M，N，F，连接DF得点G，连接MN得点T，取AC与网格线交点E，AB与网格线交点H，连接HG，TE，HG，TE相交于点P，点P即为所求.

解法3：因为四边形CFBD为矩形，

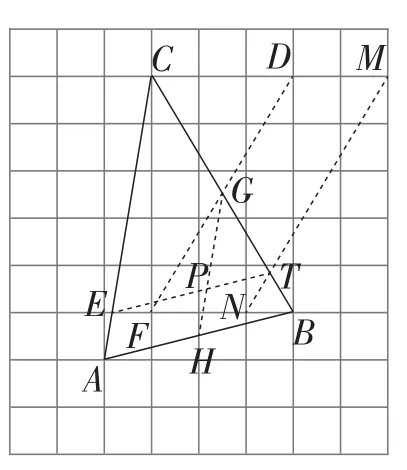
图6

所以G为BC的中点.

又因为H为AB的中点，

所以GH为△ABC的中位线.

所以HG∥AC.

所以ET∥AB.

故点P为满足条件的点.

策略2：由面积关系，确定射线AP，BP，CP与三边交点的准确位置，作出射线AP，BP，CP其中的两条，确定其与边的交点即可.

为说明该策略，我们给出如下命题.

命题2：如图7，点D在边BC上，P为AD上一点，

则S△PAB∶S△PAC=BD∶DC.

下面给出该命题的证明.

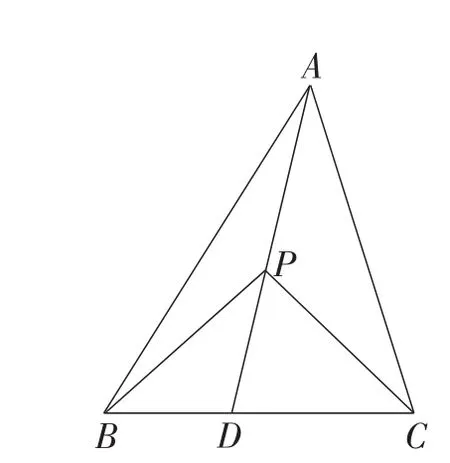
图7

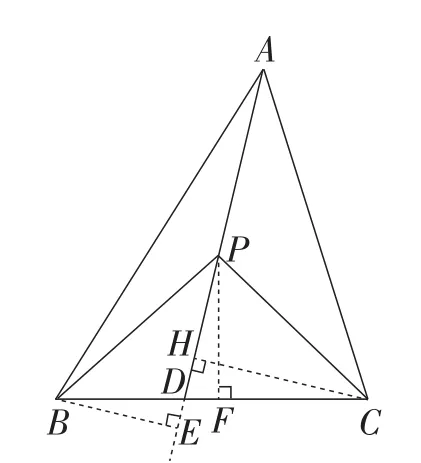
图8

证明：如图8，作BE⊥AD于点E，作CH⊥AD于点H，作PF⊥BC于点F，

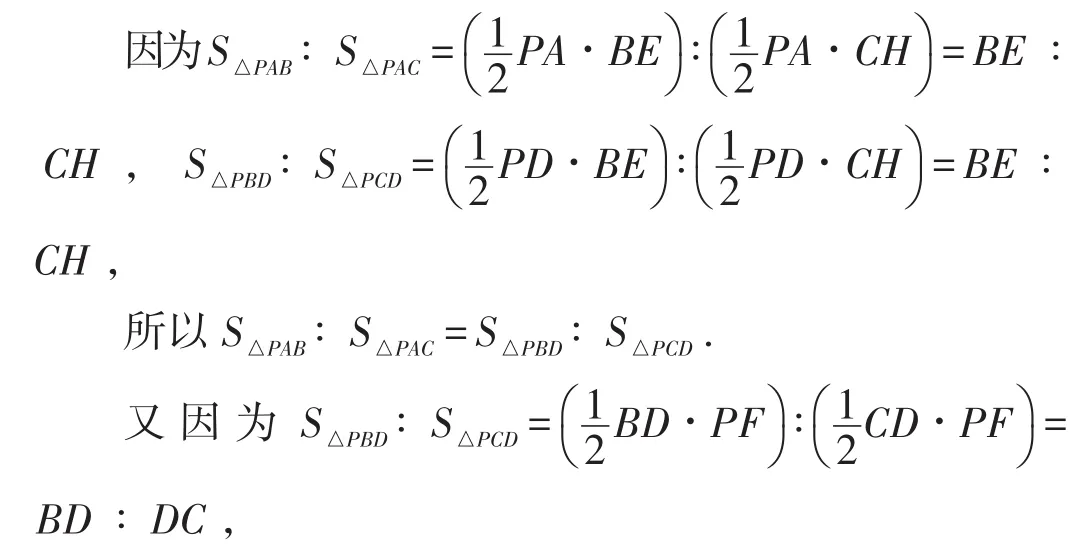
所以S△PAB∶S△PAC=BD∶DC.

下面我们就根据命题2给出一些解法.

分析4：如图9，取AC与网格线交点E，取格点M，N，连接MN，MN与AB相交于点H，连接BE，CH，BE与CH相交于点P，点P即为所求.

解法4：根据题意有AE∶EC=1∶2.

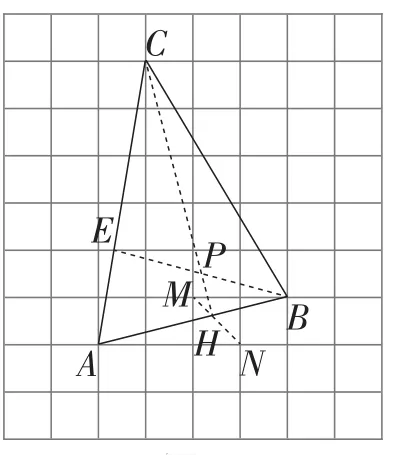
图9

因为BM∥AN，

所以BH∶HA=BM∶AN.

又因为BM∶AN=2∶3，

所以BH∶HA=2∶3，BE与CH相交于点P.

则由命题2，有S△PBA∶S△PBC=1∶2，S△PCB∶S△PCA=2∶3.

满足S△PAB∶S△PBC∶S△PCA=1∶2∶3.

所以点P即为所求.

分析5：如图10，取格点M，N，Q，R，连接QR，交BC于点D，连接MN，交AB于点H，连接AD，CH，AD与CH相交于点P，点P即为所求.

解法5：因为BM∥AN，

所以BH∶HA=BM∶AN.

而BM∶AN=2∶3，

所以BH∶HA=2∶3.

因为CQ∥BR，

所以BD∶DC=BR∶CQ.

而BR∶CQ=1∶3，

所以BD∶DC=1∶3.

因为AD与CH相交于点P，

由命题2有S△PCB∶S△PCA=2∶3，S△PAB∶S△PAC=1∶3，

满足S△PAB∶S△PBC∶S△PCA=1∶2∶3.

所以点P即为所求.

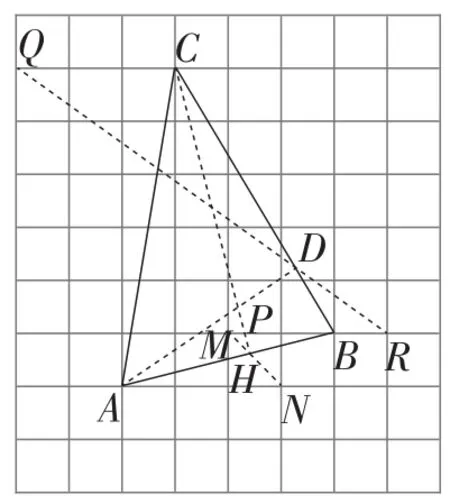
图10

分析6：如图11，取格点Q，R，连接QR，QR交BC于点D，AC与网格线相交于点E，连接AD，BE，AD与BE相交于点P，点P即为所求.

解法6：由题意有AE∶EC=1∶2.

因为CQ∥BR，

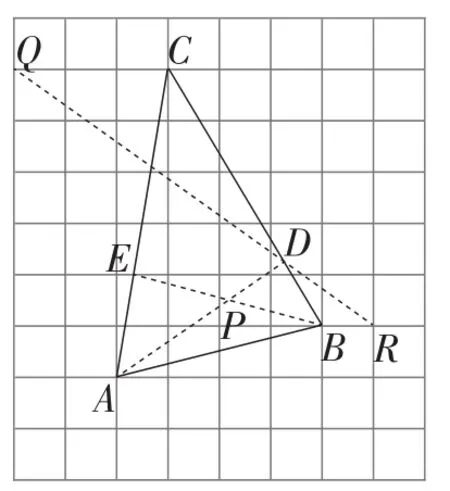
图11

所以BD∶DC=BR∶CQ.

而BR∶CQ=1∶3，

所以BD∶DC=1∶3.

又因为AD与BE相交于点P，

由命题2有S△PAB∶S△PBC=1∶2，S△PAB∶S△PCA=1∶3.

满足S△PAB∶S△PBC∶S△PCA=1∶2∶3.

所以点P即为所求.

策略3：建立平面直角坐标系，计算出点P的坐标，画出点P.

如图12，以点A为坐标原点，以横、纵网格线为x轴、y轴建立平面直角坐标系，容易计算又因为所以设点P到AB，CA的距离分别为d1，d2，故有又因为可以得由条件易得直线AB，CA的解析式分别为x-4y=0，6x-y=0.设点P的坐标为P(x0，y0)，从而由点到直线的距离公式得到

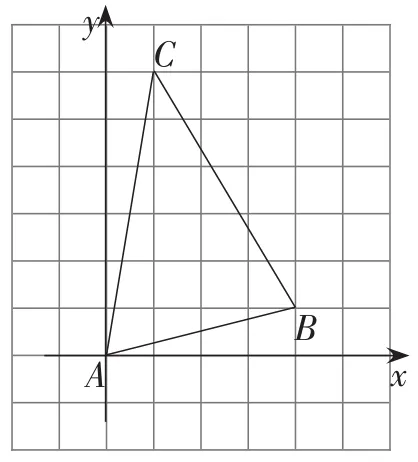
图12

分析7：如图13，取格点E，F，D，R，Q，连接EF得点M，连接BD得点N，连接MN，RQ，MN，RQ相交于点P，点P即为所求.

解法7：由作图知M，N分别为小正方形的中点，且线段MN上每个点的纵坐标都为设线段MN与网格线的一个交点为T，取格点H，

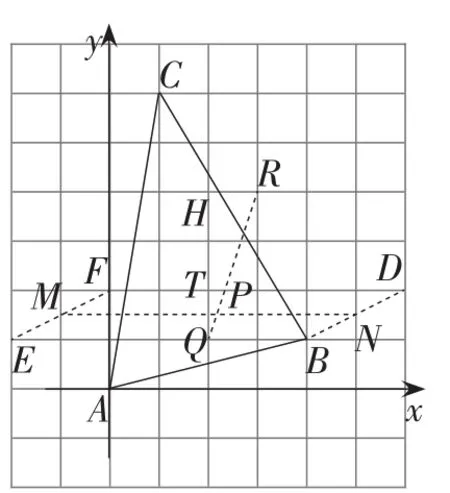
图13

因为PT∥RH，

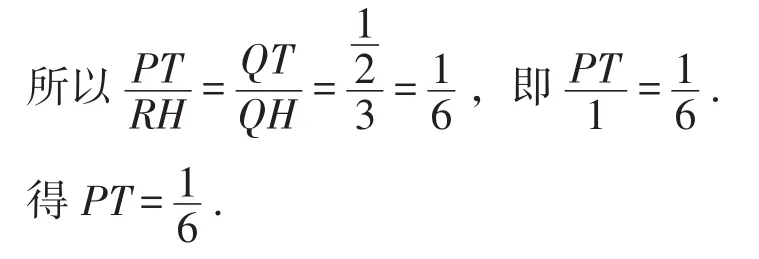
所以点P的坐标为故点P即为所求.

分析8：如图14，取格点M，F，D，E，连接MF，DE，MF与DE相交于点P，点P即为所求.

解法8：由作图知点P的纵坐标为

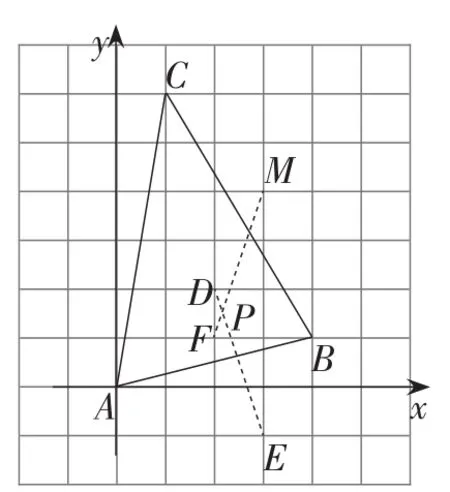
图14

设△PDF的DF边上的高为h1，△PEM的ME边上的高为h2，

易知△PDF∽△PEM.

因为h1+h2=1，

所以点P的坐标为故点P即为所求.

三、思内涵，潜在功能助教学

题目的解法研究暂告一段落，但对于试题本身而言，其所蕴涵的数学道理和数学思想还仍然深深地吸引着我们，我们不妨继续做如下思考.

思考1：在没有网格的状态下，任意△ABC内部若存在点P，满足S△PAB∶S△PBC∶S△PCA=m∶n∶p，其中m，n，p为互质的正整数，如何确定点P的位置？

其实解决这个问题并不困难，下面给出两种不同的画法.

画法1：运用命题1的思想.

如图15，首先在BC上用尺规作点M，N，使得BM∶MN∶NC=m∶n∶p，过点M作AB的平行线，过点N作AC的平行线，所作的两条平行线相交于点P，点P即为所求.

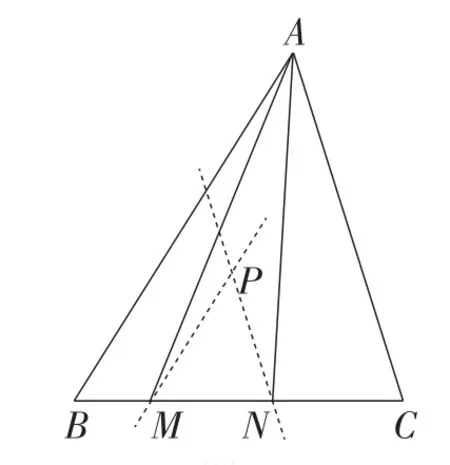
图15

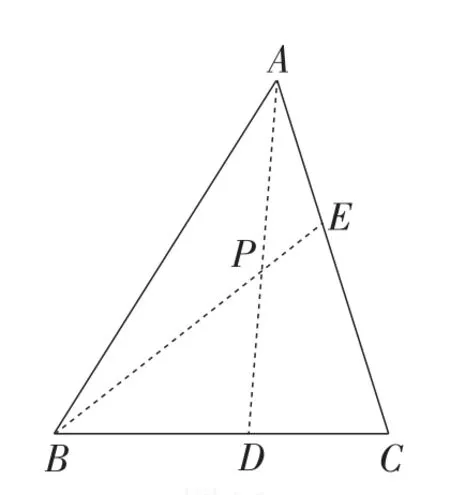
图16

画法2：运用命题2的思想.

如图16，用尺规在BC上作点D，使BD∶DC=m∶p，在AC上作点E，使AE∶EC=m∶n，连接AD，BE，AD与BE相交于点P，点P即为所求.

思考2：在没有网格的状态下，如图17，四边形ABCD内若存在一点P，满足S△PAB∶S△PBC∶S四边形PCDA=m∶n∶p，其中m，n p为互质的正整数，如何确定点P的位置？为解决该问题，需再给出一个命题.

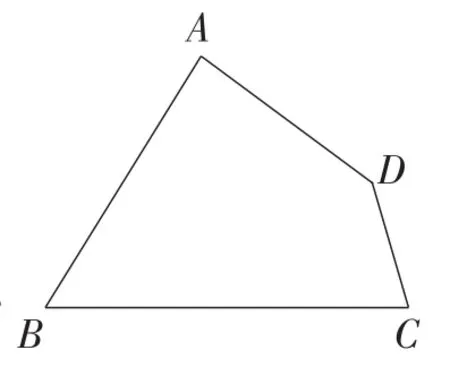
图17

命题3：如图18，AC，BD为四边形ABCD的对角线，点E，F在BD上，BE∶EF∶FD=m∶n∶p，分别过点E，F作AC的平行线，交BC于点M，N，则S△ABM∶S△AMN∶S四边形ANCD=m∶n∶p.

图18

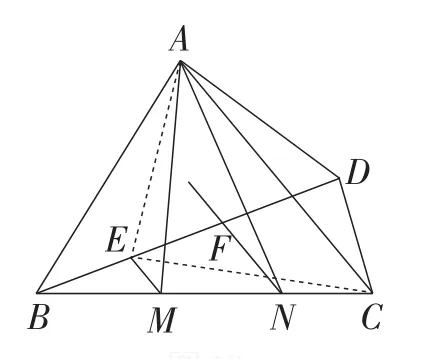
图19

下面给出该命题的证明.

证明：如图19，连接AE，CE，

因为BE∶EF∶FD=m∶n∶p，

因为S△ABE+S△CBE=S△ABE+S△BME+S△ECM，

又因为EM∥AC，

所以S△AEM=S△ECM.

用同样的方法，连接AF，CF，

所以S△ABM∶S△AMN∶S四边形ANCD=m∶n∶p.

下面我们给出思考2的作图过程.

如图20，连接AC，BD，在BD上取点E，F，使得BE∶EF∶FD=m∶n∶p.分别过点E，F作AC的平行线，交BC于点M，N，连接AM，AN，过点M作AB的平行线，交射线NF于点P，则点P即为所求.

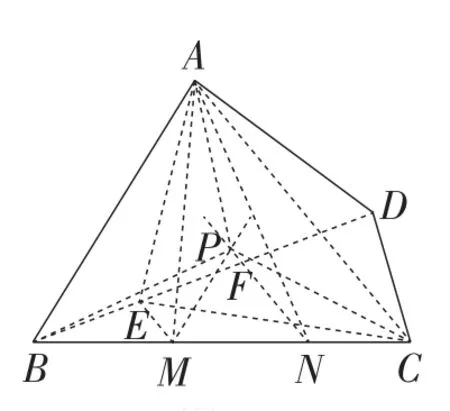
图20

证明：连接AP，BP，CP，

因为BE∶EF∶FD=m∶n∶p，

由题意和命题3，有S△ABM∶S△AMN∶S四边形ANCD=m∶n∶p.

因为MP∥AB，

所以S△PAB=S△ABM，S△PAM=S△PBM.

因为NP∥AC，

所以S△PAN=S△PCN.

所以S△PBC=S△AMN.

所以S△PAB∶S△PBC∶S四边形PCDA=m∶n∶p.

所以点P即为所求.

在欣赏和得意于“原题”与精彩的“通法”、陶醉于“以题解题”智慧的同时，我们发现，尺规作图需要对图形的几何性质了然于胸，在对图形中蕴含的几何性质不能掌握的情况下无法做到运用尺规作出需要的图形．通过坐标系研究平面图形，已经大大削弱了图形的几何特性，更多的解决几何问题的方式是采用解析法．网格背景下研究平面图形，一方面，保留了图形自身的几何特性，但由于是将图形放在了网格中，因此网格自身的位置及数量特性赋予了图形一些特殊关系，进而使图形的一般几何性质，得以特殊化、数量化；另一方面，网格又具有坐标的特性，可以根据图形特点及运算需要，在网格中任意建立坐标系．

网格背景下的作图，给了学生多角度探究的空间，而且由于构图时可以选用网格中的特殊点，为学生通过不同方式达到发现问题结论，进而通过计算进行作图提供了可能．作为一道评价学生学习程度的中考试题，其以学生的学习经验为基础，在短时间通过实验能够完成问题的分析与解决，并根据学生自身能力及特点，可以展现不同水平、不同角度的问题解决的方式.由此可见，这道网格背景下的作图题，有潜在的庞大功能，期待在教学中得以淋漓尽致的发挥．

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会．《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］刘金英.2010年中考数学试题分类解析（二）：空间与图形［J］.中国数学教育（初中版），2011（1/2）：46-57.

［4］贯忠喜.行云流水大气天成：浅议一道中考试题的教学导向功能［J］.中国数学教育（初中版），2014（6）：46-53.

2017—08—19

贯忠喜（1965—），男，中学高级教师，主要从事初中数学教学及评价研究.