对一道几何问题的研究与拓展

李发勇

（四川省巴中市巴州区大和初中）

对一道几何问题的研究与拓展

李发勇

（四川省巴中市巴州区大和初中）

常见的问题研究误区有就题论题、偏重方法记忆和缺少具体技能应用，缺乏数学思考.通过对一道几何题的一题多解、变式、拓展探究开发习题的潜在价值.

一题多解；变式拓展；潜在价值

问题是数学的心脏.对问题进行研究是数学教师的一项基本功，可以从不同视觉、功能和目的等方面入手开展研究，获得丰富的教学资源，促进自身专业的进步.文章通过一题多解，改变题目的条件，探求题目的结论，改变情境等多种途径，对问题进行多角度、多层次的理解，开发习题的潜在教学价值.下面以一道几何习题为例进行相关探究.

题目如图1，点D是等腰三角形ABC底边BC上一点，点E，F分别在AB，AC边上，且∠ADE=∠B，∠ADF=∠C.求证：BE=CF.

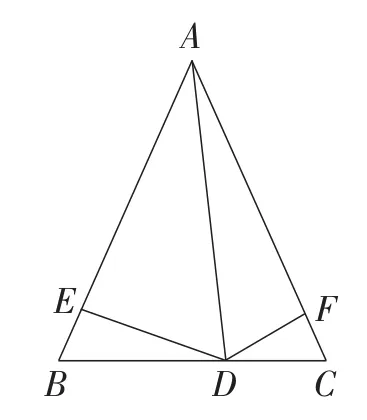
图1

一、证法探索

解题离不开审题，正确审题是解题的基础和前提.对于几何综合题，审题力争做到一审条件挖隐含，二审结论会转换，三审图形看特点，四审结构寻方法，从而突破思维障碍.

（1）从已知条件看，∠ADE=∠B=∠ADF=∠C，由相等角你会想到什么呢？通常会想到全等、相似、角平分线，等等.

（2）从结论看，要证明BE=CF，由于AB=AC，只需证明AE=AF即可.由相等线段你会想到什么？通常运用等角对等边，角平分线性质定理，全等三角形，等量代换，等边对等角去证明，等等.

二、一题多证

通过题目的一题多解，比较和评价不同的证法，总结解题思路，开阔视野，培养学生几何直观和推理能力等核心素养.

思路1：（1）从相等的角度想到相似.

①利用“一线三等角”模型的基本图形：如图2，当∠ABC=∠ACE=∠CDE时，因为∠ACD=∠ACE+∠ECD=∠A+∠ABC，所以∠A=∠ECD.从而有△ABC∽△CDE.

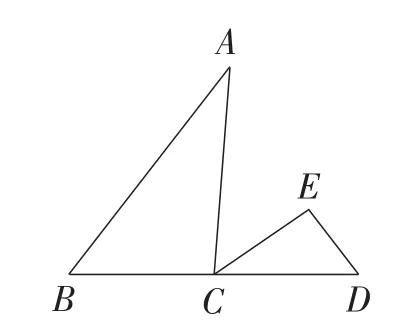
图2

再看题目的条件，由于∠B=∠ADE=∠C或∠B=∠ADF=∠C，获得两组基本图形，通过证明三角形相似，获得证明.

证明：（方法1）如图1，因为AB=AC，

所以∠B=∠C.

由∠ADB=∠C+∠CAD=∠ADE+∠BDE，

得∠BDE=∠CAD.

所以△BDE∽△CAD.

同理，△CDF∽△BAD.

由①②，推得BE=CF.

②利用三角形相似判定.

（方法2）如图1，由于∠ADE=∠B，又因为∠DAE=∠BAD，

所以△ADE∽△ABD.

同理，得△ADF∽△ACD.

所以AD2=AF·AC.②

因为AB=AC，由①②，得AE=AF.

则BE=CF.

（2）从相等角的角度想到全等.

分析：由于∠ADE=∠B或∠ADF=∠C，构造以∠ADE或∠ADF为底的等腰三角形，最后由三角形全等获证.

（方法3）如图3，以点A为圆心，AD长为半径画圆弧，交DE延长线于点G.

因为AG=AD，

所以∠G=∠ADE.

因为AB=AC，

所以∠B=∠C.

又因为∠ADE=∠B，

所以△ADG∽△ABC.

得∠GAD=∠BAC.

进一步，∠GAE=∠DAC.

又因为∠G=∠ADF，

所以△AEG≌△AFD.

所以AE=AF.

所以BE=CF.

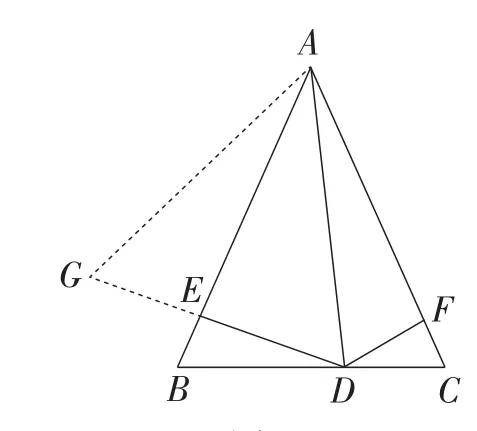
图3

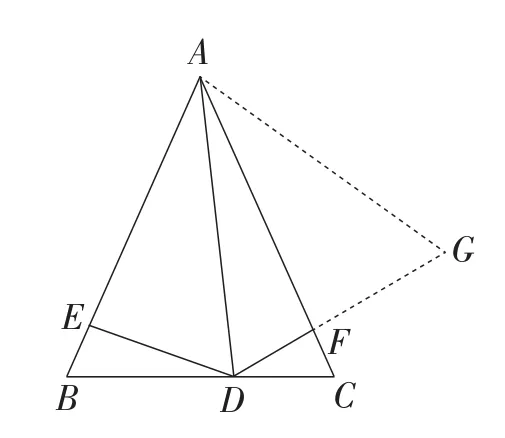
图4

思考1：如图4，如果以点A为圆心，AD长为半径画圆弧，交DF延长线于点G呢？同理可证.

（3）从相等角的角度想到角平分线.

分析：根据题目条件，易得∠ADE=∠ADF，即AD平分∠EDF.

①利用角平分线构造全等图形，最后，利用等腰三角形判定定理获证.

（方法4）如图5，在DE上截取DG，使DG=DF.

因为AB=AC，

所以∠B=∠C.

又∠1=∠B，∠2=∠C，

则∠1=∠2.

易证△ADG≌△ADF.

所以AG=AF，∠AGD=∠AFD.

所以∠AGE=∠CFD.

又因为∠AEG=∠B+∠BDE=∠1+∠BDE=∠ADB，∠CFD=∠2+∠DAF=∠C+∠DAF=∠ADB，

所以∠AEG=∠CFD.

得∠AEG=∠AGE.

所以AE=AG.

得AE=AF.

所以BE=CF.

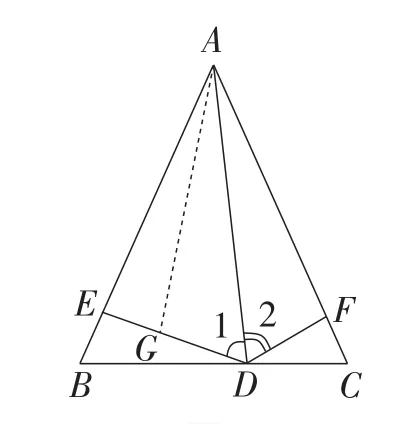
图5

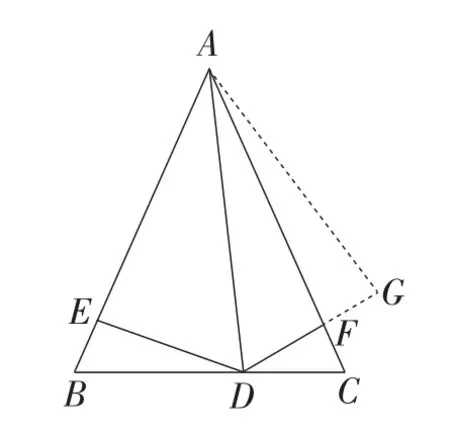
图6

思考2：如图6，如果延长DF至点G，使DG=DE呢？同理可证.

②利用角平分线构造角平分线性质定理图形，最后，通过全等获证.

（方法5）如图7，因为AB=AC，

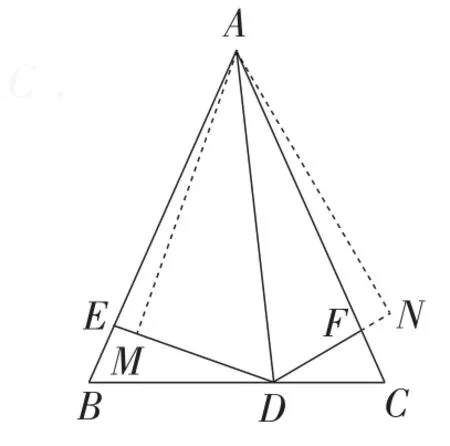
图7

所以∠B=∠C.

所以∠ADE=∠ADF.

过点A分别作AM⊥DE交DE于点M，AN⊥DN，交DF的延长线于点N，

所以AM=AN.

又因为∠AME=∠ANF=90°，

∠AEM=∠B+∠BDE=∠ADE+∠BDE=∠ADB，

∠AFN=∠ADF+∠DAC=∠C+∠DAC=∠ADB.

所以∠AEM=∠AFN.

所以△AME≌△ANF.

所以AE=AF.

所以BE=CF.

思路2：（1）从相等线段想到旋转.

（方法6）如图8，因为AB=AC，

所以将△ACD绕点A旋转至△ABG，使AB和AC重合，连接DG，

则△ABG≌△ACD.

又∠BAG=∠CAD，

得∠DAG=∠BAC.

进一步，得∠ADG=∠ABC=∠ADE.

所以点E在DG上.

又∠BEG=∠ABC+∠BDE=∠ADE+∠BDE=∠ADB，

∠CFD=∠DAF+∠ADF=∠C+∠DAC=∠ADB，

所以∠BEG=∠CFD.

所以△BEG≌△CFD.

所以BE=CF.

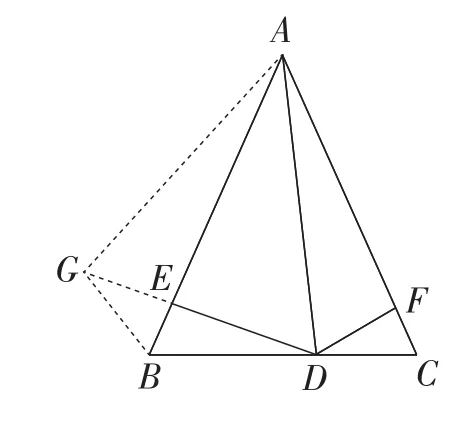
图8

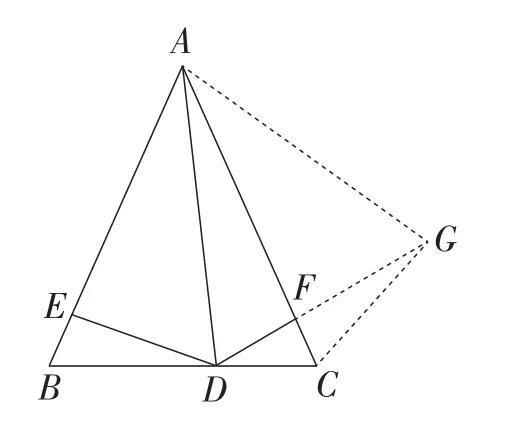
图9

思考3：如图9，如果将△ABD绕点A旋转至△ACG，使AB和AC重合，同理可证.

（2）从相等线段想到圆中等对等定理.

（方法7）如图10，因为∠B+∠C+∠BAC=180°，∠ADE=∠B，∠ADF=∠C，

所以∠EDF+∠EAF=180°.

所以A，E，D，F四点共圆.

因为∠B=∠C，

所以∠ADE=∠ADF.

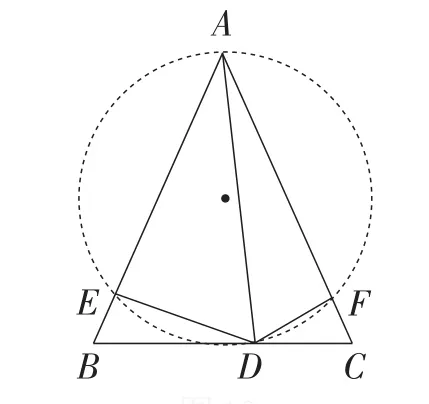
图10

所以AE=AF.

所以BE=CF.

总结：比较上述证法，发现利用三角形相似证明是最基本的方法.

三、变式探究

通过题目条件变化、等价变化、逆向探索，获得题目广泛应用，发展空间观念和创新能力.

探究1：如果将题目中的△ABC改为等边三角形，其余条件不变，结论还成立吗？答案是肯定的.

变式1：如图11，点D是等边三角形ABC的边BC上的一点，点E，F分别在AB，AC边上，且∠ADE=∠ADF=60°.求证：BE=CF.

由于等边三角形是等腰三角形的特殊情形，你能用上述方法完成证明吗？

探究2：条件和结论的互逆变换.

变式2：如图12，点D是△ABC边BC上一点，点E，F分别在AB，AC边上，使BE=CF，且∠ADE=∠B，∠ADF=∠C.求证：AB=AC.

提示：变式2与题目联系密切，你能运用上述证法证明吗？经过分析，思路1（1）、思路1（2）和思路2（2）均能完成变式2的证明.

探究3：等价问题.

如果点D在BC边延长线上，类似作图，上述结论是否成立.若成立，给予证明；若不成立，说明理由.答案是成立的.A

变式3：如图13，D是等腰三角形ABC底边BC延长线上一点，点E，F分别在AB，AC延长线上，且∠ADE=∠ABC，∠ADF+∠ACB=180°.求证：BE=CF.

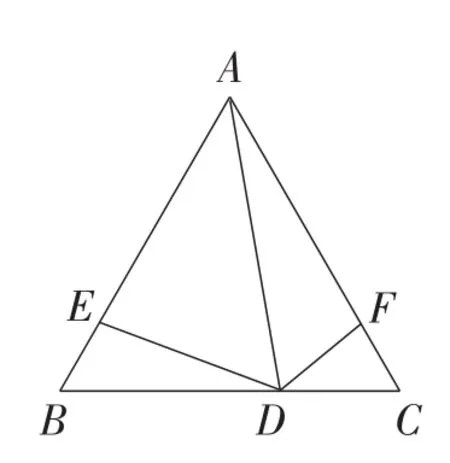
图11

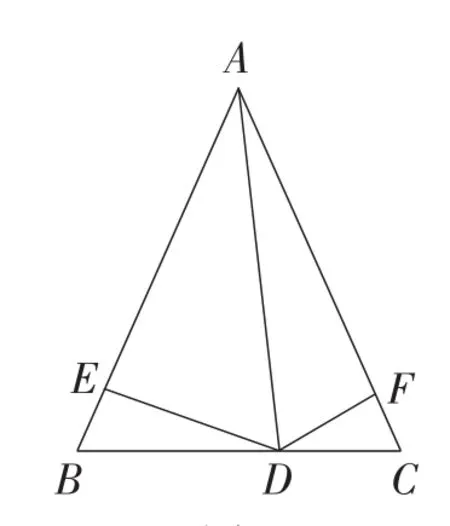
图12

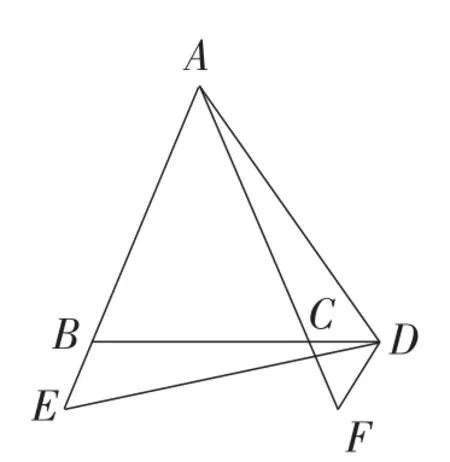
图13

证明：（方法1：利用一线三等角模型）如图13，由于∠ACB=∠ADC+∠CAD，∠ABC=∠ADE=∠ADC+∠BDE，

又因为∠ABC=∠ACB，

所以∠BDE=∠CAD.

因为∠EBD=180°-∠ABC，∠ADF=180°-∠ACB，

所以∠EBD=∠ADF.

所以△BDE∽△CAD.

同理，△CDF∽△BAD.

由①②，推得BE=CF.

（方法2：利用三角形相似）如图13，由于∠ADE=∠ABC，

又因为∠DAE=∠BAD，

所以△ADE∽△ABD.

因为∠ACD=180°-∠ACB，∠ADF=180°-∠ACB，

所以∠ACD=∠ADF.

又因为∠CAD=∠DAF，

所以△ADF∽△ACD.

所以AD2=AF·AC.

因为AB=AC，

所以AE=AF.

则BE=CF.

（方法3：利用四点共圆）如图14，由∠ACB=∠ADC+∠CAD，∠ADE=∠ADC+∠BDE，

且∠ADE=∠ABC，∠ABC=∠ACB，

所以∠BDE=∠CAD.

又∠EBD=180°-∠ABC，∠ADF=180°-∠ACB，

所以∠EBD=∠ADF.

所以△BDE∽△DAF.

所以∠AED=∠AFD.

所以A，E，D，F四点共圆.

所以∠ADE=∠AFE.

又由∠ADE=∠ACB，

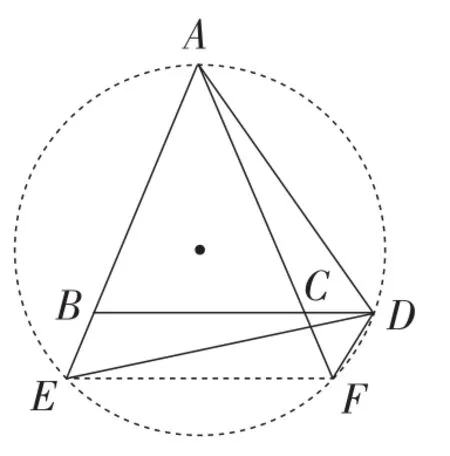
图14

推得∠AFE=∠ACB.

所以BC∥EF.

所以∠AEF=∠ABC.

所以AE=AF.

所以BE=CF.

四、拓展探究

探究1：改变图形.

拓展1：如图15，点P是等腰梯形ABCD底边BC上一点，点E，F分别在边AB，CD上，且∠APF=∠B，∠DPE=∠C.求证：BE=CF.

证明：利用一线三等角模型.

因为∠APC=∠B+∠BAP，∠APC=∠APF+∠CPF，

且∠APF=∠B，

所以∠BAP=∠CPF.

所以△ABP∽△PCF.

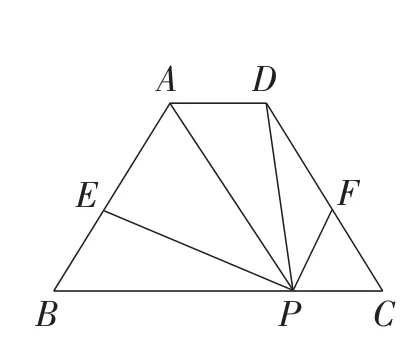
图15

因为AB=CD，

所以BE=CF.

拓展2：如图16，点P是矩形ABCD边BC上一点，点E，F分别在边AB，CD上，且∠APF=∠DPE=90°.求证：BE=CF.

拓展3：如图17，点P是正五边形ABCDE边BC上一点，点F，G分别在AB，CD边上，且∠APG=∠DPF=108°.求证：BF=CG.

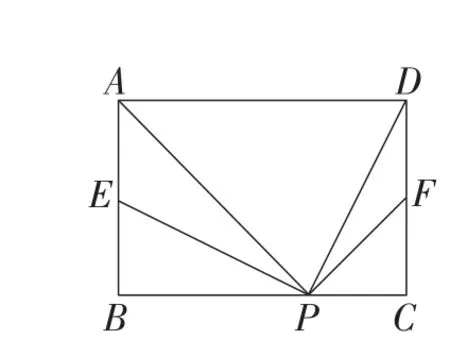
图16

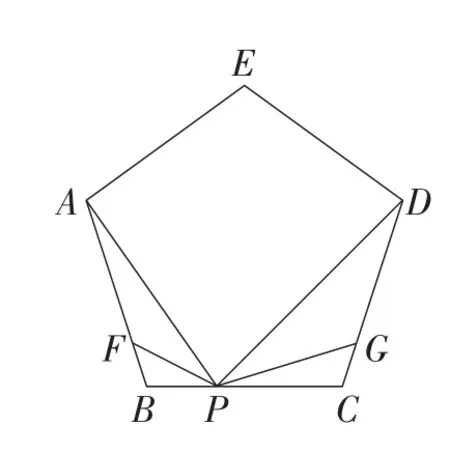
图17

拓展2和拓展3的证明方法也是利用一线三等角模型.

探究2：改变结论.

拓展4：如图18，点P是等腰梯形ABCD底边BC上一点，点E，F分别在BA，DC延长线上，且∠APF=∠B，∠DPE=∠C，PE，PF依次交AD于点G，H.求证：EF∥BC.

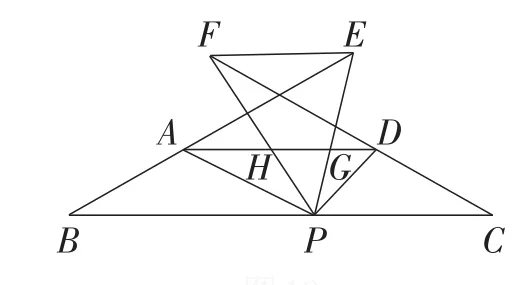
图18

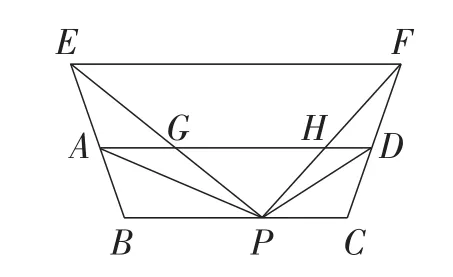
图19

拓展5：如图19，点P是等腰梯形ABCD底边BC上一点，点E，F分别在BA，DC延长线上，且∠APF=∠B，∠DPE=∠C，PE，PF依次交AD于点G，H.求证：四边形EBCF为等腰梯形.

【点拨】拓展4和拓展5关键是证明BE=CF，并通过推得GH∥EF.你能完成证明吗？

探究3：一般化处理.

拓展6：如图20，点D是△ABC边BC上一点，点E，F分别在边AB，AC上，且∠ADE=∠C，∠ADF=∠B.结论BE=CF还成立吗？若成立，给予证明；若不成立，确定BE与CF的大小关系.

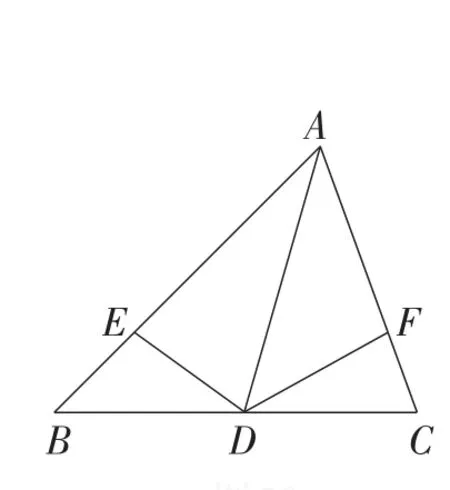
图20

证明：不成立.探索过程如下：利用一线三等角模型.

因为∠ADC=∠B+∠BAD，∠ADC=∠ADF+∠CDF，

又∠ADF=∠B，

所以∠BAD=∠CDF.

又∠ADE=∠C，

所以△ADE∽△DCF.

即AE·CF=DE·DF.

即AF·BE=DE·DF.

由已知推得∠BAC+∠EDF=180°.

所以A，E，D，F四点共圆.

如图21，连接EF，所以∠AEF=∠ADF.

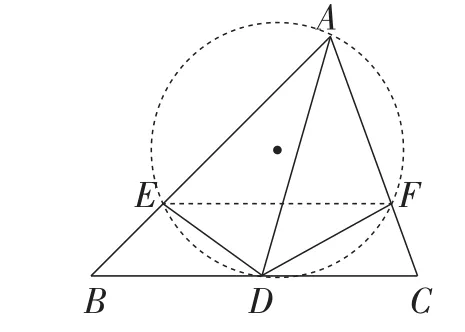
图21

推得∠AEF=∠B.

所以EF∥BC.

可见，当△ABC为等腰（含等边）三角形（AB=AC）时是拓展6的特例.

五、反思

数学教育家波利亚说过，一个有责任心的教师与其穷于应付烦琐的教学内容和过量的题目，还不如适当选择某些有意义但又不太复杂的题目，去帮助学生发掘题目的各个方面，在指导学生解题的过程中，提高他们的才智与推理能力.通过一题多解，变式、拓展探究，对相关习题进行分析，总结解题规律，提高教师解题、命题能力，提高对学生的指导能力.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版，2012.

［3］胡国生，张琥.高考数学试题研究的几种视角［J］.中学数学月刊（高中版），2013（12）:31-33，60.

［4］罗勇，范业润.2016年中考“图形的变化”专题解题评析［J］.中国数学教育（初中版），2017（1/2）：105-115.

［5］白雪峰.挖掘试题育人功能提升学生思维品质：以一道平面几何试题及其变式的解法探究为例［J］.中国数学教育（初中版），2017（7/8）：99-102.

2017─09─09

李发勇（1964—），男，中学高级教师，主要从事初中数学教学、教材及命题研究.