多面体体积计算中的多种思维方法

江苏省沭阳高级中学 陈淮阳

多面体体积计算中的多种思维方法

江苏省沭阳高级中学 陈淮阳

编者的话:“经典题突破方法”栏目里例、习题选名校模拟题或三年高考真题,推出本栏目的主要目的是让同学们更好地领悟数学解题思想方法,通过多解多变培养同学们多思多想的好习惯。学会解题反思,无疑是同学们学习的一条捷径,愿同学们不断在反思中进步,在反思中收获!

对于空间几何体的体积问题,依据题设的特殊性可以用公式法、割补法、等积变换法、分割法、补形法等求解,凸显“非规则体化为规则体”的整体思维的具体应用。本文探究几何体体积计算中的多种思维方法。

一、公式法求体积时的多种思维方法

图1

例1 如图1,在三棱柱A1B1C1-A B C中,D,E,F分别是A B,A C,A A1的中点。设三棱锥F-A D E的体积为V1,三棱柱A1B1C1-A B C的体积为V2,则V1∶V2=。

解法1:注意三棱锥和三棱柱它们的底面和高之间的关系,可用公式法求体积比。设三棱锥F-A D E的高为h,则

解法2:构造辅助的三棱锥。连接A1C,AB,则V=V,而VV,所11A1-ABCA1-ABC2以V=V。12

解法3:特殊化处理。若三棱柱A1B1C1-A B C为正三棱柱,设A B=2,A A1=2,则V2=S h=×22×2=2,V1××1=,所以V∶V=1∶2 4。12

感悟:柱、锥、台的体积计算,确定底面面积和高,用公式V=S h或V=S h或柱体锥体V=(S+S S′+S′)h求解,关键是合台体理选择底面,寻求顶点在底面上的射影。对于体积比的问题,合理设元,沟通关系,分割成常见的规则体,利用加减法得到锥体与非规则体的体积比。

二、三棱锥体积求解中的“公式法”和“直截面分割法”

例2 已知三棱锥S-A B C的所有顶点都在球O的球面上,S C是球O的直径。若平面S C A⊥平面S C B,S A=A C,S B=B C,三棱锥S-A B C的体积为9,则球O的表面积为____。

解法1:取S C的中点O,连接O A,O B,因为S A=A C,S B=B C,所以O A⊥S C,O B⊥S C。因为平面S A C⊥平面S B C,所以O A⊥平面S B C。设O A=r,S C是球O的直径,S A=A C,S B=B C,则 R t△S B C,R t△S A C是等腰直角三角形,且斜边为2r,高为r,所以=×S×O A=×△SBC×2r×r×r==9,所以r=3,所以球的表面积为=3 6 π。

解法2:取S C的中点O,连接O A,O B,因为S A=A C,S B=B C,所以O A⊥S C,O B⊥S C,S C⊥平面O A B。因为平面S A C⊥平面S B C,所以O A⊥平面S B C,而S C是球O的直径,则R t△S B C,R t△S A C是等腰直角三角形。设O A=r,则O B=r,且△A O B为等腰直角三角形,于是有VA-SBC=×S×S C=××r×r×2r=r3△AOB=9,所以r=3,则球的表面积为4 πr2=3 6 π。

感悟:对于三棱锥的体积问题,可以任选一面作底面,然后求出该底面对应的高。关于棱对称的特殊三棱锥,通过作此棱的直截面,将三棱锥分割成共底面的两个三棱锥,该侧棱就是两个小三棱锥高的和。

三、三棱锥体积计算中的“等积变换法”和“分割法”

例3 如图2所示,三棱锥A-B C D中,A B⊥平面B C D,C D⊥B D。

(1)求证:C D⊥平面A B D;

(2)若A B=B D=C D=1,M为A D的中点,求三棱锥AMB C的体积。

解析:(1)因为A B⊥平面B C D,C D⊂平面B C D,所以A B⊥C D。又因为C D⊥B D,A B∩B D=B,A B⊂平面A B D,B D⊂平面A B D,所以C D⊥平面A B D。

图2

(2)解法1:(等积变换法)由A B⊥平面B C D,得A B⊥B D。因为A B=B D=1,所以S=×1×1=。因为M是A D的△ABD中点,所以S=S=×=。△BDM△ABD由(1)知,C D⊥平面A B D,所以三棱锥C-A BM的高h=C D=1,因此三棱锥AMB C的体积V=V=×C D×A-MBCC-DBMS=·1·=。△BDM1解法2:(体积分割法)由A B⊥平面B C D,得平面A B D⊥平面B C D,且平面A B D∩平面B C D=B D。

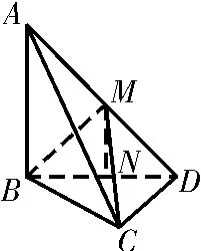
图3

如图3所示,过点M 作MN⊥B D于点N,则MN⊥平面B C D,且MN=A B=。又C D⊥B D,B D=C D=1,所以S=,所以三棱锥A-MB C△CBD的体积VA-MBC=VA-BCD-VM-BCD=(A B-MN)·S=××=。△BCD

感悟:求三棱锥的体积,等积变换是常用的方法,转换原则是换底使高易求或底面放在已知几何体的某一面上;求不规则几何体的体积,常用分割或补形的方法,将不规则几何体转化为规则几何体求解。

四、三棱锥体积计算中的“等积变换法”和“特殊化”

例4 如图4,已知正方体A B C DA1B1C1D1的棱长为1,E,F分别为线段A A1,B1C上的点,则三棱锥D1-E D F的体积为____。

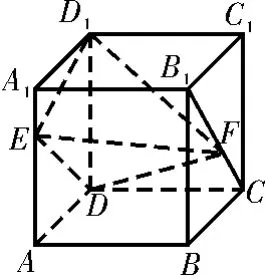
图4

解法1:(等积变换法)三棱锥D1-E D F的体积即为三棱锥F-DD1E的体积。因为E,F分别为A A1,B1C上的点,所以在正方体A B C DA1B1C1D1中,△E DD1的面积为定值,F到平面A ADD的距离为定11值1,所以V=××1=。F-DD1E

解法2:(特殊化)E点移到A点,F点移到C点,则V=V=××1×1D1-EDFD1-ADC×1=。

感悟:把握正方体的特征,合理选择底面使高易求,解法1中注意到△E DD1的面积为定值,F到面E DD1的距离为1,从而使问题简单化;解法2中利用点的特殊性对点进行移动,转化为对特殊四面体的体积求解,凸显等价转化思想的具体应用。

五、正四面体体积计算中的“公式法”和“割补法”

例5 底面边长为2的正三棱锥P-A B C,其表面展开图是△P1P2P3,如图5,求△P1P2P3的各边长及此三棱锥的体积V。

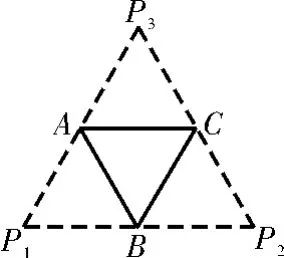
图5

解析:在△P1P2P3中,P1A=P3A,P2C=P3C,所以A C是中位线,故P1P2=2A C=4。同理,P2P3=4,P3P1=4。所以△P1P2P3是等边三角形,各边长均为4,则三棱锥P-A B C是边长为2的正四面体。

解法1:(公式法)如图6,设顶点P在底面A B C内的投影为O,连接B O,并延长交A C于点D,所以D为A C的中点,O为△A B C的重心,P O⊥底面A B C,所以B O=B D=,P O=,V=··2·2··=。解法2:如图7,把正四面体P-A B C补形为正方体A D B EG PHC。设正方体的棱长为a,则有a2+a2=22,解得a=,所以V=()3-4···)2=。

图6

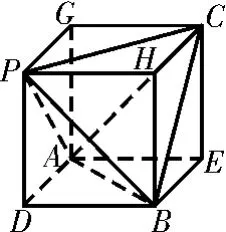
图7

感悟:在棱长为1的正方体中割出一个内接正四面体后,还“余下”4个正三棱锥。每个正三棱锥的体积均为,故内接正四面体的体积为。

六、三棱锥体积计算中的“补形法”

图8

例6 在四面体A B C D中,设A B=1,C D=3,直线A B与C D的距离为2,夹角为,则四面体的体积等于____。

解法1:如图8,将四面体A B C D补成四棱锥A-B D C E,且B E∥C D,B E=C D,则∠A B E=或2,B E=,C D∥面A B E,所以C D与A B的距离,即为C D到平面A B E的距离,即C到平面A B E的距离,也就是三棱锥C-A B E的高h=2,所以VA-BCD=VA-BEC=VC-ABE=S=×2××A B×B E×△ABEs i n=。

解法2:如图9,把四面体A B C D补成三棱柱A B E-F C D,则面A B E∥面C D F,A B∥C F,且C F=1,则A B与C D的距离就是平面A B E与平面F C D的距离,即三棱柱的高h=2,且∠D C F=或。所以V=S·h=×柱△FCDC D×C F×s i n×2=,故四面体的体积V=V=。A-BCD柱

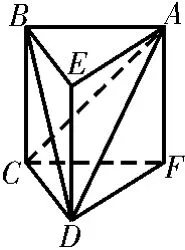
图9

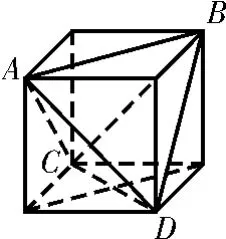
图10

解法3:如图1 0,把四面体A B C D补成平行六面体,则四面体的体积是平行六面体体积的,V平行六面体=·h=×1×3×s i n×2=,故四面体的体积为。

感悟:三棱锥补成四棱锥、三棱柱或正方体可以简化求体积问题,本题将两异面的直线段构成的四面体用三种不同的补形探究出其结论:在四面体A B C D中,设A B=a,C D=b,直线A B与C D的距离为h,夹角为θ,则四面体的体积V=a b hs i nθ。

(责任编辑 王福华)