空间几何解析几核心考点B卷

河南省商丘市第一高级中学 张志华

空间几何解析几核心考点B卷

河南省商丘市第一高级中学 张志华

编者的话:强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能把试卷保存好,对以后的复习大有裨益。

一、选择题

1.若抛物线y2=2p x的焦点与椭圆+=1的右焦点重合,则p的值为( )。

A.-2 B.2 C.-4 D.4

2.设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )。

A.若l⊥α,α⊥β,则l⊂β

B.若l∥α,α∥β,则l⊂β

C.若l⊥α,α∥β,则l⊥β

D.若l∥α,α⊥β,则l⊥β

3.方程2x2-5x+2=0的两个根可分别作为( )。

A.一椭圆和一双曲线的离心率

B.两抛物线的离心率

C.一椭圆和一抛物线的离心率

D.两椭圆的离心率

图1

4.如图1,A1B1C1-A B C是直三棱柱,∠B C A=9 0°,点 D1,F1分别是A1B1,A1C1的中点,若B C=C A=C C1,则B D1与A F1所成角的余弦值是( )。

5.已知向量a=(1 ,1,0),b=(- 1,0,2),且k a+b与2a-b互相垂直,则k的值为( )。

7.直三棱柱A B C-A1B1C1的底面A B C为等腰直角三角形,斜边A B=2,侧棱A A1=1,则该三棱柱的外接球的表面积为( )。

A.2 π B.3 π C.4 π D.5 π

9.动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,那么点P的轨迹方程为( )。

A.x2+y2=3 2 B.x2+y2=1 6

C.(x-1)2+y2=1 6

D.x2+(y-1)2=1 6

1 0.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )。

1 1.在正三棱锥S-A B C中,M,N分别是棱S C,B C的中点,且MN⊥AM,若侧棱S A=2 3,则正三棱锥S-A B C的外接球的表面积是( )。

A.1 2 π B.3 2 π C.3 6 π D.4 8 π

1 2.设斜率为2的直线l过抛物线y2=a x(a≠0)的焦点F,且和y轴交于点A,若△O A F(O为坐标原点)的面积为4,则抛物线方程为( )。

A.y2=±4x B.y2=±8x

C.y2=4x D.y2=8x

1 3.过椭圆+=1(a＞b＞0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1P F2=6 0°,则椭圆的离心率为( )。

1 4.已知P为椭圆+=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为( )。

1 5.椭圆+=1的一条弦被A(4,2)平分,那么这条弦所在的直线方程是( )。

A.x-2y=0B.2x+y-1 0=0

C.2x-y-2=0 D.x+2y-8=0

1 6.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )。

A.若m∥α,n∥α,则m∥n

B.若α⊥γ,β⊥γ,则α∥β

C.若m∥α,m∥β,则α∥β

D.若m⊥α,n⊥α,则m∥n

1 7.过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( )。

A.一条 B.两条 C.三条 D.四条

1 8.棱长为1的正方体A C1中,E,F分别为A A1和A B的中点,则点E到直线C F的距离为( )。

C.直线不经过第二象限

D.当t=1时,直线上对应点到点(1,2)的距离为3 2

2 0.若☉C:x2+y2-4x-2y-5=0与x轴正半轴交于点A,则☉C在A处的切线方程为( )。

A.3x-y+1 5=0 B.3x-y-1 5=0

C.3x+y-1 5=0 D.3x+y+1 5=0

A.(1,+∞) B.(0,1)

C.(1,2) D.与k有关

2 2.二面角α-l-β是直二面角,A∈α,B∈β,设直线A B与α、β所成的角分别为∠1和∠2,则( )。

A.∠1+∠2=9 0° B.∠1+∠2≥9 0°

C.∠1+∠2≤9 0° D.∠1+∠2＜9 0°

2 3α.、β是两个不重合的平面,在下列条件下,可判定α∥β的是( )。

Aα.、β都平行于直线l、m

Bα.内有三个不共线的点都到β的距离相等

Cl.、m是α内的两条直线且l∥β,m∥β

Dl.、m是两条异面直线且l∥α,m∥α,l∥β,m∥β

2 4.在正四面体P-A B C中,D、E、F分别是A B、B C、C A的中点,下面四个结论中不成立的是( )。

A.B C∥平面P D F

B.D F⊥平面P A E

C.平面P D F⊥平面A B C

D.平面P A E⊥平面A B C

A.R B.[-4,4]

C.[-3,3] D.[-2,2]

2 6.如图2,已知球O是棱长为1的正方体A B C DA1B1C1D1的内切球,则平面A C D1截球O的截面面积为( )。

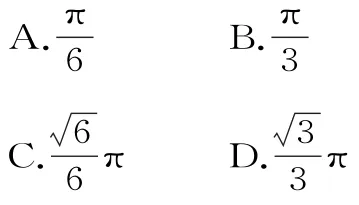
图2

2 7.已知双曲线-=1(a＞0,b＞0)的右焦点为F,若过点F且倾斜角为6 0°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )。

A.(1,2)B.(1,2]

C.[2,+∞) D.(2,+∞)

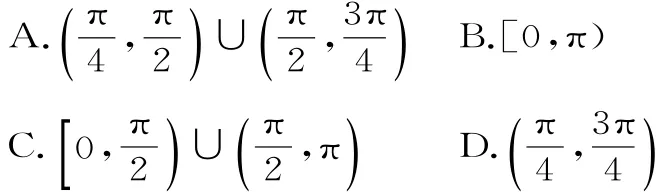
二、填空题

2 9.双曲线4x2-y2=1的离心率为。

3 0.设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点,若A B的中点为(2,2),则直线l的方程为____。

3 1.将一张坐标纸折叠一次,使得点(0,2)与点(-2,0)重合,且点(20 1 7,20 1 8)与点(m,n)重合,那么n-m=。

3 2.三棱锥D-A B C的三个侧面分别与底面全等,且A B=A C=3,B C=2,则二面角A-B C-D的大小为____。

3 4.已知△A′B′C′是正△A B C水平放置图形的直观图(A′为原点),若△A B C的边长为2,则C′A′2-C′B′2=。

3 5.已知△A B C的周长为1 6,B C=6,则S△ABC的最大值为____。

3 6.已知过点A(-4,m)和B(m,6)的直线与直线4x-2y+1=0垂直,则m的值为。

3 8.直线y=2x+m和圆x2+y2=1交于点A、B,以x轴的正方向为始边,O A为终边(O是坐标原点)的角为α,O B为终边的角为β,那么s i n(α+β)=。

3 9.某种乳饮料的外包装是一个四面体,这个四面体的每个面都是腰长为1 0c m,底边长为6c m的等腰三角形,则该四面体的容积为c m3(外包装的厚度与接缝忽略不计)。

4 0.直三棱柱A B C-A1B1C1中,∠A C B=9 0°,C A=C B=1,C=2,D为C C1的中点,E、F分别为与A B上的动点,若D E⊥D F,则E F的最小值为____。

其中为真命题的是____。(写出所有真命题的序号)

三、解答题

4 2.已知圆(x-2)2+y2=1,求:

(1)x2+y2的最大值;

4 3.如图3,在底面是菱形的四棱锥S-A B C D 中,∠A B C=6 0°,S A=A B=a,S B=S D=S A,点P在S D上,且S D=3P D。

(1)证明S A⊥平面A B C D;

(2)设E是S C的中点,求证B E∥平面A P C。

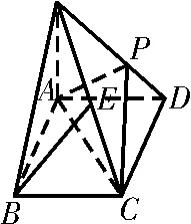
图3

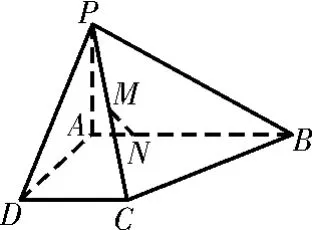
图4

4 4.如图4所示,在四棱锥P-A B C D中,A B⊥A D,A D⊥D C,P A⊥底面A B C D,P A=A D=D C=A B=1,M为P C的中点,点N在A B上且AN=NB。

(1)证明:MN∥平面P A DN;

(2)求直线MN与平面P C B所成的角。

4 5.已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为,两个焦点分别为F1和F2,椭圆G上一点到F1和F2的距离之和为1 2。圆Ck:x2+y2+2k x-4y-2 1=0(k∈R)的圆心为点Ak。

(1)求椭圆G的方程。

(2)求△AkF1F2的面积。

(3)问:是否存在圆Ck包围椭圆G?请说明理由。

图5

4 6.如图5,在直四棱柱A B C D-A1B1C1D1中,底面A B C D为直角梯形,∠B A D=∠A D C=9 0°,A B=A D=1,C D=C C1=2,E为棱A A1的中点,G为棱C1D1的中点,F为棱B B1上一动点。

(1)求证:E G∥平面F C C1;

(2)求三棱锥E-F C C1的体积。

(1)求椭圆C与直线l的方程;

(2)求△O A B的面积(O为坐标原点)。

4 8.图6所示的多面体是直平行六面体A B C D-A1B1C1D1经平面A E F G所截后得到的图形,其 中 ∠B A E= ∠G A D=4 5°,A B=2A D=2,∠B A D=6 0°。

图6

(1)求证:B D⊥平面A D G;

(2)求平面A E F G与平面A B C D所成锐二面角的余弦值;

(3)求点C到平面A E F G的距离。

4 9.在长方体A B C DA1B1C1D1中,A B=B C=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图7所示的几何体A B C D-A1C1D1,且这个几何体的体积为。

图7

(1)证明:直线A1B∥平面C DD1C1;

(2)求棱A1A的长;

(3)求经过A1,C1,B,D四点的球的表面积。

图8

5 0.如图8,已知直线l:y=k x-2与抛物线C:x2=-2p y(p＞0)交于A,B两点,O为坐标 原 点,+=(-4,-1 2)。

(Ⅰ)求直线l和抛物线C的方程;

(Ⅱ)抛物线上一动点P从A到B运动时,求△A B P面积的最大值。

(1)求椭圆的方程;

(2)设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(-a,0),点(0,y)在线段A B的垂直平分线上,且 ·4,求y0的值。

(责任编辑 刘钟华)