微薄膜多场耦合非线性振动分析

付晓瑞， 党亚辉， 许立忠

(燕山大学 机械工程学院，河北 秦皇岛 066004)

微薄膜多场耦合非线性振动分析

付晓瑞， 党亚辉， 许立忠

(燕山大学 机械工程学院，河北 秦皇岛 066004)

将微谐振压力传感器谐振薄膜简化为微薄膜多场耦合系统，给出考虑分子力作用时微薄膜多场耦合动力学方程，利用Linz Ted-Poincaré方法求得其非线性振动固有频率与振型方程，研究了分子力对薄膜非线性固有频率及自由振动的影响规律，利用微加工技术制作出谐振薄膜，利用静电激励-电容检测方法对薄膜非线性固有频率进行了测试。结果表明：当薄膜尺寸较小时，分子力对于微薄膜多场耦合非线性振动的固有频率具有较大影响。研究结果对于压力传感器进一步微型化具有指导意义。

分子力；多场耦合；非线性振动；MEMS

微机电系统(MEMS)具有结构紧凑、成本低、功耗小、响应速度快以及精度高等优点[1-2]。硅微谐振传感器因其输出频率信号，不会发生失真，适合长距离传输，受到人们关注[3]。其中，对硅微谐振压力传感器中谐振器振动研究的关注尤为显著[4]。微谐振压力传感器的谐振结构多为微梁式和微薄膜式两种，其中薄膜式微谐振压力传感器输出的测试信号较强，对测试电路的要求较低，更符合传感器集成化、微型化的发展方向[5-6]。

Alonso等[7]对NiCr薄膜微谐振式压力传感器谐振子的振动特性进行了研究。Fan等[8]对微谐振式压力传感器的非线性振动进行了研究，利用多尺度法求解出非线性项对传感器固有频率的影响规律。张建等[9]对MEMS中薄膜结构在范德华力作用下的粘附问题进行了研究。张俊生等[10]求解出薄膜式微谐振压力传感器中薄膜的二维振动方程。乔磊等[11]对薄膜结构动力全过程进行了分析。Liu等[12]对薄膜非线性自由振动以及在冲击载荷下的受迫振动进行了理论分析。唐黎明等[13]研究了范德华力对微悬臂梁动力模型及分岔的影响，结果表明范德华力在微纳尺度下的影响不可忽略。张艳敏等[14]利用微机械加工技术设计制造出矩形薄膜压力传感器芯片。

随着系统尺寸、间隙进一步减小到微米、纳米量级，微构件间的分子力对谐振子非线性振动特性的影响变得越来越明显。而谐振薄膜的振动特性直接影响到薄膜压力传感器的工作性能[15-16]。当谐振薄膜在微尺度效应下，机械场、电场以及分子力等多场相互作用，对薄膜非线性振动均有影响，且电场力和分子力对振动频率影响较大，而振动频率对于谐振式压力传感器至关重要，若仅仅分析单一场，则存在一定的局限性，因此对于微纳米级别的谐振薄膜进行多场耦合振动研究具有重要意义。基于上述原因，本文建立了微薄膜多场耦合振动模型，对薄膜系统非线性振动进行研究分析，得到谐振薄膜多场耦合非线性振动固有频率和位移响应表达式，对考虑范德华力时对非线性频率及时域响应影响进行了研究，通过实验验证了本文理论分析的正确性。

1 动力学方程

图1所示为静电激励微薄膜物理模型，下层为固定的压力感受膜，上层为可变形的运动薄膜。当对两者施加静电激励时，两者之间形成电场力，振动薄膜相对固定薄膜发生相对位移，形成振动，同时在薄膜上存在着范德华力。因此，该模型为静电场力，范德华力和弹性恢复力作用下的微薄膜多场耦合系统。图中u(x,y,t)表示任意时刻振动薄膜与固定极板之间的距离，w(x,y,t)表示薄膜沿z轴方向的振动位移。v为两极板间的初始距离，则

u(x,y,t)=v-w(x,y,t)

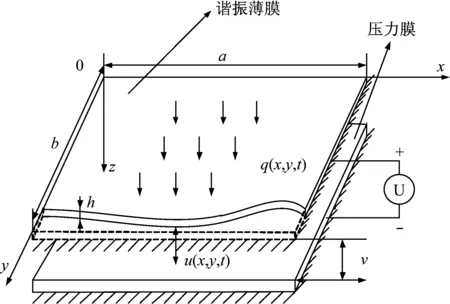
图1 微薄膜多场耦合结构模型Fig.1 Multi-field coupled structural model of micro film

微薄膜动态弯曲振动方程为[17]

(1)

式中，F为单位长度薄膜张力，假设保持常值。

Δq为单位面积薄膜沿z轴的分布力，包括电场力和范德华力，即

Δq=Δq0+Δqr

(2)

其中动态单位面积的范德华力为

式中，A为Hamaker常数，A=10-19J。

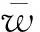
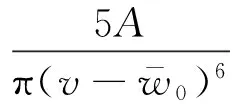
(3)

因薄膜位移变化引起单位面积动态电场力为

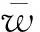
(4)

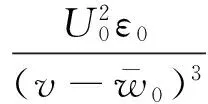
(5)

2 系统非线性自由振动

将式(5)代入振动方程中得

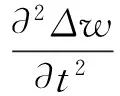
(6)

令Δw=φ(x,y)q(t)代入式(6)得到

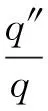
(7)

其中

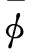
忽略作用力非线性对系统的模态函数产生的影响，则令式(7)左右等于-ω0，设ω0为谐振薄膜系统线性的固有频率，即：

(8)

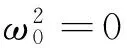
(9)

对于式(9)可以得到

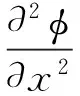
(10)

取满足四边固定边界条件的模态函数为

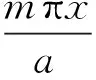
(11)

其中S为常数。

将式(11)代入式(10)可得

(12)

式中

式(12)对薄膜任意一点都成立，则

可以得到四边固定薄膜在多场耦合时的固有频率为

ω0=

(13)

可取满足四边固定边界条件的模态函数为

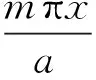
(14)

对于式(8)，可以得到广义时间坐标的动力学方程

(15)

本文利用林滋泰德-庞加莱法求解非线性系统的动力学方程，令

q(t)=q0(t)+εq1(t)+ε2q2(t)+…

(16)

同时，将线性系统的自由频率也展成ε的幂级数

(17)

将式(16)和式(17)代入式(15)中，并令ε的同次幂系数相等，可以得到

(18a)

(18b)

(18c)

设系统的初始广义位移k0，各方程的初始条件为

(19)

由式(18a)可以得到

q0(t)=k0cosφ

(20)

其中

φ=ωt

将式(20)代入一次近似方程，得到

(21)

为了避免久期项，令式(21)中cosφ的系数为零，可得

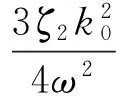
(22)

进而得到

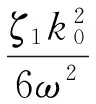
(23)

同理可得

(24)

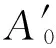
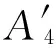
(25)

式中

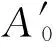
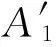
将式(20)、式(23)以及式(25)代入式(16)中，可以得到

(26)

式中

将式(22)、式(24)代入式(17)中，可以得到非线性系统自由振动幅频相应关系为

(27)

3 实例计算与分析

3.1 频率特性

本文采用的微薄膜参数如表1所示，初始激励幅值k0=2×10-7m，将表1所示参数代入式(13)和式(27)中，表2为微薄膜多场耦合系统非线性振动固有频率随激励电压的变化规律(其中v=0.50 μm)，表3为微薄膜多场耦合系统非线性振动固有频率随薄膜初始间隙的变化规律(其中U0=0.2v)，其中ω1为不考虑分子力时非线性振动频率，ω2为考虑分子力时非线性振动频率，η为两者的相对偏差。可以得知：

(1)考虑静电场力和范德华力作用的薄膜各阶固有频率均小于只考虑静电场力作用的固有频率，这是因为范德华力对于薄膜振动相当于一个软弹簧系统，因此范德华力能够引起薄膜固有频率的降低。

(2)随着阶数的增加，考虑范德华力的薄膜机电耦合非线性振动固有频率与不考虑范德华力的薄膜机电耦合非线性振动固有频率差异减小，如对于v=0.45 μm，mode(1,1)固有频率相对偏差为7.95%，而对于mode(4,4)固有频率相对偏差为0.27%。

表1 系统计算参数Tab.1 System Parameters

表2 非线性频率随激励电压的变化规律Tab.2 Changes of nonlinear frequencies with voltages

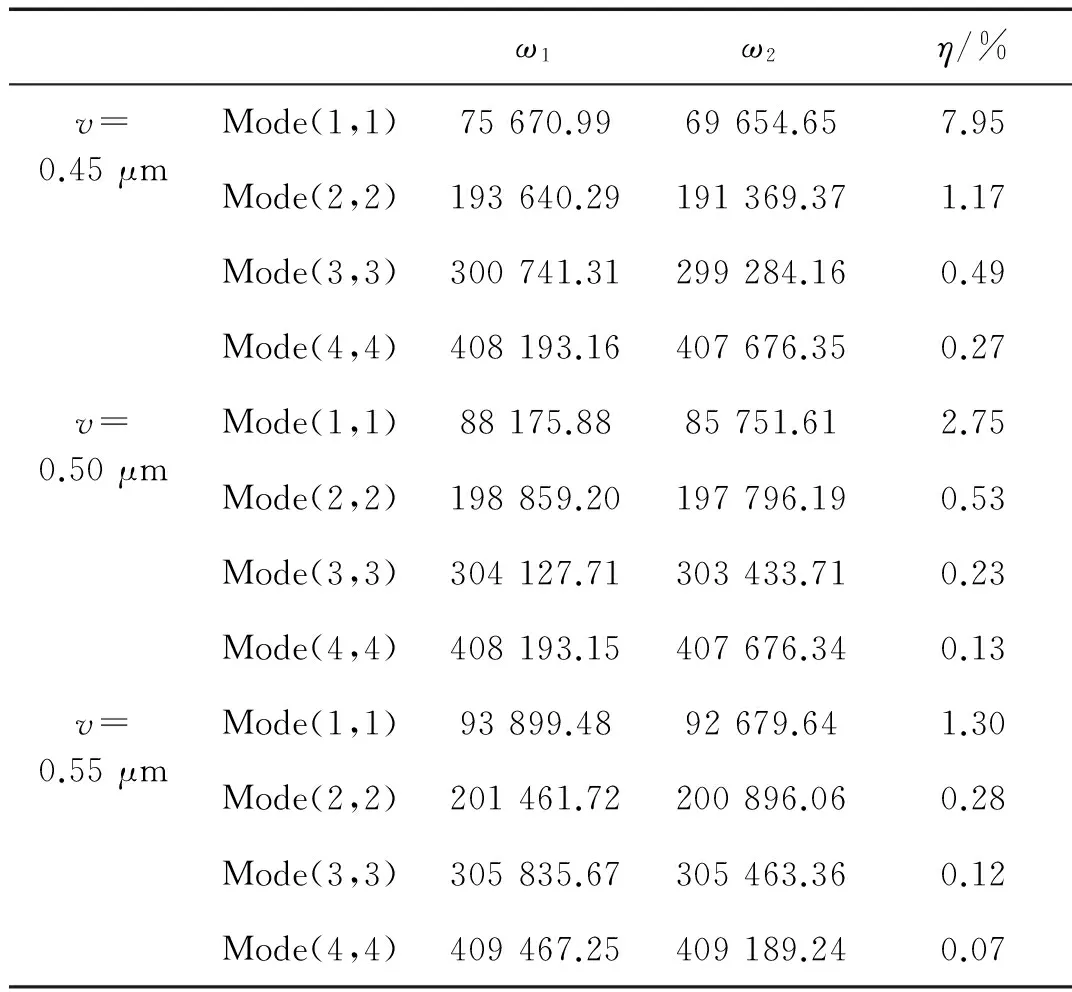
表3 非线性频率随初始间隙的变化规律Tab.3 Changes of nonlinear frequencies with initial clearance

(3)当工作电压增加时，考虑范德华力与不考虑范德华力薄膜固有频率相对偏差增大，如对于U0=0.2v，mode(1,1)固有频率相对偏差为2.75%，对于U0=0.35v，mode(1,1)固有频率相对偏差为11.35%。这是因为工作电压减小时，谐振薄膜与固定基板之间的电场强度降低，导致薄膜弹性变形减小，从而间隙增大，分子力影响程度降低。

(4)当谐振薄膜与固定基板之间的初始间隙增大时，考虑范德华力与不考虑范德华力时薄膜固有频率相对偏差减小，如对于v=0.45 μm，mode(1,1)固有频率相对偏差为7.95%，v=0.55 μm，mode(1,1)固有频率相对偏差为1.30%。

3.2 时域分析

为了研究范德华力对薄膜非线性振动时域动态响应的影响，将薄膜中心处考虑范德华力时的动态响应与不考虑范德华力时的动态响应进行求差。图2为动态响应差随薄膜参数变化规律。可以得知：

(1)随着响应时间的增加，响应差先增大后减小，表明范德华力对时域动态响应的影响随时间变化成周期性变化。

(2)当初始间隙变化时响应差变化剧烈，且间隙越小响应差的幅值越大，因此对于初始间隙较小时，范德华力的影响较大，不可忽略。

(a) 初始间隙v

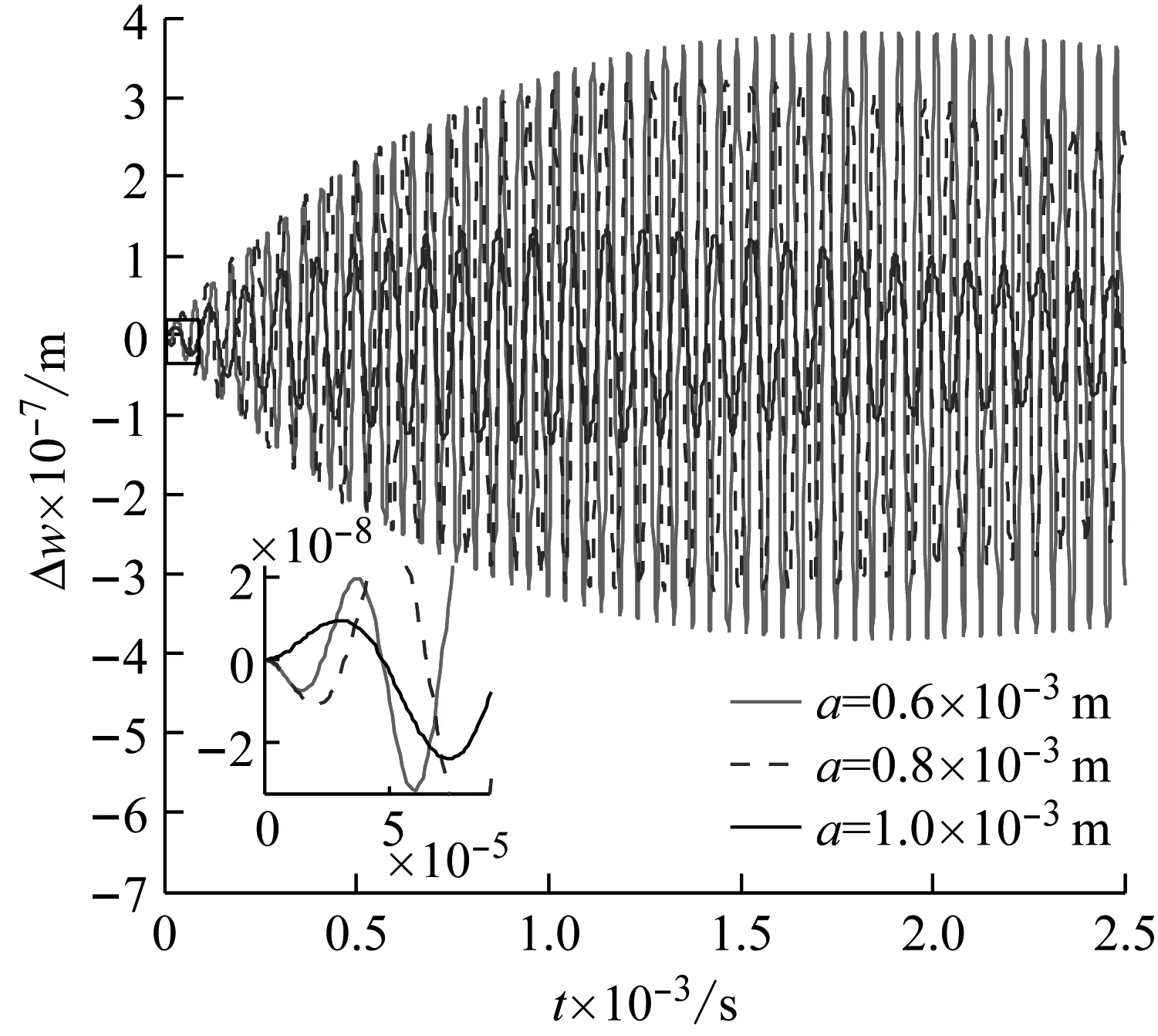
(b) 薄膜长度a图2 响应差随参数变化Fig.2 Difference of the vibrating amplitudes as function of Parameters

(3)随着薄膜长度增大，响应差的幅值增大，但当薄膜长度变化时响应差的幅值变化不大，因此，响应差对于薄膜长度的变化不敏感。

3.3 实验分析

本实验采用静电激励-电容检测的方法进行振动频率的测量，当静电驱动的频率接近薄膜非线性固有频率时，薄膜发生共振，此时位移响应出现极值，从而输出的电压信号也最大，通过观察输出的幅频图中极值点所对应的频率来确定微薄膜的固有频率。实验中使用的谐振薄膜由光刻、腐蚀等工艺制作而成，如图3所示。表4为被测薄膜物理参数，其中薄膜初始间隙为v=0.5 μm和v=1.0 μm两种。图4为实验现场图，主要包括：激励输出部分、传感器振动部分以及振动信号采集部分。其中振动信号采集系统利用自行设计的开环检测系统，如图5所示。

图3 谐振薄膜Fig.3 Resonant film表4 被测薄膜参数Tab.4 Parameters of measured micro-film

长度a/mm宽度b/mm厚度h/μm激励电压U0/v薄膜密度ρ/(kg·m-3)1.120.5160.152330

图4 实验现场图Fig.4 Experimental site map

输出信号中包括一倍频和三倍频两种频率成分，且三倍频与激励电压、激励频率成正比，与谐振薄膜的位移同相位，因此本实验检测的是薄膜振动的三倍频。图6为v=0.5 μm和v=1.0 μm时测试结果中微薄膜幅频图，由图可以得知对于v=0.5 μm，当输入激励频率为8.03 kHz时，其三倍频的输出幅值最大，因此可以得到薄膜非线性固有频率为8.03 kHz。同理，对于v=1.0 μm，薄膜非线性固有频率为8.80 kHz。表5和表6分别为v=0.5 μm和v=1.0 μm时实验结果与理论结果的对比。由表5和表6可知，对于小间隙薄膜：考虑范德华力时理论值为8 133.11Hz，实验值为8 030 Hz，相对偏差为1.28%；不考虑范德华力时理论值为8 349.32 Hz，与实验值的相对偏差为3.98%。对于大间隙薄膜：考虑范德华力理论值为9 072.88 Hz，实验值为8 800 Hz，相对偏差为3.10%；不考虑范德华力时理论值为9 076.76 Hz，与实验值相对偏差为3.14%。从而验证了当初始间隙较小时，范德华力对薄膜式微谐振压力传感器的影响不可忽略。

图5 开环检测系统Fig.5 Open loop detection system

(a) v=0.5 μm

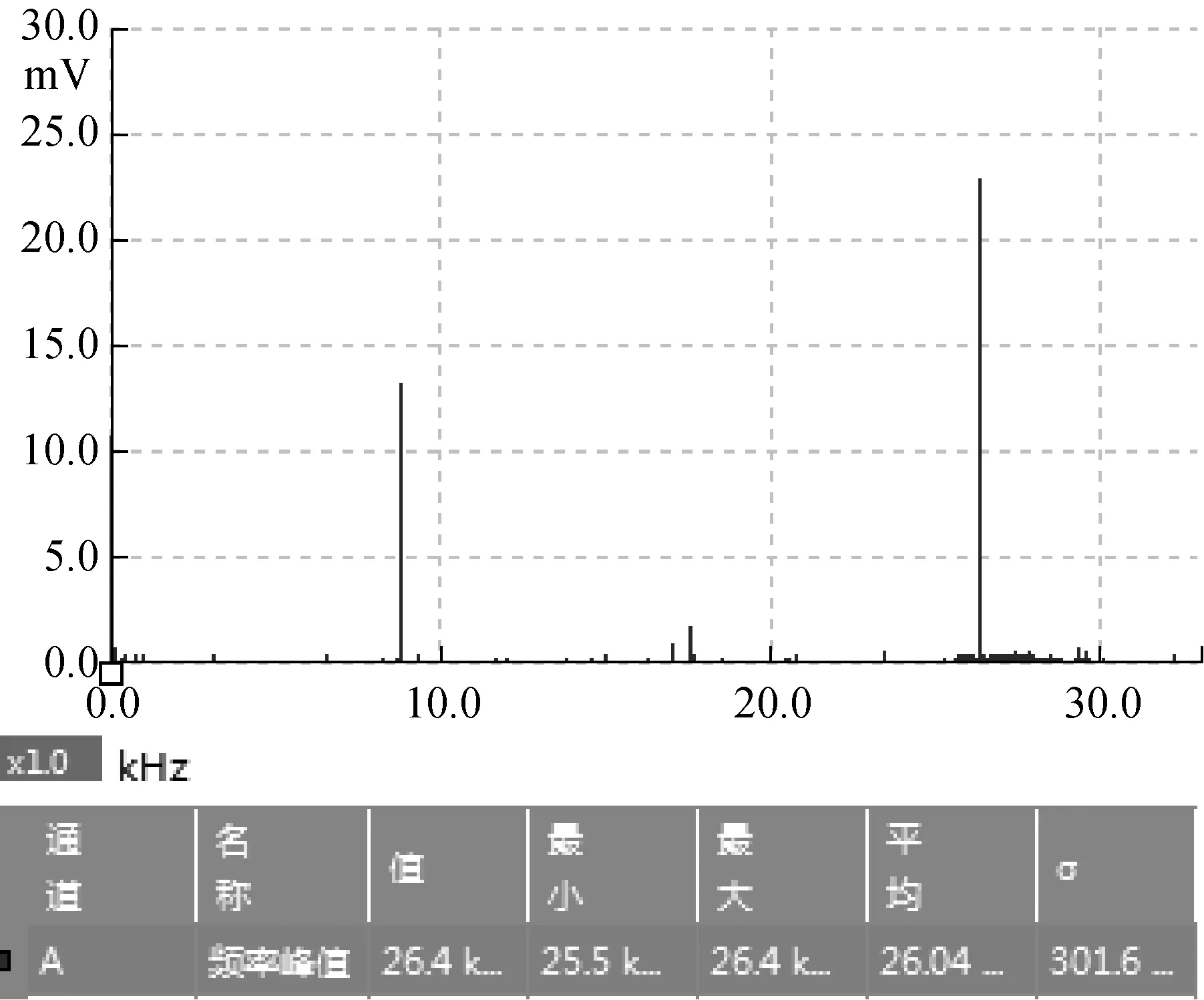
(b) v=1.0 μm图6 微薄膜幅频图Fig.6 Amplitude frequency diagram of micro-film表5 实验结果与理论值比较(v=0.5 μm)Tab.5 Comparison of experimental results andtheoretical values(v=0.5 μm)

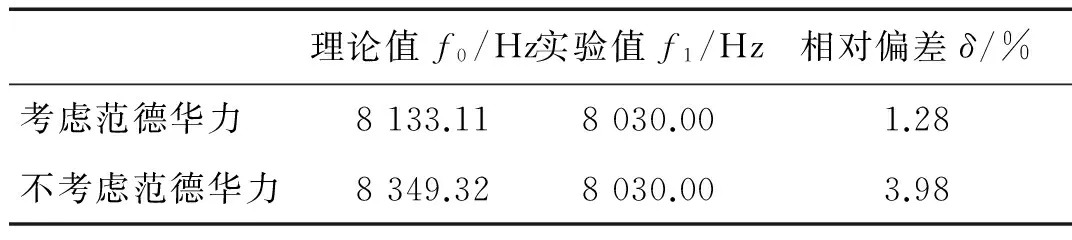
理论值f0/Hz实验值f1/Hz相对偏差δ/%考虑范德华力8133.118030.001.28不考虑范德华力8349.328030.003.98

表6 实验结果与理论值比较(v=1.0 μm)Tab.6 Comparison of experimental results andtheoretical values(v=1.0 μm)

4 结 论

本文建立了考虑范德华力时微薄膜多场耦合非线性振动方程，利用Linz Ted-Poincaré方法求出薄膜非线性固有频率以及位移响应函数。对频率特性以及位移响应进行了分析，利用静电激励-电容检测的方法对薄膜非线性振动固有频率进行测试。结果表明：当激励电压较大，薄膜初始间隙较小时，范德华力对薄膜非线性振动固有频率影响较大；薄膜振动固有频率实验值与理论值非常接近，验证了固有频率理论分析的正确性。研究结果对于传感器进一步微型化具有一定意义。

[1] THIELICKE E, OBERMEIER E. Microactuators and their technologies[J]. Mechatronics, 2000, 10: 431-455.

[2] RAFAEL N G, ANNA M B, ALFONS D. AC transfer function of electrostatic capacitive sensors based on the 1-D equivalent model: application to silicon microphones[J]. Journal of Microelectromechanical Systems,2003,12(6):972-978.

[3] 苑伟政, 任森, 邓进军,等. 硅微机械谐振压力传感器技术发展[J]. 机械工程学报, 2013, 49(20):2-9.

YUAN Weizheng, REN Sen, DENG Jinjun, et al. A review of silicon micromachined resonant pressure sensor[J]. Journal of Mechanical Engineering, 2013, 49(20):2-9.

[4] 张琪昌, 周凡森, 王炜. 压膜阻尼作用下微机械振器动力学分析[J]. 振动与冲击, 2015，34(17):124-130.

ZHANG Qichang, ZHOU Fanseng, WANG Wei. Dynamic characteristics of a micro-mechanical-resonator with squeeze film damping[J]. Journal of Vibration and Shock, 2015, 34(17):124-130.

[5] YUAN W, REN S, DENG J, et al. A review of silicon micromachined resonant pressure sensor[J]. Journal of Mechanical Engineering, 2013, 49(20):2-9.

[6] XU Lizhong, FU Xiaorui. Electromechanical fluidic coupled vibrations for micro film considering the van der Waals force[J]. Journal of Vibroengineering, 2015, 17(1):455-467.

[8] FAN S. Investigation on nonlinear vibration characteristics of resonant silicon microstructure pressure sensor[J]. Chinese Journal of Scientific Instrument, 2006, 27(12):1670-1673.

[9] 张建, 丁建宁, 王权,等. 范德华力对硅基微悬臂梁抗粘附稳定性的影响[J]. 机械强度, 2007, 29(6):923-926.

ZHANG Jian, DING Jianning, WANG Quan, et al. Adhesion stability of silicon microcantilevers under van der waals forces[J]. Journal of Mechanical Strength, 2007, 29(6):923-926.

[10] 张俊生. 薄膜二维振动数理方程的推导与求解[J]. 榆林学院学报, 2006, 16(6):29-31.

ZHANG Junsheng. Inferential reasoning and solution of thin film 2D vibration M & P equation[J]. Journal of Yulin College, 2006, 16(6):29-31.

[11] 乔磊, 谭峰, 杨庆山. 薄膜结构的动力反应分析[J]. 振动与冲击, 2011, 30(6):109-113.

QIAO Lei, TAN Feng, YANG Qingshan. Dynamic analysis of membrane structures[J]. Journal of Vibration and Shock, 2011, 30(6):109-113.

[12] LIU Changjiang, ZHENG Zhoulian, JUN Long, et al. Dynamic analysis for nonlinear vibration of prestressed orthotropic membranes with viscous damping[J]. International Journal of Structural Stability & Dynamics, 2013, 13(13):60-66.

[13] 唐黎明, 谢进, 谢蛟,等. 范德华力对微悬臂梁动力模型及分岔的影响[J]. 机械设计与研究, 2014(3):71-75.

TANG Liming，XIE Jin，XIE Jiao，et al. The impact of vander waals force on the dynamics model and bifurcation for a micro-cantilever[J]. Machine Design and Research, 2014(3):71-75.

[14] 张艳敏, 王权, 李昕欣. 表面微机械加工的高长宽比矩形薄膜压力传感器[J]. 仪表技术与传感器, 2014(2):14-15.

ZHANG Yanmin, WANG Quan, LI Xinxin. Study of surface micro-machined absolute pressure sensor with long and narrow rectangular film[J]. Instrument Technique & Sensor, 2014(2):14-15.

[15] 陈德勇, 曹明威, 王军波,等. 谐振式MEMS压力传感器的制作及圆片级真空封装[J]. 光学精密工程, 2014, 22(5):1235-1242.

CHEN Deyong, CAO Mingwei, WANG Junbo, et al. Fabrication and wafer-level vacuum packaging of MEMS resonant pressure sensor[J]. Optics and Sprecision Engineering, 2014, 22(5):1235-1242.

[16] 李晓莹, 张艳飞, 任森,等. 基于稳态扫频的MEMS谐振压力传感器芯片测试[J]. 微纳电子技术, 2013(4):224-228.

LI Xiaoying, ZHANG Yanfei, REN Sen, et al. MEMS resonant pressure sensor chip testing based on the steady-state sweep[J]. Micronanoelectronic Technology, 2013(4):224-228.

[17] 林文静, 陈树辉, 李森. 圆形薄膜自由振动的理论解[J]. 振动与冲击, 2009, 28(5):84-86.

LIN Wenjing, CHEN Shuhui, LI Sen. Analytical solution of the free vibration of circular membrane[J]. Journal of Vibration and Shock, 2009, 28(5):84-86.

Multi-fieldcouplednonlinearvibrationanalysisofmicro-films

FU Xiaorui， DANG Yahui， XU Lizhong

(School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

Here, dynamic equations of a multi-field coupled micro-film were deduced considering the action of molecular forces. Utilizing Linz Ted-Poincaré method, the micro-film’s nonlinear natural frequencies and corresponding vibrational shape equation were derived. The effects of molecular forces on the micro-film’s nonlinear natural frequencies and free vibration were analyzed. A resonant film was designed and manufactured using the micro-processing technique. The method of electrostatic excitation-capacitance detection was used to measure the micro film’s nonlinear natural frequencies. The results showed that the smaller the size of the micro-film, the larger the effects of molecular forces on the micro-film’s nonlinear natural frequencies. The study results had a guiding significance for the further miniaturization of pressure sensors.

molecular force; multi-field coupled; nonlinear vibration; MEMS

河北省重点基础研究项目(13961701D)；河北省博士研究生创新资助项目(CXZZBS2017043)

2016-06-22 修改稿收到日期：2016-09-16

付晓瑞 男，博士生，1989年7月生

许立忠 男，博士，教授，博士生导师，1962年1月生

TH113.1

A

10.13465/j.cnki.jvs.2017.23.009