基于细菌觅食决策和深度置信网络的滚动轴承故障诊断

陶 洁, 刘义伦, 杨大炼, 宾光富

(1. 中南大学 机电工程学院，长沙 410083；2. 湖南科技大学 知识处理与网络化制造实验室，湖南 湘潭 411201；3. 中南大学 轻合金研究院，长沙 410083；4. 湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201)

基于细菌觅食决策和深度置信网络的滚动轴承故障诊断

陶 洁1,2, 刘义伦1,3, 杨大炼1,4, 宾光富4

(1. 中南大学 机电工程学院，长沙 410083；2. 湖南科技大学 知识处理与网络化制造实验室，湖南 湘潭 411201；3. 中南大学 轻合金研究院，长沙 410083；4. 湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201)

在利用深度置信网络进行滚动轴承故障诊断时，网络结构的设置不仅影响诊断的结果，还影响计算效率。为提高滚动轴承故障诊断的准确率，提出基于细菌觅食决策和深度置信网络的滚动轴承故障诊断方法。该方法利用采集的样本数据对深度置信网络进行训练，以构造细菌觅食决策算法的适应度函数，通过计算各个细菌的适应度来衡量模型的优劣。由于细菌觅食决策算法具有并行搜索能力，能有效选取深度置信网络各隐节点数、学习率、动量等参数，生成合适的分类器提高滚动轴承故障诊断的准确率。实验中，与SVM(Support Vector Machines)、BPNN(Back Propagation Neural Network)、KNN(k-Nearest Neighbor)等方法做比较，所提方法对滚动轴承故障诊断的准确率达到97.83%，能更加高效、准确的识别滚动轴承故障。

深度置信网络；细菌觅食决策算法；滚动轴承；故障诊断

滚动轴承是旋转机械的核心部件，在使用过程中，由于疲劳、磨损、过载、腐蚀等原因，容易造成滚动轴承的损伤[1]。目前，对滚动轴承的故障诊断技术主要集中在信号分析和智能诊断两方面。当滚动轴承发生故障时，振动信号呈现非平稳、非线性的特点，故障特征常常被设备的工作频率、噪声等淹没，因此传统的信号处理与分析很难取得较好的结果[2-3]。在智能诊断方面，主要采用的诊断方法有：支持向量机(Support Vector Machines, SVM)、人工神经网络(Artificial Neural Network, ANN)、流行学习(Manifold Learning, ML)、核方法(Kernel Method, KMs)等模式识别方法[4]。这些方法在机械设备故障诊断中取得了一定的成果，但它们均属于“浅层学习”的算法结构，要在一到两层的模型结构中完成函数拟合，因此故障诊断的结果不稳定[5-6]。

深度学习是一种新兴的机器学习方法，它主要模拟人脑结构，通过层次化学习实现数据的高效处理。Schmidhuber等[7-10]提出的深度置信网络(Deep Belief Network, DBN)及其训练算法，已成为深度学习领域的一个主要模型框架,在语音、图像、手写体识别、多媒体检索等领域取得了良好的效果，并在故障诊断领域得到初步应用。Tran等[11-12]应用DBN对机械设备健康状况进行监测和识别，实验证明DBN能有效识别设备的故障状态。Sun等[13-14]通过信号处理提取监测信号的故障特征，用深度学习实现机械故障类型及故障损伤程度的诊断。单外平等[15]研究了DBN对滚动轴承原始振动信号的重构和特征提取。Shao等[16]提出时域特征提取和粒子群优化的DBN，对滚动轴承进行故障诊断。但以上研究仅凭经验或反复实验对DBN结构参数进行设置，模型优化训练时间长，难以确保故障诊断的准确率。

为提高滚动轴承故障诊断的准确率，减少模型的优化时间，本文提出基于细菌觅食决策算法和深度置信网络的故障诊断方法。利用细菌觅食决策算法(Bacterial Foraging Algorithm, BFA)的并行搜索能力，对DBN的模型参数进行优化选择。该方法采用DBN对样本数据的训练来构造适应度函数，用训练误差阈值作为细菌决策算法迭代的终止条件，将BFA与DBN的参数优化相关联，有效生成合适的分类器提高滚动轴承故障诊断的准确率。

1 DBN基础理论

DBN是一种多隐层的概率生成模型，通过训练各节点间的权值，使整个模型的生成概率最大化。图1是DBN的基本结构，由若干个受限玻尔兹曼机(Restrict Boltzmann machine, RBM)和一个反向传播神经网络(BPNN)组成。其中，RBM是有向连接的两层神经网络，一个RBM的输出作为下一个RBM的输入，不断叠加构成多隐层结构。

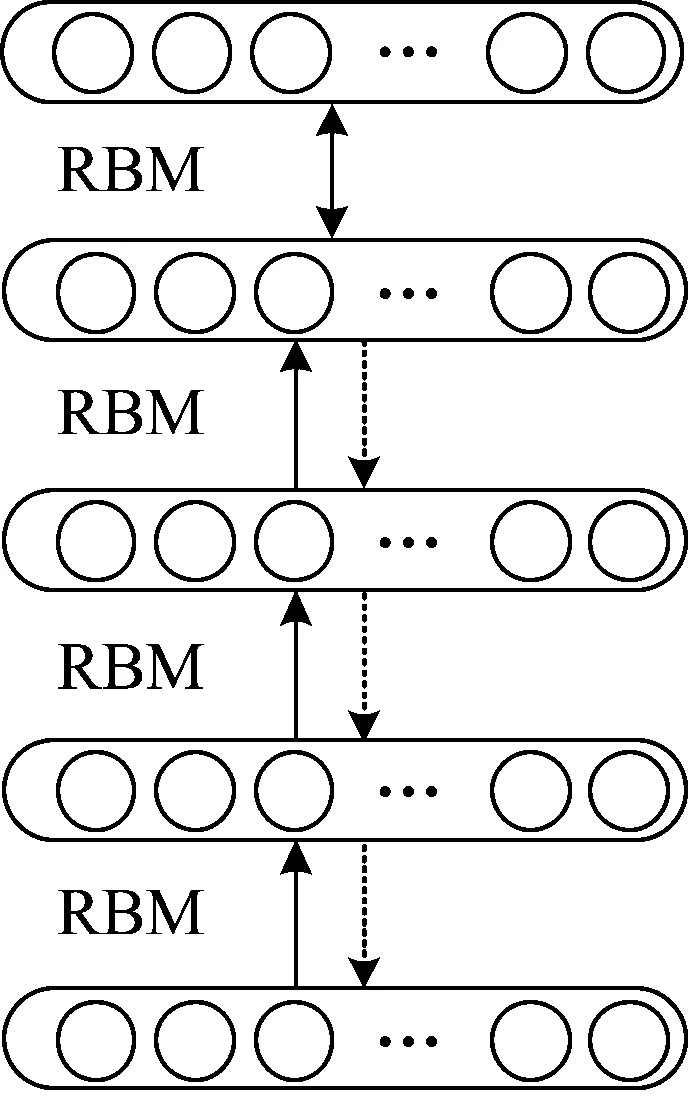
图1 DBN基本结构Fig.1 The basic structure of DBN

RBM的基本结构如图2所示，其中vi为输入层显节点，hi为输出层隐节点，显节点和隐节点有向全连接，而显节点之间以及隐节点之间没有连接。c为输入层的偏置项，b为输出层的偏置项，w为显节点到隐节点的连接权值，b，c，w构成模型的权值集θ。

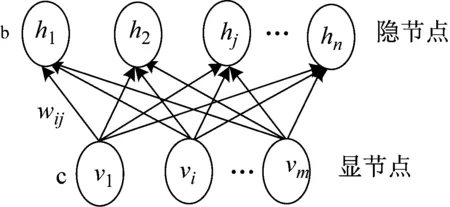
图2 受限玻尔兹曼机Fig.2 Restrict Boltzmann Machine

RBM的能量函数定义为

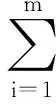
(1)

用能量函数定义显节点和隐节点的联合概率分布函数，其中Z(θ)为配分函数，以实现归一化操作：

(2)

(3)

在RBM中，给定模型输入向量v的值，则输出层隐节点hi的激活概率为

(4)

给定模型输出层向量h的值，输入层显节点vi的激活概率为

(5)

为得到模型的最优解，用训练集(D)的负对数似然函数作为损失函数：

(6)

通过损失函数对参数集(θ)的偏导数更新各个权值，计算公式如(7)，其中<:>d是数据样本统计概率，<:>m是模型的生成概率。

(7)

DBN通过调整各节点权值，使节点的样本统计概率与模型生成概率尽量相等，从而实现数据的预测与分类。DBN的训练分两个阶段：自底向上的逐层训练每个RBM和自顶而下的微调网络权值。在RBM中，数据样本的无偏统计概率可以用公式(4)、(5)计算得到，而模型生成的无偏概率却很难获得。Hinton等提出对比散度算法，通过1次Gibbs采样得到RBM分布的近似值，计算公式如(8)，其中σ为学习率，λ为动量。

(8)

2 基于细菌觅食决策算法的DBN

由于目前深度置信网络的参数设置，缺乏有效的训练算法，在参数选择上主要靠经验或反复实验。BFA是一种基于并行搜索的全局优化算法，具有群体智能特性，易跳出局部极值找到最优解[17]。因此BFA为解决DBN的参数设置问题，提供了有效的途径。图3是BFA对深度置信网络优化的过程。选取S个细菌，同时对DBN的隐节点数、学习率和动量并行搜索。其中Nc、Nre、Ned分别表示趋向、复制、迁移操作需要执的次数，i，j，k分别表示三个操作的计数参数。

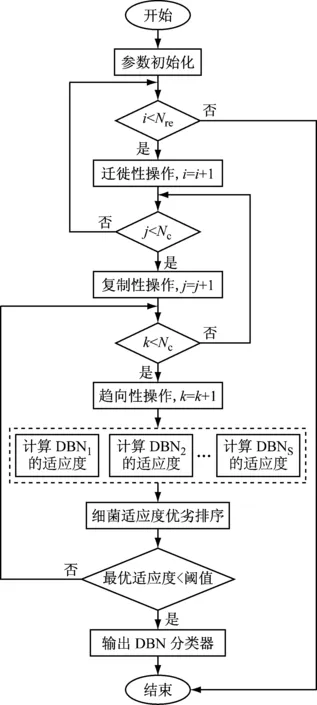
图3 基于细菌觅食决策算法的优化流程图Fig.3 Optimization flow chart of bacterial foraging algorithm

BFA-DBN参数优化流程如下：

(1)初始化BFA的参数Nc、Nre、Ned、S，设置DBN隐层数l，隐节点数n，学习率a，动量m的解析空间；

(2)在解析空间内随机产生S个细菌，计算每个细菌的适应度；

(3)若细菌的适应度小于阈值，则输出DBN产生分类器，否则执行趋向、复制或迁移操作；

(4)令Pt(i,j,k)为第t个细菌，执行完第i次趋向性操作、第j次复制操作和第k次迁移操作后的位置：

Pt(i+1,j,k)=Pt(i,j,k)+Ct(i,j,k)V(i,j,k)

(9)

式中：Ct(i,j,k)为细菌前进和翻转运动的步长；Vt(i,j,k)为随机产生的方向向量。

Ct(i,j,k+1)=Ct+1(i,j,k+1)/M1

(10)

Ct=(i,j+1,k)=[max(F(i,j,k))-

min(F(i,j,k))]/M2

(11)

式中：M1为第t个细菌执行趋向性操作的次数；M2为比例缩放因子；若第t个细菌个体没有发生迁徙操作，则

Ct(i+1,j,k)=Ct(i,j,k)

(12)

否则Ct(i+1,j,k)=Ct+1(i,j+1,k)

(13)

(5)计算新种群中各细菌个体的适应度，若训练误差小于阈值，则输出DBN生成分类器，否则重复(3)～(4)过程，直至迭代结束。

实现细菌觅食决策算法寻找全局最优解的关键是，确定适应度函数和终止条件[20]。本文采用样本数据对DBN的训练来构造细菌觅食决策算法的适应度函数，并设置训练误差的阈值作为BFA迭代的终止条件，计算步骤如下：

(1)令第t个细菌的适应度为Pt=(lt,nt,at,mt)，则DBN的第一隐层节点数为nt，第二隐层节点数为lt，学习率为at，动量为mt，初始化DBN参数集θ;

(2)v0为输入样本向量，d为DBN迭代次数，e为DBN的训练误差；

(3)利用公式(4)、(5)计算RBM各显层和隐层的特征向量h0，v0，h1，v1，…，hlt；

(4)利用公式(7)得到RBM初始状态与更新状态下联合概率分布，代入公式(8)修正参数集θ；

(5)用随机批处理对训练集迭代d次，重复(3)～(4)过程；

(6)用BPNN微调各隐层参数的权值θ。

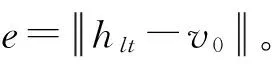
通过适应度函数，将细菌觅食决策算法的并行搜索与DBN的参数优化相关联，其中适应度的高低可以有效衡量DBN模型的优劣，从而产生合适的故障诊断分类器，提高滚动轴承的故障诊断精度。

3 滚动轴承振动测试实验

为验证所提方法的可行性和有效性，本文采用HRB公司生产的NU205圆柱滚动轴承，进行故障诊断实验。为模拟轴承轻微故障和严重故障，分别对滚动轴承内圈、外圈进行点蚀和线切割加工。如图4所示，点蚀故障直径为0.5 mm，线切割故障宽度为0.5 mm，长度为12 mm。

(a) 正常滚动轴承

(b) 内圈点蚀直径 0.5 mm

(c) 内圈线切割直径 0.5 mm

(d) 外圈点蚀直径 0.5 mm

(e) 外圈线切割直径 0.5 mm图4 实验滚动轴承Fig.4 Rolling bearings of experiments

利用QPZZII旋转机械故障实验台及德维创信号采集仪，采集滚动轴承工作状态下的振动信号。实验台如图5所示，主要由电机、皮带轮、传动支座、联轴器、轴承座组成。试件轴承安装在轴承座内，传感器垂直安放在轴承座上方。

图5 旋转机械故障模拟实验台Fig.5 Rotating machinery fault simulation test bench

实验中，轴承转速为1 200 r/min，载荷为500 N，采样频率为10 kHz，采样时长6 s。五个试件的振动信号时域波形，如图6所示。

实验中，滚动轴承外圈与轴承座过盈配合，内圈与转轴相连，滚动轴承随转轴同步旋转。当滚动轴承存在局部损伤时，会引起振动信号突变产生相应的冲击特征。但实验中试件故障比较相似，引起的冲击特征经过轴承座、滚动体、保持架后，能量会衰减损耗，因此各振动信号中的冲击特征比较接近，难以区分滚动轴承的各种故障。

4 实验结果与分析

每次实验，传感器采集60 000个振动加速度信号，顺序截取500个信号，构成1个数据样本。每种试件的振动信号构成120个数据样本，随机选择100个样本作为训练样本，剩下20个作为测试样本。五种试件的振动信号，构成500×500的训练集和500×100的测试集。

(a) 正常滚动轴承

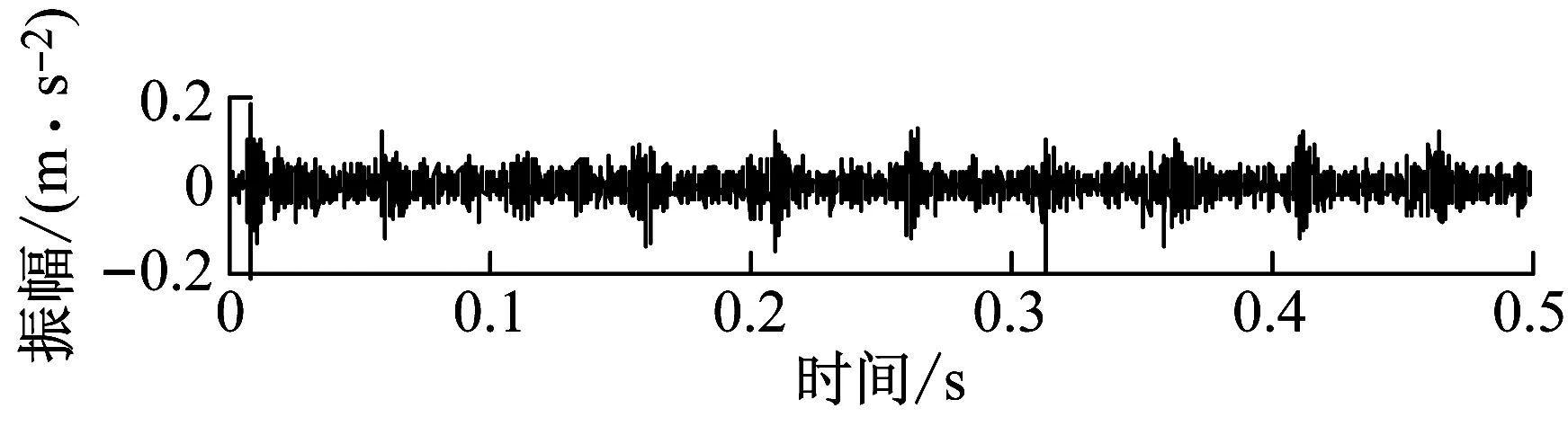
(b) 内圈点蚀直径0.5 mm

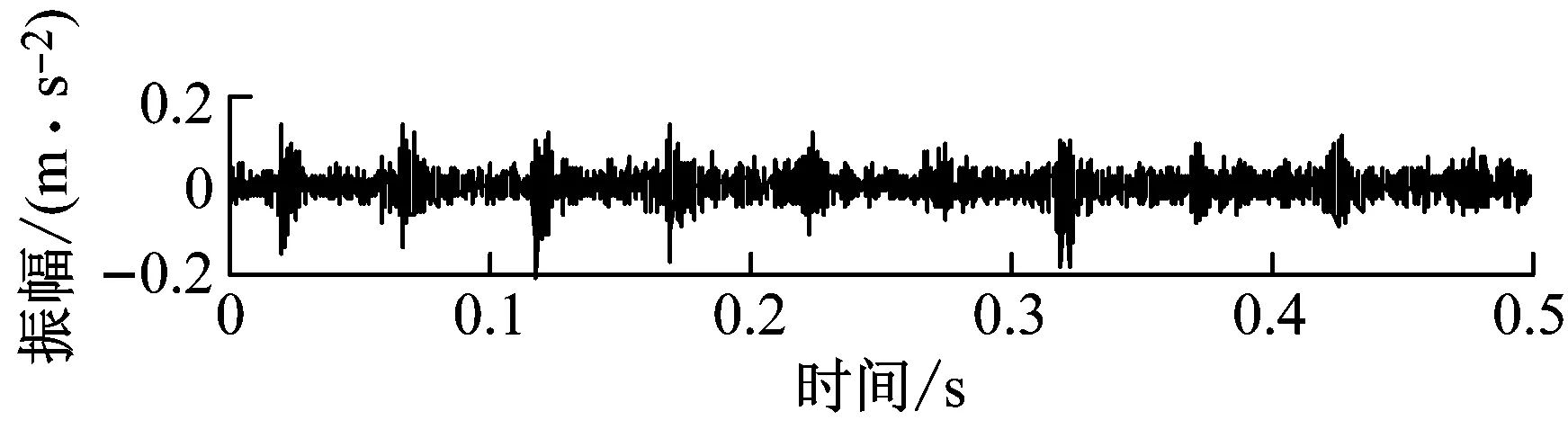
(c) 内圈线切割直径0.5 mm

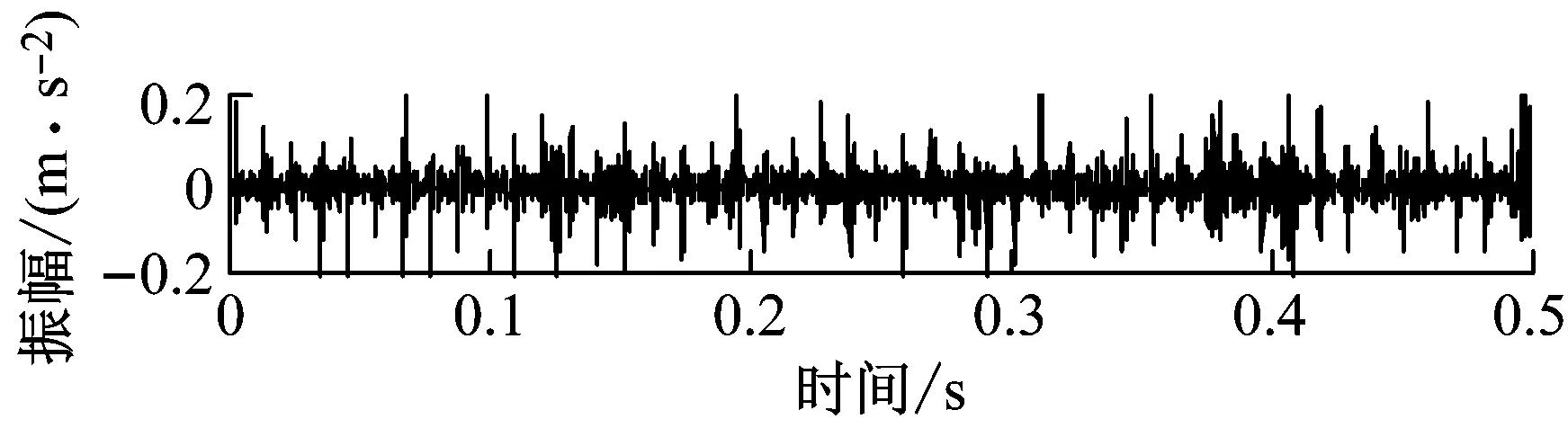
(d) 外圈点蚀直径0.5 mm

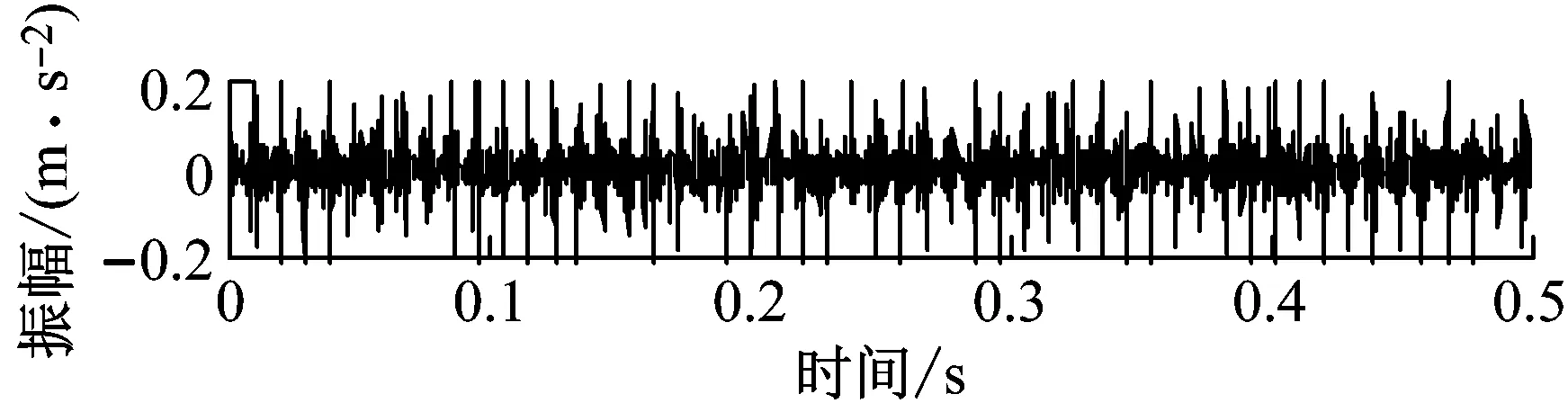
(e) 外圈线切割直径0.5 mm图6 滚动轴承振动信号时域图Fig.6 Rolling bearing vibration signal time domain diagram

4.1 BFA-DBN逐层特征分析与结果比较

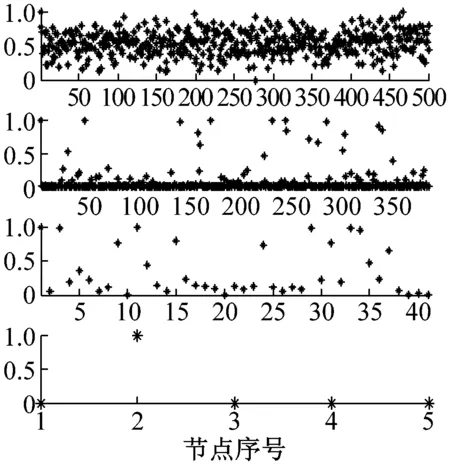
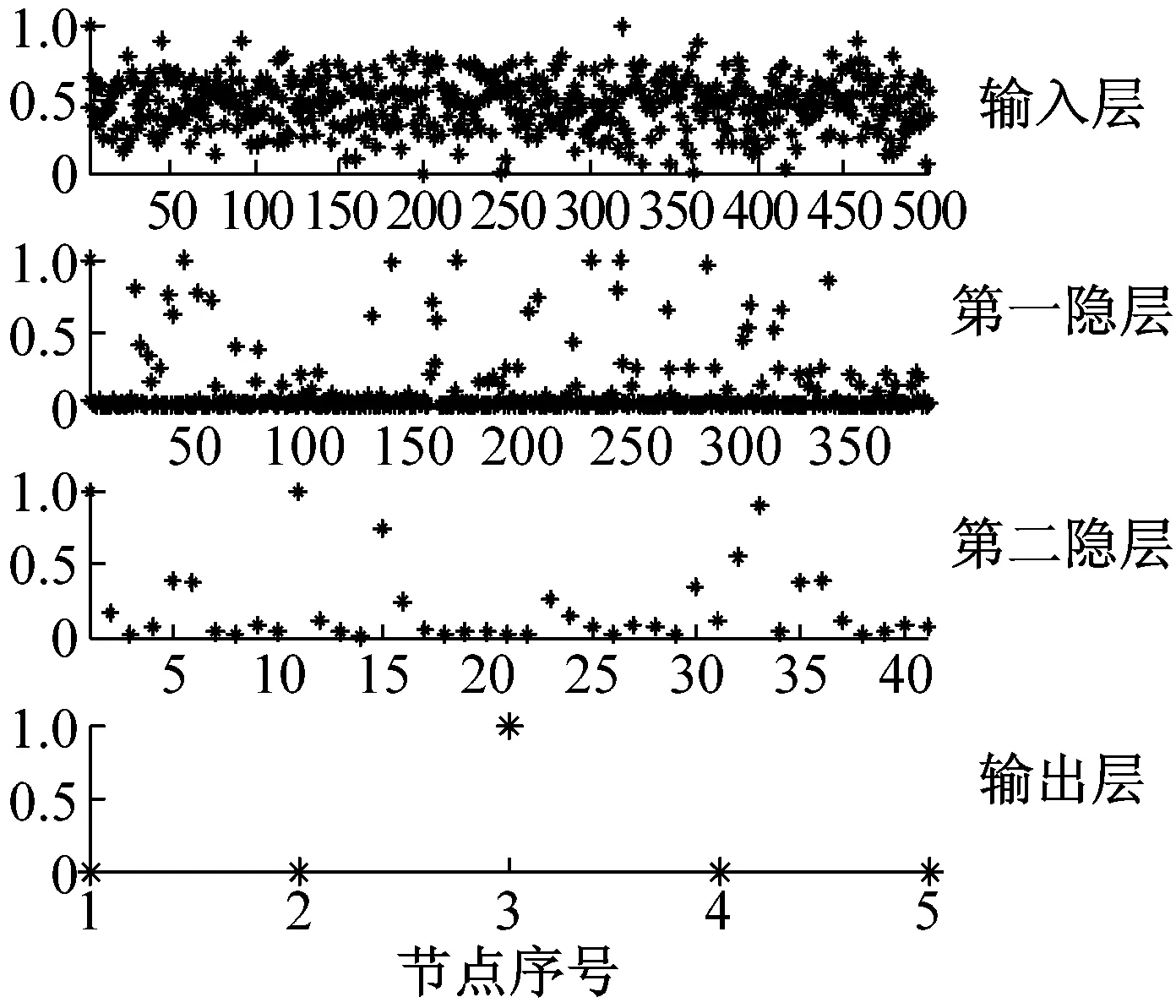
深度学习能通过多层网络结构，直接从原始信号中自动提取故障特征，完成轴承故障诊断。实验中DBN的参数由BFA得到，模型结构参数为500-387-41-5，学习率为0.062 9，动量系数为0.047 8。根据本文2中的训练过程，BFA-DBN对各节点的权值及偏置进行无监督学习，生成DBN故障诊断分类器。各种测试样本经BFA-DBN逐层特征提取情况，如图7所示。

由图7可知，五种样本的原始输入向量特征信息杂乱无章，经第一隐层映射后，输入向量维度由500降到378，且大部分节点激活值为0。经第二隐层映射后，输入向量维度减至41，特征信息进一步集中到激活值较大的节点处。经第三次映射后，输入向量在输出层成功激活相应类别节点(正常轴承1号节点，内圈点蚀故障2号节点，内圈线切割故障3号节点，外圈点蚀故障4号节点，外圈线切割故障5号节点)，完成轴承故障诊断。

(a) 正常轴承

(b) 内圈点蚀直径0.5 mm

(c) 内圈线切割直径0.5 mm

(d) 外圈点蚀直径0.5 mm

(e) 外圈线切割直径0.5 mm图7 测试样本特征提取散点图Fig.7 Feature extraction scatter plot of test samples

为验证本文所提方法(DBN-BFA)的有效性，与传统的特征提取和模式识别(SVM、KNN、BPNN)方法做比较。从振动信号中提取常用的轴承诊断特征：脉冲因子、峭度因子、峰值因子、波形因子、峭度、均方根、峰-峰值、平均值、方差、方差、标准差、裕度因子、最大值、最小值(14-features)、本征模函数能量熵(imf)。其中，支持向量机(SVM)采用径向核函数，惩罚因子及核参数由遗传算法得到；最邻近距离分类器(KNN)采用欧式距离作为判别标准；单层人工神经网络(BPNN)的结构为14-8-5；多层人工神经网络(BPNN)的结构为14-8-6-5。实验重复10次，各种方法对测试集进行分类识别，结果如图8所示。

由图8可知，本文所提方法(BFA-DBN)对滚动轴承故障诊断的平均准确率达到97.83%，10次实验的标准差为1.57%，表现出良好的稳定性和泛化能力。传统的故障诊断方法SVM-imf、KNN-14-feature对滚动轴承故障诊断的平均准确率分别为71.33%和78.67%。而单隐层和多隐层的人工神经网络(BPNN-feature-14)对信号的分类准确率仅为40%左右。传统的模式识别方法主要基于“浅层学习”，需要对振动信号做特征提取以降低样本维度。对于不同损伤程度的振动信号，传统的信号处理或特征提取方法的自适应能力不强，故障特征信息提取不完整，从而影响故障诊断的准确率。其中，多隐层的BPNN也采用了深层结构，但由于BPNN的多隐层结构不具备无监督学习能力，依靠BP算法对模型进行训练，模型的误差可能收敛，也可能陷入局部极值，使得分类准确率波动较大。

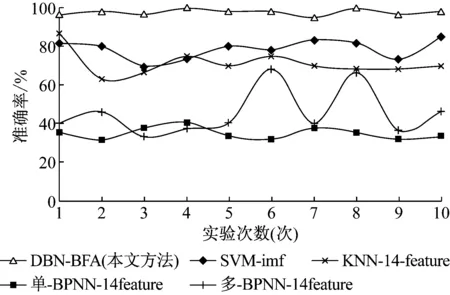
图8 10次实验中各方法的分类准确率Fig.8 The identify results of 10 times experiments

4.2 BFA优化过程及分析

为验证BFA的性能，用逐层优化算法(Layer-by-layer Optimization Algorithm, LOA)和粒子群优化算法(Particle Swarm Optimization Algorithm, PSO)进行对比实验。设DBN学习率、动量系数的解析空间为[0, 0.1],隐节点数的解析空间为[5,500]，DBN训练误差阈值为0.05。BFA-DBN的细菌种群数为20，趋向、复制、迁徙的操作数为5，迁徙概率为0.1。逐层优化算法(LOA-DBN)中，隐节点数的优化步长为5。粒子群优化算法(PSO-DBN)的种群数量为20，迭代次数为50，学习因子为2，惯性权重为0.8。DBN各隐层的节点数、学习率、动量，由BFA、LOA、PSO分别进行优化得到，结果如表1所示。

表1 各种算法对DBN模型优化的结果Tab.1 The structures of DBN based on the optimization algorithms

由表1可知，本文所提方法(BFA-DBN)经过7次种群迭代(每次迭代计算20个细菌的适应度)，共用时246.759 s完成DBN的优化，故障诊断准确率为97.83%。LOA-DBN通过步长和多层嵌套循环来优化模型结构，经过238次迭代，用时549.562 s，分类准确率为95.25%。PSO-DBN用20个种群经过9次迭代，用时328.468 s，得到模型分类准确率为96.28%。BFA、LOA、PSO都是通过搜索，对模型进行优化。但LOA主要依靠步长，在空间内对各个解逐步计算以寻找最优值，因此用时较长、精度较低。PSO通过比较局部极值和全局极值进行并行搜索，但种群代数达到一定值时，分类准确率不再提高，从而陷入局部极值。BFA是仿生物学的智能算法，通过并行计算和迁徙操作，不仅能跳出局部极值，还会逐渐向最优值靠近。图9是BFA对隐节点数优化过程中，部分迭代状态下的细菌种群分布情况。

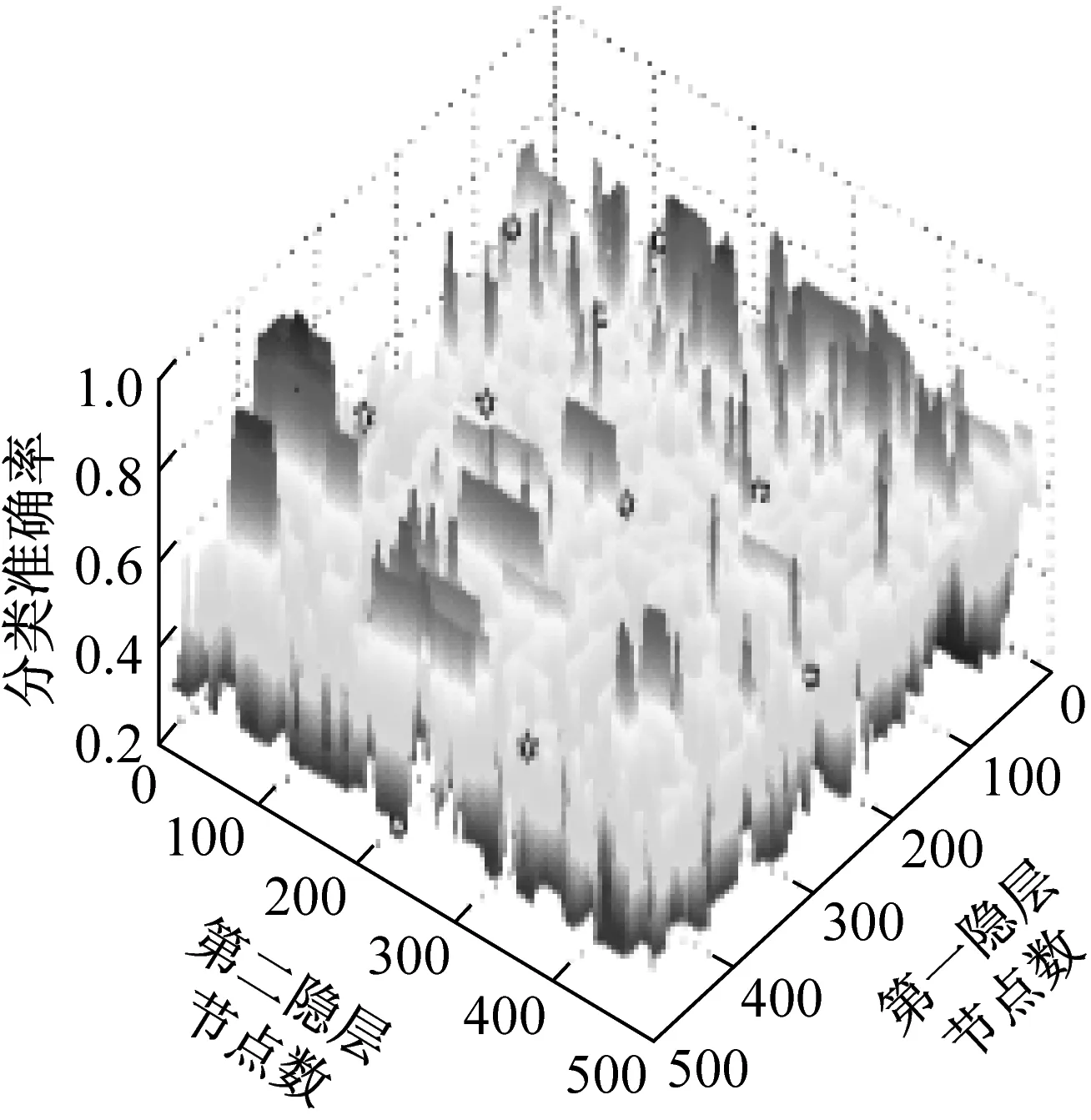
(a) 初始种群分布

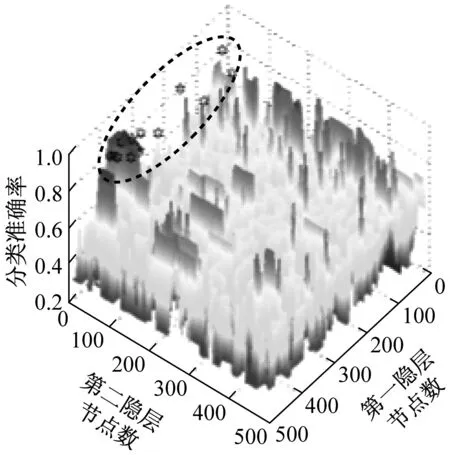
(b) 第5代种群分布

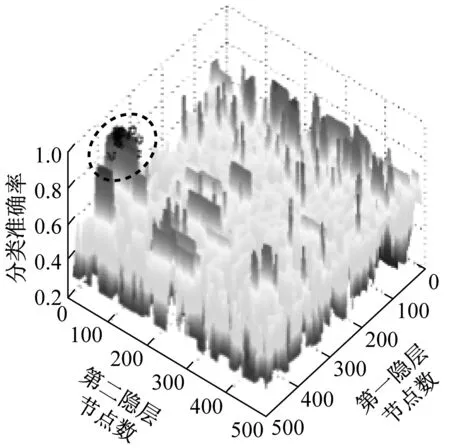
(c) 第7代种群分布图9 BFA优化过程中细菌种群分布Fig.9 The distribution of bacteria in the BFA optimization process

如图9所示，细菌个体在搜索过程中获得与解有关的信息，通过复制、趋向操作细菌种群逐渐向最优解区域聚集。同时，BFA按指定概率执行迁徙操作，当问题的解空间存在多个极值点时，符合迁徙条件的细菌被随机分配到解析空间中，用新的个体来代替原有的个体，避免种群陷入局部极值。实验中，BFA初始种群在解析空间内随机分布，随着种群的迭代，细菌逐步向最优解靠近，经过7次种群迭代，找到模型的最优解。从细菌觅食决策算法来看，引入复制、趋向和迁徙操作可以提高算法的全局搜索能力。因此，DBN-BFA用较少的时间就能完成模型优化，提高故障诊断的精度。

5 结 论

(1) 本文采BFA-DBN直接对滚动轴承原始振动信号进故障诊断，简化了传统故障诊断中的特征提取过程，避免了模式识别对信号处理、特征提取结果的依赖。

(2) 采用DBN对样本数据的训练误差构造BFA的适应度函数，有效选取DBN的参数，克服了人为经验设置或反复实验的不足。与传统的优化算法相比，细菌觅食决策算法的并行搜索能力和迁徙操作，能减少搜索时间，提高故障诊断的精度。

(3) 由于时间关系，本文仅对滚动轴承不同故障类型及损伤情况做分类识别，对滚动轴承早期微弱故障的诊断还有待研究。

[1] 郭亮, 高宏力, 张一文, 等. 基于深度学习理论的轴承状态识别研究[J]. 振动与冲击, 2016, 35(12): 166-170.

GUO Liang, GAO Hongli, ZHANG Yiwen, et al. Research on bearing condition monitoring based on deep learning[J]. Jouranl of Vibaration and Shock, 2016, 35(12): 166-170.

[2] EL-THALJI I, JANTUNEN E. A summary of fault modelling and predictive health monitoring of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2015, 60: 252-272.

[3] BIN G F, GAO J J, LI X J, et al. Early fault diagnosis of rotating machinery based on wavelet packets—empirical mode decomposition feature extraction and neural network[J]. Mechanical Systems and Signal Processing, 2012, 27: 696-711.

[4] 王国彪, 何正嘉, 陈雪峰, 等. 机械故障诊断基础研究 “何去何从”[J]. 机械工程学报, 2013, 49(1): 63-72.

WANG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Basic research on machinery fault diagnosis-What is the prescription[J]. Journal of Mechanical Engineering, 2013, 49(1): 63-72.

[5] 文成林,吕菲亚，包哲静，等.基于数据驱动的微小故障诊断方法综述[J].自动化学报,2016, 42(9):1285-1299.

WEN Chenglin, LÜ Feiya, BAO Zhejing, et al. A review of data driven-based incipient fault diagnosis[J]. Acta Automatica Sinica, 2016, 42(9): 1285-1299

[6] 雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康监测方法[J]. 机械工程学报, 2015, 51(21):49-56.

LEI Yaguo, JIA Feng, ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering, 2015, 51(21): 49-56.

[7] SCHMIDHUBER J. Deep learning in neural networks: An overview[J]. Neural Networks, 2015, 61(9): 85-117.

[8] HINTON G, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554.

[9] ERHAN D, BENGIO Y, COURVILLE A. Why does unsupervised pre-training help deep learning[J]. Journal of Machine Learning Research, 2010,11(3): 625-660.

[10] HINTON G, SALAKHUTDINOV R. Reducion the dimensionality of data with neural networks[J]. Science, 2006, 313: 504-507.

[11] TRAN V T, ALTHOBIANI F, BALL A. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaeser energy operator and deep belief networks[J]. Expert Systems with Application, 2014, 41(9): 4113-4122.

[12] TAMILSELVAN P, YIBIN W, PINGFENG W. Deep belief network based state classification for structural health diagnosis[J]. Reliability Engineering and System Safety, 2013, 115(3): 124-135.

[13] SUN J, WYSS R, STEINECKER A, et al. Automated fault detection using deep belief networks for the quality inspection of electromotors[J]. tm-Technisches Messen, 2014, 81(5): 255-263.

[14] GAN M, WANG C, ZHU C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2016, 72: 92-104.

[15] 单外平, 曾雪琼. 基于深度信念网络的信号重构与轴承故障识别[J].电子设计工程,2016,24(4):67-71.

SHAN Waiping， ZENG Xueqiong. Signal reconstruction and bearing fault identification based on deep belief network[J]. Electronic Design Engineering,2016,24(4):67-71.

[16] SHAO H, JIANG H, ZHANG X, et al. Rolling bearing fault diagnosis using an optimization deep belief network[J]. Measurement Science & Technology, 2015, 26(11): 115002.

[17] PASSINO K M. Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine，2002，22：52-67.

[18] 杨大炼, 刘义伦, 李学军, 等. 基于细菌觅食优化决策的齿轮箱故障诊断[J]. 中南大学学报(自然科学版), 2015, 46(4): 1224-1229.

YANG Dalian, LIU Yilun, LI Xuejun, et al. Gearbox fault diagnosis based on bacterial foraging algorithm optimization decisions[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1224-1229.

[19] 胡洁. 细菌觅食优化算法的改进及应用研究[D]. 武汉: 武汉理工大学, 2012.

[20] 周雅兰. 细菌觅食优化算法的研究与应用[J]. 计算机工程与应用, 2010, 46(20):16-21.

ZHOU Yalan. Research and application on bacteria foraging optimization algorithm[J]. Computer Engineering and Applications, 2010, 46(20):16-21.

Rollingbearingfaultdiagnosisbasedonbacterialforagingalgorithmanddeepbeliefnetwork

TAO Jie1,2, LIU Yilun1,3, YANG Dalian1,4, BIN Guangfu4

(1.College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. Lab of Knowledge Processing and Networked Manufacturing, Hunan University of Science and Technology, Xiangtan 411201, China;3. Light Alloy Research Institute, Central South University, Changsha 410083, China; 4. Hunan Provincial Key Lab of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan 411201, China)

When studying rolling bearing fault diagnosis with the deep belief network method, parameters in the deep belief network have a great effect on fault diagnosis results and it is hard to obtain suitable parameters. Here, the fault diagnosis method based on the bacterial foraging algorithm and the deep belief network was proposed to improve the correct rate of bearing fault diagnosis. The parallel search ability of the bacterial foraging algorithm was adopted to effectively choose the number of hidden layer, the number of hidden nodes, the learning rate in a deep belief network. The deep belief network’s training data classification error was used to calculate the fitness function of the bacterial foraging algorithm to build an appropriate fault classifier and finish rolling bearing fault diagnosis. The test results showed that the correct rate of the proposed method for rolling bearing fault diagnosis reaches 98.5%; compared with BPNN, SVM and KNN methods, the proposed method can more stably and more accurately identify rolling bearing faults.

deep belief network; bacterial foraging algorithm; rolling bearings; fault diagnosis

国家自然科学基金(51575176；11702091)；湖南科技大学机械设备健康维护湖南省重点实验室开发(201605)

2016-11-14 修改稿收到日期：2017-03-13

陶洁 女，博士生，讲师，1980年12月生

刘义伦 男，教授，博士生导师，1955年10月生

TAH133.33

A

10.13465/j.cnki.jvs.2017.23.011