柔性相似子结构的参数失调与振动控制研究

罗亚军， 徐明龙， 张 帅， 张希农

(西安交通大学 机械结构强度与振动国家重点实验室，西安 710049)

柔性相似子结构的参数失调与振动控制研究

罗亚军， 徐明龙， 张 帅， 张希农

(西安交通大学 机械结构强度与振动国家重点实验室，西安 710049)

典型柔性相似结构的耦合动力学建模与参数失调下系统的振动控制问题对航天结构设计具有重要意义。基于拉格朗日法和最小二乘法，完成了系统的耦合动力学建模和响应解耦处理，并进一步建立了柔性相似结构参数失调情况下的振动主动控制模型。最后完成了相关仿真分析，研究了结构参数失调情况下的系统模态局部化问题，振动控制仿真结果表明本文提出的基于响应解耦实现参数失调情况下系统的振动控制具有显著效果。

柔性相似结构；参数失调；模态局部化；振动控制

航天器通常由桁架、梁、板、壳等结构简单组成在一起，随着科学技术的发展，航空航天工程中出现了许多前所未有的大型柔性对称附件结构，如大展翼太阳能帆板[1]、大口径卫星天线[2]、大型桁架等挠性子结构、具有较大几何尺寸的宇航空间站构件等。这些附件通常都是理想化的完全对称周期结构，但是实际生产制造过程中由于材料缺陷、制造误差、使用过程中的磨损等因素，造成了周期性结构的子结构并不完全对称的现象，理论及实验研究均表明，这种并不完全对称造成的参数失调对大型天线等弱耦合周期结构的动力学特性产生比较大的影响，可能使结构出现模态局部化现象[3-5]。杨智春等[6-7]开展了大型飞机尾翼中T尾结构的模态局部化判据研究，以及模态局部化对飞机T尾结构颤振特性的影响。苏继龙等[8]也对飞机机翼这类弱耦镜像对称工程结构的模态局部化度的结构参数表征进行了判据研究。通常，模态局部化会导致能量的不均匀分布，如果能量高度集中在系统的局部位置可能会导致整体结构的破坏[9]。李凤明等[10]还对典型周期结构因失谐引起的结构模态局部化问题研究进行了综述，并提出了振动局部化理论如何在振动控制中应用等展望分析。

航天工程的柔性相似结构中，在参数失调情况下耦合动力学系统出现危害性的振动能量转换，从而引起振动危害，这需要通过解耦和控制来解决该问题。当前在多自由度振动理论分析中，耦合动力学方程中常表现为动力学矩阵的非对角线元素出现非零值，这类方程不方便直接求解，而常常需要通过坐标转换使得非对角线元素化为零值，实现模型的解耦才能方便求解[11]。在耦合动力学系统的解耦和控制方面同样可以借鉴该思路。刘相秋等[12]还提出一种预测控制方法，针对失谐前后的星载天线结构进行了振动控制仿真研究，控制效果较好，且相比LQR控制方法无需加激振。

柔性相似结构模型中如果出现参数失调，耦合系统的主体姿态运动将因模态局部化问题出现多阶模态频率耦合的现象。对于该问题，一方面应该对具有模态耦合的姿态运动振动信号进行解耦分析，另一方面应该完成对不需要的模态响应进行控制。本文将基于最小二乘法实现姿态响应信号的解耦，并基于解耦信号进行姿态运动的振动控制。

1 典型柔性相似结构的建模

1.1 模型介绍

如图1是一个典型的柔性相似结构模型，其由一个航天器中心刚体加柔性附件构成，附件被模型化成固接于中心刚体的悬臂梁，坐标系X0Y选取在固连于中心刚体的质心位置，附件分别位于正负X轴。附件长度均为L，附件弯曲刚度分别是EI1，EI2，质量线密度分别是m1、m2，附件在坐标系内沿着Y方向有横向位移，分别为w1(x,t)，w2(x,t)，中心刚体的转动惯量为I0，姿态角为θ。

1.2 耦合动力学建模与理论求解

通常，航天器中心刚体存在姿态转动，而两个相似柔性附件将同时因中心刚体的姿态转动而存在刚体运动，其次本身还存在弹性弯曲振动。因此系统是一个典型的刚-柔耦合动力学系统，一般可利用拉格朗日法建立其动力学方程。

图1 典型的柔性相似结构模型Fig.1 Typical flexible similar structure

首先分析系统的动能T，它由中心刚体、附件1和附件2三个部分的动能组成，即：

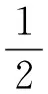
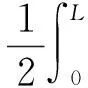
(1)

两个附件各自的动能分别是由中心刚体姿态运动引起的刚体动能和本身的振动引起的动能之和，这也是当前系统刚柔耦合特性的主要存在根源。系统势能也由三个部分组成，即：

(2)

由于柔性附件的质量轻，与中心刚体相比可以忽略不计，所以不考虑其耗散能。而中心刚体本身常被施加阻尼性质的控制项，因此系统的耗散能来源于中心刚体，即：

(3)

将附件的弹性位移展开为广义坐标的形式为：w1(x,t)=φ1q1,w2(x,t)=φ2q2，且每个附件仅考虑其一阶局部模态的影响，q1和q2分别为两附件的广义坐标，φ1和φ2为悬臂梁的一阶振型，进一步便可以写出广义坐标下的T，V，D。由拉格朗日方程，可得

(4)

式中，qj表示θ、q1和q2三个自由度，能量表达式对三个自由度分别求导并整理可得系统的动力学方程：

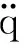
(5)

式中，

(6)

C=diag(cθ,0,0)

(7)

(8)

由模态分析可以得到系统的主振型Φ，进行坐标变换，有模态坐标表达的方程为

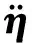
(9)

式中，Mp=ΦTMΦ，Cp=ΦTCΦ，Kp=ΦTKΦ。设系统的初始条件为q0，则主坐标下的初始条件为

(10)

(11)

式中，

ξi=Cpi/(2ωiMpi)

(12)

系统在主坐标下的响应为

ηi(t)=e-ξiωit[ηi(0)cosωdit+

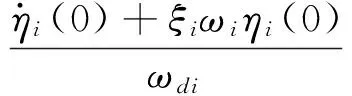
(13)

式中，ωdi是第i阶阻尼固有频率：

(14)

若初始条件中广义速度为零，则

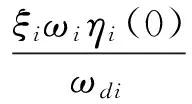
(15)

所以，阻尼耦合系统的物理坐标下的响应为

q=Φ{η1η2η3}T

(16)

1.3 参数失调模型的响应信号解耦与振动控制

耦合系统主坐标的理论解为

(17)

如果令

(18)

则姿态转角响应θ的拟合信号可以表示为

(19)

式中:ξi，ωi可由θ(t)的幅频响应分析求出，而系数b11、b12和b13按理论描述均为系统的特征参数，可以通过最小二乘法拟合获得，从而实现姿态信号的解耦。通过对姿态信号的解耦，可以分离出来非姿态模态信号，即第2、3阶频率信息。则可以设计振动控制算法，设法抑制该两阶频率信息。

设u0(t)为分离出来的仅含一阶模态信息的分离信号，即

u0(t)=b11f(ξ1,ωd1)=b11e-ξiωit[cosωdit+

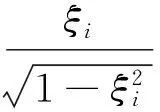
(20)

则有转角信号中的干扰信号为

u(t)=θ(t)-u0(t)

(21)

如果以干扰信号作为反馈源信号，并采样比例速度负反馈控制律设计方法，则有控制系统方程为

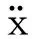
(22)

2 数值仿真

2.1 模态数值分析

设仿真模型的参数如下：m1=m2=0.03 kg/m，I0=1 000 kg·m2，L=10 m，kθ=500 N·m/rad，cθ=50 N·s/rad，EI1=EI2=15 N/m。表1给出了柔性附件2中弯曲刚度EI2出现刚度失调时的系统固有频率结果。

图2给出耦合系统的模态振型图。可发现耦合系统前三阶模态振型依次分别为姿态振型、同向模态振型和反向模态振型。

2.2 系统参数失调数值仿真分析

下面开展系统振动响应分析，仿真时系统具有非零初始位移条件。图3为耦合系统无失调时的仿真分析结果，图中分别给出转角和两个柔性附件的广义位移响应，以及系统总体动能变化的时域曲线。从图中可以看到耦合系统的姿态响应在阻尼效果下在200 s内衰减趋于0，之后为两个柔性附件的稳态振动，系统的总能量趋于稳定，且系统的总能量主要为两个柔性附件的振动能量。

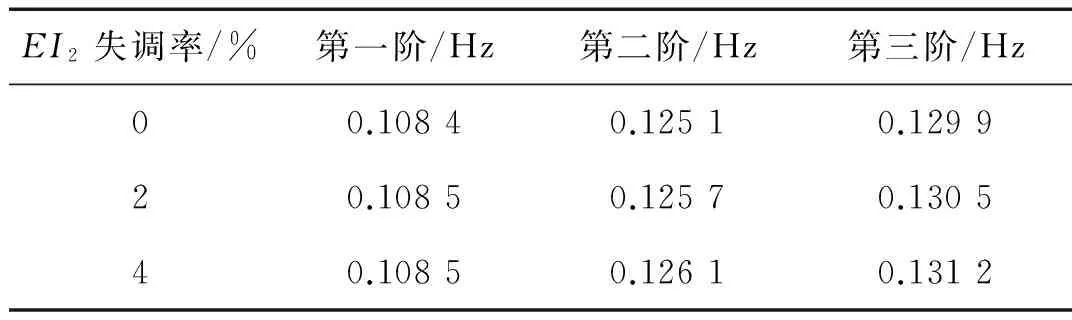
表1 柔性附件2中弯曲刚度参数失调时耦合系统的固有频率Tab.1 Natural frequency of coupling system withdetuned parameter (EI2)

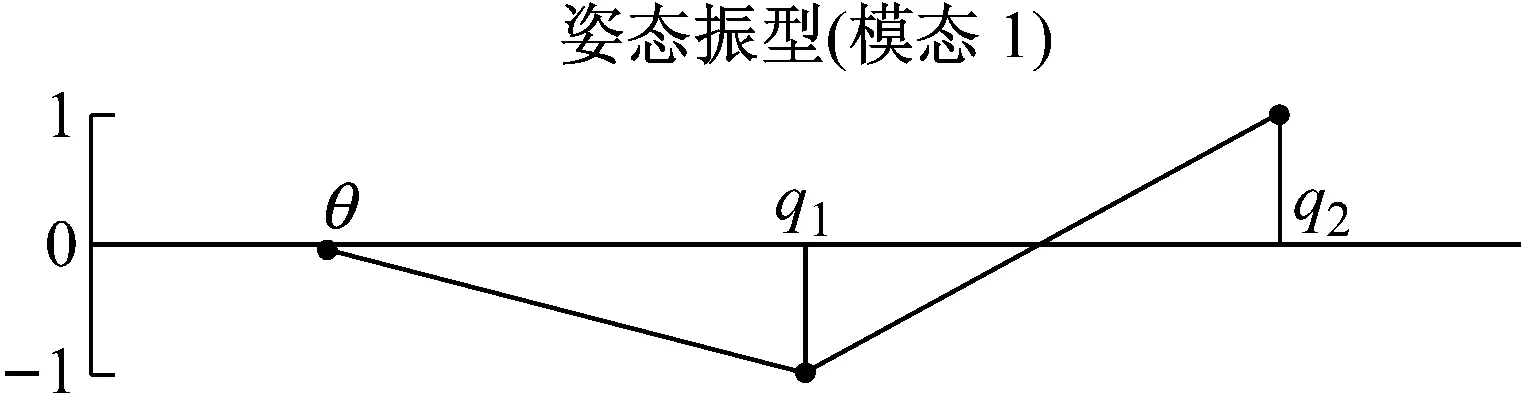
图2 柔性相似结构的模态振型图Fig.2 Modal shapes of flexible similar structure

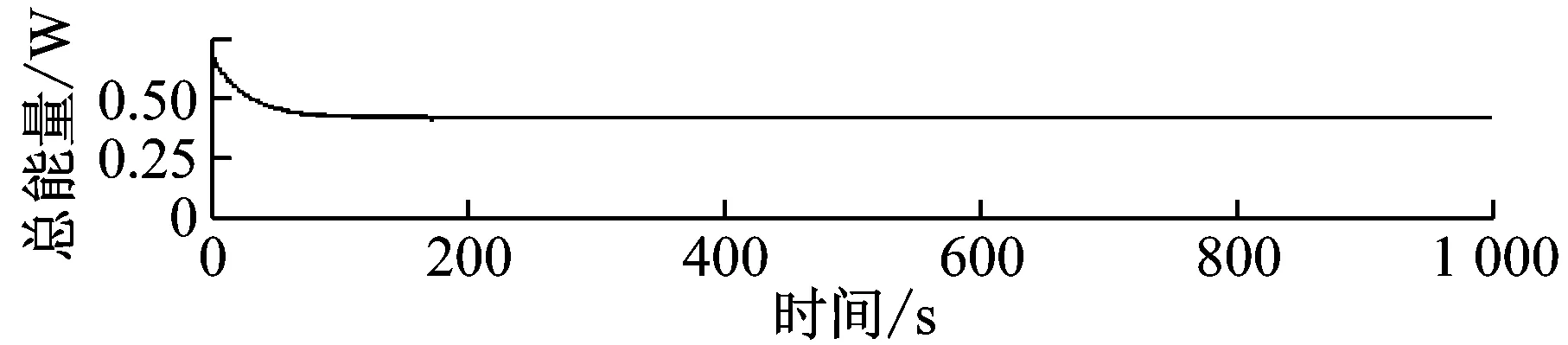
图3 无参数失调时系统的响应曲线Fig.3 Response curves without parameter detuning

图4进一步给出了耦合系统三个广义位移的幅频曲线，从该图可以发现转角响应中仅含一阶频率信息，且阻尼效果显著，姿态响应幅值谱峰值位置因阻尼的存在而非常平缓。而两个柔性附件的振动响应幅值谱曲线相同，幅值谱曲线均在0.125 1 Hz达到1.456 m的峰值。

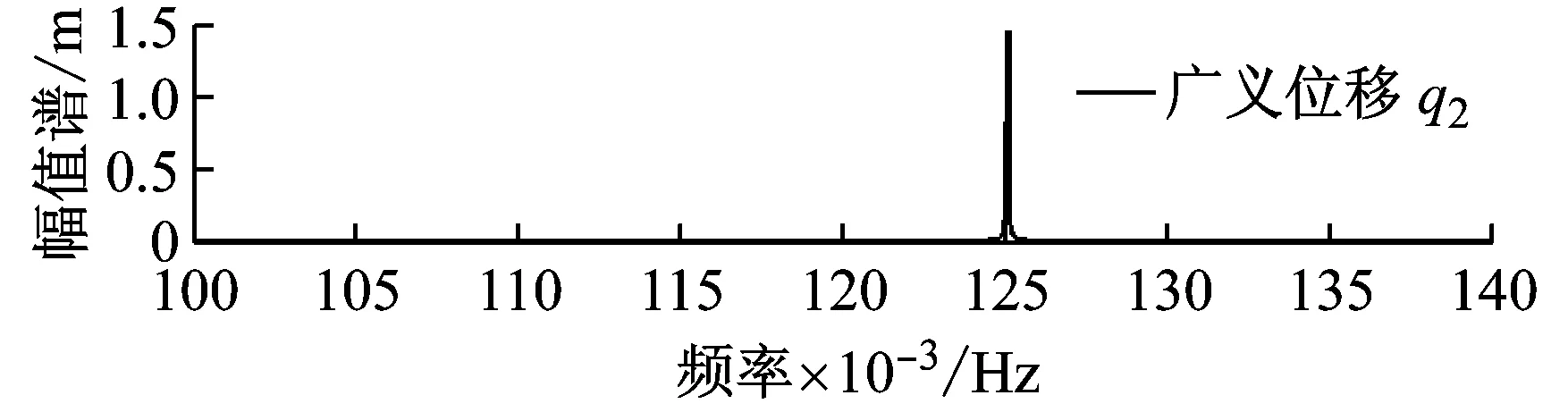
图4 无参数失调时系统的响应幅值谱曲线Fig.4 Response spectrum curves without parameter detuning

图5给出了柔性附件2的弯曲刚度EI2出现2%失调时的仿真结果，图6给出了相应的幅值谱仿真结果。图5显示参数失调后姿态运动经历初始的大幅衰减后呈现小幅的持续振荡。两个柔性附件的广义位移也不再一致，而出现了显著差异，即发生模态局部化现象。系统的总能量曲线也不再趋于稳定，而是持续的减少。

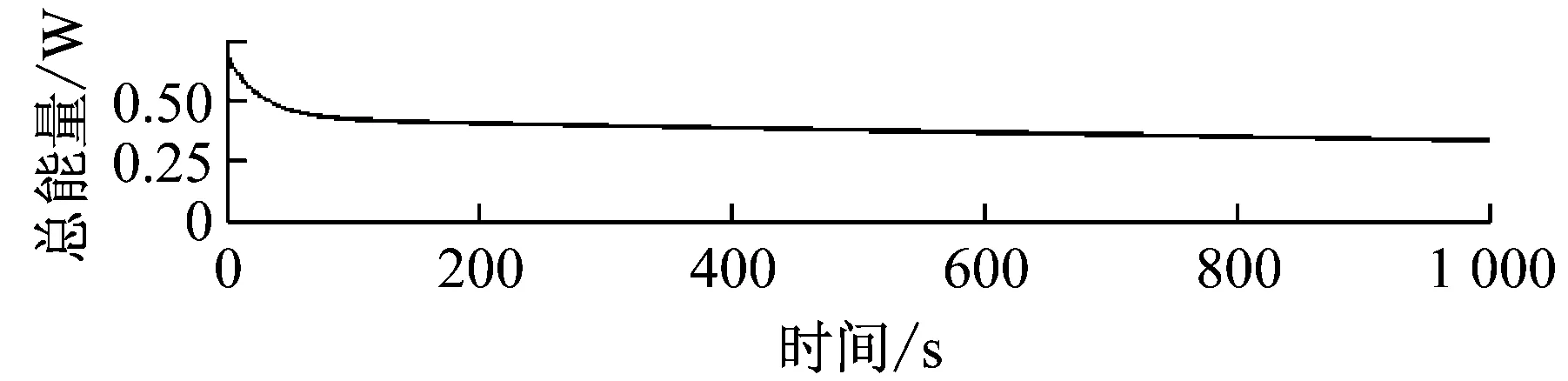
图5 参数失调时系统的响应曲线Fig.5 Response curves with parameter detuning

在图6所示的幅值谱曲线中，姿态运动在0.125 7 Hz位置出现了一个大小为0.761 4×10-3rad的峰值，而两个柔性附件在该频率位置处的峰值大小分别为0.486 5 m和0.390 2 m。

2.3 解耦与控制仿真分析

下面图7给出了2%的弯曲刚度失调率时，姿态运动和两个柔性附件广义位移的振动信号解耦误差结果，注意仿真中实际信号考虑为基于理论响应分析获得的理论解。很显然，基于最小二乘法的振动信号解耦方法非常有效。

图8给出了柔性附件2的弯曲刚度2%失调时，姿态运动响应的解耦控制效果与控制力矩信号。控制仿真中取反馈控制增益系数为-5 500，很显然加上控制力矩后，姿态运动的稳定性获得了显著增强，稳定阶段转角响应由控制前的2.541×10-3rad下降到0.505×10-3rad，控制效果达80.1%。图9给出了柔性附件2的弯曲刚度2%失调时解耦控制幅值谱效果，也可以发现控制系统中姿态响应中的第2、3阶频率信息(干扰信号)被有效地抑制了，转角幅值谱曲线在0.125 7 Hz处的峰值控制效果达95.0%。很显然，当前提出的基于振动信号解耦方法的姿态干扰信号抑制方法非常有效，且仅对调姿激励进行设计，无外加激励影响。

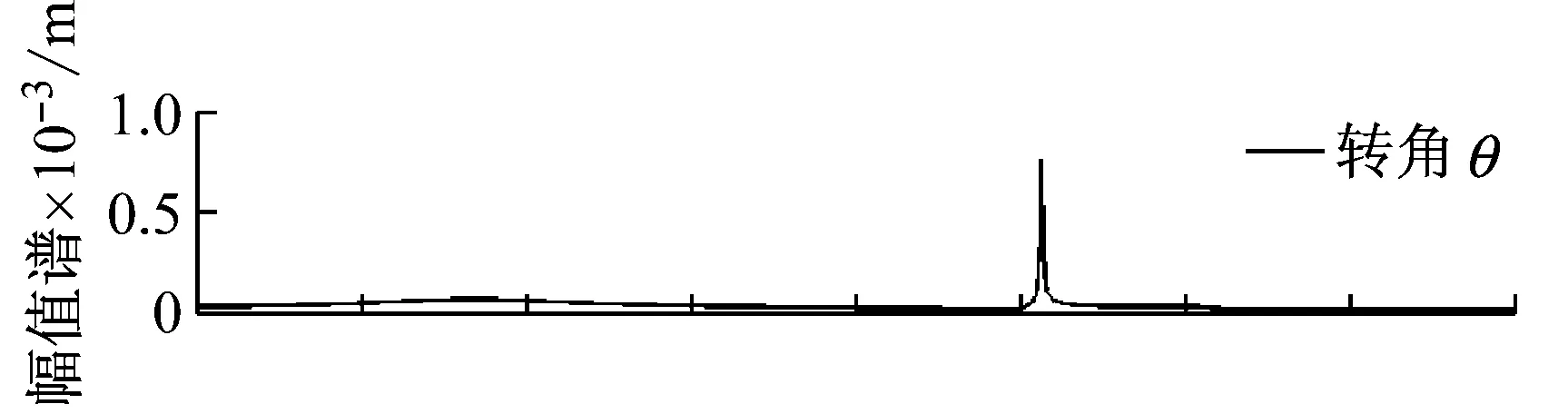
图6 参数失调时系统的响应幅值谱曲线Fig.6 Response spectrum curves with parameter detuning

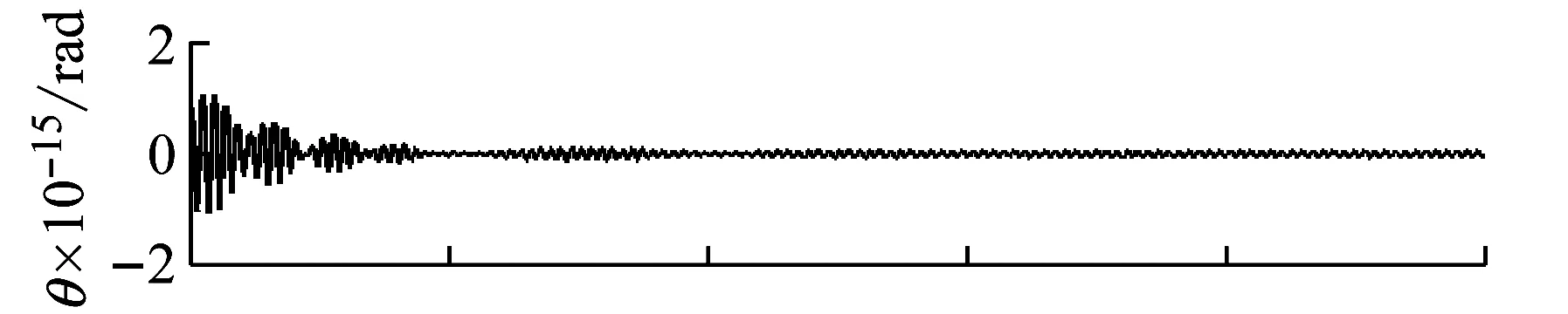
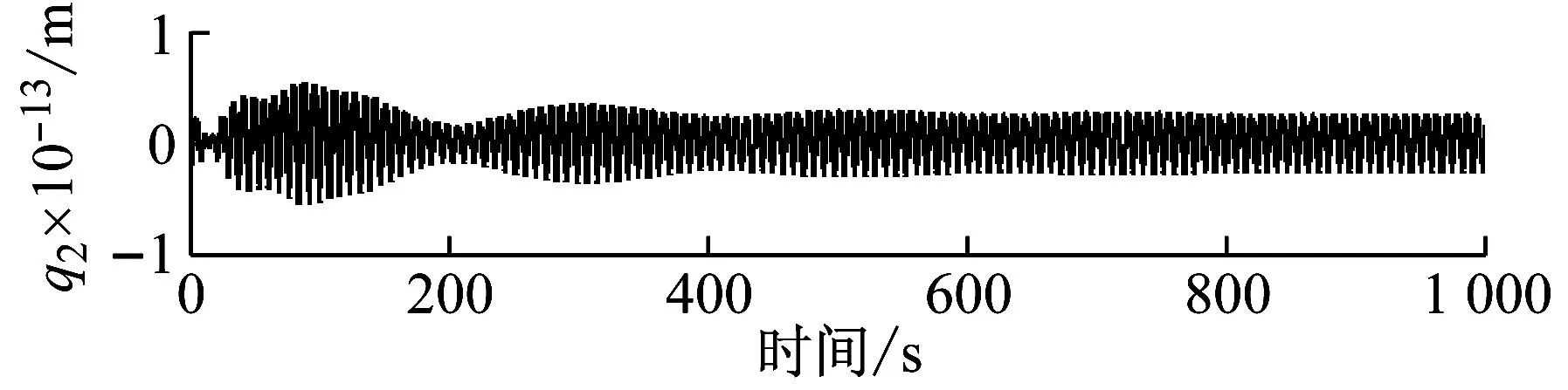
图7 柔性附件2的弯曲刚度2%失调时响应信号解耦误差

Fig.7 Decouple errors of response when bending stiffness of flexible appendage (2) is with 2% detuning

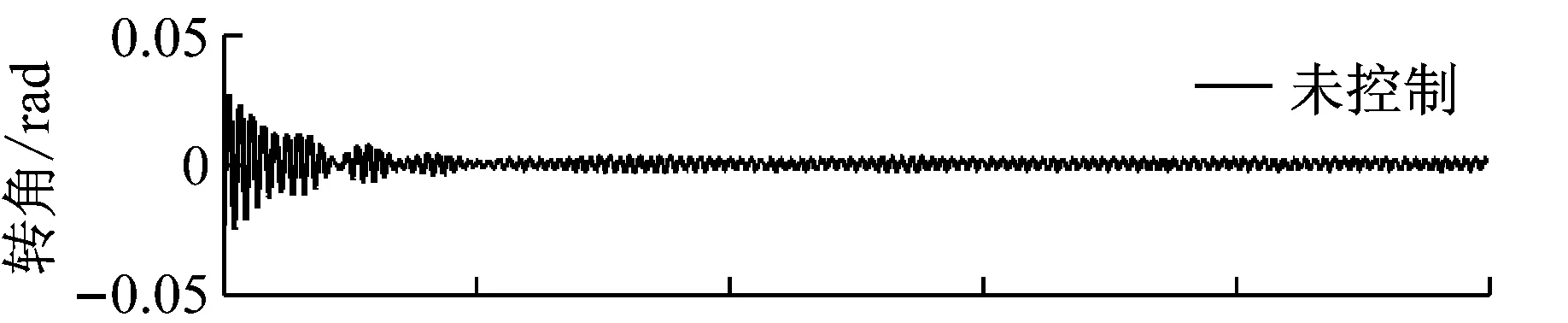
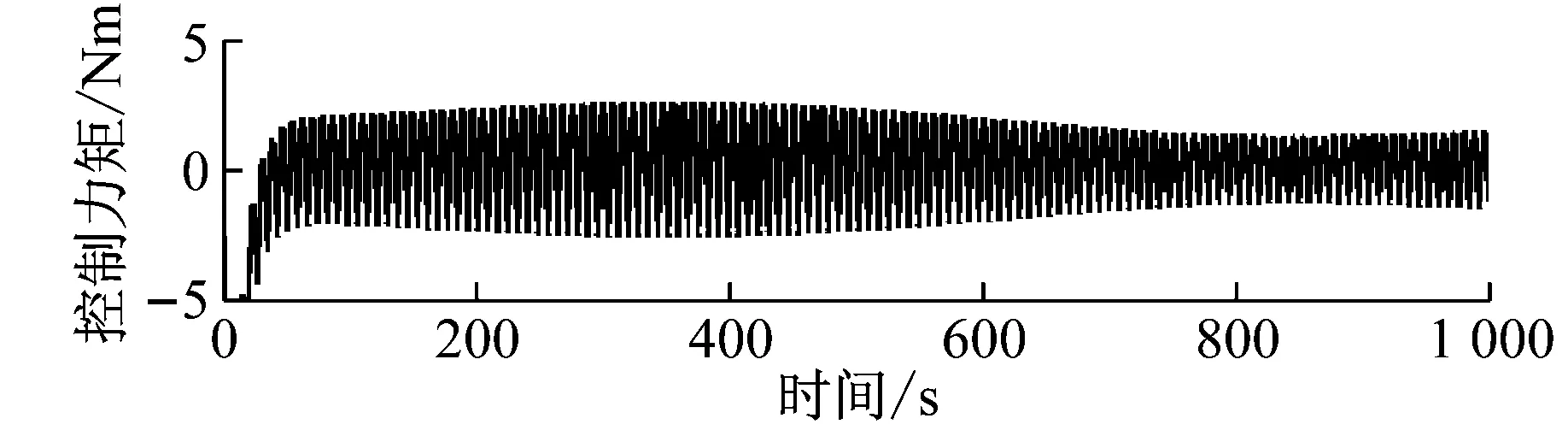
图8 参数失调时解耦控制效果与控制力矩信号

Fig.8 Control effect and control moment of decouple system with parameter detuning

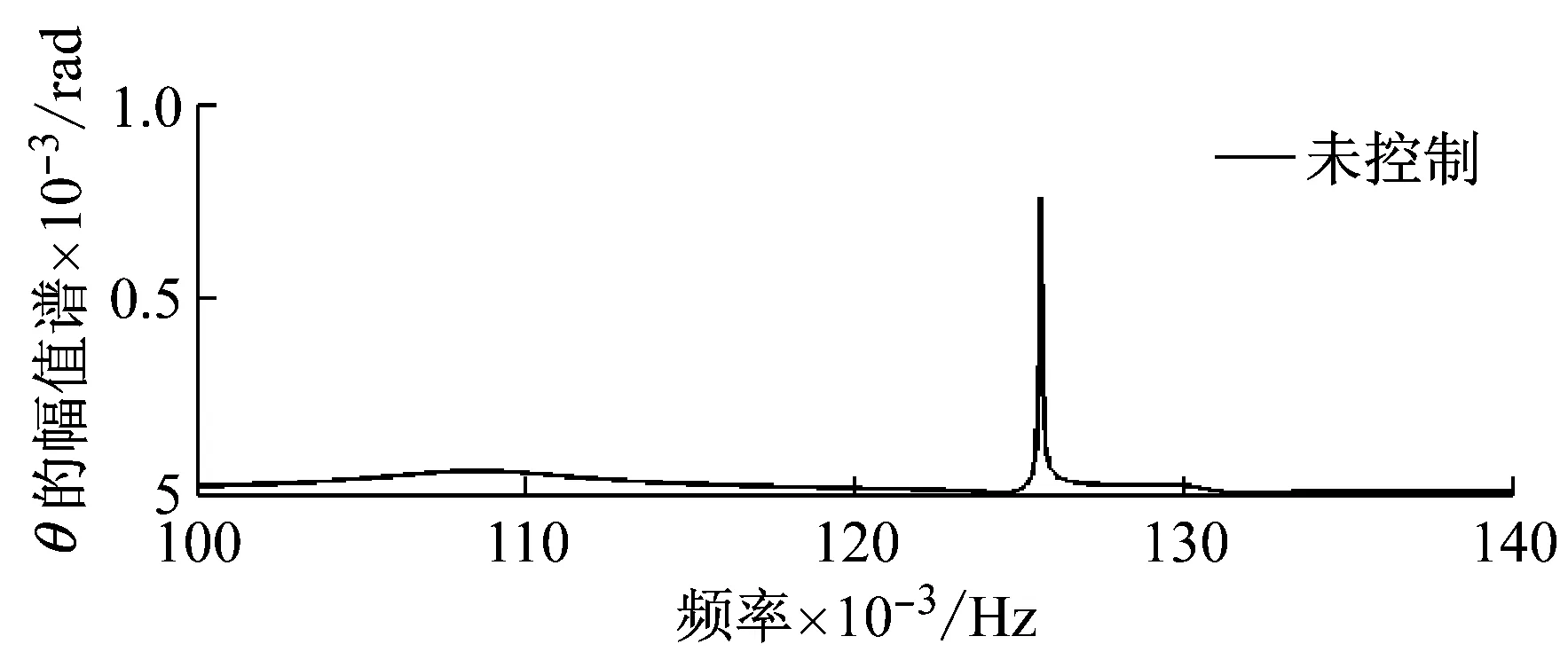
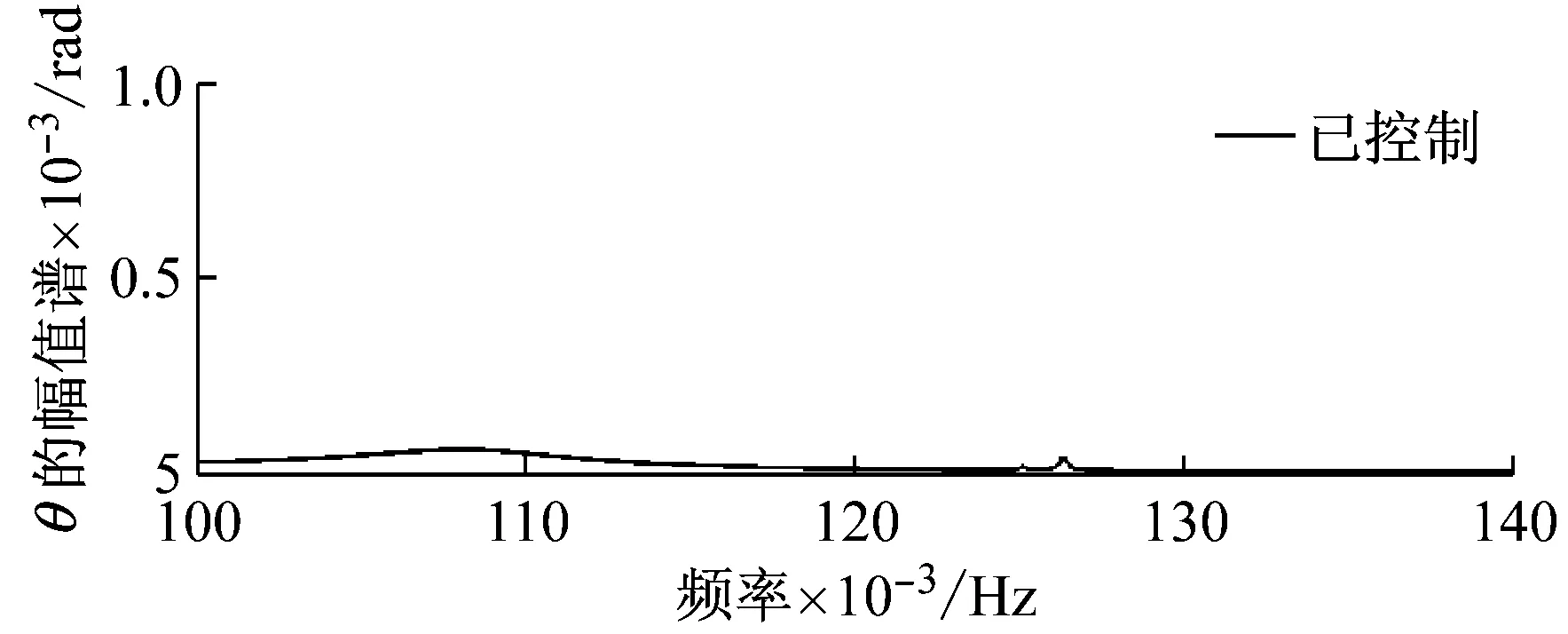
图9 参数失调时解耦控制幅值谱效果

Fig.9 Amplitude spectrums of non-control and control decouple system with parameter detuning

3 结 论

本文建立了典型柔性相似结构的动力学耦合模型，并开展了结构参数失调情况下的系统局部模态化研究。并进一步通过对系统的振动响应理论解形式的分析和基于最小二乘法，给出了耦合系统中振动响应信号的解耦方法，仿真发现该系统可实现高精度的信号解耦分析。同时，基于比例速度负反馈控制律设计，实现了参数失调时姿态运动响应的振动控制。

[1] 周舟，陆秋海，任革学，等．低密频太阳能帆板动力学参数在轨辨识和振动控制[J]．工程力学，2004，24(3)：84-89.

ZHOU Zhou, LU Qiuhai, REN Gexue, et al. On-orbit identification and vibration control for solar arrays with low and close frequencies[J]. Engineering Mechanics, 2004, 24(3): 84-89.

[2] 肖勇，王三民，陈国定．大型卫星天线系统固有模态的有限元分析[J]．机械设计与制造，2006(7)：1-2.

XIAO Yong, WANG Sanmin, CHEN Guoding. The modal analysis for satellite-large space antenna system with finite element method(FEM)[J]. Machinery Design & Manufacture, 2006(7): 1-2.

[3] BENDIKSEN O O. Mode localization phenomena in large space structures[J]. AIAA Journal, 1987, 25(9): 1241-1248.

[4] LEVINE WEST M B, SALAMAT M A. Mode localization experiments on a ribbed antenna[J]. AIAA Journal, 1993, 31(10): 1929-1937.

[5] 廖海涛，王帅，王建军，等. 失谐叶盘结构振动响应局部化实验研究[J]．振动与冲击，2012，31(1)：30-34.

LIAO Haitao, WANG Shuai, WANG Jianjun, et al. Tests for forced response localization of a mistuned bladed disk assembly[J]. Journal of Vibration and Shock, 2012, 31(1): 30-34.

[6] 杨智春，杨飞．T尾结构振动的模态局部化判据研究[J]. 力学学报，2010，42(2)：290-299．

YANG Zhichun, YANG Fei. Mode localization prediction criterion for t-tail structure[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(2): 290-299.

[7] 杨飞，杨智春．模态局部化对T尾颤振特性的影响[J]．振动与冲击，2010，29(8)：1-4．

YANG Fei, YANG Zhichun. Effects of mode localization on T-tail flutter characteristics[J]. Journal of Vibration and Shock, 2010, 29(8): 1-4.

[8] 苏继龙，陈敬焴．弱耦镜像对称工程结构模态局部化度结构参数表征[J]．振动与冲击，2012，31(7)：118-121．

SU Jilong, CHEN Jingyu. Characterization for mode localization level of weakly coupled mirroring symmetrical engineering structures with mistuned structural parameters[J]. Journal of Vibration and Shock, 2012，31(7)：118-121.

[9] 胡超，李凤明，邹经湘，等．失谐叶片-轮盘结构振动模态局部化问题的研究[J]．中国电机工程学报，2003，23(11)：190-194.

HU Chao, LI Fengming, ZOU Jingxiang, et al. A study on localization of vibration mode in mistuned bladed disk assemblims[J]. Proceedings of the CSEE, 2003, 23(11): 190-194.

[10] 李凤明，汪越胜，黄文虎，等．失谐周期结构中振动局部化问题的研究进展[J]．力学进展，2005，35(4)：498-512.

LI Fengming, WANG Yuesheng, HUANG Wenhu, et al. Advances of vibration localization in disordered periodic structures[J]. Advances In Mechanics, 2005, 35(4): 498-512.

[11] 倪振华. 振动力学[M]. 西安：西安交通大学出版社，1989.

[12] 刘相秋，王聪，邹振祝．考虑失谐的星载天线结构振动预测控制[J]．哈尔滨工程大学学报，2010，31(4)：434-437.

LIU Xiangqiu, WANG Cong, ZOU Zhenzhu. Predictive vibration control method for detuned satellite antenna structures[J]. Journal of Harbin Engineering University, 2010, 31(4): 434-437.

Vibrationcontrolofflexiblesimilarstructureswithdetunedparameters

LUO Yajun, XU Minglong, ZHANG Shuai, ZHANG Xinong

(State Key Lab for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049)

Coupled dynamic modeling and vibration control of flexible similar structures with detuned parameters are important for designing aerospace structures. The coupled dynamic model of a system was established with Lagrange method and its responses were decoupled based on the least square method. Furthermore, the active vibration control model was built and simulated to study the suppression of unstable responses of flexible similar structures with detuned parameters. Finally, the system modal localization caused by detuned parameters was simulated and analyzed. According to vibration control simulation results, it was indicated that the proposed active vibration control method for flexible similar structures with detuned parameters based on their decoupled responses is effective.

flexible similar structure; detuned parameters; modal localization; vibration control

国家自然科学基金项目(11572240)

2016-07-12 修改稿收到日期：2016-09-19

罗亚军 男，博士，讲师，1980年3月生

0327；V414.9

A

10.13465/j.cnki.jvs.2017.23.003