柔性多体系统含摩擦碰撞stick-slip过程动力学仿真

钱震杰， 章定国， 金诚谦

(1. 农业部南京农业机械化研究所，南京 210014； 2. 南京理工大学 理学院，南京 210094)

柔性多体系统含摩擦碰撞stick-slip过程动力学仿真

钱震杰1， 章定国2， 金诚谦1

(1. 农业部南京农业机械化研究所，南京 210014； 2. 南京理工大学 理学院，南京 210094)

基于高次刚柔耦合理论和Lagrange 乘子法，研究了柔性多体含摩擦碰撞stick-slip过程的全局动力学的精确建模与自动切换仿真问题。基于变拓扑思想，根据分离、碰撞、黏滞接触和滑动接触等状态分别构造相应的约束条件和动力学方程。运用冲量/动量法求解碰撞初始条件；引入切向滑动摩擦力势能的概念描述切向滑动接触力；给出接触、分离、黏滞、正向/逆向滑动状态之间的切换准则，实现了系统全局动力学自动切换。通过算例的数值仿真，分析了滑移/黏滞(微滑动)、正/逆向滑动等复杂非光滑现象，验证了该模型和算法的有效性。

含摩擦碰撞；黏滞/滑移；接触约束；柔性机械臂；动力学建模

柔性多体系统，如机械臂，操作过程存在着大量的抓取、分离、内外碰撞，末端执行器和操作控制较复杂。目前，工程应用上大量采用冲量/动量法和连续碰撞力法来近似求解多体系统的碰撞问题。Pfeiffer等[1]提出了附加约束法求解多体系统变结构问题。由于冲量动量法存在碰撞瞬时完成假设，无法求解接触力变化过程，而基于Herze理论的连续接触力法存在碰撞体互相嵌入假设，动力学响应依赖于接触模型参数选择。附加约束法[2-5]可得到碰撞过程接触力的变化、系统动力学响应，弥补前两者方法的不足。

一方面，该方法需要解决接触发生瞬时两界面间的速度跳跃的非光滑问题，并保证接触发生瞬时和分离之后碰撞力为零，否则可能出现接触和分离状态之间接触点速度和加速度的高频“假振荡”现象，或者数值不收敛。为此，Taylor等[6]基于Newmark积分格式的碰撞初始接触点速度和加速度的修正形式引入方程，得到稳定数值解。董富祥等[2]引入连续介质力学间断面理论来求解碰撞初始速度跳跃问题。另一方面，附加约束法等约束优化算法普遍存在由于数值积分误差累加造成的约束方程违约问题。目前主要有两大思路解决这一问题，即降阶转为常微分方程法和引入违约修正因子法[7-8]等。前者虽从根本上解决了违约问题，但降阶处理常伴随着新的数值求解精度问题；而后者数值收敛效果依赖于修正因子的选取。

含摩擦碰撞过程存在复杂的接触边界非光滑问题[9]，例如：接触面切向摩擦力与切向相对速度之间的非光滑性导致的黏滞-滑移现象、正/逆滑动方向转换与法向压缩/恢复切换不同步、以及摩擦微滑动等问题[10-11]。针对这些问题，Leine等[12]研究了多刚体系统中的冲击和摩擦的分支非线性问题。Payr等[13]研究了单杆与非弹性半空间碰撞接触中的黏-滑、正逆向滑动切换等非光滑问题。Zhao等[14]提出了满足边界条件的非线性弹簧阻尼模型和切向接触模型，考虑了碰撞过程中碰撞体之间的微运动，并分析了碰撞与结构柔性之间的耦合作用。姚文莉等[15]基于滑动模式步进算法研究了含铰摩擦的多刚体系统的碰撞动力学问题，考虑了切向模式的复杂性，解决了碰撞前后能量的不协调性。对于在柔性体中的含摩擦碰撞黏滞-滑移动力学建模和分析还有待进一步探索。

因此，本文运用附加约束法建立了柔性多体系统的含摩擦碰撞动力学模型。将系统分为非碰撞、碰撞初始接触、切向黏滞碰撞以及切向滑动碰撞四个状态，分别建立不同的动力学方程。碰撞初始条件采用冲量/动量法求解。根据黏滞/滑移切换条件判断，采用增减Lagrange乘子的附加约束法求解碰撞过程。并给出了仿真算例，分析了含摩擦碰撞的黏滞/滑移切换现象，验证了所提出模型和算法的有效性。

1 接触描述

在重力场下作回转运动的柔性机械臂上一点P与刚性碰撞面发生点-面斜碰撞，如图1所示。在柔性机械臂转轴O处建立描述大范围运动的惯性坐标系O-XY，碰撞面坐标系为O′-X′Y′，用浮动坐标系O-xy描述柔性梁的运动与变形。杆件的总长度为L，大范围运动转角为θ，FN和FT分别为法向、切向接触力。

图1 柔性机械臂碰撞示意图Fig.1 The flexible beam collision schematic diagram

令WP为惯性基到浮动基的转换矩阵[16]，hP为柔性机械臂运动变形后点P(xP,0)在浮动基中的位置矢量，表示如下：

(1)

式中：ux为轴向高阶耦合变形项；uy为横向弯曲变形项。令碰撞面单位外法向量和切向量分别为nP=[nx,ny]T，τP=[τx,τy]T。

令rQ为Q点在碰撞面中的位置矢量，WQ为惯性基到碰撞面坐标系的转换矩阵。经过推导归纳，得到碰撞法向间距矢量gN和切向间距矢量gT为

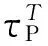
(2)

(3)

式中：Z(xP)为轴向高次耦合形函数矩阵；N为模态截断数；Φy为横向模态函数行阵；其中B(t)为横向模态坐标列阵。

2 系统全局动力学

2.1 系统碰撞初始条件的求解

(4)

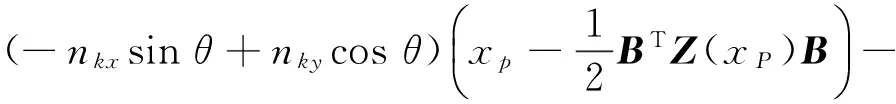
(nkxcosθ+nkysinθ)Φy(xP)B

(nkxsinθ-nkycosθ)φyi(xP)

(5)

同理，得到切向列阵dT=[dTθ,dTB1,…dTBN]T其中元素为

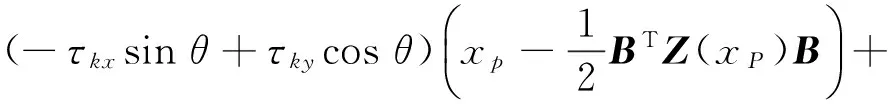
(-τkxcosθ-τkysinθ)Φy(xP)B

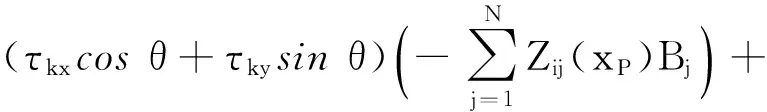
(-τkxsinθ+τkycosθ)φyi(xP)

(6)

(7)

2.2 系统切向黏滞动力学方程

若接触对发生黏滞，系统添加法向和切向接触约束，可得到系统碰撞黏滞阶段的微分-代数动力学方程为

(8)

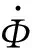
通过推到归纳，黏滞时法向位移约束Jacobi列阵Φz=[Φθ,ΦB1,…,ΦBN]中的元素为

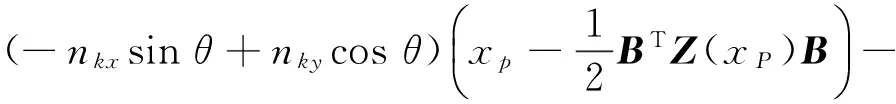
(nkxcosθ+nkysinθ)Φy(xP)B

(-nkxsinθ+nkycosθ)φyi(xP)

(9)

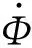
(10)

同理，通过推到归纳，黏滞时切向位移约束Jacobi列阵Γz=[Γθ,ΓB1,…,ΓBN]中的元素为

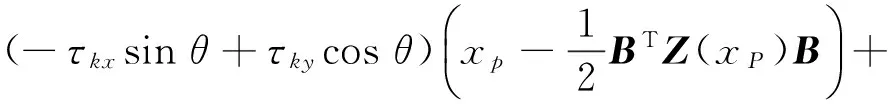
(-τkxcosθ-τkysinθ)Φy(xP)B

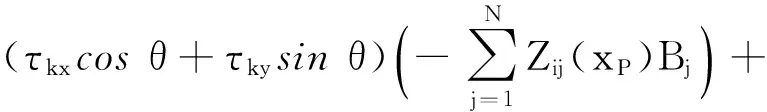
(-τkxsinθ+τkycosθ)φyi(xP)

(11)

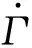
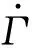
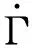
(12)

2.3 系统切向滑动动力学方程

若接触对切向滑动，法向约束依然存在，而切向约束解除。引入切向滑动摩擦力势能的概念VTs，根据库伦摩擦定律，VTs表达式如下：

(13)

(14)

2.4 黏滞/滑动状态切换准则

黏滞/滑移状态切换准则：连续接触状态存在黏滞、正滑移、逆滑移等现象，假设接触面材料各向同性、正/逆向摩擦因数相同μ，切向接触力为λT，则连续接触状态存在以下4种黏滞/滑动切换情况：

(15)

3 柔性机械臂与斜面含摩擦碰撞仿真算例

柔性梁与斜面发生碰撞，如图2所示。柔性梁密度ρ=2 766.7 kg/m3，弹性模量E=68.952 GPa，长度L=1.0 m，截面惯性矩I=7.85×10-9m4，截面积S=3.14×10-4m2。令初始无变形的梁从θ=0.125π位置在重力作用下自由下落，梁末端与面发生碰撞，碰撞点处切线为2x+3y=0，摩擦因数μ=0.3。仿真时间为2.0 s，无碰撞阶段的步长为1.0×10-4s，碰撞阶段的步长为1.0×10-6s，违约修正参数取α=20，β=20。

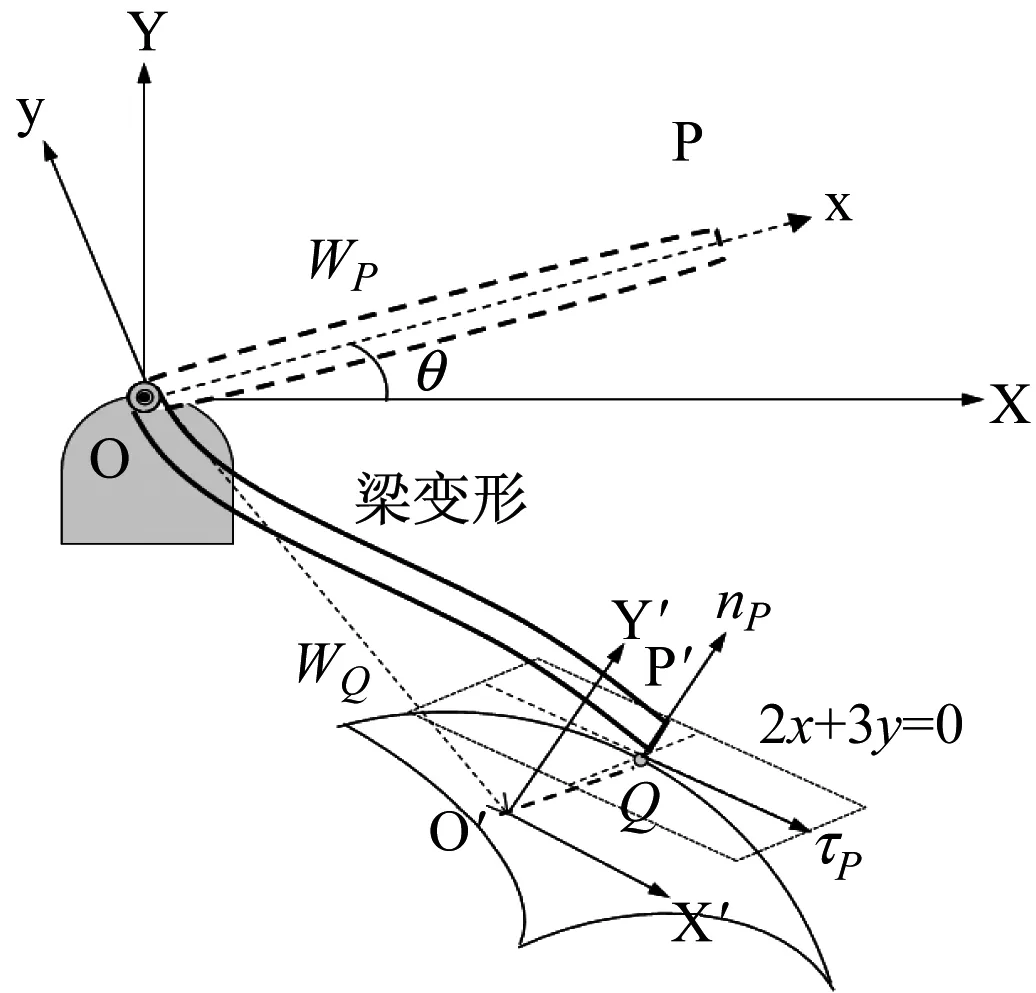
图2 斜碰撞示意图Fig.2 The schematic diagram of oblique collision

图3是柔性梁末端在基座坐标系中X横向和Y竖直位移。图4是整个仿真过程中系统的能量变化。由图可见：碰撞时能量损失较大；碰撞引发了柔性梁的高阶变形和高频振动，系统的弹性变形势能变化剧烈；碰撞结束后柔性梁向上反弹，动能又逐渐转化为势能，梁的机械能又保持恒定；多次碰撞后，重力势能逐渐降低至平衡位置为负值。

图5为2 s内法向碰撞力时程图。由仿真数据得：法向碰撞力首次高峰值发生在0.373 791 s，第二次高峰值碰撞发生在1.25 s附近，之间有多次小峰值碰撞。其原因是：碰撞发生后梁上靠近碰撞点的区域发生变形和振动，远端受到的碰撞影响较小仍维持原来的运动状态；随着时间的推移，碰撞动力学效应逐渐到达向关节端传播，并返回再传至碰撞点，造成第二次碰撞力峰值。由图可见：接近静止状态(t=1.36～1.37 s)时，碰撞引发柔性梁的弹性变形和高频振动，使得在一次接触中出现多次的次碰撞。

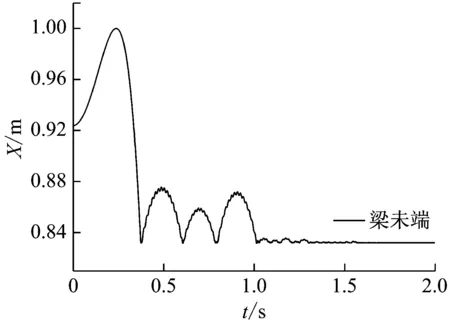
(a) 轴向位移

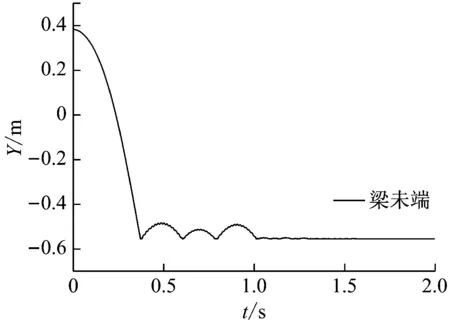
(b) 横向位移图3 梁末端位移Fig.3 The trajectory of link tip

图4 柔性梁的机械能变化Fig.4 Energy of the system

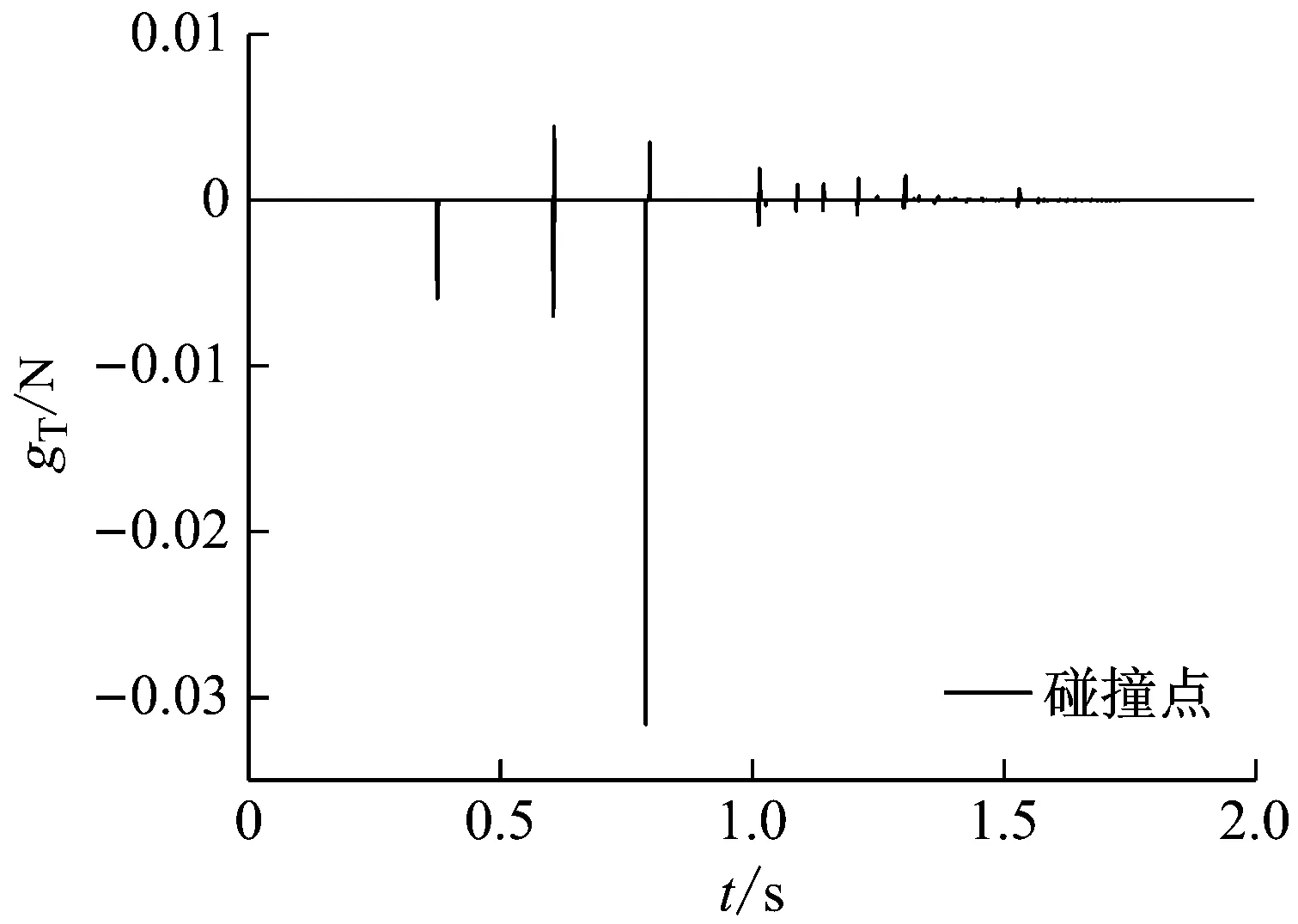
图6是切向碰撞力时程图。如图所示：首次切向碰撞力高峰值发生在0.373 791 s，第二次高峰值发生在1.375 s附近。同样，切向也存在碰撞力的两次高峰值不连续问题，而与法向碰撞力峰值的出现并不同步。接近系统静止状态(t=1.68～1.72 s)时，切向碰撞力的正负号变化颇为频繁，说明频繁发生正向滑动、逆向滑动、黏滞转滑动、滑动转黏滞等多样性接触状态切换。

图7为碰撞对的切向滑动位移。如仿真数据得到：碰撞发生后碰撞点的法向和切向相对速度振荡剧烈。与图6相对应的，切向滑动位移的正负号变化颇为频繁，存在多次正向/逆向滑动、黏滞转滑动、滑动转黏滞等状态的频繁切换。接近系统静止状态(t=1.30～1.38 s) 时，碰撞对的滑动位移在微小(黏滞)范围内反复振荡，直至静止。图8为碰撞对的相对速度切向绝对滑动速度：多次宏观碰撞、宏观碰撞中的次碰撞。如图所示，一次宏观的碰撞接触过程中，出现多次次碰撞接触。而切向接触在一次宏观接触过程中存在多次黏滞-滑动状态的频繁切换。

(a) t=0～2 s内

(b) t=1.36～1.37 s内图5 法向碰撞力Fig.5 The normal impact forces

(a) t=0～2 s内

(b) t=1.68～1.72 s内图6 切向碰撞力Fig.6 The tangential impact forces

(a) 滑动位移

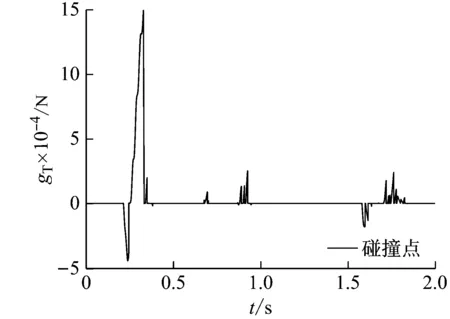
(b) 微滑动(黏滞)位移图7 碰撞点切向位移Fig.7 The tangential displacement of contact-pair

(a) 多次宏观碰撞

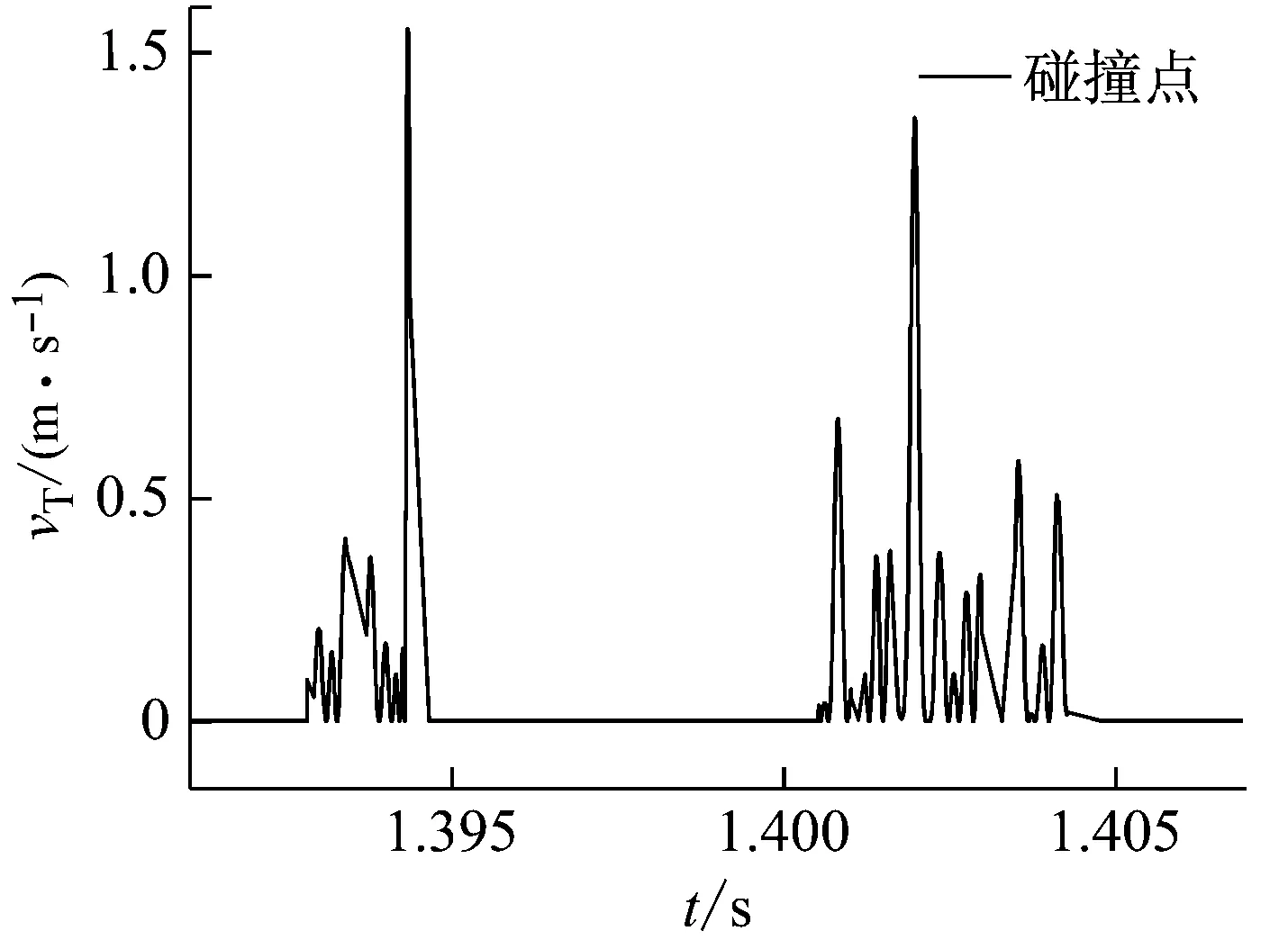
(b) 宏观碰撞中的次碰撞图8 切向绝对滑动速度Fig.8 The tangential slipping absolute velocity of contact-pair

4 结 论

针对柔性机械臂含摩擦碰撞黏滞-滑移过程，研究了系统变拓扑过程动力学的精确建模和自动切换问题。采用冲量-动量法求解碰撞初始时刻的速度跳跃，避免了速度不协调造成的反复脱开-接触的高频“假振荡”数值问题。引入切向滑动摩擦力势能的概念得到切向滑动约束方程。给出接触/分离、黏滞/滑切换准则，建立不同约束条件的动力学方程，解决了碰撞初始速度跳跃和切向摩擦引起的数值不稳定和能量不一致问题。通过仿真算例，分析了黏滞/滑移、正/逆向滑动等复杂切换现象，分析了柔性变形与碰撞的耦合效应，验证了本文提出的模型和算法的有效性。

[1] PFEIFFER F, FOERG M, ULBRICH H. Numerical aspects of non-smooth multibody dynamics[J]. Computer Methods in Applied Mechanics & Engineering, 2006, 195(50/51): 6891-6908.

[2] 董富祥, 洪嘉振. 平面柔性多体系统正碰撞动力学建模理论研究[J]. 计算力学学报, 2010, 27(6): 1042-1048.

DONG Fuxiang, HONG Jiazhen. Study on the modeling theory of the normal impact dynamics for the planar flexible multibody system[J]. Chinese Journal of Computational Mechanics, 2010, 27(6):1042-1048.

[3] 段玥晨, 章定国, 洪嘉振. 作大范围运动柔性梁的一种碰撞动力学求解方法[J]. 机械工程学报, 2012, 48(19):95-102.

DUAN Yuechen, ZHANG Dingguo, HONG Jiazhen. Method for solving the impact problem of a flexible beam with large overall motion[J]. Journal of Mechanical Engineering, 2012, 48(19):95-102.

[4] 王检耀, 洪嘉振, 刘铸永. 接触碰撞动力学的多变量选取方法[J]. 力学学报, 2014, 46(2):318-322.

WANG Jianyao, HONG Jiazhen, LIU Zhuyong. Multi-variable selection method in contact/impact dynamics[J]. Acta Mechanica Sinica, 2014, 46(2):318-322.

[5] QI Z H, LUO X M, HUANG Z H. Frictional contact analysis of spatial prismatic joints in multibody systems[J]. Multibody System Dynamics, 2011, 26(4):441-468.

[6] TAYLOR R L, PAPADOPOULOS P. On a finite element method for dynamic contact/impact problems[J]. International Journal for Numerical Methods in Engineering, 1993, 36(12): 2123-2140.

[7] FLORES P, MACHADO M, SEABRA E, et al. A parametric study on the Baumgarte stabilization method for forward dynamics of constrained multibody systems[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(1): 011019.

[8] 付士慧, 王琪. 多体系统动力学方程违约修正的数值计算方法[J]. 计算力学学报, 2007, 24(1):44-49.

FU Shihui, WANG Qi. A numerical method for constraint stabilization of dynamic equations of multi-body systems[J]. Chinese Journal of Computational Mechanics, 2007, 24(1):44-49.

[9] 金栋平, 胡海岩. 碰撞振动及其典型现象[J]. 力学进展,1999,29(2):155-163.

JIN Dongping, HU Haiyan. Vibro-impacts and their typical behaviors of mechanical systems[J]. Advances in Mechanics, 1999, 29(2):155-163.

[10] 王琪, 庄方方, 郭易圆, 等. 非光滑多体系统动力学数值算法的研究进展[J]. 力学进展, 2013, 43(1): 101-111.

WANG Qi, ZHUANG Fangfang, GUO Yiyuan, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems[J]. Advances in Mechanics, 2013, 43(1):101-111.

[11] 丁千, 翟红梅. 机械系统摩擦动力学研究进展[J].力学进展, 2013, 43(1): 112-131.

DING Qian, ZHAI Hongmei. The advance in researches of friction dynamics in mechanics system[J]. Advances in Mechanics, 2013, 43(1):112-131.

[12] LEINE R I, CAMPEN D H V, GLOCKER C H. Nonlinear dynamics and modeling of various wooden toys with impact and friction[J]. Journal of Vibration & Control, 2003, 9(1/2):25-78.

[13] PAYR M, GLOCKER C. Oblique frictional impact of a bar: analysis and comparison of different impact laws[J]. Nonlinear Dynamics, 2005, 41(4):361-383.

[14] ZHAO Z, LIU C S. The analysis and simulation for three-dimensional impact with friction[J]. Multibody System Dynamics, 2007, 18(4):511-530.

[15] 姚文莉, 陈滨, 刘才山,等. 含摩擦的多刚体系统碰撞问题的滑动状态步进法[J]. 应用数学和力学, 2007, 28(12):1448-1454.

YAO Wenli, CHEN Bin, LIU Caishan, et al. Sliding state stepping algorithm for solving impact problems of multi-rigid-body system with joint friction[J]. Applied Mathematics & Mechanics, 2007, 28(12):1448-1454.

[16] 吴胜宝, 章定国. 大范围运动刚体-柔性梁刚柔耦合动力学分析[J]. 振动工程学报, 2011, 24(1): 1-7.

WU Shengbao, ZHANG Dingguo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion[J]. Journal of Vibration Engineering, 2011, 24(1):1-7.

Dynamicsimulationforflexiblemultibodysystemscontainingfrictionalimpactandstick-slipprocesses

QIAN Zhenjie1, ZHANG Dingguo2, JIN Chengqian1

(1. Nanjing Research Institute of Agricultural Mechanization of National Ministry of Agriculture, Nanjing 210014, China；2. School of Sciences, Nanjing University of Science and Technology, Nanjing 210094, China)

The dynamic simulation including modeling and automatic switching for flexible multibody systems was investigated using Lagrange multiplier method and the high order rigid-flexible coupled theory. Based on variable topology idea, dynamic equations and the corresponding constraint conditions were established, respectively for detachment, impact, viscous contact and slip contact states. The impulse-momentum method was used to solve the impact initial conditions. The concept of tangential sliding friction force potential energy was introduced to describe the corresponding generalized impact forces with Lagrange equations. The switching criteria among contact, detachment, stick and slip were built to realize the global dynamic automatic switching of the system. Examples were numerically simulated to analyze the complex non-smooth phenomena including forward/backward slip and slip/stick(micro slip) to verify the effectiveness of the proposed model and algorithms.

frictional impact; stick-slip; contact constraints; flexible robot arm; dynamic modeling

国家自然科学基金青年科学基金(11602120)；国家自然科学基金(11272155;11132007)；国家科技支撑计划(2013BAD08B02)

2016-07-13 修改稿收到日期：2016-09-24

钱震杰 女，博士，助理研究员，1985年生

金诚谦 男，博士，研究员，1973年生

O313；O322

A

10.13465/j.cnki.jvs.2017.23.006