条件概率应用的误区

谢美华

(湖南涉外经济学院管理学院 410073)

1 引言

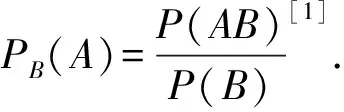
然而在实际应用中，该公式却经常没有得到正确应用，比较经典的问题是“生孩子”问题.问题为：一个家庭有两个孩子，已知一个是男孩，另一个是女孩的概率是多少？争议很大的答案有两个，分别为1/2和2/3.天涯论坛上连续有几个关于此问题的发帖[2-3]，从发帖上广大网友的留言来看，支持者各占一半.

综合网友的发言，发现认定答案为1/2的人的主要看法有以下几种：

第一种：你第一胎生男生女，不会影响第二胎，第二次生女孩依然是二分之一，二者是独立的.

第二种：一个是男孩另一个是女孩的情况有两种，一是姐弟，概率为1/2乘以1/2等于1/4；二是兄妹，概率同为1/4.将两种情况相加得1/2.

第三种：两个孩子的家庭，共有男女、男男和女女这三种情况，已知一个孩子是男孩，因此去掉女女的情况，还剩下男女和男男两种情况，因此另一个为女孩的概率为1/2.

这三种想法都没有真正理解题意，主要表现为对条件的把握和利用方式不对，对增加条件后的样本空间缺乏认识.这也正是条件概率学习中经常碰到的问题.

与此相似的问题还有三门问题[4].

2 条件概率的误区

误区一：对条件概率中的条件把握不准确，致使条件事件的定义不准确

生孩子问题中的条件是“一个家庭有两个孩子，已知一个是男孩”，从题意不难理解这里“一个为男孩”的含义是至少有一个是男孩，并不是“一个家庭有两个孩子，已知老大是男孩”，或者“一个家庭有两个孩子，已知老二是男孩”.如果错误地理解为后面两种情况，则会得到1/2的结果.

下面对这三种情况，分别给出其条件概率的计算结果.

问题一：一个家庭有两个孩子，已知第一个是男孩，求另一个是女孩的概率？

解：设事件A表示第一个为男孩，事件B表示第二个为女孩，显然这两个事件是独立的，因而PA(B)=1/2.

问题二：一个家庭有两个孩子，已知第二个是男孩，求另一个是女孩的概率？

解：与问题一相同，定义设事件A表示第一个为女孩，事件B表示第二个为男孩，则PB(A)=1/2.

问题三：一个家庭有两个孩子，已知其中一个是男孩，求另一个是女孩的概率？

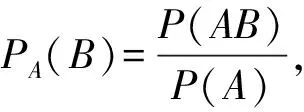
如果不理解清楚条件的含义，错误地定义事件A、B就会出现问题一和问题二的结果，上节中持有第一种错误观点的人就是这种错法.

误区二：对增加条件后样本空间的变化没有理解

前文所述的第二种错法就是属于忽视了条件，对增加条件后样本空间的变化缺乏分析.既然条件已说明至少一个是男孩，则排除了女女的情况，因而加了条件的样本空间中就只剩下男女、女男和男男三种情况，显然另一个为女的概率是2/3.这种错法中，实际上是认为此时的样本空间仍然为男男、男女、女男、女女，因此得到的概率仍然为1/2.

误区三：在概率计算中出现错误

针对上文的问题三，有不少同学会出现概率计算错误.例如，有同学会将上文中“至少有一个男孩的概率”P(A)计算为2/3，理由是两个孩子的情况分别是男男、女女和男女，因此有男孩的概率是2/3，这一部分同学在计算P(AB)同样也容易算成1/3，因而也会得到PA(B)=1/2.这属于对样本空间理解不清，实际上此处样本空间应为男男、女女、男女、女男.前文所述的持有第三种错误观点的同学就是这种错法.

3 解决方法

1)结合题目的背景，正确理解条件

对于条件概率问题，首先一定要理解清楚条件，否则就容易犯第一种错误.当然对于条件的理解有时和题目背景交待不清楚有关，因此大家应结合问题提出的实际背景来考虑.

2)正确定义增加条件后的样本空间.条件概率PA(B)中新的样本空间实际上已经缩减为事件A，而不再是原来的样本空间Ω.

3)把握好概率计算的每个环节.概率的计算是计算条件概率的基础，在对条件概率中分子分母的概率进行计算时，一定要准确把握事件和样本空间，这样才不会出现概率计算错误.