初中数学诊断性考试评价的探索

周先荣

(江苏苏州木渎实验中学 215000)

目前，很多初中的数学诊断性考试评价名目繁多，有期初考、期中考、期末考、月考、单元考等等，且评价内容过多倚重学科知识，评价标准过份强调共性，评价方法一张试卷.为此，本文通过PISA与中考数学的对比[1]，就初中数学纸笔诊断性考试评价(简称诊断考试)的内容、方式进行了肤浅的探索.不足之处，请方家指教！

1 他山之石，PISA和中考的对比与借鉴

PISA(国际学生评估项目)是由OECD(经济合作与发展组织)统筹的学生能力的国际评价计划，是一项以改善教育政策为导向的跨国测评研究项目.为了便于比较，我们选择苏州2012中考数学试题(120分钟，29个题，选择题分值占23.07%)和PISA2012数学测试题(60分钟，26个题，选择题占50.00%)，在主题内容和认知要求两个维度进行对比分析.主题内容分为数感、运算、测量、消费者应用、基础代数、几何概念、数据展示、统计、概率、分析、三角几何、函数和教学基础；认知要求分为回忆、执行程序、展示理解、推测/概括/证明、解决非常规问题/建立联系.其中，差距比较大(超过3%)的几项见表1、表2.

表1 PISA2012和苏州市2012中考数学主题内容差距较大的分布

表2 PISA2012和苏州市2012中考数学认知要求差距较大的分布

两份试卷的一致性指数仅为0.46，说明存在很大差异.主题内容方面，测量、数据展示、统计这几项我们的测试比重相对较少，几何三角、函数方面测试比重相对较大；在认知要求方面，存在较大差异，其中“问题情景”差异惊人.

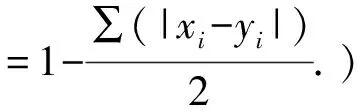
2 丰富内容，文化整合与情景开放交融

目前，存在一种不正常的现象，就是初中各级考试的内容都瞄准中考，甚至照搬中考题.中考是选拔考试，是对三年学习的终结性测量与评价.而平时的考试更多是阶段性的诊断考试，特别是初一、初二的诊断考试，其更重要的功能是形成较为准确的教育判断，以利改进教师教学和管理，促进学生学习.诊断考试内容过分局限于考察学生的式感、空间观念、计算能力、思维能力与推理能力等核心问题，削弱了考试的调节、导向、激励、育人功能是不可取的.因此，平时诊断考试应该关注学生的发展性和核心素养，在重视数学的生活性、情景性和过程性以外，还突出个体对数学的认识和态度的评价.诸如数学史、数学文化、数学审美、数学应用等体现个人数学修为的内容，在平时诊断考试中应更加丰富.

2.1 渗透数学史，接受优秀数学文化的熏陶

现代数学教育，是将数学置于人类文化大背景下对其进行哲学的反思，它是人类文化的重要组成部分，对人类智力、美学和道德方面有着培养的功能.数学文化已经超越了专业研究范畴，广泛进入基础教育，也就有了迫切的诊断考试要求，高考也明确提出要增加数学文化的考试内容.如何把数学文化转化为诊断考试形态，以下几个方面值得关注.

2.1.1数学典籍为背景，让考题助力数学史的传承

初中数学考试的命题在重视考查学生运用观察、分析、计算、计划、方法、思维，综合运用所学知识与技能解决问题的能力的同时，有责任渗透性考察学生数学文化方面的认识，提醒学生在社会文化的大背景下，去看待数学和理解数学，领略数学审美，透过数学的规则体会理智与自律，经历数学的严谨学会敬业与求真，通过科学与人文相济，发展数学教育应有的育人功能，这其中数学典籍的作用尤为重要.如，在检测解二元一次方程时，为了了解二元一次方程的几何解法，了解古人的“代数几何”思想，我们设计了这样的考题.

命题1在欧几里得的《几何原本》中记录了很多“数形结合”的经典问题.在第二卷中的命题11中记录了方程ax+x2=a2的几何解法.如图,作边长为a的正方形ABCD,E是线段DA中点，以E为圆心，EB为半径画圆，与DA的延长线交于F点，作正方形AFGH，延长GH交于DC于K.“我们将把一个与给定的正方形ABCD(面积)相等的矩形DFGK(一边)置于线段AD上，并多出一个正方形AFGH”.这样，AF的长的数值就是方程x2+ax-a2=0的一个解.请你参考上述方法，给出方程x2+2x-4=0的正数解(近似值)是.

本题旨在不通过求根公式，而是借助画图通过测量手段来解方程.考后，很多学生在谈论《几何原本》，谈论为什么要“面积相等”等等.事实上，考试不是让学生机械答题，更重要的作用是引起学生自发的谈论数学.引起学生了解数学史料，增强考后阅读数学典籍内容的意识.

2.1.2数学名题为背景，彰显古代名题的现代教育价值.

如果说数学文化是浩瀚的宇宙，那么数学名题就是闪烁的星星.数学名题都是历史的积淀，在当时的历史条件下名噪一时，也给数学打上了浓厚的文化烙印.事实上，一个好的问题可能改变一个人的人生轨迹.如：欧拉(Euler)受“哥尼斯堡七桥问题”的启发发明了“图论”；泊松(Poisson)因为对“三个瓶子分啤酒”问题的研究而痴迷于数学，成为一代数学大师.有些历史名题与课程目标密切相关，打开尘封已久的记忆，重现这些问题的现代数学价值，实际上是揭示数学科学中的人文精神，使学生得到优秀文化的熏陶，更是提高学习兴趣的源泉.如，考察一元一次方程应用的时候，我们就挪移了古代的问题设计了这样的考题.

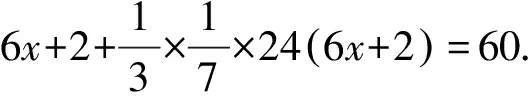
类似这样的问题在《九章算术》中有很多，《九章算术》是数学家向帝王提出如何“丈量田亩、征取税金、摊派徭役、计算土方”等实用数学问题的总结，其中的一些问题到现在依然具有生命力.这些问题的重现，重在引发数学思考，在对问题进行提炼和加工的过程中，生成学生的自主探究、自主发现，揭示问题背后的数学本质、思想.让古老的实用问题交融于现代的数学学习，使思维更加理性，这也是我们应有的教育行为.

2.1.3 趣味数学为背景，让考题怡情怡性.

生活中流传着许多脍炙人口的趣味数学故事.如：中国古代的“鸡兔同笼”、“九宫图”等，都是孩子喜欢钻研的，对学生的激励价值是不言而喻的.现代生活中，也有许多学生喜欢的趣味数学故事，有些是非常好的考试情景.通过数学趣味题，可以欣赏数学之美，享受数学之趣，领略数学的魅力.如初一上学期的期中考试，我们设计了这样的考题.

命题3一百零八塔是中国现存的大型古塔群之一，位于银川市南60公里的青铜峡水库西岸崖壁下，塔群坐西面东，依山临水.佛塔依山势自上而下，按1、3、3、5、5、7、9、11、13、15、17、19的奇数排列成十二行，总计108座，形成总体平面呈三角形的巨大塔群.现要求重新设计一座塔，使塔的总数是133个，共13行，每行塔数为奇数且只允许两行中的塔数重复(如题中已有的3，3，5，5)，则各行的塔数从小到大依次为(重复的塔数一起写出，设计一种即可).

有人认为此题与当时学段的学习联系不密切，其实不然，它延续了小学的“数感”，对初中学生的直观、分析、猜想要求很高，学生也非常感兴趣.问题也与佛学的知识相连,有一定文化相通的气息，对学生的精神追求，提高“数学情商”很有意义.

2.2 加强学科联系，提高跨界整合能力

现代课程知识“交汇”非常频繁，要在不同知识体系的交汇处适当加强检测，逐步提高学生对知识“整合”的意识.通常情况下，课本上不同的知识体系间往往蕴涵着某些本质的联系，只要注意引导，学生完全可以利用自己的力量把这种关系揭示出来.特别的，引导学生在不同学科的交汇处发现问题，实际上是培养学生对不同学科的跨界“相互利用”能力，这种高层次的学科融合、学科渗透正越来越受到人们的关注.如，提起对称性，多数学生首先反应出的是几何图形的对称，其实对称存在于每个学科和生活的每个角落，为了引领学生欣赏这种对称美，我们设计了这样的考题.

命题4下列四个选项中，有的句子、单词字母具有对称规律.其中没有这种规律的一项是( )

A．清水池里池水清 B．有志者事竞成

C．上海自来水来自海上 D． level

D选项仿照A、C选项，是以语文中的“回文句”为背景，这种题加深理解生活中的轴对称现象，题目新颖，妙趣横生.

2.3 构建适切情景，培养学生生活中发现数学的意识

考题情景是指为考题特别设定的某个具体(生活)问题，在问题解决的过程中显化数学能力，阅读理解能力、数学表述能力、推理和论证能力、制定解决问题策略的能力、使用符号化、公式化、技术性语言和运算能力以及使用数学工具的能力等.依据主要是荷兰著名数学家和教育家费赖登塔尔(H.Freudenthal)的“数学来源于现实，且寓于现实中.”考题情境的构建要能够在问题的解决过程中掌握“数学化”的方法.并寻找数学知识在客观世界中的实际背景材料，把大量的数学好题置于学生所热爱的生活情境之中，让学生亲身体验数学的实际创造过程，从而提高学生从生活中发现数学的意识.

从统计看，我们中考17.70%的考题有情景，而PISA测试的所有问题都有情景.应该说，PISA考题情景的构建形式和内容对我们有很大的启发和借鉴作用，在此不再例赘举.笔者认为考题情景的构建应关注以下几个方面：①关联性.首先，问题的本身要有一定的数学内涵，体现出一定的数学价值.其次，问题要有针对性，与考查的目标有“鱼与水”的关联，很容易切中考试目标、切中问题的要害；②趣味性.情景符合学生的心理特点，引起学生的兴趣，关键是考后还能引起学生谈论数学的激情；③可及性.生活经验和情景之间要紧密联系，由情景到问题解决的思维“维度”不能太大，要有“台阶”，让学生“跳起来摘桃子”；④时代性.情景贴近时代生活，及时从身边的媒体、新闻事件及学生生活体验中发现情景价值，保持情景的新颖性，甚至可以从国家发展的热点问题构建情景，增加学生爱国热情.

2.4 增加问题开放性，提升学生发现问题的意识

诊断考试要想让学生从生搬硬套上升到灵活思考，需要尽量规避一些一看就知道是“做过了”的记忆性问题.为达到这个目的，除了增加问题的情景外，还可增加问题的开放性，减少一问一答机械命题模式.比如，本文的命题3，结果不唯一具有探索性，是较为开放的问题.有时，可以给出考题条件让学生创设问题结果，也可以给出问题的结果让学生补充条件等等，让问题更加开放.

命题5如图，ABCD中，E、F是对角线AC上的两个点，请你适当添加一些条件，并依据这些条件提出一个正确的结论.

添加的条件：

正确的结论：

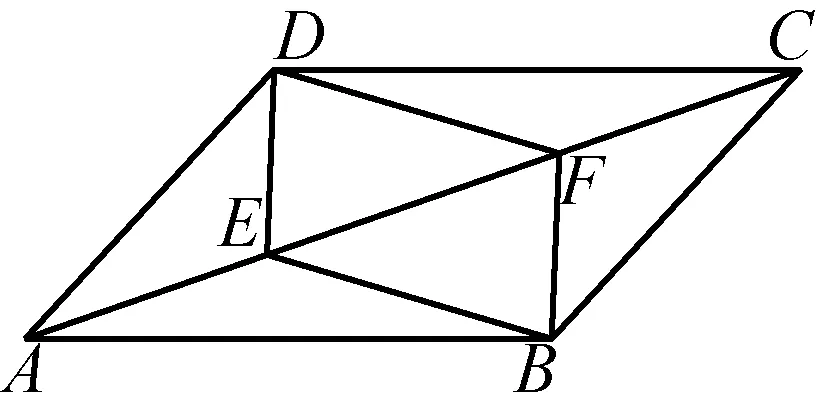
有些重要图形是研究很多问题的载体，要加大学生对这些图形的探究力度.本题中的图形，教材中多次出现并加以变化形成了相应的问题链条.编拟此题的目的，就是让学生依托这个基本图形去提出问题，“提出一个问题往往比解决一个问题更重要.因为解决问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，却需要有创造性的想象力，而且标志着科学的真正进步.”(爱因斯坦).考试的对象是学生、是人，是活生生的个体，考题不应该都是唯一呆板的答案和机械的完成答卷，也应该是火热的创造过程.不在于学生答案的标准化，而在于学生能够给出自己的想法，以激发学生的创新思维.对于开放性试题的评分不应有很硬性的评分标准，只要符合要求，具有一定的综合水平就行.在量分的过程中，教师要以公正、宽容和发展的眼光看待学生的“作品”，将有独特创意的答案给以高分.

3 形式多样，自主命题与分层检测并举

为了终结性评价向过程性评价和发展性评价转变，实现学生“指向目标达成的自我学习力的提升”.可以运用多样的资料，诸如教学过程中产生出的学习卡片、作业、作品、表演、录音、录像、考试等资料与信息，多角度、综合地评价学生，求得教学与评价的一体化.但在目前的环境下，这些评价如何操作还有待深入的研究.就现有纸笔考试而言，我们不必寻求对其进行颠覆性变革，适当配合口头考试评价、操作考试评价、开放考试评价、合作考试评价、自主考试评价、分层考试评价等形式，在命题内容、命题形式、命题人上都可以进行新的探索.

3.1 “我的学习，我来考”，学生命题很出色

布卢姆(Benjamin Bloom)把认知领域的目标分为六个领域：知识、领会、运用、分析、综合和评价.其最高层次是学生能够评价自己的学习，针对学生如何才能自主评价，我们进行了尝试.

第一种方式：自主命题，学生做自己的主考官.千年来，都是“主考官”考学生，学生能不能自己命题考自己呢？我们尝试不再由老师命题考学生，而是让学生自己考自己.首先，每个学生自主命题各自出一份试卷，交给老师审核并统一保管.然后，在统一的时间，在无人监考的情况下，同位同学相互考对方出的试卷，或小组内部采用“推磨式”考法，A考B出的试卷，B考C出的试卷……F考A出的试卷，考后分别交给命题的同学批改.

第二种方式：合作命题，小组互考也精彩.将班级分成若干学习小组，组间同质组内异质，小组之间随机结对互考.每个小组内部合作命题出一份试卷，在统一的时间考试，分别考另一个小组出的试卷，考后试卷按小组收齐，交由命题小组的小组长集中批改.

这两种考试形式的目的是让学生自主命题，增加自主评价的能力，其关键是学生能够出好一份试卷.为此，老师要做好以下工作：

其一，命题形式规范.首先，要做好学生和家长的动员工作，讲清考试“分数”和自我定位、自我评价、自我认知的关系，让学生从个人成长的高度来出好试卷.其次，做好学生命题的培训工作，通过剖析试卷范例，对考试时间、内容、题目数量、难度、梯度等，让学生知道如何把握这些要素，逐步培养学生能出一份高质量的试卷.

其二，命题内容适切.题目的难易要符合命题人自己的学情，懂得如何选择考题，如何进行题型的搭配，鼓励学生拓展、改编、编拟问题.

其三，适当寻求帮助.命题过程中出现困难，比如画图操作等，可以寻求家长和朋友帮助.特别是小组命题过程中，合作就显得至为重要.

其四，做好跟踪扶持.老师对学生命题的试卷考前要全部收缴检查，对有问题的试卷及时给予个别扶持帮助.

其五，做好试卷自主批改的培训工作.辅导学生如何批改试卷，明晰步骤和得分点，协助学生如何给出标准答案，如何建立分步评分标准.

实践证明，学生自主检测是可行的，学生可以认真负责的出好试卷，组织好考试并做好阅卷工作.特别是小组合作命题，普遍都能够出一份很好的试卷.

3.2 反馈反思，促进学生元认知生成

学生自主检测，学生个人及小组的命题情况以及自我批改情况，老师都要跟踪反馈评价.老师评价学生，学生自我评价，学生之间相互评价，小组之间相互评价，都要建立反馈评价机制.情感态度方面，教师要了解学生是认真完成试卷命题，还是应付完成，还是消极抵制，还是变相抄袭，掌握学生对自主命题的情感、态度及价值的认识.命题时间方面，要掌握学生完成命题大约花费多少时间，不能变相加重学生负担.考题来源方面，对试卷中学生比较得意的题目，要追究学生问题的来源，是来自课本？来自复习资料？来自家长朋友帮助？来自培训机构？自己改编？还是自己编拟？等等.了解学生为什么选这个题，是否真正理解了这个问题的奥妙.对学习促进方面，了解自主命题对学习的影响.通过自主命题对自己的学习起到什么作用，能否促进自己梳理知识的系统性，从整体上提升自己的学力，还是没有什么作用白白浪费时间.学生也表示自己出题有趣、考试形式新颖，可以了解到其他学生的学习情况，也可以弥补自己学习的不足，对自己的学习有一定的帮助，特别是让学生自己阅卷，增加了他们的责任心.

“知人者智，自知之明.胜人者有力，自胜者强.”(《道德经》)，通过跟踪评价，促进元认知生成.让学生对自主考试有个自我反思，进一步激发学生的潜能，使潜能转化为现实的学习能力，从而更好地促进学生下阶段的学习.比如，调查显示，学生选择考题的时候，绝大多数学生首先想的是“题目好不好”，而不是我“会不会”.整个自主考试过程学生跳出“分数”的束缚，会非常认真的享受自我评价的过程.再比如，以前的统计发现，12.1%的命题来自课本原题，79.7%来自其它资料的原题，只有8.2%是其它问题稍加改动的题.为此，我们针对性的训练学生如何利用课本问题去拓展、改编问题或者受其启发编拟新问题.现在，这个比例大幅提升，一度达到23.7%.当然，学生拓展、编拟的问题有时很幼稚，但点点滴滴都是学生创新思维的闪现，长期积累在学生思维更加厚重的同时，也使学生的创新思维得到发展.

改变“千人一卷”的考试评价方式，让学生出适合自己的测试卷，既增加学生的学习情感态度和价值观，使学生能更主动地投入以后的学习.又寓考于乐，促进学生元认知能力生成，何乐而不为呢？可以讲，老师对学生的信任换回了学生对老师的信任，也换回了学生对自己的负责，这也是育人.

3.3一纸多卷，“考试内容我做主”

在一些重要节点的考试中，尝试一纸多卷分层检测，学生自主选择自己的考试内容.将试卷分成必做题和选做题两部分，必做题为基础部分，严格按照课程标准注重学生的基本知识、基本技能、基本过程、基本方法的考察，共60分.按照布鲁姆的认知分类，必做题只要达到“领会”层次.选做题分A、B、C三部分，学生只能且必须选择其中的一部分进行测试.这三部分既不同又相互关联，每部分40分.A部分达到“运用”层次，B部分达到“分析”层次，C 部分达到“综合”和“评价”的层次.

统计表明，有大约23%的学生选择A卷，60%选择B卷，17%选择C卷，也符合学生学习状况的正态分布，说明学生对自己还是有较为清醒的自我认知和评价定位.这样，学生根据自己情况各有所需各有发展.A考出自信，B考出灿烂，C考出骄傲，这不正是我们所期盼的吗？

4 结束语

我们常说“授人以鱼，不如授人以渔”.事实上，“授人以渔”首先要“近人以水”.只有近水尝到了鱼的鲜美，才有“临渊羡鱼”之念，进而思索“退而结网”.此时，根本不要老师“授人以渔”了 .通过考试让学生思索如何去自己“结网”，如何才能结好网，这比考出个分数更重要.

在自主命题中发掘学生的潜能，在选择性考试中满足学生的需要.通过自我的选择建立学生的自信，通过对学生自主考试的反思，促进师生元认知的生成，反过来再助推师生发展，这才能超越“考分”，进入育人的范畴，此考之大者！