2017年北京市中考数学学科试题解析

王亮亮

(北京教育考试院 100083)

范永春

(清华大学附属中学 100084)

前言

2017年是北京市全面实施中考考试内容与形式改革的第三年.在《课程标准(2011年版)》和《考试说明(2017)》的引领下，2017年北京市中考数学试题的命制以“核心概念”、“四基”和“四能”为主线，继承、发扬了2015—2016年的命题指导思想(“五个考出来”和“三个注重”)，巩固、发展了2015—2016年的改革成果，通过对数学学科素养的考查，体现了立德树人、育人为本的教育目标和社会发展对人才培养的需求.

1 以学生的课堂学习过程为载体，考查核心概念，将对核心概念的考查与学生的课堂学习过程融为一体，考查学生在解决实际问题的过程中对所学知识、方法的理解与应用，在过程中考查学生对数学思想的感悟与认知

核心概念是数学学科的基石.学生在学习过程中，培养和建立了关于数学的感悟、意识、思想、能力等，并在此基础上，对数学概念、对象和结构以及方法进行了本质性的认识.但对于知识、思想、方法的认知不能停留在理论学习层面上，而是应该使用所学的知识、思想、方法去引导学生的日常学习与生活.

例如，数据分析观念.在统计教学中，教师通过设计有效的统计活动，让学生经历完整的统计过程，包括收集数据、整理数据、展示数据、从数据中提取有效信息，并利用这些信息解决问题.在这一学习过程中，学生不断地建立与培养了统计活动的有关概念、知识与能力，并加深了对统计思想与方法的理解.培养数据分析观念的最终目地应该是为学生提供了一种用“数据”的眼光去看待和对待自己的日常学习与生活的能力，而不是单一的对知识的记忆与模仿.

例1某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整.

收集数据从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩(百分制)如下：

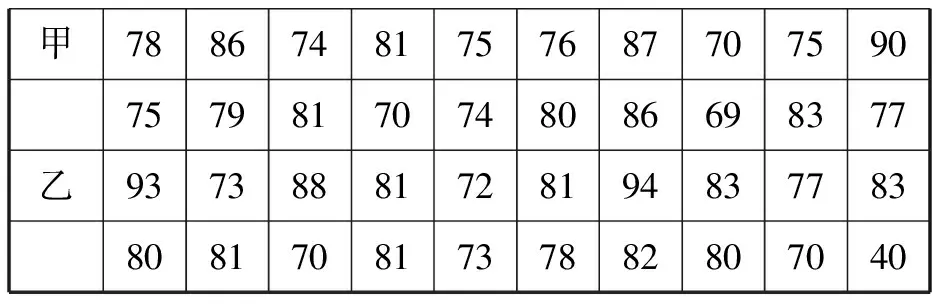
甲7886748175768770759075798170748086698377乙9373888172819483778380817081737882807040

整理、描述数据按如下分数段整理、描述这两组样本数据：

部门人数成绩x40≤x≤4950≤x≤5960≤x≤6970≤x≤7980≤x≤8990≤x≤100甲0011171乙

(说明：成绩80分及以上为生产技能优秀，70～79分为生产技能良好，60～69分为生产技能合格，60分以下为生产技能不合格)

分析数据两组样本数据的平均数、中位数、众数如下表所示：

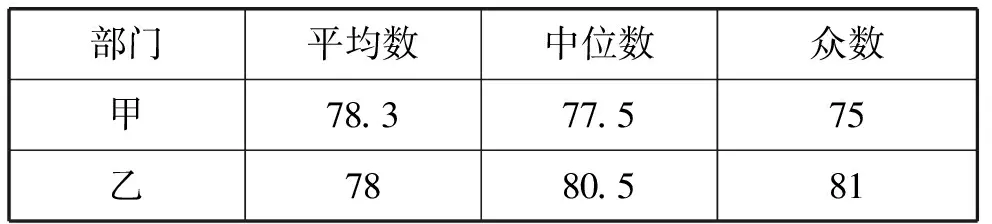
部门平均数中位数众数甲78.377.575乙7880.581

得出结论a．估计乙部门生产技能优秀的员工人数为；

b．可以推断出部门员工的生产技能水平较高，理由为．(至少从两个不同的角度说明推断的合理性)

分析试题的命制思想来源于“人教版”八年级下册第二十章的“课题学习”和“北京版”七年级下册第九章的“综合与实践”.试题以“调查了解某工厂甲、乙两个部门员工的生产技能情况”为载体，呈现了学生进行统计调查的全过程(抽样方法与样本容量的确定、数据的整理与描述、数据的分析、调查结论的分析与得出).

在过程中对学生进行统计考查，使得统计学习的内容不再是单一的聚焦于统计的基础知识，而是聚焦于学生是否了解、理解统计的思想(调查的思想、抽样的思想、随机的思想、定性与定量分析的思想)，聚焦于学生是否具有了统计的思维(非确定性思维).这恰恰是数据分析观念这一核心概念所要求的最本质的内容.

从学生的成长过程来说，统计思维是后续生活学习最重要的思维之一.学生走向社会之后，会遇到各种各样的实际问题，其中“调查类”问题会是学生遇到的最多的实际问题，这种让学生感受获取真实数据的过程，分析调查目的的原因、选取调查的对象、设计调查的问题、应从哪些方面设计调查问题等，都是需要学生具有很好的统计思维，这样学生才能用统计的眼光解决生活中的实际问题.

2 注重对基础知识、基本技能的考查，体现知识之间的关联

2.1 《考试说明(2017)》中指出，注重对基础知识的考查.突出对于支撑学科体系的重点知识的考查，注重知识的整体性和知识之间的内在联系

对于基础知识的考查，不能依赖于死记硬背，而是应以理解为基础，在知识的应用中不断的深化，注重考查知识的形成过程以及知识之间的内在联系.

例2如图，在平面直角坐标系xOy中，△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的，写出一种由△OCD得到△AOB的过程：.

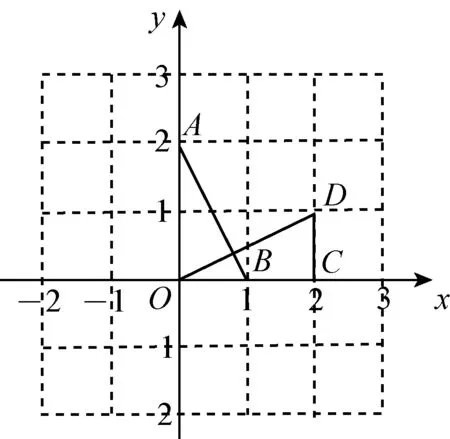
分析试题的呈现不是单纯的把轴对称、旋转、平移的基本性质作为现成的结论呈现给学生，而是将知识放到一个整体的知识体系中——图形的变化.让学生通过图形的运动变化去思考两个图形的变化的过程，让学生去思考轴对称、旋转、平移变化的区别与联系，通过感受图形变化过程中的不变量和不变关系，设计一个运动变化的过程.

2.2 《考试说明(2017)》中指出，注重对基本技能的考查.考查技能操作的程序与步骤以及其中蕴含的原理

例3下面是“作已知直角三角形的外接圆”的尺规作图过程.

已知：Rt△ABC，∠C=90°.

求作：Rt△ABC的外接圆.

作法：如图，

(2)作直线PQ，交AB于点O；

(3)以O为圆心，OA为半径作⊙O.

⊙O即为所求作的圆.

请回答：该尺规作图的依据是.

分析考查的落脚点不是在尺规作图的操作层面，而是落脚于“为什么这么作”、“这么作的原因是什么”，考查的是技能操作里面蕴含的数学原理.

3 注重发现、提出问题能力的考查，与分析、解决问题能力并重，体现“问题”意识

发现问题和提出问题是培养学生创新意识和创新能力的前提，也是对创新人才培养的基本要求.发现、提出问题主要是通过多角度的数学思维，在看似没有关系的问题或多重杂乱关系中找到数量或空间方面的本质联系，使用数学语言、数学符号以“问题”的形式表示出来，通过分析，最终得以解决.

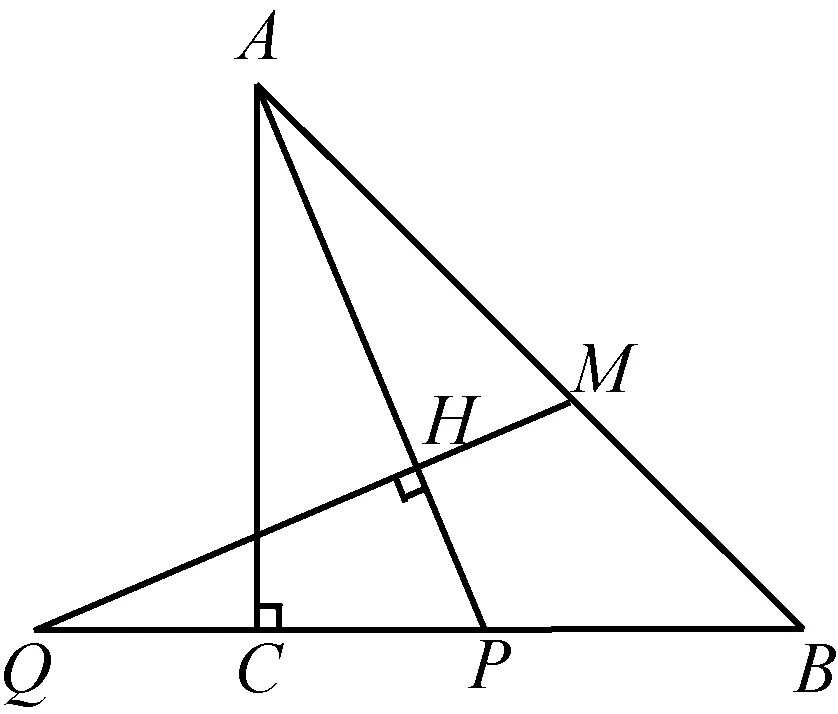
例4在等腰直角△ABC中，∠ACB=90°，P是线段BC上一动点(与点B，C不重合)，连接AP，延长BC至点Q，使得CQ=CP，过点Q作QH⊥AP于点H，交AB于点M.

(1)若∠PAC=α，求∠AMQ的大小(用含α的式子表示)；

(2)用等式表示线段MB与PQ之间的数量关系，并证明.

分析试题的呈现形式是让学生经历分析图形的变化过程，发现线段MB与PQ之间的关系，并将问题解决.这样的过程可以简单的概括为培养学生从数学角度出发的“问题意识”.设置适当的数学情境，让学生用数学的眼光来看待和分析这些情境，引导学生发现问题和提出问题，也引导学生分析问题和解决问题，进而可以体现出对创新意识和创新能力的考查.

4 巩固改革成果，考查基本活动经验，体现知识本质与数学思想

2017年的第26题是对2015、2016年第26题(研究函数的基本过程)的继承与发展.学生根据学习函数所积累的基本活动经验，通过取点、画图、测量得到了函数y随自变量x的变化而变化的数值，通过建立适当的平面直角坐标系画出适当的函数图象，并利用函数图象解决相应的问题.

小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

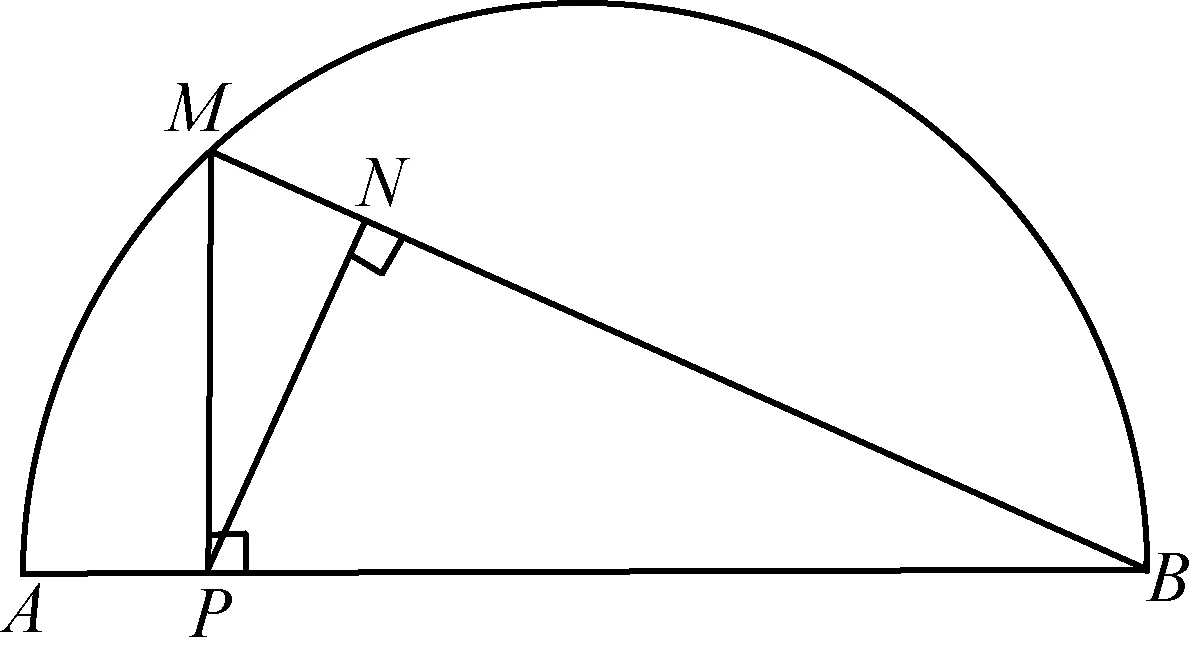
下面是小东的探究过程，请补充完整：

(1)通过取点、画图、测量，得到了x与y的几组值，如下表：

x/cm0123456y/cm02.02.32.10.90

(说明：补全表格时相关数值保留一位小数)

(2)建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

(3)结合画出的函数图象，解决问题：当△PAN为等腰三角形时，AP的长度约为cm.

分析函数是研究实际问题的重要数学模型，它来源于实际又服务于实际，从实际中抽象出函数的有关概念，又运用函数解决实际问题，这就是试题立意的核心出发点.在建立和运用函数模型的过程中，变化与对应的思想是重要的基础，这也是函数学习过程中需要揭示的最为本质的思想.

5 通过试题反拨教学，实现考试与教学的良性互动

试题设计的思想来源于《课程标准(2011年版)》的例40.试题设置的出发点是体会概率与频率的关系，而不仅仅只关注计算一些事件发生的概率.在概率教学过程中，比较偏向于利用古典概型计算某一随机事件发生的概率，这可能会让学生体会不到随机思想，仍然用确定性思维理解问题.

例6下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断：

①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；

②随着试验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；

③若再次用计算机模拟此实验，则当投掷次数为1000时，“钉尖向上”的频率一定是0.620.

其中合理的是

(A)① (B)② (C)①② (D)①③

分析随机现象表面上看无规律可循，出现哪一个结果事先无法预料，但当我们大量重复试验时，试验的每一个结果都会呈现出其频率的稳定性.试题的设置是让学生体会试验结果的不确定性，感悟随机事件的不确定性思维，引导在教学过程中，经历试验的过程，收集试验数据，分析试验结果，将所得到的结果与自己的猜测进行比较，最后进行理性的分析，体会频率与概率之间的联系与区别.

6 以吴文俊院士在研究中国古代数学的成就为载体，弘扬中华民族传统优秀文化，展现我国伟大数学成就

例7数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等(如图所示)”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证.

(以上材料来源于《古证复原的原则》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)

请根据上图完成这个推论的证明过程.

证明：S矩形NFGD=S△ADC-(S△ANF+S△FGC)，S矩形EBMF=S△ABC-(+).

易知，S△ADC=S△ABC，=，=.

可得S矩形NFGD=S矩形EBMF.

分析试题通过介绍我国数学家吴文俊院士的数学成就，让学生了解我国古现代数学的发展，并通过阅读，提取有效信息完善数学成就主要原理的步骤.这一过程不仅将学生所学的知识的来源进行了介绍，更重要的是让学生感受我国古代数学家和现代数学家对我国数学发展所作出的伟大成就.

7 以“一带一路”沿线经济发展数据为载体，既介绍了“一带一路”的发展情况，又考查了学生读取、分析数据的能力

例8下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.

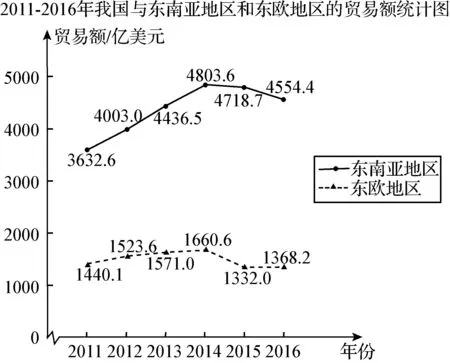
(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)

根据统计图提供的信息，下列推断不合理的是

(A)与2015年相比，2016年我国与东欧地区的贸易额有所增长

(B)2011-2016年，我国与东南亚地区的贸易额逐年增长

(C)2011-2016年，我国与东南亚地区的贸易额的平均值超过4200亿美元

(D)2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多

分析“一带一路”是我国经济发展新的引擎，以“一带一路”经济发展情况为载体，既让学生了解了我国的综合国力，又考查了学生对于数据的分析能力.