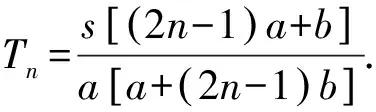一道教师解题大赛试题的解答与推广
陆信明
(湖南省常德市第三中学 415000)
2016年11月,笔者参加了湖南省第二届数学教师解题大赛,遇到了这样一道有趣的试题.
题目8位乘客乘坐两辆小汽车从山区赶往火车站乘车,可是不巧,其中一辆汽车在距离火车站20千米的地方出了故障,不能行驶,此时离火车站停止检票上车的时间只剩下52分钟.这时唯一可以乘坐的交通工具只有一辆小汽车连同司机在内一次限乘5人,小汽车的平均速度为60千米/小时,乘客步行的平均速度为6千米/小时.
(1)如果小汽车送第一批乘客的同时,第二批乘客先步行,小汽车把第一批乘客送到火车站后立即返回接送在步行中的第二批乘客,这8乘客是否能全部赶上火车(忽略上下车时间)?
(2)是否还有比(1)更省时的方案(不改变人和车的速度)?若有,请你设计更省时的方案,并求出该方案所需的时间;若没有,请说明理由.
下文对这道试题作一些研究,首先给出这个问题的解答,然后作一般性的推广.
1 原问题的解答
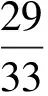
(2)先求出最省时的方案:

则汽车从相遇点送第二批乘客到终点的时间为
以下分两种情况讨论:
(1)当第二批乘客到终点时,第一批乘客已到终点或恰好到终点,则有
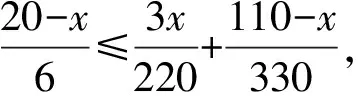
两批乘客到站所需的总时间为

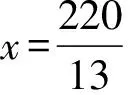
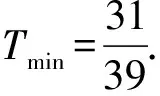
(2)当第二批乘客到终点时,第一批乘客未到终点,则有
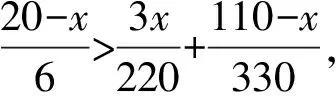
在该情况下,汽车还需再去接送第一批乘客.
在(t2+t3)时间段,第一乘客已走的路程为
汽车从终点返程与第一批乘客相遇的时间为
汽车从相遇点送第一批乘客到终点还需的时间为
两批乘客到站所需的总时间为
T=t1+t2+t3+t4+t5
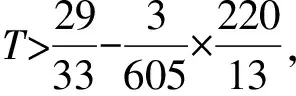
综上,
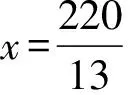
2 问题的推广
推广1通过上述解法,我们可以发现,当两批乘客同时到站时,所用的总时间最短.也就是说,若有一批乘客先到站,到站后速度变为0,不能为人和车这套系统贡献速度,时间将会变长.不禁思考,对于一般的情况:汽车与两批乘客距离终点s千米,汽车速度为a千米/时,乘客步行速度为b千米/时,且a>b,汽车接送乘客到站的最短时间是多少呢?
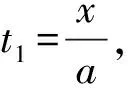
汽车送完第一批乘客后与第二批乘客相遇的时间为
此时相遇点与终点的距离为
则汽车从相遇点送第二批乘客到终点的时间为
由前面的分析可知,当两批乘客同时到站时,所需的总时间最短,而第一批乘客步行到站的时间为
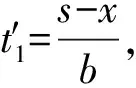
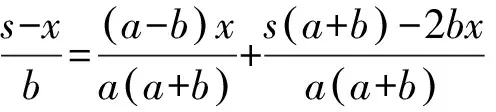

两批乘客到站所需的总时间为
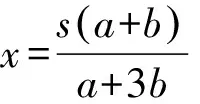
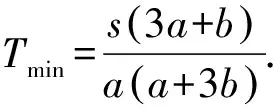
推广2若把推广1中的两批乘客变为三批(其余条件不变),那么,汽车接送三批乘客所需的最短时间呢?
解通过前面的分析我们可以发现当三批乘客同时到站时,所用的总时间最短.
我们把第二、三批看成一个整体,由前面的解答有
汽车送完第一批乘客后与第二、三批乘客相遇的时间为
相遇点与终点的距离为

由推广1中的结论可知,第二、三批乘客到站所需的最短时间为
且第二、三批乘客到站时第一批乘客也刚好到站所需的总时间最短,
即t1′=t2+t,
三批乘客到站所需的总时间为
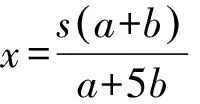
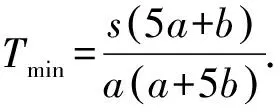
一般性推广对于更一般的问题:一辆汽车送n批乘客到距离s千米的车站,汽车速度为a千米/时,乘客步行速度为b千米/时,且a>b,汽车接送乘客到站的最短时间是多少呢?
解设一辆汽车送n批乘客到站的最短时间为Tn,汽车送第一批乘客的路程为xn,则有
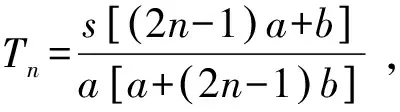
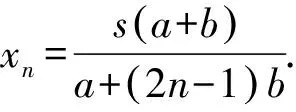
下面用数学归纳法证明.
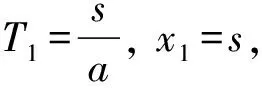
即一批乘客直接乘车到站,符合题意.
假设当n=k(k≥2)时,
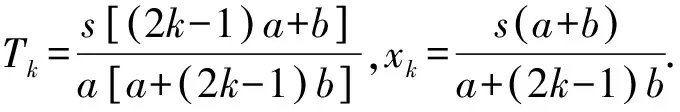
当n=k+1时,把后k批乘客看成一个整体,
汽车送完第一批乘客后与后k批乘客相遇的时间为
相遇点与终点的距离为

①
由假设可知,后k批乘客到站所需的最短时间为
且后k批乘客到站时第一批乘客也刚好到站所需的总时间最短,即
把①代入有
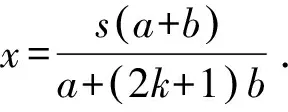
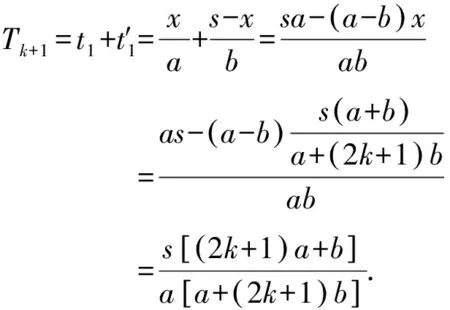
综上,命题得证.